Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 93

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 10.
Объясни, как можно узнать:
1) один из двух множителей, если известны произведение и другой множитель;
2) делимое, если известны делитель и частное;
3) делитель, если известны делимое и частное.
1) Если известны произведение и другой множитель, то чтобы найти другой множитель, нужно произведение разделить на другой множитель.
х ∙ а = m
x = m : а
2) Если известны делитель и частное, то, чтобы найти делимое, нужно делитель умножить на частное.
х : а = m
х = а ∙ m
3) Если известны делимое и частное, то, чтобы найти делитель нужно делимое разделить на частное.
а : х = m
х = а : m
Повтори, как называются числа при делении.
Рассуждаем.
1) Если известны произведение и другой множитель, то чтобы найти другой множитель, нужно произведение разделить на другой множитель.
х ∙ а = m
x = m : а
2) Если известны делитель и частное, то, чтобы найти делимое, нужно делитель умножить на частное.
х : а = m
х = а ∙ m
3) Если известны делимое и частное, то, чтобы найти делитель нужно делимое разделить на частное.
а : х = m
х = а : m
Оформляем задание в тетрадь .
Номер 11.
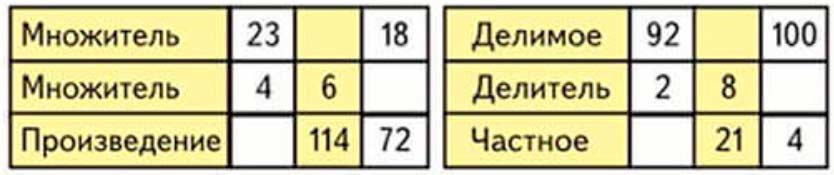
Заполни таблицы.


1 множитель ∙ 2 множитель = произведение
1 множитель = произведение : 2 множитель
2 множитель = произведение : 1 множитель
23 ∙ 4 = 92, нужно найти произведение, зная множители.
114 : 6 = 19, нужно найти множитель, зная произведение и другой множитель.
72 : 18 = 4, нужно найти множитель, зная произведение и другой множитель.
Делимое : делитель = частное
Делимое = делитель ∙ частное
Делитель = делимое : частное
92 : 2 = 46, нужно найти частное, зная делимое и делитель.
8 ∙ 21 = 168, нужно найти делимое, зная делитель и частное.
100 : 4 = 25, нужно найти делитель, зная делимое и частное.
Повтори, как называются числа при умножении и делении.
Рассуждаем и выполняем вычисления.
1 множитель ∙ 2 множитель = произведение
1 множитель = произведение : 2 множитель
2 множитель = произведение : 1 множитель
23 ∙ 4 = 92, нужно найти произведение, зная множители.
114 : 6 = 19, нужно найти множитель, зная произведение и другой множитель.
72 : 18 = 4, нужно найти множитель, зная произведение и другой множитель.
Делимое : делитель = частное
Делимое = делитель ∙ частное
Делитель = делимое : частное
92 : 2 = 46, нужно найти частное, зная делимое и делитель.
8 ∙ 21 = 168, нужно найти делимое, зная делитель и частное.
100 : 4 = 25, нужно найти делитель, зная делимое и частное.
Заполняем таблицы.
Номер 12.
Реши следующие уравнения.
Ответ:
х ∙ 19 = 76
х - неизвестный множитель
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
х = 76 : 19
х = 4
Ответ: 4.
32 ∙ х = 128
х - неизвестный множитель
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
х = 128 : 32
х = 4
Ответ: 4.
560 : х = 8
х - неизвестный делитель
Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
х = 560 : 8
х = 70
Ответ: 70.
х : 14 = 6
х - неизвестное делимое
Чтобы найти неизвестное делимое, нужно делитель умножить на частное.
х = 6 ∙ 14
х = 84
Ответ: 84.
Повтори, как решать уравнения.
Выполняем вычисления.
х ∙ 19 = 76
х – неизвестный множитель
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
х = 76 : 19
х = 4
Ответ: 4.
32 ∙ х = 128
х – неизвестный множитель
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
х = 128 : 32
х = 4
Ответ: 4.
560 : х = 8
х – неизвестный делитель
Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
х = 560 : 8
х = 70
Ответ: 70.
х : 14 = 6
х – неизвестное делимое
Чтобы найти неизвестное делимое, нужно делитель умножить на частное.
х = 6 ∙ 14
х = 84
Ответ: 84.
Оформляем задание в тетрадь.
Номер 13.
Объясни, что означают записи на полях, и реши уравнения.

Ответ:
0 ∙ х = 0
При умножении нуля на любое число, получается ноль.
b ∙ 0 = 0
Если любое число умножить на ноль, то получается ноль.
0 : с = 0
При делении нуля на любое число получается ноль.
х ∙ 57 = 0
Мы видим, что при умножении х на 57 получается ноль. Такое возможно, когда ноль умножают на любое число, значит х равно нулю.
х = 0 : 57
х = 0
Ответ: 0.
789 ∙ х = 0
Мы видим, что при умножении 789 на х получается нуль. Такое возможно, когда любое число умножают на нуль, значит х равно нулю.
х = 0 : 789
х = 0
Ответ: 0.
12 : х = 12
Мы видим, что при делении 12 на х получается 12. Такое возможно, когда число делят на единицу.
х = 12 : 12
х = 1
Ответ: 1.
х : 697 = 0
Мы видим, что при делении х на 697 получается нуль. Такое возможно при делении нуля на любое число.
х = 697 ∙ 0
х = 0
Ответ: 0.
х ∙ 14 = 14
Мы видим, что при умножении х на 14 получается 14. Такое возможно при умножении числа на единицу.
х = 14 : 14
х = 1
Ответ: 1.
45 : х = 1
Мы видим, что при делении 45 на х получается 1. Такое возможно при делении числа на себя.
х = 45 : 1
х = 45
Ответ: 45.
Повтори, как решать уравнения, а также как называются числа при умножении и делении.
Объясним, что означают записи на полях.
0 ∙ х = 0
При умножении нуля на любое число, получается нуль.
b ∙ 0 = 0
Если любое число умножить на нуль, то получается нуль.
0 : с = 0
При делении нуля на любое число получается нуль.
Решим уравнения.
х ∙ 57 = 0
Мы видим, что при умножении х на 57 получается нуль. Такое возможно, когда нуль умножают на любое число, значит х равно нулю.
х = 0 : 57
х = 0
Ответ: 0.
789 ∙ х = 0
Мы видим, что при умножении 789 на х получается нуль. Такое возможно, когда любое число умножают на нуль, значит х равно нулю.
х = 0 : 789
х = 0
Ответ: 0.
12 : х = 12
Мы видим, что при делении 12 на х получается 12. Такое возможно, когда число делят на единицу.
х = 12 : 12
х = 1
Ответ: 1.
х : 697 = 0
Мы видим, что при делении х на 697 получается нуль. Такое возможно при делении нуля на любое число.
х = 697 ∙ 0
х = 0
Ответ: 0.
х ∙ 14 = 14
Мы видим, что при умножении х на 14 получается 14. Такое возможно при умножении числа на единицу.
х = 14 : 14
х = 1
Ответ: 1.
45 : х = 1
Мы видим, что при делении 45 на х получается 1. Такое возможно при делении числа на себя.
х = 45 : 1
х = 45
Ответ: 45.
Оформим задание в тетрадь.
Номер 14.
Вычисли значения выражений.
Ответ:
278 ∙ 0 = 0
278 ∙ 1 = 278
0 : 47 = 0
94 : 1 = 94
75 ∙ 4 ∙ 0 ∙ 3 = 0
36 ∙ (63 − 63) ∙ 10 = 0
Повтори свойства умножения и деления.
Выполняем вычисления по действиям.
278 ∙ 0 = 0
278 ∙ 1 = 278
0 : 47 = 0
94 : 1 = 94
75 ∙ 4 ∙ 0 ∙ 3 = 0
1) 75 ∙ 4 = 300
2) 300 ∙ 0 = 0
3) 0 ∙ 3 = 0
36 ∙ (63 - 63) ∙ 10 = 0
1) 63 – 63 = 0
2) 36 ∙ 0 = 0
3) 0 ∙ 10 = 0
Оформляем задание в тетрадь.
278 ∙ 0 = 0
278 ∙ 1 = 278
0 : 47 = 0
94 : 1 = 94
75 ∙ 4 ∙ 0 ∙ 3 = 0
36 ∙ (63 − 63) ∙ 10 = 0
Номер 15.
Какие свойства умножения ты знаешь (с. 120)? Объясни, почему верны следующие равенства:
Ответ:
Свойства умножения:
1) от перестановки множителей произведение не меняется;
2) два соседних множителя можно заменить их произведением.
Равенство 12 ∙ 35 = 35 ∙ 12 верно на основании переместительного свойства умножения: от перестановки множителей произведение не изменяется.
Равенство 17 ∙ 5 ∙ 2 = 17 ∙ 10 верно на основании того, что два соседних множителя можно заменить их произведением.
Повтори свойства умножения.
Вспомним свойства умножения.
Свойства умножения:
1) от перестановки множителей произведение не меняется;
2) два соседних множителя можно заменить их произведением.
Объясним, почему верны данные равенства.
Равенство 12 ∙ 35 = 35 ∙ 12 верно на основании переместительного свойства умножения: от перестановки множителей произведение не изменяется.
Равенство 17 ∙ 5 ∙ 2 = 17 ∙ 10 верно на основании того, что два соседних множителя можно заменить их произведением.
Номер 16.
Покажи на примерах, как можно умножить сумму нескольких чисел на какое-либо число; как можно разделить сумму на число.
Ответ:(4 + 3) ∙ 2 = 4 ∙ 2 + 3 ∙ 2 = 8 + 6 = 14 или (4 + 3) ∙ 2 = 7 ∙ 2 = 14 (20 + 15) : 5 = 20 : 5 + 15 : 5 = 4 + 3 = 7 или (20 + 15) : 5 = 35 : 5 = 7
Повтори свойства умножения и деления.
Рассуждаем.
При умножении суммы на число можно умножить на него каждое слагаемое в отдельности и полученные результаты сложить.
Чтобы разделить сумму на число, можно сначала вычислить значение суммы и полученный результат разделить.
Чтобы разделить суммы на какое-нибудь число, можно разделить на это число каждое слагаемое отдельно и полученные частные сложить.
Приведем примеры.
(4 + 3) ∙ 2 = 4 ∙ 2 + 3 ∙ 2 = 8 + 6 = 14 или (4 + 3) ∙ 2 = 7 ∙ 2 = 14
(20 + 15) : 5 = 20 : 5 + 15 : 5 = 4 + 3 = 7 или (20 + 15) : 5 = 35 : 5 = 7
Номер 17.
Выполни вычисления и проверь их.
Ответ:
Повтори алгоритм письменного умножения и деления многозначных чисел.
Выполним вычисления с проверкой.
Пишу: 4 078 ∙ 6.
Умножаю единицы: 8 ∙ 6 = 48. 48 ед. – это 4 дес. и 8 ед., 8 ед. пишу под единицами, а 4 дес. запомню и прибавлю к десяткам после умножения десятков.
Умножаю десятки: 7 ∙ 6 = 42. К 42 дес. прибавляю 4 дес., которые получены при умножении единиц: 42 + 4 = 46. 46 дес. – это 4 сот. и 6 дес., 6 дес. пишу под десятками, а 4 сот. запомню и прибавлю к сотням после умножения сотен.
Умножаю сотни: 0 ∙ 6 = 0. К 0 сот. прибавляю 4 сот., которые получены при умножении десятков: 0 + 4 = 4. Пишу 4 сот. под сотнями.
Умножаю единицы тысяч: 4 ∙ 6 = 24. 24 ед. тыс. – это 2 дес. тыс. и 4 ед. тыс.; 4 ед. тыс. пишу под единицами тысяч, а 2 дес. тыс. запишу под десятками тысяч, так как других десятков тысяч для умножения нет.
Читаю ответ: 24 468.
Чтобы проверить умножение, можно произведение разделить на один из множителей и в результате деления должен получиться другой множитель.
Пишу: 51 200 : 80.
Разделю 51 200 на 80. Выделю первое неполное делимое – 512. Разделю 51 на 8, получу 6 – это пробная цифра.
Проверяю, подходит ли цифра 8.
Умножу 80 на 6, получу 480.
512 – 480 = 32 сот. Добавляю 0 дес.
Нахожу вторую цифру частного:
320 : 80, получу 4.
Умножу 80 на 4, получу 320.
320 – 320 = 0.
Нахожу третью цифру частного:
0 : 80 = 0.
Частное – 640.
Чтобы проверить деление, можно частное умножить на делитель и в результате умножения должно получится делимое.
Далее рассуждаю аналогично.
Продолжаем выполнять вычисления и оформляем задание в тетрадь.

Номер 18.
Выполни деление с остатком и сделай проверку.
Ответ:
Повтори, как выполнять деление с остатком.
Вспомним как выполнять проверку.
Проверка:
1) Остаток должен быть меньше делителя.
2) Умножим частное на делитель.
3) Прибавим к результату остаток. Сумма должна быть равна делимому.
Выполним вычисления с проверкой и оформим задание в тетрадь.
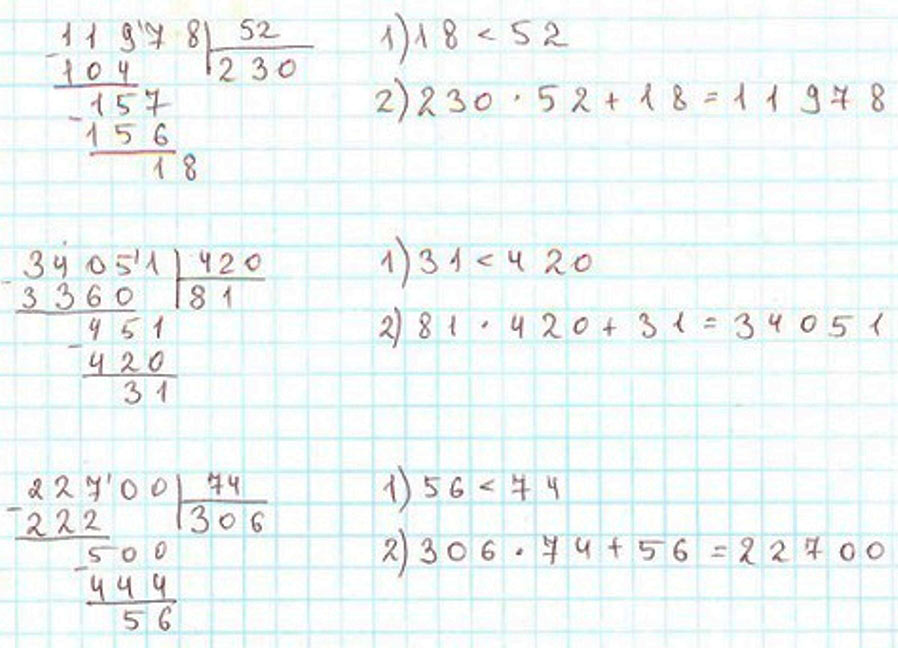
Номер 19.
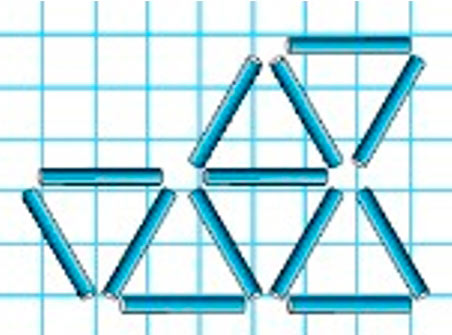
Выложи такую фигуру из палочек. Убери 3 палочки так, чтобы осталось 3 треугольника.

Ответ:

Повтори, какие бывают треугольники.
Выложим из палочек фигуру как на полях.
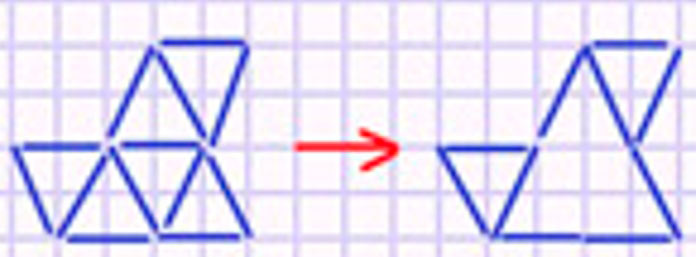
Уберем три палочки и посмотрим, что получится.
Выражения и уравнения
Номер 8.
Объясни, как можно узнать:
1) одно из двух слагаемых, если известны сумма и другое слагаемое;
2) уменьшаемое, если известны разность и вычитаемое;
3) вычитаемое, если известны уменьшаемое и разность.
1) Если известна сумма и другое слагаемое, то, чтобы найти одно из слагаемых, нужно из суммы вычесть другое слагаемое. Например: х + 17 = 34 х = 34 − 17 х = 17 2) Чтобы найти неизвестное уменьшаемое, зная разность и вычитаемое, нужно к разности прибавить вычитаемое. Например, х − 13 = 10 х = 10 + 13 х = 23 3) Чтобы найти неизвестное вычитаемое, зная уменьшаемое и разность, нужно от уменьшаемого отнять разность. Например, 33 − х = 30 х = 33 − 30 х = 3
Номер 9.
Заполни таблицы.


1 слагаемое + 2 слагаемое = сумма
1 слагаемое = сумма − 2 слагаемое
2 слагаемое = сумма − 1 слагаемое
31 − 25 = 6 (нужно найти неизвестное слагаемое, зная сумму и другое слагаемое)
20 − 12 = 8 (нужно найти неизвестное слагаемое, зная сумму и другое слагаемое)
95 − 70 = 25 (нужно найти неизвестное слагаемое, зная сумму и другое слагаемое)
Уменьшаемое − вычитаемое = разность
Вычитаемое = уменьшаемое − разность
Уменьшаемое = вычитаемое + разность
80 − 5 = 75 (нужно найти неизвестное вычитаемое, зная уменьшаемое и разность)
17 + 3 = 20 (нужно найти неизвестное уменьшаемое, зная вычитаемое и разность)
25 − 10 = 15 (нужно найти неизвестное вычитаемое, зная уменьшаемое и разность)
Номер 10.
Реши уравнения.
Ответ:
х − 59 = 76
х − неизвестное уменьшаемое
Чтобы найти неизвестное, нужно к вычитаемому прибавить разность.
х = 76 + 59
х = 135
Ответ: 135.
84 − х = 43
х − неизвестное вычитаемое
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
х = 84 − 43
х = 41
Ответ: 41.
х + 48 = 95
х − неизвестное слагаемое
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть другое слагаемое.
х = 95 − 48
х = 47
Ответ: 47.
34 + х = 82
х − неизвестное слагаемое
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть другое слагаемое.
х = 82 − 34
х = 48
Ответ: 48.
Номер 11.
Объясни, что означают записи на полях, и реши уравнения.
Ответ:
а + 0 = а
Если к числу прибавить нуль, то получается это же число.
0 + а = а
Если к нулю прибавить число, то значение суммы будет равно данному числу.
с − 0 = с
Если из числа вычесть нуль, то получится это же число.
b − b = 0
Если из числа вычесть само себя, то получится нуль.
156 − х = 156
При вычитании из 156 х получилось 156, то есть при вычитании из числа получилось это же число, а такое происходит, когда вычитаемое равно нулю.
х = 156 − 156
х = 0
Ответ: 0.
х + 267 = 267
Мы видим, что к х прибавляется число 267, а значение суммы равно 267. Такое возможно при прибавлении числа к нулю.
х = 267 − 267
х = 0
Ответ: 0.
987 + х = 987
Мы видим, что к 987 прибавляется х, а значение суммы равно 987, то есть первому слагаемому. Такое возможно при прибавлении числа к нулю.
х = 987 − 987
х = 0
Ответ: 0.
х − 17 = 0
Мы видим, что при вычитании из х 17 получается нуль. Такое возможно, когда уменьшаемое и вычитаемое равны.
х = 17 + 0
х = 17
Ответ: 17.
Номер 12.
Найди значения выражений.
Ответ:
1970 + 0 = 1970
1970 − 0 = 1970
239 + (437 − 437) = 239 + 0 = 239
365 − (260 + 105) = 365 − 365 = 0
560 − (260 + 300) + 99 = 560 − 560 + 99 = 0 + 99 = 99
(87 − 87) + (78 − 78) = 0 + 0 = 0
Номер 13.
Чему равна сумма двух слагаемых, если одно из них равно нулю? Чему равна разность, если вычитаемое равно нулю?
Ответ:Если одно из слагаемых равно нулю, то их сумма равна другому слагаемому. а + 0 = а Если вычитаемое равно нулю, то разность равна уменьшаемому. с − 0 = с
Номер 14.
Приведи примеры, когда сумма двух слагаемых равна одному из них; когда разность равна уменьшаемому; когда разность равна нулю.
Ответ:Сумма двух слагаемых равна одному из слагаемых, когда другое равно нулю. Например: 7 + 0 = 7; 51 + 0 = 51; 46 + 0 = 46. Разность равна уменьшаемому в том случае, когда вычитаемое равно нулю. Например: 65 − 0 = 65; 77 − 0 = 77; 1 − 0 = 1. Разность равна нулю в том случае, когда уменьшаемое и вычитаемое равны. Например: 67 − 67 = 0; 45 − 45 = 0.
Номер 15.
Какие свойства сложения ты знаешь (с. 118)? Объясни, почему верны следующие равенства:
16 + 75 = 75 + 16
8 + 17 + 3 = 8 + 20
1) От перестановки слагаемых сумма не меняется. 2) Два соседних слагаемых можно заменить их суммой. Равенство 16 + 75 = 75 + 16 верно на основании переместительного свойства сложения. Равенство 8 + 17 + 3 = 8 + 20 верно на основании того, что два соседних слагаемых можно заменять их суммой.
Номер 16.
Используя и перестановку, и группировку слагаемых, числа можно складывать в любом порядке. Объясни, как можно легче выполнить сложение.
Ответ:54 + 18 + 26 + 2 = (54 + 26) + (18 + 2) = 80 + 20 = 100 27 + 16 + 13 + 7 + 3 + 14 = (27 + 3) + (16 + 14) + (13 + 7) = 30 + 30 + 20 = 80
Задание на полях страницы
Магический квадрат.


250 + 300 + 50 = 300 + 300 = 600
0 + 200 + 400 = 200 + 400 = 600
350 + 100 + 150 = 100 + 500 = 600
250 + 0 + 350 = 0 + 600 = 600
300 + 200 + 100 = 300 + 300 = 600
50 + 400 + 150 = 200 + 400 = 600
250 + 200 + 150 = 200 + 400 = 600
350 + 200 + 50 = 400 + 200 = 600
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.