Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 92
- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
.jpg "Математика 4 класс Моро, Волкова - 2 часть страница 92")
Номер 1.
В каком случае сложение можно заменить умножением? Покажи на примерах.
Ответ:Умножение - более удобный способ нахождения суммы, состоящей из одинаковых слагаемых и повторяющихся несколько раз. Например: 5 + 5 + 5 = 5 ∙ 3 – можно заменить сложение умножением, а вот 4 + 4 + 4 + 2 – нельзя заменить, потому что сложение не состоит из одного вида слагаемого.
Повтори, как называются числа при сложении.
Рассуждаем.
Умножение – более удобный способ нахождения суммы, состоящей из одинаковых слагаемых и повторяющихся несколько раз.
Приведем пример.
Например:
5 + 5 + 5 = 5 ∙ 3 – можно заменить сложение умножением, а вот 4 + 4 + 4 + 2 – нельзя заменить, потому что сложение не состоит из одного вида слагаемого.
Оформим задание в тетрадь.
Номер 2.
Какими знаками обозначаются умножение и деление и как называются выражения, в которых числа соединены знаком умножения? знаком деления?
Ответ:Умножение обозначается знаком умножить “умножить” (∙). Деление обозначается знаком “разделить” (:). Выражения, в которых числа соединены знаком умножения, называются произведением. Выражения, в которых числа соединены знаком деления, называются частным.
Повтори, как называются числа при умножении и делении.
Рассуждаем.
Умножение обозначается знаком умножить “умножить” (∙).
Деление обозначается знаком “разделить” (:).
Выражения, в которых числа соединены знаком умножения, называются произведением.
Выражения, в которых числа соединены знаком деления, называются частным.
Оформляем задание в тетрадь.
Номер 3.
Покажи, как умножение можно заменить сложением.
Ответ:7 ∙ 3 = 7 + 7 + 7 38 ∙ 4 = 38 + 38 + 38 + 38 156 ∙ 2 = 156 + 156 9 ∙ 6 = 9 + 9 + 9 + 9 + 9 + 9
Повтори, как называются числа при сложении и умножении.
Заменяем умножение сложением.
Умножение можно заменить суммой одинаковых слагаемых.
7 ∙ 3 = 7 + 7 + 7
38 ∙ 4 = 38 + 38 + 38 + 38
156 ∙ 2 = 156 + 156
9 ∙ 6 = 9 + 9 + 9 + 9 + 9 + 9
Оформляем задание в тетрадь.
Номер 4.
Вставь знак >, < или = так, чтобы получилось верное равенство или неравенство.
Ответ:
37 ∙ 4 + 5 < 37 ∙ 5
Слева число 37 умножается на 4, значит это замена сложению 37 + 37 + 37 + 37.
Справа такое сложение выполняют 5 раз, то есть 37 + 37 + 37 + 37 + 37.
Слева прибавляется еще 5. Получается и слева и справа 5 слагаемых, но слева 5, а справа пятым является 37. 5 < 37, значит сумма слева меньше суммы справа.
68 ∙ 7 < 68 ∙ 7 + 68
Слева 68 ∙ 7 заменяет сумму, состоящую из 7 слагаемых каждое из которых равно 68, а справа сумма состоит из 8 слагаемых тоже равных 68.
Значение выражения слева меньше, чем значение выражения справа, так как справа большее число повторение слагаемых.
7 ∙ 9 = 7 ∙ 10 − 7
Слева 7 повторяют в сложении 9 раз и справа тоже, ведь выражение 7 ∙ 10 − 7 можно заменить выражением 7 ∙ 10 − 7 ∙ 1, а это равно 7 ∙ 9.
Повтори, что такое равенство и неравенство.
Рассуждаем и выполняем вычисления.
37 ∙ 4 + 5 < 37 ∙ 5
Слева число 37 умножается на 4, значит это замена сложению 37 + 37 + 37 + 37.
Справа такое сложение выполняют 5 раз, то есть 37 + 37 + 37 + 37 + 37.
Слева прибавляется еще 5. Получается и слева и справа 5 слагаемых, но слева 5, а справа пятым является 37. 5 < 37, значит сумма слева меньше суммы справа.
68 ∙ 7 < 68 ∙ 7 + 68
Слева 68 ∙ 7 заменяет сумму, состоящую из 7 слагаемых каждое из которых равно 68, а справа сумма состоит из 8 слагаемых тоже равных 68.
Значение выражения слева меньше, чем значение выражения справа, так как справа большее число повторение слагаемых.
7 ∙ 9 = 7 ∙ 10 − 7
Слева 7 повторяют в сложении 9 раз и справа тоже, ведь выражение 7 ∙ 10 − 7 можно заменить выражением 7 ∙ 10 − 7 ∙ 1, а это равно 7 ∙ 9.
Оформляем задание в тетрадь.
37 ∙ 4 + 5 < 37 ∙ 5
68 ∙ 7 < 68 ∙ 7 + 68
7 ∙ 9 = 7 ∙ 10 – 7
Номер 5.
Как называются при умножении и делении данные числа и число, которое получается в результате выполнения действия?
Ответ:
При умножении числа, которые умножаем называются первый множитель и второй множитель, а результат умножения − произведение.
Первый множитель ∙ второй множитель = произведение.
При делении число, которое делят, называется делимое, число, на которое делят − делитель, а результат − частное.
Делимое : делитель = частное.
Повтори, как называются числа при умножении и делении.
Рассуждаем .
При умножении числа, которые умножаем называются первый множитель и второй множитель, а результат умножения − произведение.
Первый множитель ∙ второй множитель = произведение.
При делении число, которое делят, называется делимое, число, на которое делят − делитель, а результат − частное.
Делимое : делитель = частное.
Оформляем задание в тетрадь.
8 (первый множитель) ∙ 5 (второй множитель) = 40 (произведение)
40 (делимое) : 8 (делитель) = 5 (частное)
Номер 6.
Прочитай, используя различные словесные формулировки, следующие равенства:
Ответ:
18 ∙ 3 = 54
1) Произведение 18 и 3 равно 54.
2) 18 умножить на 3 равно 54.
3) Если 18 умножить на 3, то получится 54.
4) Первый множитель 18, второй множитель 3, произведение 54.
128 : 4 = 32
1) 128 разделить на 4 равно 54.
2) Частное 128 и 4 равно 32.
3) Делимое 128, делитель 4, частное 32.
4) Если 128 разделить на 4, то получится 32.
Повтори, как называются числа при умножении и делении, а также что такое равенства.
Читаем первое равенство.
18 ∙ 3 = 54
1) Произведение 18 и 3 равно 54.
2) 18 умножить на 3 равно 54.
3) Если 18 умножить на 3, то получится 54.
4) Первый множитель 18, второй множитель 3, произведение 54.
Читаем второе равенство.
128 : 4 = 32
1) 128 разделить на 4 равно 54.
2) Частное 128 и 4 равно 32.
3) Делимое 128, делитель 4, частное 32.
4) Если 128 разделить на 4, то получится 32.
Номер 7.
Составь и реши задачи на умножение и деление, используя слова: «Купили ... вещей по цене ... р.», «Сколько раз по ... содержится в ...?», «Сколько получится в каждой части, если ... разделить на ... равных частей?», «... больше в ... раз», «... меньше в ... раз», «Во сколько раз ... больше, чем ...?», «... в ... раз меньше, чем ...».
Ответ:
Задача 1:
Купили 5 альбомов по цене 25 р. Узнай стоимость покупки.
5 альбомов за ? р.
1 альбом – 25 р.
25 ∙ 5 = 125 (р.) – потратили на всю покупку.
Ответ: 125 рублей всего потратили на всю покупку.
Задача 2:
В бочке 300 л воды, а в ведре 10 л. Сколько раз по 10 л содержится в 300 л?
В бочке – 300 л
В ведре – 10 л
? раз по 10 л в 300 л
300 : 10 = 30 (раз) – в 300 л содержится по 10 л.
Ответ: 30 раз в 300 л содержится по 10 л.
Задача 3:
Длина тесьмы 56 см. Сколько см получится в каждой части, если отрезок разделить на 7 одинаковых частей?
Длина всего – 56 см
Длина 1 части – ? см = 7 кусков
56 : 7 = 8 (см) – длина каждого куска, который получился при делении отрезка в 56 см на 7 кусков.
Ответ:длина каждого из семи кусков составит 8 см.
Задача 4:
Велосипедист проехал 12 км. Ему осталось еще проехать в 2 раза больше. Сколько км велосипедист должен еще проехать?
.jpg "Изображение математика 4 класс Моро, Бантова - 2 часть страница 92, номер 7, задача 4")
12 ∙ 2 = 24 (км) – велосипедисту еще нужно проехать.
Ответ: 24 км всего ещё нужно проехать велосипедисту.
Задача 5:
В корзине 18 кг яблок, а груш в 3 раза меньше. Сколько кг груш в корзине?
.jpg "Изображение математика 4 класс Моро, Бантова - 2 часть страница 92, номер 7, задача 5")
18 : 3 = 6 (кг) – груш лежат в корзине.
Ответ: 6 кг груш всего лежало в велосипеде.
Задача 6:
В автобусе 30 взрослых, а детей 10. Во сколько раз больше взрослых в автобусе, чем детей?
.jpg "Изображение математика 4 класс Моро, Бантова - 2 часть страница 92, номер 7, задача 6")
30 : 10 = 3 (раза) – во столько раз в автобусе больше взрослых, чем детей.
Ответ: в 3 раза больше в автобусе взрослых, чем детей.
Задача 7:
Длина прямоугольного бассейна 8 м, а ширина 3 м. Длина стороны квадратной площадки 2 м. Во сколько раз площадь площадки меньше площади бассейна?
.jpg "Изображение математика 4 класс Моро, Бантова - 2 часть страница 92, номер 7, задача 7")
1) 8 ∙ 3 = 24 (м²) – площадь бассейна.
2) 2 ∙ 2 = 4 (м²) – площадь площадки.
3) 24 : 4 = 6 (раз) – во столько раз площадь площадки меньше, чем площадь бассейна.
Ответ: в 6 раз площадь площадки больше площади бассейна.
Повтори, как узнать во сколько раз больше или меньше, случаи вне табличного умножения, а также способы оформления краткой записи к задаче.
Шаг 1.
Составляем условие первой задачи.
Купили 5 альбомов по цене 25 р. Узнай стоимость покупки.
Оформляем условие в виде краткой записи.
5 альбомов за ? р.
1 альбом – 25 р.
Рассуждаем.
Узнаем, сколько денег потратили на всю покупку. Для этого стоимость одного альбома умножаем на количество альбомов.
25 ∙ 5 = 125 (р.)
Записываем ответ.
Ответ: 125 рублей потратили на всю покупку.
Шаг 1.
Составляем условие второй задачи.
В бочке 300 л воды, а в ведре 10 л. Сколько раз по 10 л содержится в 300 л?
Оформляем условие в виде краткой записи.
В бочке – 300 л
В ведре – 10 л
? раз по 10 л в 300 л
Рассуждаем.
Узнаем, сколько раз по 10 литров содержится в 300 литрах.
300 : 10 = 30 (раз)
Записываем ответ.
Ответ: 30 раз в 300 л содержится по 10 л.
Шаг 1.
Составляем условие третей задачи.
Длина тесьмы 56 см. Сколько см получится в каждой части, если отрезок разделить на 7 одинаковых частей?
Оформляем условие в виде краткой записи.
Длина всего – 56 см
Длина 1 части – ? см = 7 кусков
Рассуждаем.
Чтобы узнать, сколько см получится в каждой части, если отрезок разделить на 7 одинаковых частей, нужно длину всей тесьмы разделить на 7.
56 : 7 = 8 (см)
Записываем ответ.
Ответ: 8 см длина каждого куска, который получился при делении отрезка в 56 см на 7 кусков.
Шаг 1.
Составляем условие четвертой задачи.
Велосипедист проехал 12 км. Ему осталось еще проехать в 2 раза больше. Сколько км велосипедист должен еще проехать?
Оформляем условие в виде краткой записи.
Рассуждаем.
Узнаем, сколько еще км нужно проехать велосипедисту.
12 ∙ 2 = 24 (км)
Записываем ответ.
Ответ: 24 км велосипедисту еще нужно проехать.
Шаг 1.
Составляем условие пятой задачи.
В корзине 18 кг яблок, а груш в 3 раза меньше. Сколько кг груш в корзине?
Оформляем условие в виде краткой записи.
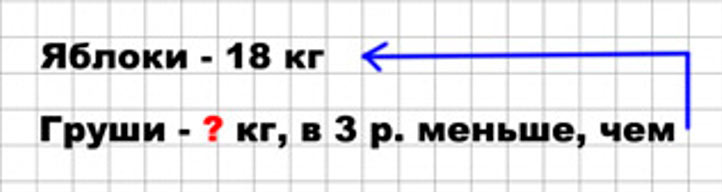
Рассуждаем.
Узнаем, сколько кг груш лежит в корзине.
18 : 3 = 6 (кг)
Записываем ответ.
Ответ: 6 кг груш лежат в корзине.
Шаг 1.
Составляем условие шестой задачи.
В автобусе 30 взрослых, а детей 10. Во сколько раз больше взрослых в автобусе, чем детей?
Оформляем условие в виде краткой записи.
Рассуждаем.
Узнаем, во сколько раз в автобусе больше взрослых, чем детей.
30 : 10 = 3 (раза)
Записываем ответ.
Ответ: в 3 раза во столько раз в автобусе больше взрослых, чем детей.
Шаг 1.
Составляем условие седьмой задачи.
Длина прямоугольного бассейна 8 м, а ширина 3 м. Длина стороны квадратной площадки 2 м. Во сколько раз площадь площадки меньше площади бассейна?
Оформляем условие в виде краткой записи.
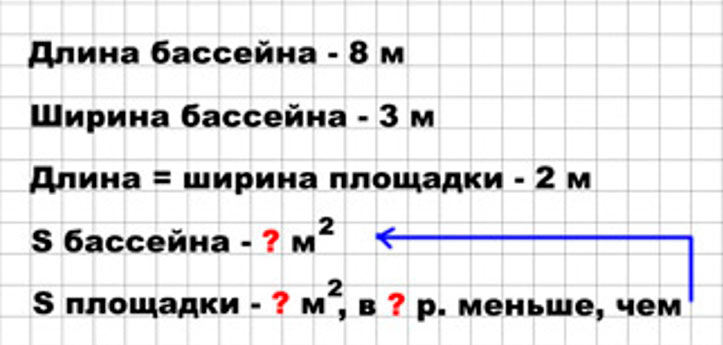
Рассуждаем.
Вычислим площадь бассейна.
1) 8 ∙ 3 = 24 (м²) – площадь бассейна.
Продолжаем рассуждение.
Вычислим площадь площадки.
2) 2 ∙ 2 = 4 (м²) – площадь площадки.
Продолжаем рассуждение.
Вычислим, во сколько раз площадь площадки меньше, чем площадь бассейна.
3) 24 : 4 = 6 (раз)
Записываем ответ.
Ответ: в 6 раз во столько раз площадь площадки меньше, чем площадь бассейна.
Номер 8.
Что получится, если 1) произведение двух чисел разделить на один из множителей; 2) умножить делитель на частное; 3) разделить делимое на частное?
Ответ:1) Получится другой множитель. 2) Получится делимое. 3) Получится делитель.
Повтори, как называются числа при умножении и делении.
Рассуждаем.
• Если произведение двух чисел разделить на один из множителей, то получится другой множитель.
• Если делитель умножить на частное, то получится делимое.
• Если делимое разделить на частное, то получится делитель.
Оформляем задание в тетрадь .
1) Получится другой множитель.
2) Получится делимое.
3) Получится делитель.
Номер 9.
1) Объясни два способа проверки умножения и деления.
2) Вычисли и сделай проверку.
1) Два способа проверки умножения и деления:
а) В первом случае для проверки произведение делят на второй множитель и получают первый, а во втором случае делят на первый множитель и получают второй.
б) В первом случае для проверки частное умножают на делитель и получают делимое, а во втором случае делимое делят на частное и получают делитель.
2)
Повтори алгоритм письменного умножения и деления многозначных чисел, а также как называются числа при умножении и делении.
Рассмотрим данные примеры.
Объясним способы проверки.
Два способа проверки умножения и деления:
а) В первом случае для проверки произведение делят на второй множитель и получают первый, а во втором случае делят на первый множитель и получают второй.
б) В первом случае для проверки частное умножают на делитель и получают делимое, а во втором случае делимое делят на частное и получают делитель.
Выполним вычисления и сделаем проверку.
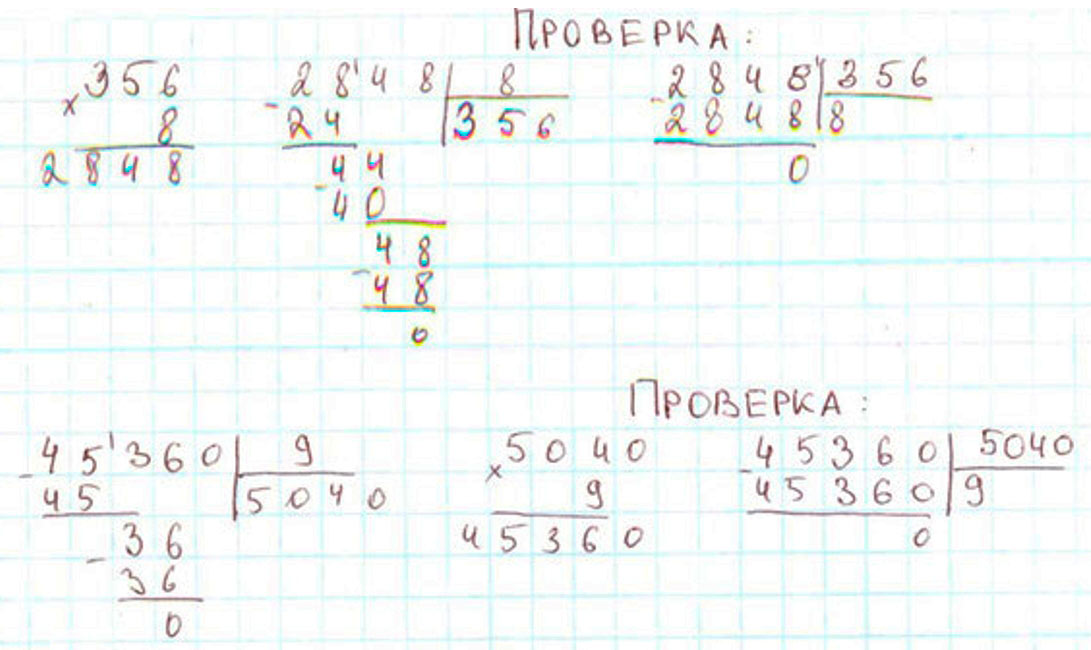
Оформляем задание в тетрадь.
Задание на полях страницы
Ребус.
Ответ:
Повтори случаи табличного умножения.
Заполняем пропуски и выполняем вычисления.
9 ∙ 7 = 63
9 ∙ 3 = 27
9 ∙ 8 = 72
8 ∙ 8 = 64
7 ∙ 3 = 21
6 ∙ 5 = 30
4 ∙ 7 = 28
Оформляем задание в тетрадь.
Арифметические действия
Сложение и вычитание
Номер 1.
Составь и реши задачи на сложение и вычитание, используя слова: «Сколько всего ...?», «Сколько осталось?», «... больше, чем...», «... меньше, чем ...», «На сколько ... больше, чем ...?».
Ответ:Задача 1: Велосипедист в первую половину дня проехал 12 км, а после обеда еще 9 км. Сколько всего км проехал велосипедист?
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 92, номер 1, задача 1, 2024 год.")
12 + 9 = 21 (км)
Ответ: 21 км всего проехал велосипедист.
Задача 2:
В магазин привезли 83 кг фруктов, за день продали 34 кг фруктов. Сколько кг фруктов осталось продать?
Привезли – 83 кг
Продали – 34 кг
Осталось продать – ? кг
83 − 34 = 49 (кг)
Ответ: 49 кг фруктов осталось продать всего.
Задача 3:
В первом классе 20 учеников, во втором на 2 ученика больше, чем в первом классе. Сколько учеников во втором классе?
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 92, номер 1, задача 3, 2024 год.")
20 + 2 = 22 (уч.)
Ответ: 22 ученика всего во втором классе.
Задача 4:
В одной бочке 300 л воды, а в другой бочке на 28 л больше, чем в первой. В третьей бочке на 35 л воды меньше чем во второй бочке. Сколько литров воды всего в бочках?
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 92, номер 1, задача 4, 2024 год.")
1) 300 + 28 = 328 (л) – во второй бочке.
2) 328 − 35 = 293 (л) – в третьей бочке.
3) 300 + 328 + 293 = 921 (л) – всего.
Ответ: 921 л воды всего в бочках.
Задача 5:
В вагоне едут 35 взрослых и 15 детей. На сколько взрослых больше, чем детей?
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 92, номер 1, задача 5, 2024 год.")
35 − 15 = 20 (чел.) – на столько больше взрослых в автобусе, чем детей.
Ответ: на 20 человек больше взрослых в автобусе, чем детей.
Номер 2.
Вспомни, как называются знаки, которые обозначают сложение и вычитание, и выражения, в которых числа соединены знаком сложения; знаком вычитания. Приведи примеры.
Ответ:
Знак, который обозначает сложение, называется плюс (+).
Выражения, в которых знаки соединены знаком сложения (плюсом) называют суммой, например:
16 + 12 = 28;
10 + 260 = 270.
Знак, который обозначает вычитание, называется минус (–).
Выражения, в которых знаки соединены знаком вычитания (минусом) называют разностью, например:
30 − 18 = 12;
58 − 24 = 34.
Номер 3.
Как называются при сложении и вычитании данные числа и число, которое получается в результате выполнения действия?
Ответ:
При сложении числа, которые складываем называются первое слагаемое и второе слагаемое, а результат сложения − суммой, например:
5 + 3 = 8, где:
5 − первое слагаемое;
3 − второе слагаемое;
8 − сумма.
При вычитании число, из которого вычитают, называется уменьшаемое, число, которое вычитают − вычитаемое, а результат − разностью, например:
5 − 2 = 3, где:
5 − уменьшаемое;
2 − вычитаемое;
3 − разность.
Номер 4.
Прочитай, используя различные словесные формулировки, следующие равенства:
Ответ:
26 + 8 = 34
1) Двадцать шесть плюс восемь равно тридцать четыре.
2) Сумма двадцать шести и восьми равна тридцати четырем.
3) При сложении двадцати шести и восьми получается тридцать четыре.
4) Если к двадцати шести прибавить восемь, будет тридцать четыре.
5) Первое слагаемое двадцать шесть, второе слагаемое восемь, сумма тридцать четыре.
72 − 14 = 58
1) Семьдесят два минус четырнадцать равно пятьдесят восемь.
2) Разность семидесяти двух и четырнадцати равна пятидесяти восьми.
3) При вычитании четырнадцати из семидесяти двух получается пятьдесят восемь.
4) Если от семидесяти двух отнять четырнадцать, будет пятьдесят восемь.
5) Уменьшаемое семьдесят два, вычитаемое четырнадцать, разность пятьдесят восемь.
Номер 5.
Рассмотри примеры и ответь на вопросы: 1) Что получится, если из суммы двух слагаемых вычесть одно из них? 2) Что получится, если к разности прибавить вычитаемое? 3) Что получится, если из уменьшаемого вычесть разность?
Сумма = слагаемое 1 + слагаемое 2
Слагаемое 1 = сумма − слагаемое 2
Слагаемое 2 = сумма − слагаемое 1
Уменьшаемое - вычитаемое = разность
Вычитаемое = уменьшаемое − разность
Уменьшаемое = вычитаемое + разность
1) Если из суммы двух слагаемых вычесть одно из них, то получится другое слагаемое.
2) Если к разности прибавить вычитаемое, то получится уменьшаемое.
3) Если из уменьшаемого вычесть разность, то получится вычитаемое.
Номер 6.
После того как из числа 600 вычли задуманное число, получили 170. Какое число задумали?
Ответ:
600 − х = 170
х = 600 − 170
х = 430
Задумали число 430.
Проверка:
600 − 430 = 170 − верно.
Ответ: 430.
Номер 7.
1) Объясни два способа проверки сложения и вычитания.
2) Вычисли и сделай проверку.
3) Найди сумму и проверь различными способами.
1) Пример 1
В первом случае для проверки из суммы вычитают второе слагаемое и получают первое, а во втором случае вычитают первое и получают второе.
Пример 2
В первом случае для проверки к вычитаемому прибавляют разность и получают уменьшаемое, а во втором случае из уменьшаемого вычитают разность и получат вычитаемое.
2)
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 92, номер 7, задание 2, 2024 год.")
3)
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 92, номер 7, задание 3, 2024 год.")
Задание на полях страницы
Ребус.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽
Напишите свой комментарий.