Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 91

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 8.
Объясни, как можно узнать:
1) одно из двух слагаемых, если известны сумма и другое слагаемое;
2) уменьшаемое, если известны разность и вычитаемое;
3) вычитаемое, если известны уменьшаемое и разность.
1) Если известна сумма и другое слагаемое, то, чтобы найти одно из слагаемых, нужно из суммы вычесть другое слагаемое. Например: х + 17 = 34 х = 34 − 17 х = 17 2) Чтобы найти неизвестное уменьшаемое, зная разность и вычитаемое, нужно к разности прибавить вычитаемое. Например, х − 13 = 10 х = 10 + 13 х = 23 3) Чтобы найти неизвестное вычитаемое, зная уменьшаемое и разность, нужно от уменьшаемого отнять разность. Например, 33 − х = 30 х = 33 − 30 х = 3
Повтори, как называются числа при сложении и вычитании.
Рассуждаем.
Если известна сумма и другое слагаемое, то, чтобы найти одно из слагаемых, нужно из суммы вычесть другое слагаемое.
Например: х + 17 = 34
х = 34 − 17
х = 17
Продолжаем рассуждение.
Чтобы найти неизвестное уменьшаемое, зная разность и вычитаемое, нужно к разности прибавить вычитаемое.
Например, х − 13 = 10
х = 10 + 13
х = 23
Продолжаем рассуждение.
Чтобы найти неизвестное вычитаемое, зная уменьшаемое и разность, нужно от уменьшаемого отнять разность.
Например, 33 − х = 30
х = 33 − 30
х = 3
Номер 9.
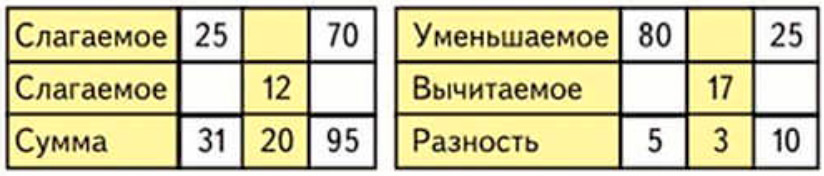
Заполни таблицы.


1 слагаемое + 2 слагаемое = сумма
1 слагаемое = сумма − 2 слагаемое
2 слагаемое = сумма − 1 слагаемое
31 − 25 = 6 (нужно найти неизвестное слагаемое, зная сумму и другое слагаемое)
20 − 12 = 8 (нужно найти неизвестное слагаемое, зная сумму и другое слагаемое)
95 − 70 = 25 (нужно найти неизвестное слагаемое, зная сумму и другое слагаемое)
Уменьшаемое − вычитаемое = разность
Вычитаемое = уменьшаемое − разность
Уменьшаемое = вычитаемое + разность
80 − 5 = 75 (нужно найти незвестное вычитаемое, зная уменьшаемое и разность)
17 + 3 = 20 (нужно найти неизвестное уменьшаемое, зная вычитаемое и разность)
25 − 10 = 15 (нужно найти неизвестное вычитаемое, зная уменьшаемое и разность)
Повтори, как называются числа при сложении и вычитании.
Рассуждаем и выполняем вычисления.
1 слагаемое + 2 слагаемое = сумма
1 слагаемое = сумма − 2 слагаемое
2 слагаемое = сумма − 1 слагаемое
31 − 25 = 6 (нужно найти неизвестное слагаемое, зная сумму и другое слагаемое)
20 − 12 = 8 (нужно найти неизвестное слагаемое, зная сумму и другое слагаемое)
95 − 70 = 25 (нужно найти неизвестное слагаемое, зная сумму и другое слагаемое)
Уменьшаемое − вычитаемое = разность
Вычитаемое = уменьшаемое − разность
Уменьшаемое = вычитаемое + разность
80 − 5 = 75 (нужно найти неизвестное вычитаемое, зная уменьшаемое и разность)
17 + 3 = 20 (нужно найти неизвестное уменьшаемое, зная вычитаемое и разность)
25 − 10 = 15 (нужно найти неизвестное вычитаемое, зная уменьшаемое и разность)
Оформляем задание в тетрадь .
Номер 10.
Реши уравнения.
Ответ:
х − 59 = 76
х - неизвестное уменьшаемое
Чтобы найти неизвестное, нужно к вычитаемому прибавить разность.
х = 76 + 59
х = 135
Ответ: 135.
84 − х = 43
х - неизвестное вычитаемое
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
х = 84 − 43
х = 41
Ответ: 41.
х + 48 = 95
х - неизвестное слагаемое
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть другое слагаемое.
х = 95 − 48
х = 47
Ответ: 47.
34 + х = 82
х - неизвестное слагаемое
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть другое слагаемое.
х = 82 − 34
х = 48
Ответ: 48.
Повтори, как решать уравнения.
Рассуждаем и выполняем вычисления.
х − 59 = 76
х – неизвестное уменьшаемое
Чтобы найти неизвестное, нужно к вычитаемому прибавить разность.
х = 76 + 59
х = 135
Ответ: 135.
84 − х = 43
х – неизвестное вычитаемое
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
х = 84 − 43
х = 41
Ответ: 41.
х + 48 = 95
х – неизвестное слагаемое
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть другое слагаемое.
х = 95 − 48
х = 47
Ответ: 47.
34 + х = 82
х – неизвестное слагаемое
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть другое слагаемое.
х = 82 − 34
х = 48
Ответ: 48.
Оформляем задание в тетрадь.
Номер 11.
Объясни, что означают записи на полях, и реши уравнения.
Ответ:
а + 0 = а
Если к числу прибавить нуль, то получается это же число.
0 + а = а
Если к нулю прибавить число, то значение суммы будет равно данному числу.
с − 0 = с
Если из числа вычесть нуль, то получится это же число.
b − b = 0
Если из числа вычесть само себя, то получится нуль.
156 − х = 156
При вычитании из 156 х получилось 156, то есть при вычитании из числа получилось это же число, а такое происходит, когда вычитаемое равно нулю.
х = 156 − 156
х = 0
Ответ: 0.
х + 267 = 267
Мы видим, что к х прибавляется число 267, а значение суммы равно 267. Такое возможно при прибавлении числа к нулю.
х = 267 − 267
х = 0
Ответ: 0.
987 + х = 987
Мы видим, что к 987 прибавляется х, а значение суммы равно 987, то есть первому слагаемому. Такое возможно при прибавлении числа к нулю.
х = 987 − 987
х = 0
Ответ: 0.
х − 17 = 0
Мы видим, что при вычитании из х 17 получается нуль. Такое возможно, когда уменьшаемое и вычитаемое равны.
х = 17 + 0
х = 17
Ответ: 17.
Повтори, как решать уравнения и что такое буквенные выражения.
Объясним, что означают записи на полях.
а + 0 = а
Если к числу прибавить нуль, то получается это же число.
0 + а = а
Если к нулю прибавить число, то значение суммы будет равно данному числу.
с − 0 = с
Если из числа вычесть нуль, то получится это же число.
b − b = 0
Если из числа вычесть само себя, то получится нуль.
Решим уравнения.
156 − х = 156
При вычитании из 156 х получилось 156, то есть при вычитании из числа получилось это же число, а такое происходит, когда вычитаемое равно нулю.
х = 156 − 156
х = 0
Ответ: 0.
х + 267 = 267
Мы видим, что к х прибавляется число 267, а значение суммы равно 267. Такое возможно при прибавлении числа к нулю.
х = 267 − 267
х = 0
Ответ: 0.
987 + х = 987
Мы видим, что к 987 прибавляется х, а значение суммы равно 987, то есть первому слагаемому. Такое возможно при прибавлении числа к нулю.
х = 987 − 987
х = 0
Ответ: 0.
х − 17 = 0
Мы видим, что при вычитании из х 17 получается нуль. Такое возможно, когда уменьшаемое и вычитаемое равны.
х = 17 + 0
х = 17
Ответ: 17.
Оформляем задание в тетрадь.
Номер 12.
Найди значения выражений.
Ответ:
1970 + 0 = 1970
1970 − 0 = 1970
239 + (437 − 437) = 239 + 0 = 239
365 − (260 + 105) = 365 − 365 = 0
560 − (260 + 300) + 99 = 560 − 560 + 99 = 0 + 99 = 99
(87 − 87) + (78 − 78) = 0 + 0 = 0
Повтори порядок действий.
♦ Если одно из двух слагаемых равно нулю, то сумма равна другому слагаемому.
♦ Если из числа вычесть ноль, то получится число, из которого вычитали.
♦ Если уменьшаемое и вычитаемое равны, то разность равна нулю.
Выполняем вычисления.
1970 + 0 = 1970
1970 − 0 = 1970
239 + (437 − 437) = 239 + 0 = 239
365 − (260 + 105) = 365 − 365 = 0
560 − (260 + 300) + 99 = 560 − 560 + 99 = 0 + 99 = 99
(87 − 87) + (78 − 78) = 0 + 0 = 0
Оформляем задание в тетрадь .
Номер 13.
Чему равна сумма двух слагаемых, если одно из них равно нулю? Чему равна разность, если вычитаемое равно нулю?
Ответ:Если одно из слагаемых равно нулю, то их сумма равна другому слагаемому. а + 0 = а Если вычитаемое равно нулю, то разность равна уменьшаемому. с − 0 = с
Повтори, как называются числа при сложении и вычитании.
Рассуждаем.
Если одно из слагаемых равно нулю, то их сумма равна другому слагаемому.
а + 0 = а
Если вычитаемое равно нулю, то разность равна уменьшаемому.
с − 0 = с
Оформляем задание в тетрадь.
а + 0 = а
с − 0 = с
Номер 14.
Приведи примеры, когда сумма двух слагаемых равна одному из них; когда разность равна уменьшаемому; когда разность равна нулю.
Ответ:Сумма двух слагаемых равна одному из слагаемых, когда другое равно нулю. Например: 7 + 0 = 7; 51 + 0 = 51; 46 + 0 = 46. Разность равна уменьшаемому в том случае, когда вычитаемое равно нулю. Например: 65 − 0 = 65; 77 − 0 = 77; 1 − 0 = 1. Разность равна нулю в том случае, когда уменьшаемое и вычитаемое равны. Например: 67 − 67 = 0; 45 − 45 = 0.
Повтори, как называются числа при сложении и вычитании.
♦ Если одно из двух слагаемых равно нулю, то сумма равна другому слагаемому.
♦ Если из числа вычесть ноль, то получится число, из которого вычитали.
♦ Если уменьшаемое и вычитаемое равны, то разность равна нулю.
Рассуждаем и выполняем вычисления.
Сумма двух слагаемых равна одному из слагаемых, когда другое равно нулю.
Например: 7 + 0 = 7; 51 + 0 = 51; 46 + 0 = 46.
Разность равна уменьшаемому в том случае, когда вычитаемое равно нулю.
Например: 65 − 0 = 65; 77 − 0 = 77; 1 − 0 = 1.
Разность равна нулю в том случае, когда уменьшаемое и вычитаемое равны.
Например: 67 − 67 = 0; 45 − 45 = 0.
Оформляем задание в тетрадь .
Сумма двух слагаемых равна одному из них:
7 + 0 = 7.
51 + 0 = 51
Разность равна уменьшаемому:
65 – 0 = 65.
Разность равна нулю:
67 – 67 = 0.
Номер 15.
Какие свойства сложения ты знаешь (с. 120)? Объясни, почему верны следующие равенства:
16 + 75 = 75 + 16
8 + 17 + 3 = 8 + 20
1) От перестановки слагаемых сумма не меняется. 2) Два соседних слагаемых можно заменить их суммой. Равенство 16 + 75 = 75 + 16 верно на основании переместительного свойства сложения. Равенство 8 + 17 + 3 = 8 + 20 верно на основании того, что два соседних слагаемых можно заменять их суммой.
Повтори свойства сложения.
Рассуждаем.
1) От перестановки слагаемых сумма не меняется.
2) Два соседних слагаемых можно заменить их суммой.
Равенство 16 + 75 = 75 + 16 верно на основании переместительного свойства сложения.
Равенство 8 + 17 + 3 = 8 + 20 верно на основании того, что два соседних слагаемых можно заменять их суммой.
Оформляем задание в тетрадь .
Свойства сложения:
1) От перестановки слагаемых сумма не изменяется:
16 + 75 = 75 + 16.
2) Два соседних слагаемых можно заменять их суммой:
8 + 17 + 3 = 8 + 20, так как 17 + 3 = 20.
Номер 16.
Используя и перестановку, и группировку слагаемых, числа можно складывать в любом порядке. Объясни, как можно легче выполнить сложение.
Ответ:54 + 18 + 26 + 2 = (54 + 26) + (18 + 2) = 80 + 20 = 100 27 + 16 + 13 + 7 + 3 + 14 = (27 + 3) + (16 + 14) + (13 + 7) = 30 + 30 + 20 = 80
Повтори свойства сложения.
Выполняем вычисления удобным способом.
54 + 18 + 26 + 2 = (54 + 16) + (18 + 2) = 70 + 20 = 90
27 + 16 + 13 + 7 + 3 + 14 = (27 + 3) + (16 + 14) + (13 + 7) = 30 + 30 + 20 = 80
Оформляем задание в тетрадь.
Задание на полях страницы
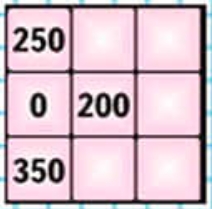
Магический квадрат.

Ответ:

Проверка:
250 + 300 = 50 = 300 + 300 = 600
0 + 200 + 400 = 0 + 600 = 600
350 + 100 + 150 = 500 + 100 = 600
250 + 0 + 350 = 0 = 600 = 600
300 + 200 + 100 = 500 + 100 = 600
50 + 400 + 150 = 200 + 400 = 600
250 + 200 + 150 = 400 + 200 = 600
350 + 200 + 50 = 400 + 200 = 600
Магический квадрат – таблица, заполненная различными числами таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях одинакова.
Выполняем вычисления.
250 + 0 + 350 = 600
600 – (0 + 200) = 400
600 – (350 + 200) = 50
600 – (250 + 50) = 300
600 – (400 + 50) = 150
600 – (300 + 200) = 100
Оформляем задание в тетрадь.
Выражения и уравнения
Номер 1.
Как называют следующие выражения:
Ответ:Это числовые выражения. 40 + 23 = 63 – сумма. 100 − 95 = 5 – разность. 30 ∙ 5 = 150 – произведение. 75 : 3 = 25 – частное.
Номер 2.
Выпиши в один столбик числовые выражения, а в другой – буквенные.
Ответ:
Номер 3.
Найди значения записанных выше числовых выражения и объясни, что обозначают буквы в записях математических выражений.
Ответ:
75 + 38 = 113
83 − 36 = 47
360 : 4 ∙ 6 = 90 ∙ 6 = 540
125 : 5 ∙ (130 − 80) = 25 ∙ 50 = 1250
с + 175 : с – первое слагаемое.
a + b : a – первое слагаемое, b – второе слагаемое.
k − 20 : k – уменьшаемое.
c − d : c – уменьшаемое, d – вычитаемое.
180 ∙ b : b – второй множитель.
k ∙ b : k – первый множитель, b – второй множитель.
450 : с : с – делитель.
а : d : а – делимое, d – делитель.
Номер 4.
Сравни: чем похожи и чем различаются записи в каждом столбике?
Ответ:
Похожи записи в первом и втором столбике тем, что эти записи – математические выражения.
Различия записей в первом и втором столбике состоит в том, что в левом столбике записаны равенства, а в правом записаны неравенства.
160 + 30 = 300 − 110
190 = 190
1 м² = 100 дм²
100 дм² = 100 дм²
260 − 160 < 800 : 4
100 < 200
70 ∙ 7 + 70 < 70 ∙ 9
70 ∙ 8 < 70 ∙ 9
Номер 5.
Приведи пример уравнения.
Объясни, что значит решить уравнение.
Какое число является решением уравнения 87 - х = 80?
Пример: х + 2 = 3
Решить уравнение – это значит найти такое значение переменной, чтобы равенство стало верным.
87 − х = 80
х = 87 − 80
x = 7
Номер 6.
Среди следующих записей найди уравнения. Почему другие записи нельзя назвать уравнениями?
Ответ:
Уравнения:
25 : х = 5
х = 25 : 5
х = 5
56 − а = 50
a = 56 − 50
a = 6
с : 12 = 3
c = 12 ∙ 3
c = 36
Прочие записи не являются уравнениями, потому что уравнение - равенство, в котором неизвестен один компонент, который нужно найти и получить решение уравнения.
Номер 7.
Реши уравнения.
Ответ:
150 : х = 30
х = 150 : 30
х = 5
Проверка:
150 : 5 = 30
30 = 30
Ответ: х = 5
13 ∙ х = 91
х = 91 : 13
х = 7
Проверка:
13 * 7 = 91
91 = 91
Ответ: х = 7
Номер 8.
На диаграмме показана вместимость трёх сосудов: бидона, бака и канистры.
1) Во сколько раз вместимость бидона больше, чем вместимость канистры?
2) На сколько литров вместимость бака меньше, чем вместимость канистры?

Бидон – 60 л
Бак – 15 л
Канистра – 30 л
1) 60 : 30 = 2 (раза) – во сколько раз вместимость бидона больше, чем вместимость канистры;
2) 30 – 15 = 15 (л) – на сколько литров вместимость бака меньше, чем вместимость канистры.
Ответ: 1) в 2 раза вместимость бидона больше, чем вместимость канистры; 2) на 15 л вместимость бака меньше, чем вместимость канистры.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.