Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 90

Учебник 2 часть. Математика 4 класс. Учебник Моро.

Тип: ГДЗ, Решебник.
Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
Часть: 2.
Год: 2020-2024.

Серия: Школа России (ФГОС).
Издательство: Просвещение.

Автор

Материал подготовила:

Ольга Дмитриева

Отличается задание? Переключите год учебника.

2020 2024

Математика 4 класс Моро 2 часть страница 90

Арифметические действия

Сложение и вычитание

Номер 1.

Составь и реши задачи на сложение и вычитание, используя слова: «Сколько всего ...?», «Сколько осталось?», «... больше, чем...», «... меньше, чем ...», «На сколько ... больше, чем ...?».

Ответ:

Задача 1: Велосипедист в первую половину дня проехал 12 км, а после обеда еще 9 км. Сколько всего км проехал велосипедист? математика 4 класс Моро, Бантова - 2 часть страница 90, номер 1, задача 1
12 + 9 = 21 (км) - всего проехал велосипедист
Ответ: 21 км всего проехал велосипедист.
Задача 2: В магазин привезли 83 кг фруктов, за день продали 34 кг фруктов. Сколько кг фруктов осталось продать?
Привезли – 83 кг Продали – 34 кг Осталось продать – ? кг
83 − 34 = 49 (кг) - фруктов осталось продать всего
Ответ: 49 кг фруктов осталось продать всего.
Задача 3: В первом классе 20 учеников, во втором на 2 ученика больше, чем в первом классе. Сколько учеников во втором классе? математика 4 класс Моро, Бантова - 2 часть страница 90, номер 1, задача 3
20 + 2 = 22 (уч.) - во втором классе всего.
Ответ: 22 ученика всего во втором классе.
Задача 4: В одной бочке 300 л воды, а в другой бочке на 28 л больше, чем в первой. В третьей бочке на 35 л воды меньше чем во второй бочке. Сколько литров воды всего в бочках? математика 4 класс Моро, Бантова - 2 часть страница 90, номер 1, задача 4
1) 300 + 28 = 328 (л) – во второй бочке. 2) 328 − 35 = 293 (л) – в третьей бочке. 3) 300 + 328 + 293 = 921 (л) – воды всего.
Ответ: 921 л воды в бочках всего.
Задача 5: В вагоне едут 35 взрослых и 15 детей. На сколько взрослых больше, чем детей? математика 4 класс Моро, Бантова - 2 часть страница 90, номер 1, задача 5
35 − 15 = 20 (чел.) – на столько больше взрослых в автобусе, чем детей.
Ответ: на 20 человек больше взрослых в автобусе, чем детей.

Подсказка:

Повтори способы оформления краткой записи к задаче.

Задача 1.

Шаг 1.
Составляем условие первой задачи.

Велосипедист в первую половину дня проехал 12 км, а после обеда еще 9 км. Сколько всего км проехал велосипедист?

Шаг 2.
Оформляем условие в виде краткой записи.

Шаг 3.
Рассуждаем.

Чтобы узнать сколько всего км проехал велосипедист, нужно сложить расстояния, которые он проехал до и после обеда.
12 + 9 = 21 (км)

Шаг 4.
Записываем ответ.

Ответ: 21 км всего проехал велосипедист.

Задача 2.

Шаг 1.
Составляем условие второй задачи.

В магазин привезли 83 кг фруктов, за день продали 34 кг фруктов. Сколько кг фруктов осталось продать?

Шаг 2.
Оформляем условие в виде краткой записи.

Привезли – 83 кг
Продали – 34 кг
Осталось продать – ? кг

Шаг 3.
Рассуждаем.

Чтобы узнать, сколько фруктов осталось продать, нужно из количества фруктов, которые привезли вычесть количество проданных фруктов.
83 − 34 = 49 (кг)

Шаг 4.
Записываем ответ.

Ответ: 49 кг фруктов осталось продать.

Задача 3.

Шаг 1.
Составляем условие третей задачи.

В первом классе 20 учеников, во втором на 2 ученика больше, чем в первом классе. Сколько учеников во втором классе?

Шаг 2.
Оформляем условие в виде краткой записи.

Шаг 3.
Рассуждаем.

Чтобы узнать, сколько учеников во втором классе, нужно к количеству учеников первого класса добавить два ученика.
20 + 2 = 22 (уч.)

Шаг 4.
Записываем ответ.

Ответ: 22 ученика учится во втором классе.

Задача 4.

Шаг 1.
Составляем условие четвертой задачи.

В одной бочке 300 л воды, а в другой бочке на 28 л больше, чем в первой. В третьей бочке на 35 л воды меньше чем во второй бочке. Сколько литров воды всего в бочках?

Шаг 2.
Оформляем условие в виде краткой записи.

Шаг 3.
Рассуждаем.

Узнаем, сколько литров воды во второй бочке.
1) 300 + 28 = 328 (л) – во второй бочке.

Шаг 4.
Продолжаем рассуждение.

Узнаем, сколько литров воды в третьей бочке.
2) 328 − 35 = 293 (л) – в третьей бочке.

Шаг 5.
Продолжаем рассуждение.

Узнаем, сколько литров воды в трех бочках всего.
3) 300 + 328 + 293 = 921 (л) – всего.

Шаг 6.
Записываем ответ.

Ответ: 921 литров воды в трех бочках.

Задача 5.

Шаг 1.
Составляем условие пятой задачи.

В вагоне едут 35 взрослых и 15 детей. На сколько взрослых больше, чем детей?

Шаг 2.
Оформляем условие в виде краткой записи.

Шаг 3.
Рассуждаем.

Чтобы узнать, на сколько больше взрослых, чем детей в автобусе нужно из количества взрослых вычесть количество детей.
35 − 15 = 20 (чел.)

Шаг 4.
Записываем ответ.

Ответ: на 20 человек больше взрослых в автобусе, чем детей.

Номер 2.

Вспомни, как называются знаки, которые обозначают сложение и вычитание, и выражения, в которых числа соединены знаком сложения; знаком вычитания. Приведи примеры.

Ответ:

Знак, который обозначает сложение, называется плюс (+). Выражения, в которых знаки соединены знаком сложения (плюсом) называют суммой, например: 16 + 12 = 28; 10 + 260 = 270.
Знак, который обозначает вычитание, называется минус (–). Выражения, в которых знаки соединены знаком вычитания (минусом) называют разностью, например: 30 − 18 = 12; 58 − 24 = 34.

Подсказка:

Повтори, как называются выражения при сложении и вычитании.

Шаг 1.
Рассуждаем.

Знак, который обозначает сложение, называется плюс (+).
Выражения, в которых знаки соединены знаком сложения (плюсом) называют суммой, например:
16 + 12 = 28;
10 + 260 = 270.

Знак, который обозначает вычитание, называется минус (–).
Выражения, в которых знаки соединены знаком вычитания (минусом) называют разностью, например:
30 − 18 = 12;
58 − 24 = 34.

Шаг 2.
Оформляем задание в тетрадь.

Номер 3.

Как называются при сложении и вычитании данные числа и число, которое получается в результате выполнения действия?

Ответ:

При сложении числа, которые складываем называются первое слагаемое и второе слагаемое, а результат сложения − суммой, например: 5 + 3 = 8, где: 5 − первое слагаемое; 3 − второе слагаемое; 8 − сумма.
При вычитании число, из которого вычитают, называется уменьшаемое, число, которое вычитают − вычитаемое, а результат − разностью, например: 5 − 2 = 3, где: 5 − уменьшаемое; 2 − вычитаемое; 3 − разность.

Подсказка:

Повтори, как называются числа при сложении и вычитании.

Шаг 1.
Назовем компоненты сложения.

При сложении числа, которые складываем, называются первое слагаемое и второе слагаемое, а результат сложения − суммой, например:
5 + 3 = 8, где:
5 − первое слагаемое;
3 − второе слагаемое;
8 − сумма.

Шаг 2.
Назовем компоненты вычитания.

При вычитании число, из которого вычитают, называется уменьшаемое, число, которое вычитают − вычитаемое, а результат − разностью, например:
5 − 2 = 3, где:
5 − уменьшаемое;
2 − вычитаемое;
3 − разность.

Шаг 3.
Оформляем задание в тетрадь.

Номер 4.

Прочитай, используя различные словесные формулировки, следующие равенства:

Ответ:

26 + 8 = 34 1) Двадцать шесть плюс восемь равно тридцать четыре. 2) Сумма двадцать шести и восьми равна тридцати четырем. 3) При сложении двадцати шести и восьми получается тридцать четыре. 4) Если к двадцати шести прибавить восемь, будет тридцать четыре. 5) Первое слагаемое двадцать шесть, второе слагаемое восемь, сумма тридцать четыре.
72 − 14 = 58 1) Семьдесят два минус четырнадцать равно пятьдесят восемь. 2) Разность семидесяти двух и четырнадцати равна пятидесяти восьми. 3) При вычитании четырнадцати из семидесяти двух получается пятьдесят восемь. 4) Если от семидесяти двух отнять четырнадцать, будет пятьдесят восемь. 5) Уменьшаемое семьдесят два, вычитаемое четырнадцать, разность пятьдесят восемь.

Подсказка:

Повтори, как называются числа при сложении и вычитании.

Шаг 1.
Прочитаем первое равенство .

Шаг 2.
Прочитаем второе равенство.

72 − 14 = 58
1) Семьдесят два минус четырнадцать равно пятьдесят восемь.
2) Разность семидесяти двух и четырнадцати равна пятидесяти восьми.
3) При вычитании четырнадцати из семидесяти двух получается пятьдесят восемь.
4) Если от семидесяти двух отнять четырнадцать, будет пятьдесят восемь.
5) Уменьшаемое семьдесят два, вычитаемое четырнадцать, разность пятьдесят восемь.

Номер 5.

Рассмотри примеры и ответь на вопросы: 1) Что получится, если из суммы двух слагаемых вычесть одно из них? 2) Что получится, если к разности прибавить вычитаемое? 3) Что получится, если из уменьшаемого вычесть разность?

Ответ:

Сумма = слагаемое 1 + слагаемое 2 Слагаемое 1 = сумма − слагаемое 2 Слагаемое 2 = сумма − слагаемое 1
Уменьшаемое - вычитаемое = разность Вычитаемое = уменьшаемое − разность Уменьшаемое = вычитаемое + разность
1) Если из суммы двух слагаемых вычесть одно из них, то получится другое слагаемое. 2) Если к разности прибавить вычитаемое, то получится уменьшаемое. 3) Если из уменьшаемого вычесть разность, то получится вычитаемое.

Подсказка:

Повтори, как называются числа при сложении и вычитании.

Шаг 1.
Рассмотрим примеры.

Шаг 2.
Ответим на вопросы.

Сумма = слагаемое 1 + слагаемое 2
Слагаемое 1 = сумма – слагаемое 2
Слагаемое 2 = сумма – слагаемое 1

Уменьшаемое – вычитаемое = разность
Вычитаемое = уменьшаемое – разность
Уменьшаемое = вычитаемое + разность

1) Если из суммы двух слагаемых вычесть одно из них, то получится другое слагаемое.
2) Если к разности прибавить вычитаемое, то получится уменьшаемое.
3) Если из уменьшаемого вычесть разность, то получится вычитаемое.

Номер 6.

После того как из числа 600 вычли задуманное число, получили 170. Какое число задумали?

Ответ:

600 − х = 170 х = 600 − 170 х = 430 Задумали число 430. Проверка: 600 − 430 = 170 − верно.
Ответ: 430.

Подсказка:

Повтори, как решать уравнения.

Шаг 1.
Найдем число, которое задумали.

600 − х = 170
х = 600 − 170
х = 430
Задумали число 430.
Проверка:
600 − 430 = 170 – верно.
Ответ: 430.

Шаг 2.
Оформляем задание в тетрадь.

Номер 7.

1) Объясни два способа проверки сложения и вычитания.
2) Вычисли и сделай проверку.
3) Найди сумму и проверь различными способами.

Ответ:

1) Пример 1 В первом случае для проверки из суммы вычитают второе слагаемое и получают первое, а во втором случае вычитают первое и получают второе. Пример 2 В первом случае для проверки к вычитаемому прибавляют разность и получают уменьшаемое, а во втором случае из уменьшаемого вычитают разность и получат вычитаемое.
2)

математика 4 класс Моро, Бантова - 2 часть страница 90, номер 7, задание 2

математика 4 класс Моро, Бантова - 2 часть страница 90, номер 7, задание 3

Подсказка:

Повтори алгоритм письменного сложения и вычитания многозначных чисел, а также порядок действий.

Шаг 1.
Объясним способы проверки сложения и вычитания.

Пример 1
В первом случае для проверки из суммы вычитают второе слагаемое и получают первое, а во втором случае вычитают первое и получают второе.
Пример 2
В первом случае для проверки к вычитаемому прибавляют разность и получают уменьшаемое, а во втором случае из уменьшаемого вычитают разность и получат вычитаемое.

Шаг 2.
Вычислим примеры и сделаем проверку.

Шаг 3.
Найдем сумму и проверим различными способами.

Задание на полях страницы

Ребус.

Ответ:

Подсказка:

Повтори алгоритм письменного сложения и вычитания многозначных чисел.

Ребус 1.

Шаг 1.
Рассмотрим ребус.

Шаг 2.
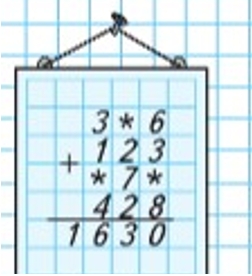
Разгадаем ребус.

Складываю единицы: 6 + 3 + 8 = 17. В единицах получилось 0. Значит, нужно добавить число 3, так как 17 + 3 = 20. 2 дес. запомню и прибавлю к десяткам.
Складываю десятки: 2 + 7 + 2 = 11, да еще 2. 11 + 2 = 13. А в десятках получилось 3. Значит, нужно добавить число 0. 1 сот. запомню и прибавлю к сотням.
Складываю сотни: 3 + 1 + 4 = 8, да еще 1. 8 + 1 = 9. А в сотнях получилось 6. Значит, нужно добавить число 7, так как 9 + 7 = 16.

Шаг 3.
Оформим задание в тетрадь.

Ребус 2.

Шаг 1.
Рассмотрим ребус.

Шаг 2.
Разгадаем ребус.

Вычитаю единицы: из 7 нельзя вычесть какое-то число, чтобы получилось 9. Беру 1 сот. из 5 сот. (Чтобы не забыть об этом, ставлю точку над цифрой 5). 1 сот. = 10 дес. Беру 1 дес. из 10 дес. (Чтобы не забыть об этом, ставлю точку над цифрой 0). 1 дес. и 7 дес. – это 17 ед. Из 17 вычесть 9, получится 8.
Вычитаю десятки: было 10 дес., осталось 9 дес. 9 – 6 = 3.
Вычитаю сотни: было 5 сот., осталось 4 сот. 4 – 0 = 4.
Вычитаю тысячи: 2 – 1 = 1

Шаг 3.
Оформим задание в тетрадь.

Математика 4 класс Моро 2 часть страница 90. 2024 год

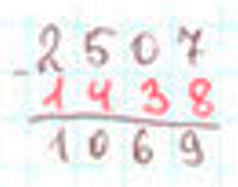
Номер 23.

Заполни пропуски.

Ответ:

2070 дес. = 2070 : 10 = 207 сот., потому что в 1 сот. – 10 дес. 4000 сот. = 4000 ∙ 10 = 40000 дес., потому что в 1 сот. – 10 дес.
251 тыс. тыс. = 251 тыс. тыс. ∙ 1000000 = 251 млн, потому что 1 млн = 1 тыс. тыс. = 1000000 307 тыс. тыс. = 307 тыс. тыс. ∙ 1000000 = 307 млн, потому что 1 млн = 1тыс. тыс. = 1000000

Номер 24.

Сколько всего тысяч в числе 72840? 635017? 175030?
Сколько всего сотен в каждом из этих чисел?
Сколько всего десятков в каждом из них?
Сколько в каждом из этих чисел единиц?

Ответ:

Число 72840 состоит из: 72 тысяч; 728 сотен; 7284 десятков; 72840 единиц.
Число 635017 состоит из: 635 тысяч; 6350 сотен; 63501 десятков; 635017 единиц.
Число 175030 состоит из: 175 тысяч; 1750 сотен; 17503 десятков; 175030 единиц.

Номер 25.

Представь в виде суммы разрядных слагаемых числа: 705004, 108350, 1300807.

Ответ:

705 004 = 700 000 + 5000 + 4
108 350 = 100 000 + 8000 + 300 + 50
1 300 807 = 1 000 000 + 300 000 + 800 + 7

Номер 26.

1) Рассмотри таблицу. Вспомни, как записываются числа римскими цифрами.
2) Вспомни, как записывали числа 4, 6, 9, 11.
3) Попробуй разобраться, какие числа записаны такими римскими цифрами: XX; CX; XL; LX; CM; MC; LXX; XCV; CDL.

Ответ:

2) 4 – IV, 6 – VI, 9 – IX, 11 – XI. 3) XX – 20, потому что Х – 10: 10 + 10 = 20. CX – 110, потому что С – 100, а Х v 10: 100 + 10 = 110. XL − 40; потому что Х – 10, L – 50. Нужно найти число, меньше, чем 50 на 10, потому что Х записано слева: 50 – 10 = 40. LX − 60; потому что Х – 10, L – 50. Нужно найти число, больше, чем 50 на 10, потому что Х записано справа: 50 + 10 = 60. CM − 900; потому что С – 100, а М – 1000. Нужно найти число, меньше, чем 1000 на 100, потому что С записано слева от М: 1000 – 100 = 900. MC − 1100; потому что С – 100, а М – 1000. Нужно найти число, больше, чем 1000 на 100, потому что С записано справа от М: 1000 + 100 = 1100. LXX − 70; потому что Х – 10, L – 50. Нужно найти число, больше, чем 50 на 2 десятка, потому что Х записано дважды справа: 50 + 10 + 10 = 70. XCV − 95; потому что Х – 10, С – 100, а V – 5. Нужно найти число, которое меньше чем 100 на 10, а затем увеличить его на 5, ведь Х записано слева от С, а V справа: 100 – 10 + 5 = 95. CDL − 450. Потому что С – 100, D – 500, а L – 50. Нужно найти число меньше, чем 500 на 100, а затем увеличить его на 50, потому что С записано справа от D, а L слева от него: 500 – 100 + 50 = 450.

Номер 27.

На одной из улиц города туристы увидели два дома, на каждом из которых был обозначен год постройки: на одном доме – MDCCCVII, а на другом – MDCCLXXIX. Какой дом построен раньше?

Ответ:

MDCCCVII = 1000 + 500 + 100 + 100 + 100 + 7 (М – 1000, D − 500, C − 100, а CCC = 100 + 100 + 100 = 300; VII − 5 + 2 = 7) = 1000 + 500 + 300 + 7 = 1807 − год постройки первого здания.
MDCCLXXIX = 1000 + 500 + 100 + 100 + 50 + 29 (М − 1000, D − 500, C − 100, а CC = 100 + 100 = 200; L = 50; ХХIX = 10 + 10 + 9 = 29) = 1000 + 500 + 200 + 50 + 29 = 1779 − год постройки второго здания.
Ответ: второй дом построен раньше первого.

Номер 28.

Запиши римскими цифрами:

1) год рождения А.С. Пушкина – 1799; 2) годы начала и конца Великой Отечественной войны – 1941 и 1945.

Ответ:

1) 1799 = 1000 + 500 + 100 + 100 + 90 + 9     1000 = М     500 = D     100 = C     90 = 100 – 10 = ХС     9 = 10 – 1 = IХ     Ответ: 1799 = MDCCХСIХ.
2) 1941 = 1000 + 900 + 40 + 1     1000 = M     900 = 1000 – 100 = CM     40 = 50 – 10 = XL     1 = I     Ответ: 1941 = MCMXLI.
    1945 = 1000 + 900 + 40 + 5     1000 = M     900 = 1000 – 100 = CM     40 = 50 – 10 = XL     1 = V     Ответ: 1945 = MCMXLV.

Номер 29.

В выложенных из палочек равенствах с римскими цифрами допущены ошибки. Как надо переложить по одной палочке в каждом равенстве, чтобы исправить ошибку? Запиши верные равенства.

Ответ: