Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 87

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 10.
Покажи на примере, что 1000 единиц одного класса образуют единицу следующего класса.
Ответ:1000 единиц − это тысяча, так как 1000 ∙ 1 = 1000 1000 десятков – это десять тысяч, так как 1000 ∙ 10 = 10000
Повтори состав многозначного числа.
Рассуждаем и выполняем вычисления.
1000 единиц − это тысяча, так как 1000 ∙ 1 = 1000
1000 десятков – это десять тысяч, так как 1000 ∙ 10 = 10000
Оформляем задание в тетрадь.
Номер 11.
Объясни, почему с помощью одних и тех же цифр можно записать несколько разных чисел. Записи все возможные четырёхзначные числа с помощью цифр 4, 0, 3, 2, не повторяя в каждом числе ни одной из них. Объясни, что означает цифра 0 в записи каждого из этих чисел.
Ответ:1) Цифры в числах можно менять местами, соответственно, один и тот же разряд будет содержать разные цифры, а это уже разные числа. 2) Все возможные трехзначные числа, записанные с помощью цифр 4, 0, 3 и 2 без повторения: 2034, 2043, 2304, 2340, 2403, 2430, 3024, 3042, 3204, 3240, 3402, 3420, 4023, 4032, 4203, 4230, 4302, 4320. 3) Цифра 0 в записи каждого из этих чисел означает: 2034 – отсутствует разряд сотен, 2043 – отсутствует разряд сотен, 2304 – отсутствует разряд десятков, 2340 – отсутствует разряда единиц, 2403 – отсутствует разряд десятков, 2430 – отсутствует разряда единиц, 3024 – отсутствует разряд сотен, 3042 – отсутствует разряд сотен, 3204 – отсутствует разряд десятков, 3240 – отсутствует разряда единиц, 3402 – отсутствует разряд десятков, 3420 – отсутствует разряда единиц, 4023 – отсутствует разряд сотен, 4032 – отсутствует разряд сотен, 4203 – отсутствует разряд десятков, 4230 – отсутствует разряда единиц, 4302 – отсутствует разряд десятков, 4320 – отсутствует разряда единиц.
Повтори состав многозначного числа.
Рассуждаем и составляем числа по данным задания.
1) Цифры в числах можно менять местами, соответственно, один и тот же разряд будет содержать разные цифры, а это уже разные числа.
2) Все возможные трехзначные числа, записанные с помощью цифр 4, 0, 3 и 2 без повторения:
2034, 2043, 2304, 2340, 2403, 2430, 3024, 3042, 3204, 3240, 3402, 3420, 4023, 4032, 4203, 4230, 4302, 4320.
3) Цифра 0 в записи каждого из этих чисел означает:
2034 – отсутствует разряд сотен,
2043 – отсутствует разряд сотен,
2304 – отсутствует разряд десятков,
2340 – отсутствует разряда единиц,
2403 – отсутствует разряд десятков,
2430 – отсутствует разряда единиц,
3024 – отсутствует разряд сотен,
3042 – отсутствует разряд сотен,
3204 – отсутствует разряд десятков,
3240 – отсутствует разряда единиц,
3402 – отсутствует разряд десятков,
3420 – отсутствует разряда единиц,
4023 – отсутствует разряд сотен,
4032 – отсутствует разряд сотен,
4203 – отсутствует разряд десятков,
4230 – отсутствует разряда единиц,
4302 – отсутствует разряд десятков,
4320 – отсутствует разряда единиц.
Оформляем задание в тетрадь.
Цифры в числе можно менять местами, так как мы меняем разряды, то получаются другие числа.
2034, 2304, 2340, 2043, 2403, 2430, 3024, 3204, 3240, 3042, 3402, 3420, 4023, 4203, 4230, 4032, 4302, 4320.
Цифра 0 обозначает отсутствие соответствующего разряда.
Номер 12.
Сколько нулей нужно написать после 1, чтобы получилось число одна тысяча? сто тысяч? один миллион?
Ответ:Чтобы получилось число одна тысяча, после 1 надо записать 3 нуля, потому что 1000 больше единицы в 1000 раз. Чтобы получилось число сто тысяч, после 1 надо записать 5 нулей, потому что 100000 больше, чем 1 в 100000 раз. Чтобы получилось число один миллион, после 1 надо написать 6 нулей, потому что число 1000000 больше, чем 1 в 1000000 раз.
Повтори состав многозначного числа.
Рассуждаем.
Чтобы получилось число одна тысяча, после 1 надо записать 3 нуля, потому что 1000 больше единицы в 1000 раз.
Чтобы получилось число сто тысяч, после 1 надо записать 5 нулей, потому что 100000 больше, чем 1 в 100000 раз.
Чтобы получилось число один миллион, после 1 надо написать 6 нулей, потому что число 1000000 больше, чем 1 в 1000000 раз.
Оформляем задание в тетрадь.
1 000 (одна тысяча) – три нуля.
100 000 (сто тысяч) – пять нулей.
1 000 000 (один миллион) – шесть нулей.
Номер 13.
Как получить число, которое в 10, 100, 1000 раз больше данного? Приведи пример.
Ответ:Чтобы получить число, которое в 10 раз больше данного, нужно данное число умножить на 10, например, 7 ∙ 10 = 70. Чтобы получить число, которое в 100 раз больше данного, нужно данное число умножить на 100, например, 7 ∙ 100 = 700. Чтобы получить число, которое в 1000 раз больше данного, нужно данное число умножить на 1000, например, 7 ∙ 1000 = 7000. Умножить число на 10, 100, 1000. Примеры: 5 ∙ 10 = 50, 5 ∙ 100 = 500, 5 ∙ 1000 = 5000.
Повтори, как умножать на круглые числа.
Рассуждаем и выполняем вычисления.
Чтобы получить число, которое в 10 раз больше данного, нужно данное число умножить на 10, например, 7 ∙ 10 = 70.
Чтобы получить число, которое в 100 раз больше данного, нужно данное число умножить на 100, например, 7 ∙ 100 = 700.
Чтобы получить число, которое в 1000 раз больше данного, нужно данное число умножить на 1000, например, 7 ∙ 1000 = 7000.
Умножить число на 10, 100, 1000. Примеры: 5 ∙ 10 = 50, 5 ∙ 100 = 500, 5 ∙ 1000 = 5000.
Оформляем задание в тетрадь.
Нужно данное число умножить соответственно на 10, 100, 1000.
7 ∙ 10 = 70;
7 ∙ 100 = 700;
7 ∙ 1 000 = 7 000.
Номер 14.
Как называется высший разряд в шестизначном числе? в восьмизначном числе?
Ответ:В шестизначном числе высший разряд – сотни тысяч. В восьмизначном – десятки миллионов.
Повтори состав многозначного числа.
Отвечаем на вопросы задания.
1) В шестизначном числе высший разряд – сотни тысяч.
2) В восьмизначном – десятки миллионов.
Оформляем задание в тетрадь.
Номер 15.
Запиши цифрами число 2 миллиона 36 тысяч 5. Объясни, сколько раз пришлось использовать в записи этого числа цифру 0 и почему.
Ответ:2036005. Цифра 0 используется 3 раза. Она означает: 1) отсутствие десятков; 2) отсутствие сотен; 3) отсутствие сотен тысяч.
Повтори состав многозначного числа.
Рассуждаем.
2036005
Цифра 0 используется 3 раза.
Она означает:
1) отсутствие десятков;
2) отсутствие сотен;
3) отсутствие сотен тысяч.
Оформляем задание в тетрадь.
2036 005
Цифра 0 используется 3 раза. Она означает отсутствие в классе единиц разрядов десятков и сотен, а в классе тысяч – числа разряда сотен тысяч.
Номер 16.
Прочитай числа: 3870563027, 17008032, 640003007.
Ответ:3870563027 – три миллиарда восемьсот семьдесят миллионов пятьсот шестьдесят три тысячи двадцать семь. 17008032 – семнадцать миллионов восемь тысяч тридцать два. 640003007 – шестьсот сорок миллионов три тысячи семь.
Повтори состав многозначного числа.
Читаем первое число.
3870563027 – три миллиарда восемьсот семьдесят миллионов пятьсот шестьдесят три тысячи двадцать семь.
Читаем второе число.
17008032 – семнадцать миллионов восемь тысяч тридцать два.
Читаем третье число.
640003007 – шестьсот сорок миллионов три тысячи семь.
Номер 17.
Вспомни разные приёмы сравнения чисел и сравни следующие числа (с. 117):
Ответ:
1) По месту, которое они занимают при счете. Так,
378 < 379, так как 378 встречается при счёте раньше, чем 379.
2) Поразрядно, начиная с высших разрядов. Так,
6572 > 986 , так как высший разряд в числе 6572 – единицы тысяч, а в числе 986 – сотни;
42375 > 39879, так как 4 дес. тыс. > 3 дес. тыс.
Повтори, как сравнивать числа.
Сравниваем числа
1) По месту, которое они занимают при счете. Так,
378 < 379, так как 378 встречается при счёте раньше, чем 379.
2) Поразрядно, начиная с высших разрядов. Так,
6572 > 986 , так как высший разряд в числе 6572 – единицы тысяч, а в числе 986 – сотни;
42375 > 39879, так как 4 дес. тыс. > 3 дес. тыс.
Оформляем задание в тетрадь.
378 < 379
6572 > 986
42375 > 39879
Номер 18.
Сколько ты знаешь чисел, которые меньше числа 57? (Не забудь число 0.) Почему нельзя назвать все числа, которые больше, чем 57?
Ответ:Я знаю 57 чисел меньше числа 57: натуральные числа от 1 до 56 и нуль. Все числа, которые больше, чем 57, назвать нельзя, так как их существует бесконечность.
Повтори, как найти большее или меньшее число.
Рассуждаем.
Я знаю 57 чисел меньше числа 57: натуральные числа от 1 до 56 и нуль.
Все числа, которые больше, чем 57, назвать нельзя, так как их существует бесконечность.
Оформляем задание в тетрадь.
Номер 19.
Назови число, которое следует при счёте за числом 9999; за числом 1000000; за числом 1 миллиард.
Ответ:За числом 9999 следует число 10000 (десять тысяч). 9999 + 1 = 10000 За числом 1000000 – число 1000001 (один миллион один). 1000000 + 1 = 1000001 За числом 1 миллиард – число 1000000001 (один миллиард один). 1000000000 + 1 = 1000000001
Повтори состав многозначного числа.
Рассуждаем и выполняем вычисления.
За числом 9999 следует число 10000 (десять тысяч).
9999 + 1 = 10000
За числом 1000000 – число 1000001 (один миллион один).
1000000 + 1 = 1000001
За числом 1 миллиард – число 1000000001 (один миллиард один).
1000000000 + 1 = 1000000001
Оформляем задание в тетрадь.
Номер 20.
Сколько всего однозначных чисел? двузначных чисел? трёхзначных чисел?
Ответ:Однозначных чисел всего 10 (натуральные числа от 1 до 9 и 0). Двузначных чисел всего 90 (натуральные числа от 10 до 99 включительно). Трехзначных чисел всего 900 (натуральные числа от 100 до 999 включительно).
Повтори состав трёхзначных чисел.
Рассуждаем.
Однозначных чисел всего 10 (натуральные числа от 1 до 9 и 0).
Двузначных чисел всего 90 (натуральные числа от 10 до 99 включительно).
Трехзначных чисел всего 900 (натуральные числа от 100 до 999 включительно).
Оформляем задание в тетрадь.
Однозначных чисел 10, двузначных – 90, трёхзначных – 900.
Номер 21.
Сколько чисел находится между числами 48 и 95?
Ответ:Между числами 48 и 95 находятся: 1) 95 − 48 − 1 = 46 чисел
Повтори состав двузначных чисел.
Выполняем вычисления.
Между числами 48 и 95 находятся:
1) 95 − 48 − 1 = 46 чисел
Оформляем задание в тетрадь.
46 чисел.
Номер 22.
Объясни, как изменится любое трёхзначное число, если в записи его приписать слева цифру 1; 2; 3.
Ответ:Проверим, что станет с числом 500. Приписываем слева 1. Получится 1500. Припишем к 500 слева 2, станет - 2500. Припишем к 500 слева 3, станет 3500. Получается, что мы будто добавляем разряд тысяч к исходному числу и оно становится соответственно больше на 1000, 2000 и 3000 тысячи.
Повтори состав многозначных чисел.
Рассуждаем.
Проверим, что станет с числом 500.
Приписываем слева 1. Получится 1500.
Припишем к 500 слева 2, станет – 2500.
Припишем к 500 слева 3, станет 3500.
Получается, что мы будто добавляем разряд тысяч к исходному числу и оно становится соответственно больше на 1000, 2000 и 3000 тысячи.
Оформляем задание в тетрадь.
Увеличится на 1 000,
увеличится на 2 000,
увеличится на 3 000.
Число станет четырёхзначным.
Задание на полях страницы
Начерти

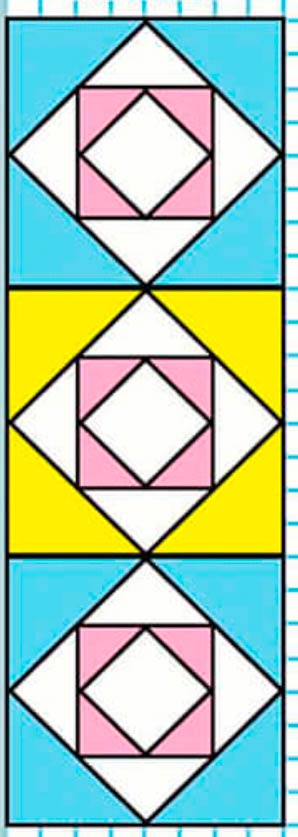
1) Нарисуй в тетради 3 квадрата со стороной 3 см. 2) Соедини середины сторон квадрата линиями. Ты получешь 3 ровных ромба. 3) Теперь соедини середины сторон ромба линиями и получишь три квадратика. 4) Раскрась свой узор.
Повтори, какие бывают многоугольники.
Рассуждаем.
1) Нарисуй в тетради 3 квадрата со стороной 3 см.
2) Соедини середины сторон квадрата линиями. Ты получишь 3 ровных ромба.
3) Теперь соедини середины сторон ромба линиями и получишь три квадратика.
4) Раскрась свой узор.
Оформляем задание в тетрадь.
Номер 28.
1) Запиши названия всех равнобедренных треугольников и подчеркни среди них названия равнобедренных тупоугольных треугольников синим карандашом, а равнобедренных остроугольных – красным.
2) Запиши названия всех четырёхугольников.

1) ABC, AKC, ADC, BAD, BCD. 2) ABCD, AKCD.
Номер 29.
Хватит ли 20 м 50 см ткани, чтобы сшить шторы на 4 окна, если на каждое окно расходуют 2 полосы ткани длиной по 2 м 50 см?
Ответ:
Всего ткани – 20 м 50 см
На 1 окно – 2 полосы по 2 м 50 см
На 4 окна – ? м
1) 2 м 50 см ∙ 2 = 5 (м) – ткани уходит на одно окно.
2) 5 ∙ 4 = 20 (м) – ткани уходит на 4 окна.
3) 20 м < 20 м 50 см.
Ответ: ткани хватит, чтобы сшить шторы на 4 окна.
Номер 30.
В комнате, длина которой 8 м, а ширина на 2 м меньше длины, надо покрасить пол. Сколько для этого понадобится краски, если расходовать по 150 г на 1 м²?
Ответ:
1) 8 − 2 = 6 (м) – ширина комнаты.
2) 6 ∙ 8 = 48 (м²) – площадь комнаты.
3) 48 ∙ 150 = 7200 (г) – 7 кг 200 г – краски понадобится, чтобы покрасить пол в комнате.
Ответ: 7 кг 200 г краски понадобится для покраски пола в комнате.
Номер 31.
Для спортивной школы купили 96 пар лыж по а р. за пару и 84 пары коньков по с р. Объясни, что обозначают выражения:
Ответ:
Лыжи – 96 пар по а р.
Коньки – 84 пары по с р.
1) а ∙ 96 – стоимость всех лыж.
2) с ∙ 84 – стоимость всех коньков.
3) а ∙ 96 + с ∙ 84 – стоимость всей покупки.
Номер 32.
Проверь, верны ли неравенства.
Ответ:
2 т < 200 ц
2 т = 20 ц
20 ц < 200 ц
Значит, 2 т < 200 ц – верно
3 ц > 300 кг
3 ц = 300 кг
300 кг = 300 кг
Значит, 3 ц > 300 кг – неверно
2 сут. > 50 ч
2 сут. = 48 ч
48 ч < 50 ч
Значит, 2 сут. > 50 ч – неверно
3 года < 40 мес.
3 года = 36 мес.
36 мес. < 40 мес.
Значит, 3 года < 40 мес. – верно
2 км² > 2000 м²
2 км² = 2000000 м²
2000000 м2 > 2000 м²
Значит, 2 км² > 2000 м² – верно
5 м² < 100 дм²
5 м² = 500 дм²
500 дм² > 100 дм²
Значит, 5 м² < 100 дм² – неверно
Номер 33.
Реши уравнения.
Ответ:
Номер 34.
1) Во сколько раз сумма чисел 933 и 1167 больше частного чисел 21600 и 72?
2) На сколько произведение чисел 725 и 30 больше разности этих чисел?

Номер 35.
Сейчас 20 ч 48 мин. Сколько времени осталось до конца суток? На сколько больше прошедшая часть суток, чем оставшаяся?
Ответ:
Сутки = 24 ч 1) 24 ч − 20 ч 48 мин = 23 ч 60 мин − 20 ч 48 мин = 3 ч 12 мин − осталось до конца суток. 2) 20 ч 48 мин − 3 ч 12 мин = на 17 ч 36 мин − прошедшая часть суток, больше, чем оставшаяся.
Номер 36.
Сумма трёх чисел 800, первое число 300, оно в 4 раза больше второго числа. Найди третье число.
Ответ:
1) 300 : 4 = 75 – второе число.
2) 300 + 75 = 375 – сумма первого и второго числа.
3) 800 − 375 = 425 – третье число.
Ответ: третье число равно 425.
Номер 37.
1) Рассмотри чертёж. Узнай длину диаметра большего круга, если радиус меньшего круга равен 1 см.
2) Сколько осей симметрии у этой фигуры?

1) Радиус – отрезок, соединяющий центр окружности с точкой, на окружности. Все радиусы равны.
Радиус малого круга = 1 см = ОА.
Сумма двух радиусов равняется диаметру. Если мы продолжим отрезок АО по прямой, то получим отрезок АР, который является диаметром малого круга и радиусом большого круга.
А чтобы найти диаметр большого круга, нужно радиус большого круга умножить на 2, т.е. РМ = 2 см ∙ 2 = 4 см.
Ответ: длина диаметра большего круга равна 4 см.

2) У данной фигуры одна ось симметрии.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.