Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 85

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 28.
1) Запиши названия всех равнобедренных треугольников и подчеркни среди них названия равнобедренных тупоугольных треугольников синим карандашом, а равнобедренных остроугольных – красным.
2) Запиши названия всех четырёхугольников.

Ответ:
1) ABC, AKC, ADC, BAD, BCD. 2) ABCD, AKCD.
Повтори виды углов, треугольников и многоугольников.
Рассмотрим чертеж на полях.
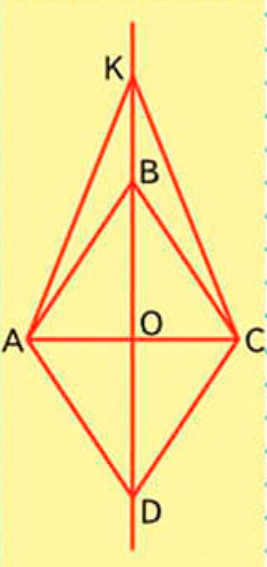
Запишем названия всех равнобедренных треугольников.
Треугольники, у которых две стороны равны, называются равнобедренными.
Острый угол – это угол, который меньше прямого угла.
Тупой угол – это угол, который больше прямого угла.
1) ABC, AKC, ADC, BAD, BCD.
Запишем названия всех четырехугольников.
2) ABCD, AKCD.
Оформляем задание в тетрадь.
Номер 29.
Хватит ли 20 м 50 см ткани, чтобы сшить шторы на 4 окна, если на каждое окно расходуют 2 полосы ткани длиной по 2 м 50 см?
Ответ:
Всего ткани - 20 м 50 см
На 1 окно - 2 полосы по 2 м 50 см
На 4 окна - ? м
1) 2 м 50 см ∙ 2 = 5 (м) – ткани уходит на одно окно.
2) 5 ∙ 4 = 20 (м) – ткани уходит на 4 окна.
3) 20 м < 20 м 50 см.
Ответ: ткани хватит на пошив штор для четырёх окон.
Повтори единицы длины – метр и сантиметр.
Оформляем условие в виде краткой записи.
Всего ткани – 20 м 50 см
На 1 окно – 2 полосы по 2 м 50 см
На 4 окна – ? м
Рассуждаем.
Вычислим, сколько ткани уходит на пошив штор для одного окна.
1) 2 м 50 см ∙ 2 = 5 (м) – ткани уходит на одно окно.
Продолжаем рассуждение.
Вычислим, сколько ткани уходит на пошив штор для четырех окон.
2) 5 ∙ 4 = 20 (м) – ткани уходит на 4 окна.
Продолжаем рассуждение.
Хватит ли ткани на пошив штор?
3) 20 м < 20 м 50 см.
Записываем ответ.
Ответ: хватит ткани.
Номер 30.
В комнате, длина которой 8 м, а ширина на 2 м меньше длины, надо покрасить пол. Сколько для этого понадобится краски, если расходовать по 150 г на 1 м²?
Ответ:

1) 8 − 2 = 6 (м) – ширина комнаты.
2) 6 ∙ 8 = 48 (м²) – площадь комнаты.
3) 150 ∙ 48 = 7200 (г) – 7 кг 200 г – краски понадобится, чтобы покрасить пол в комнате.
Ответ: 7 кг 200 г краски всего понадобится для покраски пола в комнате
Повтори единицы массы – грамм и килограмм, единицу длины – метр, единицы площади, а также как найти площадь прямоугольника.
Оформляем условие в виде краткой записи.

Рассуждаем.
Найдем ширину комнаты.
1) 8 − 2 = 6 (м) – ширина комнаты.
Продолжаем рассуждение.
Вычислим площадь комнаты.
2) 6 ∙ 8 = 48 (м²) – площадь комнаты.
Продолжаем рассуждение.
Вычислим, сколько краски понадобится, чтобы покрасить пол в комнате.
3) 48 ∙ 150 = 7200 (г) – 7 кг 200 г – краски понадобится, чтобы покрасить пол в комнате.
Записываем ответ.
Ответ: 7 кг 200 г.
Номер 31.
Для спортивной школы купили 96 пар лыж по а р. за пару и 84 пары коньков по с р. Объясни, что обозначают выражения:
Ответ:
Лыжи - 96 пар по а р.
Коньки - 84 пары по с р.
1) а ∙ 96 – стоимость всех лыж.
2) с ∙ 84 – стоимость всех коньков.
3) а ∙ 96 + с ∙ 84 – стоимость всей покупки.
Повтори, что такое буквенные выражения, а также взаимосвязь между ценой, количеством и стоимостью.
Оформляем условие в виде краткой записи.
Лыжи – 96 пар по а р.
Коньки – 84 пары по с р.
Объясним, что обозначают выражения.
1) а ∙ 96 – стоимость всех лыж.
2) с ∙ 84 – стоимость всех коньков.
3) а ∙ 96 + с ∙ 84 – стоимость всей покупки.
Номер 32.
Проверь, верны ли неравенства.
Ответ:
2 т < 200 ц
2 т = 20 ц
20 ц < 200 ц
Значит, 2 т < 200 ц – верно
3 ц > 300 кг
3 ц = 300 кг
300 кг = 300 кг
Значит, 3 ц > 300 кг – неверно
2 сут. > 50 ч
2 сут. = 48 ч
48 ч < 50 ч
Значит, 2 сут. > 50 ч – неверно
3 года < 40 мес.
3 года = 36 мес.
36 мес. < 40 мес.
Значит, 3 года < 40 мес. – верно
2 км² > 2000 м²
2 км² = 2000000 м²
2000000 м2 > 2000 м²
Значит, 2 км² > 2000 м² – верно
5 м² < 100 дм²
5 м² = 500 дм²
500 дм² > 100 дм²
Значит, 5 м² < 100 дм²– неверно
Повтори единицы массы – тонну, центнер и килограмм, единицы времени – год, месяц, сутки и час, единицы площади, а также что такое неравенства.
Проверим, верны ли равенства.
2 т < 200 ц
2 т = 20 ц
20 ц < 200 ц
Значит, 2 т < 200 ц – верно
3 ц > 300 кг
3 ц = 300 кг
300 кг = 300 кг
Значит, 3 ц > 300 кг – неверно
2 сут. > 50 ч
2 сут. = 48 ч
48 ч < 50 ч
Значит, 2 сут. > 50 ч – неверно
3 года < 40 мес.
3 года = 36 мес.
36 мес. < 40 мес.
Значит, 3 года < 40 мес. – верно
2 км² > 2000 м²
2 км² = 2000000 м²
2000000 м² > 2000 м²
Значит, 2 км² > 2000 м² – верно
5 м² < 100 дм²
5 м² = 500 дм²
500 дм² > 100 дм²
Значит, 5 м² < 100 дм² – неверно
Оформим задание в тетрадь.
2 т < 200 ц – верно
3 ц > 300 кг – неверно
2 сут. > 50 ч – неверно
3 года < 40 мес. – верно
2 км² > 2 000 м² – верно
5 м² < 100 дм² – неверно
Номер 33.
Реши уравнения.
Ответ:
Повтори, как решать уравнения.
Выполняем вычисления.
387 : х = 513 : 57
387 : х = 9
х = 387 : 9
х = 43
Ответ: х = 43
у : 6 = 54 ∙ 8
у : 6 = 432
у = 432 ∙ 6
у = 2 592
Ответ: у = 2 592
3 210 – х = 665 : 7
3 210 – х = 95
х = 3 210 – 95
х = 3 115
Ответ: х = 3 115
Оформим задание в тетрадь.
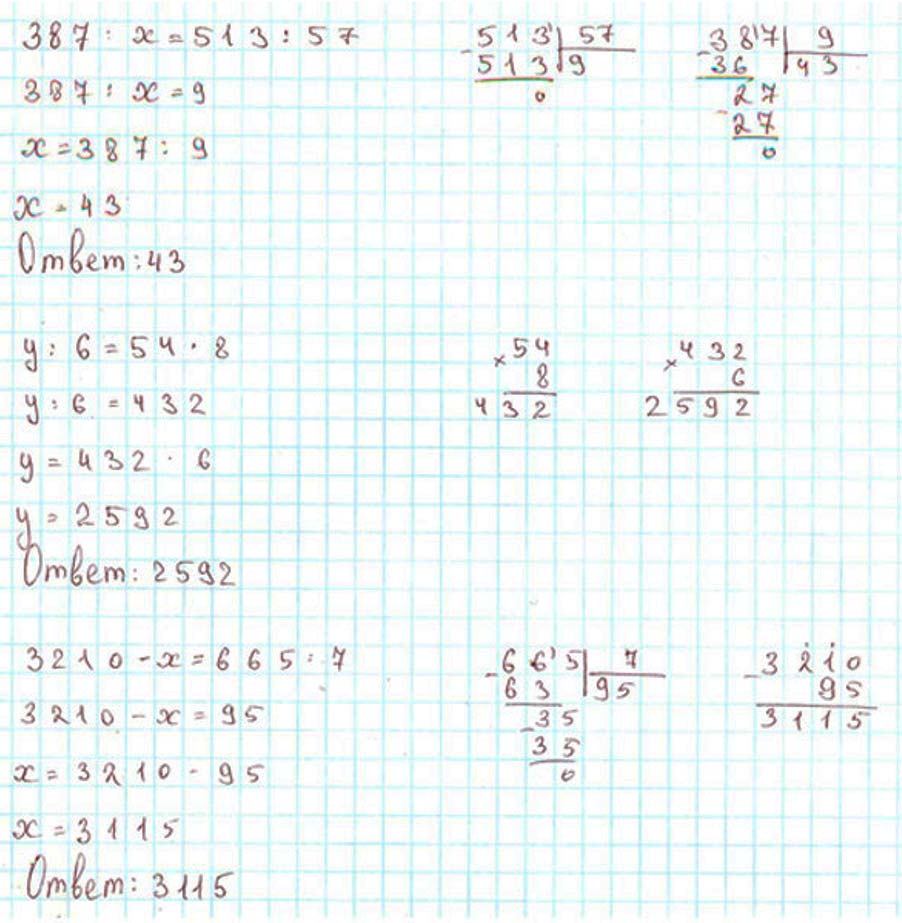
Номер 34.
1) Во сколько раз сумма чисел 933 и 1167 больше частного чисел 21600 и 72?
2) На сколько произведение чисел 725 и 30 больше разности этих чисел?

Повтори алгоритм письменного сложения, умножения и деления многозначных чисел, порядок действий, а также как называются числа при сложении, вычитании, умножении и делении.
Выполняем вычисления.
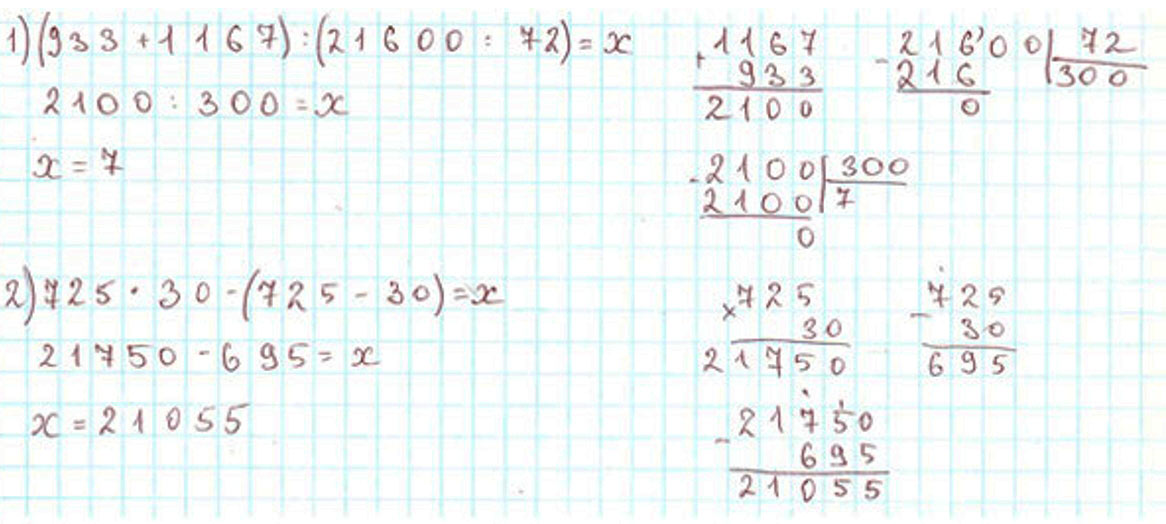
Оформим задание в тетрадь.
1) В 7 раз.
2) На 21 055.
Номер 35.
Сейчас 20 ч 48 мин. Сколько времени осталось до конца суток? На сколько больше прошедшая часть суток, чем оставшаяся?
Ответ:
Сутки = 24 ч 1) 24 ч − 20 ч 48 мин = 23 ч 60 мин − 20 ч 48 мин = 3 ч 12 мин − осталось до конца суток. 2) 20 ч 48 мин − 3 ч 12 мин = на 17 ч 36 мин − прошедшая часть суток, больше, чем оставшаяся.
Повтори единицы времени – час, минуту и сутки.
Оформляем условие в виде краткой записи.

Рассуждаем.
Узнаем, сколько времени составляет оставшаяся часть суток.
Сутки = 24 ч
1) 24 ч − 20 ч 48 мин = 23 ч 60 мин − 20 ч 48 мин = 3 ч 12 мин − осталось до конца суток.
Продолжаем рассуждение.
Узнаем, на сколько прошедшая часть суток, больше, чем оставшаяся.
2) 20 ч 48 мин − 3 ч 12 мин = на 17 ч 36 мин − прошедшая часть суток, больше, чем оставшаяся.
Номер 36.
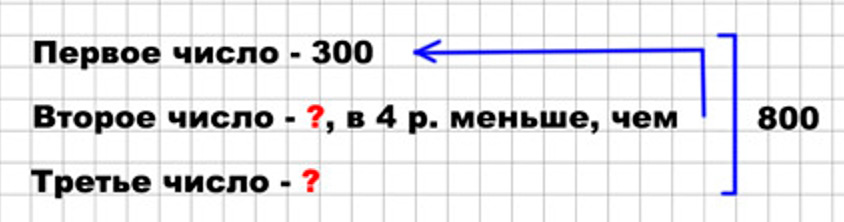
Сумма трёх чисел 800, первое число 300, оно в 4 раза больше второго числа. Найди третье число.
Ответ:
1) 300 : 4 = 75 – второе число.
2) 300 + 75 = 375 – сумма первого и второго числа.
3) 800 − 375 = 425 – третье число.
Ответ: третье число равно 425.
Повтори алгоритм письменного вычитания и деления трёхзначных чисел, а также как называются числа при сложении.
Оформляем условие в виде краткой записи.
Рассуждаем.
Узнаем, чему равно второе число.
1) 300 : 4 = 75 – второе число.
Продолжаем рассуждение.
Узнаем, чему равна сумма первого и второго числа.
2) 300 + 75 = 375 – сумма первого и второго числа.
Продолжаем рассуждение.
Узнаем, чему равно третье число.
3) 800 − 375 = 425 – третье число.
Записываем ответ.
Ответ: 425.
Номер 37.
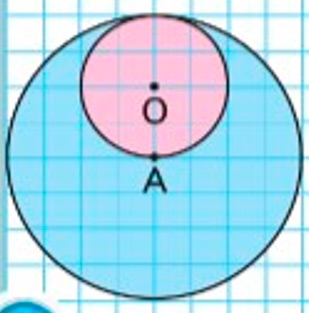
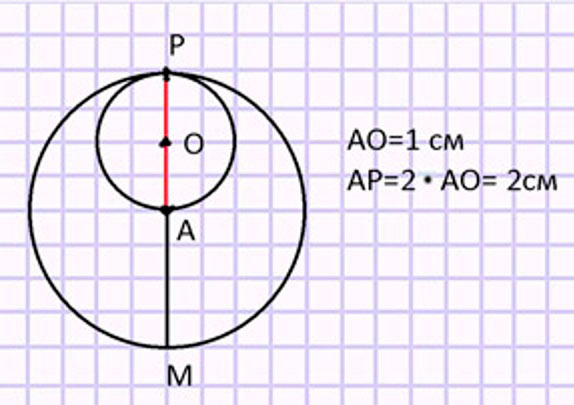
Рассмотри чертёж. Узнай длину диаметра большего круга, если радиус меньшего круга равен 1 см.

Ответ:

Радиус - отрезок, соединяющий центр окружности с точкой, на окружности. Все радиусы равны.
Радиус малого круга = 1 см = ОА.
Сумма двух радиусов равняется диаметру. Если мы продолжим отрезок АО по прямой, то получим отрезок АР, который является диаметром малого круга и радиусом большого круга.
А чтобы найти диаметр большого круга, нужно радиус большого круга умножить на 2, т.е. РМ = 2 см ∙ 2 = 4 см.
Ответ: диаметр большего круга составляет 4 см.
Повтори, что такое радиус и диаметр окружности.
Рассмотрим чертеж на полях страницы.
Рассуждаем.
Радиус – отрезок, соединяющий центр окружности с точкой, на окружности. Все радиусы равны.
Радиус малого круга = 1 см = ОА.
Сумма двух радиусов равняется диаметру. Если мы продолжим отрезок АО по прямой, то получим отрезок АР, который является диаметром малого круга и радиусом большого круга.
А чтобы найти диаметр большого круга, нужно радиус большого круга умножить на 2, т.е. РМ = 2 см ∙ 2 = 4 см.
Ответ: 4 см.
Оформляем задание в тетрадь.
Номер 10.
В четырёх ящиках всего 86 кг яблок; в первом и во втором поровну, в третьем 20 кг, а в четвертом 18 кг. Узнай, сколько килограммов яблок было в первом ящике.
Объясни, что обозначают следующие выражения, считая, что цена 1 кг яблок k р.:
1) k ∙ 20;
2) k ∙ (20 + 18);
3) k ∙ 86.

1) 86 − (20 + 18) = 48 (кг) – яблок в 1 и 2 ящиках.
2) 48 : 2 = 24 (кг) – яблок в первом ящике.
Ответ: 24 кг яблок в первом ящике всего.
1) к ∙ 20 – цена яблок в третьем ящике.
2) к ∙ (20 + 18) – цена яблок в третьем и четвертом ящиках.
3) к ∙ 86 – цена яблок во всех ящиках.
Номер 11.
Электропоезд отправился из города в 9 ч 15 мин и прибыл на конечную станцию в 10 ч 12 мин. По пути он делал остановку на каждой из 12 промежуточных станций в среднем на 35 с. Сколько времени электропоезд находился в движении от города до конечной станции? С какой скоростью он двигался, если известно, что расстояние от города до конечной станции 48 км?
Ответ:
Был в пути – с 9 ч 15 мин до 10 ч 12 мин
Остановки – 12 раз по 35 с
Расстояние – 48 км
Время в пути – ? ч
Скорость – ? м/мин
1) 12 ∙ 35 = 420 (с) = 7 мин – время остановок электропоезда.
2) 10 ч 12 мин − 9 ч 15 мин − 7 мин = 57 (мин) – время электропоезда в пути с остановками.
3) 57 − 7 = 50 (мин) - ехал поезд без остановок.
48 км = 48000 м
4) 48000 : 50 = 960 (м/мин) – скорость электропоезда.
Ответ: скорость электропоезда – 960 м/мин, а время в пути – 50 минут.
Номер 12.
Найди значения выражений удобным способом.
Ответ:
(115 + 85) ∙ 9 = 200 ∙ 9 = 1800
(500 + 45) : 5 = 500 : 5 + 45 : 5 = 100 + 9 = 109
(640 + 60) ∙ 7 = 700 ∙ 7 = 4900
(184 + 116) : 3 = 300 : 3 = 100
(670 + 30 ) ∙ 6 = 700 ∙ 6 = 4200
(720 + 80) : 8 = 800 : 8 = 100
Номер 13.
Вставь пропущенные числа.
Ответ:
7 т = 7000 кг
7 т = 70 ц
8 км = 8000 м
8 км = 80 000 дм
6 км² = 6000000 м²
6 м² = 600 дм²
Номер 14.
Объясни, почему значения выражений, записанных в каждом столбике, равны, а затем проверь вычислениями.
Ответ:
(1 728 + 4 482) : 54 = 1 728 : 54 + 4 482 : 54 – чтобы разделить сумму на число можно вначале сложить числа, а потом разделить на число или каждое слагаемое разделить на число, а потом полученные результаты сложить.
702 · (69 + 18) = 702 · 69 + 702 · 18 - чтобы умножить сумму на число можно вначале сложить числа, а потом умножить на число или каждое слагаемое умножить на число, а потом полученные результаты сложить.
Номер 15.
Найди значения выражений 3600 : b и 3600 ∙ b, если b = 48; b = 24; b = 15; b = 10; b = 5.
Ответ:
Номер 16.
Ответ:
Номер 17.
На чемпионате школы по игре в шахматы Лена сыграла 12 партий. Две партии она проиграла, а из остальных на каждые 2 партии вничью у неё 3 выигранные. Сколько шахматных побед у Лены?
Ответ:
Метод подбора:
Было сыграно партий – 12 штук
Проиграла – 2 штуки
Выиграла – ? на каждые 2 вничью 3 выигранные
Вничью – ? штук
1) 12 − 2 = 10 партий Лена не проиграла.
Партий сыгранных вничью должно быть хотя бы две, ведь иначе не будет выполняться второе условие.
Предположим, что партий сыгранных вничью – 2 штуки, значит выигранных 3 штуки.
Проверим: 2 + 2 + 3 = 7, а должно быть 12 штук. Значит партий сыгранных вничью не 2.
Предположим, что партий сыгранных вничью 4. Тогда партий выигранных – 8 штук.
2 + 4 + 8 = 14 такой вариант подходит.
Проверим еще один вариант.
Если партий сыгранных вничью – 6 штук, тогда выигранных – 18, что противоречит первому условию.
Значит партий выигранных – 6 штук.
Ответ: 6 штук.
Метод вычислений:
Было сыграно партий – 12 штук
Проиграла – 2 штуки
Выиграла – ? на каждые 2 вничью 3 выигранные
Вничью – ? штук
1) 12 − 2 = 10 партий Лена не проиграла.
2) 2 + 3 = 5 партий, из которых 2 лена сыграла вничью, а 3 выиграла.
3) 10 : 5 = 2 – дважды комбинация из 2) повторилась, значит было выиграно партий.
4) 2 ∙ 3 = 6 партий Лена выиграла.
Задание на полях страницы
Продолжи.

180 : 90 + 99 = 2 + 99 = 101 270 : 90 + 89 = 3 + 89 = 92 360 : 90 + 79 = 4 + 79 = 84 450 : 90 + 69 = 5 + 69 = 74 540 : 90 + 59 = 6 + 59 = 64 630 : 90 + 49 = 7 + 49 = 56 720 : 90 + 39 = 8 + 39 = 47
Ребус.


С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.