Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 83

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 10.
В четырёх ящиках всего 86 кг яблок; в первом и во втором поровну, в третьем 20 кг, а в четвертом 18 кг. Узнай, сколько килограммов яблок было в первом ящике.
Объясни, что обозначают следующие выражения, считая, что цена 1 кг яблок k р.:
1) k ∙ 20;
2) k ∙ (20 + 18);
3) k ∙ 86.

1) 86 − (20 + 18) = 48 (кг) – яблок в 1 и 2 ящиках.
2) 48 : 2 = 24 (кг) – яблок в первом ящике.
Ответ: 24 кг яблок всего в первом ящике.
1) к ∙ 20 – цена яблок в третьем ящике.
2) к ∙ (20 + 18) – цена яблок в третьем и четвертом ящиках.
3) к ∙ 86 – цена яблок во всех ящиках.
Повтори способы оформления краткой записи к задаче, единицу массы – килограмм, а также что такое буквенные выражения.
Оформляем условие в виде краткой записи.
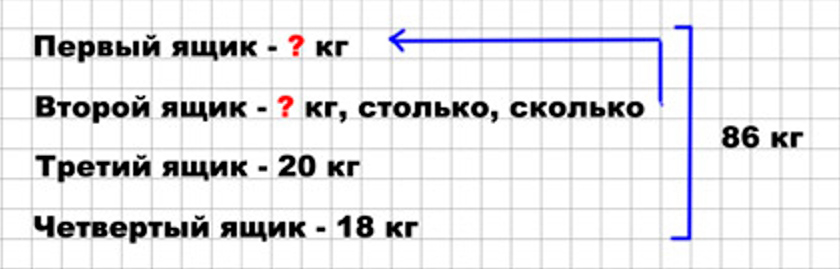
Рассуждаем.
Узнаем, сколько яблок в первом и втором ящиках вместе.
1) 86 − (20 + 18) = 48 (кг) – яблок в 1 и 2 ящиках.
Продолжаем рассуждение.
Узнаем, сколько яблок в первом ящике.
2) 48 : 2 = 24 (кг)
Записываем ответ.
Ответ: 24 кг яблок в первом ящике.
Объясним, что обозначают выражения.
1) к ∙ 20 – цена яблок в третьем ящике.
2) к ∙ (20 + 18) – цена яблок в третьем и четвертом ящиках.
3) к ∙ 86 – цена яблок во всех ящиках.
Номер 11.
Электропоезд отправился из города в 9 ч 15 мин и прибыл на конечную станцию в 10 ч 12 мин. По пути он делал остановку на каждой из 12 промежуточных станций в среднем на 35 с. Сколько времени электропоезд находился в движении от города до конечной станции? С какой скоростью он двигался, если известно, что расстояние от города до конечной станции 48 км? (Вырази расстояние в метрах, а время в минутах.)
Ответ:
Был в пути – с 9 ч 15 мин до 10 ч 12 мин
Остановки – 12 раз по 35 с
Расстояние – 48 км
Время в пути – ? ч
Скорость – ? м/мин
1) 12 ∙ 35 = 420 (с) = 7 мин – время остановок электропоезда.
2) 10 ч 12 мин − 9 ч 15 мин = 57 (мин) – время электропоезда в пути с остановками.
3) 57 − 7 = 50 (мин) - ехал поезд без остановок.
48 км = 48000 м
4) 48000 : 50 = 960 (м/мин) – скорость электропоезда.
Ответ: скорость электропоезда – 960 м/мин, а время в пути – 50 минут.
Повтори единицы времени – час и минуту, а также взаимосвязь между скоростью, временем и расстоянием.
Оформляем условие в виде краткой записи.
Был в пути – с 9 ч 15 мин до 10 ч 12 мин
Остановки – 12 раз по 35 с
Расстояние – 48 км
Время в пути – ? ч
Скорость – ? м/мин
Рассуждаем.
Узнаем, сколько времени заняли у электропоезда остановки.
1) 12 ∙ 35 = 420 (с) = 7 мин – время остановок электропоезда.
Продолжаем рассуждение.
Узнаем, сколько времени занял путь электропоезда с остановками.
2) 10 ч 12 мин − 9 ч 15 мин − 7 мин = 57 (мин) – время электропоезда в пути с остановками.
Продолжаем рассуждение.
Узнаем, сколько времени занял путь электропоезда без остановок.
3) 57 − 7 = 50 (мин) – ехал поезд без остановок.
48 км = 48000 м
Продолжаем рассуждение.
Узнаем, с какой скоростью двигался электропоезд.
4) 48000 : 50 = 960 (м/мин) – скорость электропоезда.
Записываем ответ.
Ответ: скорость электропоезда – 960 м/мин, а время в пути – 50 минут.
Номер 12.
Найди значения выражений удобным способом.
Ответ:
(115 + 85) ∙ 9 = 200 ∙ 9 = 1800
(500 + 45) : 5 = 500 : 5 + 45 : 5 = 100 + 9 = 109
(640 + 60) ∙ 7 = 700 ∙ 7 = 4900
(184 + 116) : 3 = 300 : 3 = 100
(670 + 30 ) ∙ 6 = 700 ∙ 6 = 4200
(720 + 80) : 8 = 800 : 8 = 100
Повтори свойства умножения.
Выполняем вычисления.
(115 + 85) ∙ 9 = 200 ∙ 9 = 1800
(500 + 45) : 5 = 500 : 5 + 45 : 5 = 100 + 9 = 109
(640 + 60) ∙ 7 = 700 ∙ 7 = 4900
(184 + 116) : 3 = 300 : 3 = 100
(670 + 30) ∙ 6 = 700 ∙ 6 = 4200
(720 + 80) : 8 = 800 : 8 = 100
Оформляем задание в тетрадь.
(115 + 85) ∙ 9 = 1 800
(500 + 45) : 5 = 109
(640 + 60) ∙ 7 = 4 900
(184 + 116) : 3 = 100
(670 + 30) ∙ 6 = 4 200
(720 + 80) : 8 = 100
Номер 13.
Вставь пропущенные числа.
Ответ:
7 т = 7000 кг
7 т = 70 ц
8 км = 8000 м
8 км = 80 000 дм
6 км² = 6000000 м²
6 м² = 600 дм²
Повтори единицы массы – тонну, центнер и килограмм, единицы длины – километр, метр и дециметр, а также единицы площади.
Выполняем вычисления с пояснениями.
1 т = 1 000 кг, поэтому 7 т = 7 ∙ 1 000 = 7 000 кг.
1 т = 10 ц, поэтому 7 т = 7 ∙ 10 = 70 ц.
1 км = 1 000 м, поэтому 8 км = 8 ∙ 1 000 = 8 000 м.
1 км = 10 000 дм, поэтому 8 км = 8 ∙ 10 000 = 80 000 дм.
1 км² = 1 000 000 м², поэтому 6 км² = 6 ∙ 1 000 000 = 6 000 000 м².
1 м² = 100 дм², поэтому 6 м² = 6 ∙ 100 = 600 дм².
Оформляем задание в тетрадь.
7 т = 7000 кг
7 т = 70 ц
8 км = 8000 м
8 км = 80 000 дм
6 км² = 6000000 м²
6 м² = 600 дм²
Номер 14.
Вычисли и объясни, почему значения выражений, записанных в каждом столбике, равны.
Ответ:
Повтори свойства умножения и деления.
Рассуждаем.
В первом случае используется распределительный закон деления:
(1728 + 4482) : 54=1728 : 54 + 4482 : 54
Во втором случае используется распределительный закон умножения:
702 ∙ (69 + 18) = 702 ∙ 69 + 702 ∙ 18
Выполняем вычисления и оформляем задание в тетрадь.
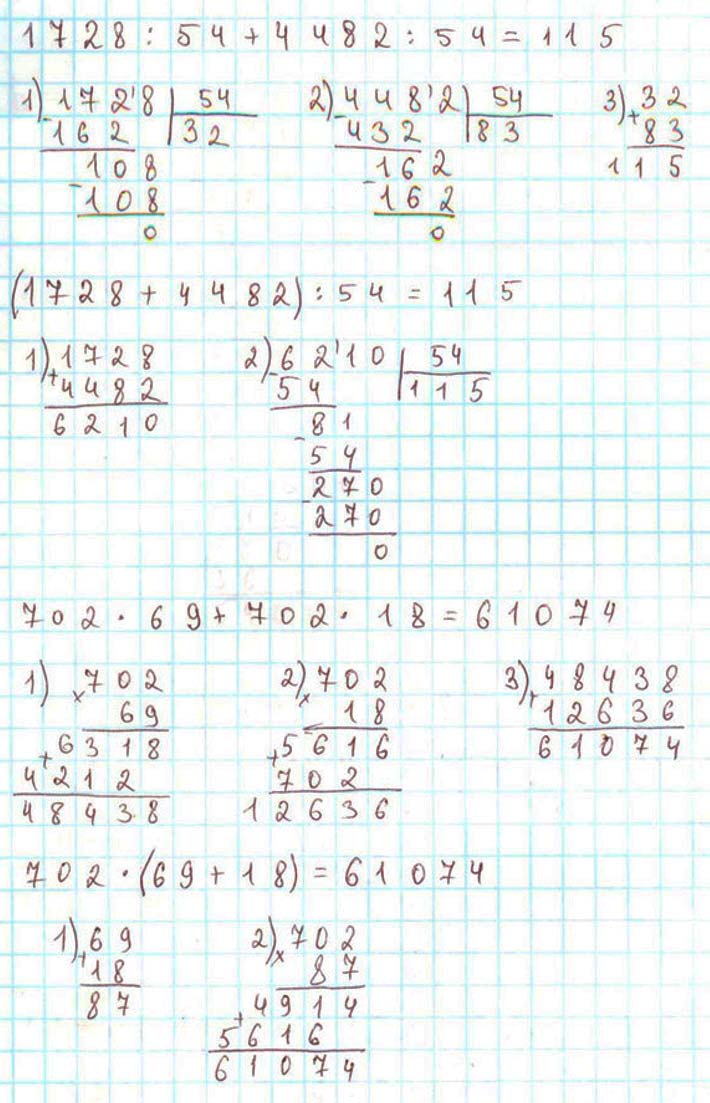
Номер 15.
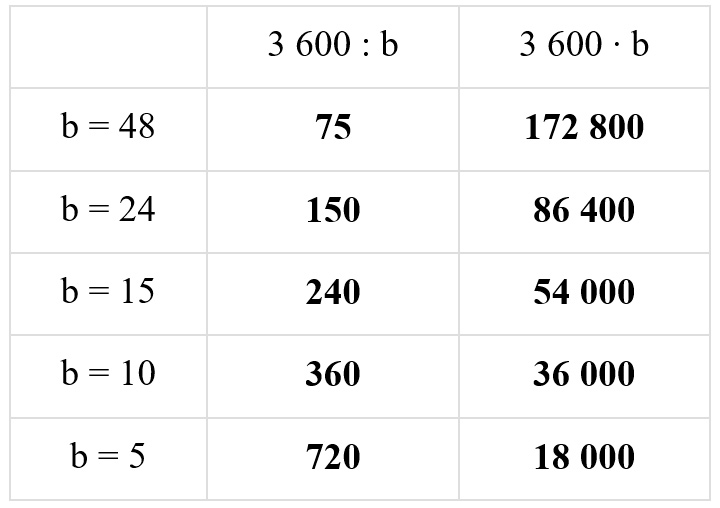
Найди значения выражений 3600 : b и 3600 ∙ b, если b = 48; b = 24; b = 15; b = 10; b = 5.
Ответ:
Повтори, что такое буквенные выражения.
Выполняем вычисления.

Оформляем задание в тетрадь.
Номер 16.
Ответ:
Повтори алгоритм письменного умножения и деления многозначных чисел, а также порядок действий.
Выполняем вычисления с пояснениями.

3) 10 + 1 190 = 1 200
4) 10 000 – 1 200 = 8 800

3) 840 – 640 = 200
4) 12 000 : 200 = 60
Рассуждаем.
Нужно разделить 67 068 : 324. Выделю первое неполное делимое – 670. Чтобы легче было найти цифру частного, разделим 670 на 300.
Для этого разделим 67 на 3, в частном получим 2.
Это пробная цифра, её нужно проверить.
Умножим 324 на 2, получится 648.
670 – 648 = 22. Добавим 6 дес.
Нахожу вторую цифру частного:
226 : 324.
226 меньше, чем 324, пишу в частном 0. Добавляю 8 ед.
Нахожу третью цифру частного:
2 268 : 324, получу 7.
Умножу 324 на 7, получу 2 268.
2 268 – 2 268 = 0.
Частное 207.
Нужно разделить 226 720 : 436. Выделю первое неполное делимое – 2 276. Чтобы легче было найти цифру частного, разделим 2 267 на 400.
Для этого разделим 22 на 4, в частном получим 5.
Это пробная цифра, её нужно проверить.
Умножим 436 на 5, получится 2 180.
2 267 – 2 180 = 87. Добавим 2 дес.
Нахожу вторую цифру частного:
872 : 436, получу 2.
Умножу 436 на 2, получу 872.
872 – 872 = 0.
Нахожу третью цифру частного:
0 : 436, получу 0.
Частное 520.
Оформляем задание в тетрадь.
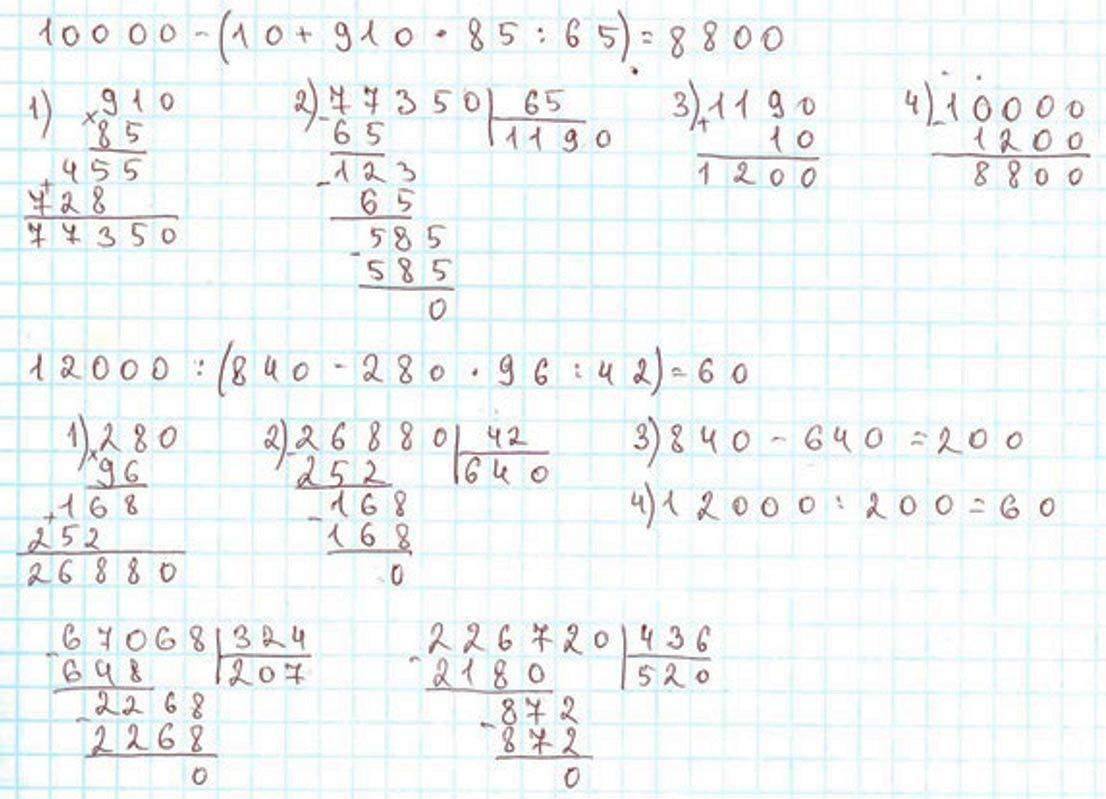
Номер 17.
На чемпионате школы по игре в шахматы Лена сыграла 12 партий. Две партии она проиграла, а из остальных на каждые 2 партии вничью у неё 3 выигранные. Сколько шахматных побед у Лены?
Ответ:
Метод подбора:
Было сыграно партий – 12 штук
Проиграла – 2 штуки
Выиграла – ? на каждые 2 вничью 3 выигранные
Вничью – ? штук
1) 12 − 2 = 10 партий Лена не проиграла.
Партий сыгранных вничью должно быть хотя бы две, ведь иначе не будет выполняться второе условие.
Предположим, что партий сыгранных вничью – 2 штуки, значит выигранных 3 штуки.
Проверим: 2 + 2 + 3 = 7, а должно быть 12 штук. Значит партий сыгранных вничью не 2.
Предположим, что партий сыгранных вничью 4. Тогда партий выигранных – 8 штук.
2 + 4 + 8 = 14 такой вариант подходит.
Проверим еще один вариант.
Если партий сыгранных вничью – 6 штук, тогда выигранных – 18, что противоречит первому условию.
Значит партий выигранных – 6 штук.
Ответ: 6 штук шахматных побед у Лены.
Метод вычислений:
Было сыграно партий – 12 штук
Проиграла – 2 штуки
Выиграла – ? на каждые 2 вничью 3 выигранные
Вничью – ? штук
1) 12 − 2 = 10 партий Лена не проиграла.
2) 2 + 3 = 5 партий, из которых 2 Лена сыграла вничью, а 3 выиграла.
3) 10 : 5 = 2 – дважды комбинация из 2) повторилась, значит было выиграно партий.
4) 2 ∙ 3 = 6 партий Лена выиграла.
Повтори таблицу умножения.
Метод подбора.
Было сыграно партий – 12 штук
Проиграла – 2 штуки
Выиграла – ? на каждые 2 вничью 3 выигранные
Вничью – ? штук
12 − 2 = 10 партий Лена не проиграла.
Партий сыгранных вничью должно быть хотя бы две, ведь иначе не будет выполняться второе условие.
Предположим, что партий сыгранных вничью – 2 штуки, значит выигранных 3 штуки.
Проверим: 2 + 2 + 3 = 7, а должно быть 12 штук. Значит партий сыгранных вничью не 2.
Предположим, что партий сыгранных вничью 4. Тогда партий выигранных – 8 штук.
2 + 4 + 8 = 14 такой вариант подходит.
Проверим еще один вариант.
Если партий сыгранных вничью – 6 штук, тогда выигранных – 18, что противоречит первому условию.
Значит партий выигранных – 6 штук.
Ответ: 6 штук.
Метод вычислений.
Было сыграно партий – 12 штук
Проиграла – 2 штуки
Выиграла – ? на каждые 2 вничью 3 выигранные
Вничью – ? штук
1) 12 − 2 = 10 партий Лена не проиграла.
2) 2 + 3 = 5 партий, из которых 2 лена сыграла вничью, а 3 выиграла.
3) 10 : 5 = 2 – дважды комбинация из 2) повторилась, значит было выиграно партий.
4) 2 ∙ 3 = 6 партий Лена выиграла.
Задание на полях страницы
Продолжи.

Ответ:
180 : 90 + 99 = 2 + 99 = 101 270 : 90 + 89 = 3 + 89 = 92 360 : 90 + 79 = 4 + 79 = 83 450 : 90 + 69 = 5 + 69 = 74 540 : 90 + 59 = 6 + 59 = 65 630 : 90 + 49 = 7 + 49 = 56 720 : 90 + 39 = 8 + 39 = 47
Повтори таблицу деления.
Выполняем вычисления с пояснением.
В каждой следующей строчке первое число на 90 больше, а третье – на 10 меньше.
180 : 90 + 99 = 2 + 99 = 101
270 : 90 + 89 = 3 + 89 = 92
360 : 90 + 79 = 4 + 79 = 83
450 : 90 + 69 = 5 + 69 = 74
540 : 90 + 59 = 6 + 59 = 65
630 : 90 + 49 = 7 + 49 = 56
720 : 90 + 39 = 8 + 39 = 47
Оформляем задание в тетрадь.
180 : 90 + 99 = 101
270 : 90 + 89 = 92
360 : 90 + 79 = 83
450 : 90 + 69 = 74
540 : 90 + 59 = 65
630 : 90 + 49 = 56
720 : 90 + 39 = 47
Ребус.

Ответ:

Перед нами ребус, для того чтобы найти недостающие цифры необходимо выполнить умножение.
Рассмотрим ребус.

Разгадаем ребус.
На какое однозначное число можно умножить 6, чтобы в единицах получилось 0? 0 или 5. 0 не подходит, так как другие числа будут равны нулю. Значит, это число 5.
Умнжаю единицы 6 ∙ 5 = 30. 3 дес. запомню и прибавлю к десяткам после умножения десятков.
После прибавления 3 дес. к десяткам в десятках записали 3. Значит, после умножения на 5 получилось 0 в единицах. Это число 2.
Умножаю десятки: 2 ∙ 5 = 10. 1 сот. Прибавлю к сотням.
Умножаю сотни: 2 ∙ 5 = 10. 10 + 1 = 11. Пишу 1 под сотнями и 1 под единицами тысяч.
Умножаю на второй множитель.
Умножаю единицы: 6 ∙ 2 = 12. Пишу 2 под десятками, 1 прибавлю к сотням.
Умножаю десятки: 2 ∙ 2 = 4. 4 + 1 = 5. Пишу 5 под сотнями.
Складываю единицы. Пишу 0 под единицами.
Складываю сотни: 1 + 5 = 6.
Оформим задание в тетрадь.
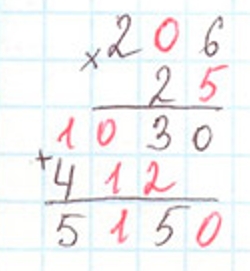
Номер 7.
Реши подбором. В коробке лежат синие, красные и жёлтые кубики – всего 20 кубиков. Синих кубиков в 6 раз больше, чем жёлтых. Красных кубиков меньше, чем синих. Сколько красных кубиков в коробке?
Ответ:
Предположим, что желтых кубиков 1, тогда синих 6, ведь их в шесть раз больше.
1 + 6 = 7 кубиков синих и желтых в коробке.
20 − 7 = 13 красных кубиков в коробке.
Такого быть не может, ведь по условию красных кубиков меньше, чем синих, а 13 > 6.
Предположим, что желтых кубиков 2, тогда синих 12, ведь их в 6 раз больше.
2 + 12 = 14 кубиков синих и желтых в коробке.
20 − 14 = 6 красных кубиков в коробке.
Такой вариант подходит, потому что выполняется второе условие, по которому красных кубиков меньше, чем синих.
6 < 12
Предположим, что желтых кубиков 3, тогда синих 18, ведь их в 6 раз больше.
3 + 18 = 21 кубиков синих и желтых в коробке.
Такого быть не может, ведь кубиков в коробке всего 20.
Значит, подходит только комбинация: 2 желтых кубика, 12 синих и 6 красных.
Ответ: значит в коробке 6 красных кубиков.
Номер 8.
За две книги заплатили 272 р. Цена одной книги составляет третью часть цены другой книги. Сколько стоит каждая книга?
Ответ:
Цена второй книги – третья часть от цены первой книги, значит цена первой книги в 3 раза больше цены второй.
Цена второй книги – х
Цена первой книги – х ∙ 3
Всего книги стоят 272 рубля
х + х ∙ 3 = 272
4х = 272
х = 68
68 рублей - цена второй книги.
68 ∙ 3 = 204 рубля – цена первой книги.
Ответ: цена второй книги составляет 68 рублей и цена первой книги составляет 204 рубля.
Номер 9.
Во время медосбора пчела вылетает из улья и летит к липе со скоростью 4 м/с, собирает нектар и возвращается в улей через 7 мин со скоростью 2 м/с. На каком расстоянии от улья находится липа, если на сбор нектара у пчелы уходит 1 мин?
Ответ:
1) 7 − 1 = 6 (мин) = 360 (с) – тратит пчела на дорогу.
2) 4 : 2 = в 2 (раза) – меньше скорость пчелы на обратном пути (обратный путь занимает в 2 раза больше времени, тогда примем весь путь за 3 части).
3) 360 : 3 = 120 (с) – летит пчела от улья к липе.
4) 120 ∙ 4 = 480 (м) – расстояние от улья до липы.
Ответ: расстояние от улья до липы составляет 480 м.
Номер 10.
Между некоторыми цифрами 1 2 3 4 5 поставь знаки арифметических действий и скобки так, чтобы получить новое числовое выражение, значение которого равно 40.
Ответ:(12 : 3 + 4) ∙ 5 = (4 + 4) ∙ 5 = 8 ∙ 5 = 40
Номер 11.
Начерти отрезок AD длиной 7 см. Отметь на нём точки В и С так, чтобы отрезок ВС был в 2 раза короче отрезка АВ и в 2 раза длиннее отрезка CD.
Ответ:
Если отрезок CD равен х см, то отрезок BC равен 2х см, ведь он в 2 раза длиннее.
Отрезок АВ = 4х см, ведь BC в 2 раза короче АВ.
Причем в сумме отрезки равны 7 см.
Получается, х + 2х + 4х = 7
7х = 7
х = 1 см
Длина отрезка CD = 1 см.
Длина отрезка BC = 2 см.
Длина отрезка АВ = 4 см.
Ответ: длина отрезка CD составляет 1 см, длина отрезка ВС составляет 2 см и длина отрезка АВ составляет 4 см.
Номер 12.
Периметр одного прямоугольника равен 20 см, а другого – 22 см. Площадь каждого из этих многоугольников 24 см². Начерти в тетради эти прямоугольники.
Ответ:
Р 1 = 20 см
Р 2 = 22 см
S 1, 2 = 24 см²
1) 20 : 2 = 10 (см) – сумма сторон первого прямоугольника.
2) 22 : 2 = 11 (см) – сумма длин второго прямоугольника.
S = длина ∙ ширина
24 =
1) 1 ∙ 24
2) 2 ∙ 12
3) 3 ∙ 8
4) 4 ∙ 6
Нужно выбрать такие комбинации сторон, чтобы в сумме было 10 и 11.
Это комбинации 3 и 8, 4 и 6.
Значит, стороны первого прямоугольника 4 и 6 см, а второго – 3 см и 8 см.

Номер 13.
Начерти окружность любого радиуса. Не выполняя измерений, проведи внутри окружности 2 равных отрезка. Покажи два решения.
Ответ:
Номер 14.
Восстанови пропущенные числа.


С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.