Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 81
- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
.jpg "Математика 4 класс Моро, Волкова - 2 часть страница 81")
Номер 7.
Реши подбором. В коробке лежат синие, красные и жёлтые кубики – всего 20 кубиков. Синих кубиков в 6 раз больше, чем жёлтых. Красных кубиков меньше, чем синих. Сколько красных кубиков в коробке?
Ответ:
Предположим, что желтых кубиков 1, тогда синих 6, ведь их в шесть раз больше.
1 + 6 = 7 кубиков синих и желтых в коробке.
20 − 7 = 13 красных кубиков в коробке.
Такого быть не может, ведь по условию красных кубиков меньше, чем синих, а 13 > 6.
Предположим, что желтых кубиков 2, тогда синих 12, ведь их в 6 раз больше.
2 + 12 = 14 кубиков синих и желтых в коробке.
20 − 14 = 6 красных кубиков в коробке.
Такой вариант подходит, потому что выполняется второе условие, по которому красных кубиков меньше, чем синих.
6 < 12
Предположим, что желтых кубиков 3, тогда синих 18, ведь их в 6 раз больше.
3 + 18 = 21 кубиков синих и желтых в коробке.
Такого быть не может, ведь кубиков в коробке всего 20.
Значит, подходит только комбинация: 2 желтых кубика, 12 синих и 6 красных.
Ответ: значит в коробке 6 красных кубиков.
Повтори случаи табличного умножения и что такое неравенства.
Оформляем условие в виде краткой записи.
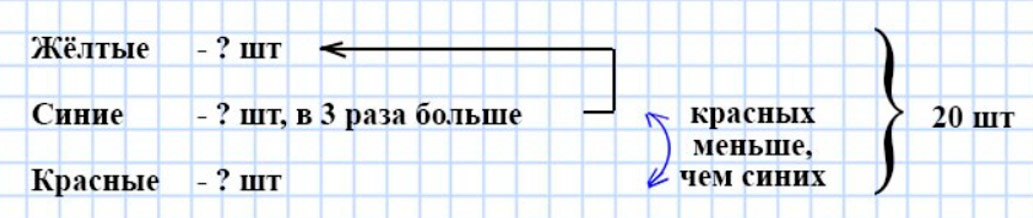
Рассуждаем.
Предположим, что желтых кубиков 1, тогда синих 6, ведь их в шесть раз больше.
1 + 6 = 7 кубиков синих и желтых в коробке.
20 − 7 = 13 красных кубиков в коробке.
Такого быть не может, ведь по условию красных кубиков меньше, чем синих, а 13 > 6.
Предположим, что желтых кубиков 2, тогда синих 12, ведь их в 6 раз больше.
2 + 12 = 14 кубиков синих и желтых в коробке.
20 − 14 = 6 красных кубиков в коробке.
Такой вариант подходит, потому что выполняется второе условие, по которому красных кубиков меньше, чем синих.
6 < 12
Предположим, что желтых кубиков 3, тогда синих 18, ведь их в 6 раз больше.
3 + 18 = 21 кубиков синих и желтых в коробке.
Такого быть не может, ведь кубиков в коробке всего 20.
Значит, подходит только комбинация: 2 желтых кубика, 12 синих и 6 красных.
Записываем ответ.
Ответ: значит в коробке 6 красных кубиков.
Оформляем задание в тетрадь.
Номер 8.
За две книги заплатили 272 р. Цена одной книги составляет третью часть цены другой книги. Сколько стоит каждая книга?
Ответ:
Цена второй книги - третья часть от цены первой книги, значит цена первой книги в 3 раза больше цены второй.
Цена второй книги - х
Цена первой книги - х ∙ 3
Всего книги стоят 272 рубля
х + х ∙ 3 = 272
4 ∙ х = 272
х = 68
68 рублей - цена второй книги.
68 ∙ 3 = 204 рубля - цена первой книги.
Ответ: цена второй книги составляет 68 рублей и цена первой книги составляет 204 рубля.
Повтори случаи вне табличного умножения и деления, а также что такое доли.
Оформляем условие в виде схематического чертежа.
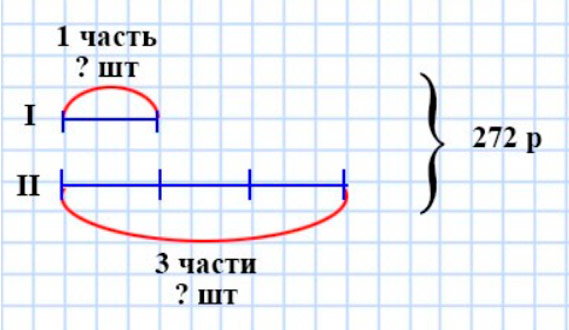
Рассуждаем.
Если цена одной книги – третья часть цены другой книги, значит цена другой книги в 3 раза больше. Значит, цена первой книги – одна часть, а цена второй книги – три таких части. Значит, стоимость двух книг нужно разделить на 4, чтобы узнать цену одной книги.
1) 272 : 4 = 68 (р.) – стоимость
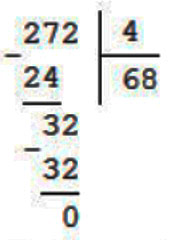
Продолжаем рассуждение.
Цена одной книги 68 рублей, цена другой книги – в 3 раза больше. Узнаем цену другой книги.
2) 68 ∙ 3 = 204 (р.)
Записываем ответ.
Ответ: 68 рублей и 204 рубля.
Номер 9.
Во время медосбора пчела вылетает из улья и летит к липе со скоростью 4 м/с, собирает нектар и возвращается в улей через 7 мин со скоростью 2 м/с. На каком расстоянии от улья находится липа, если на сбор нектара у пчелы уходит 1 мин?
Ответ:
1) 7 − 1 = 6 (мин) = 360 (с) – тратит пчела на дорогу.
2) 4 : 2 = в 2 (раза) – меньше скорость пчелы на обратном пути (обратный путь занимает в 2 раза больше времени, тогда примем весь путь за 3 части).
3) 360 : 3 = 120 (с) – летит пчела от улья к липе.
4) 120 ∙ 4 = 480 (м) – расстояние от улья до липы.
Ответ: расстояние от улья до липы составляет 480 м.
Повтори взаимосвязь между скоростью, временем и расстоянием, а также что такое доли.
Оформляем условие в виде таблицы.
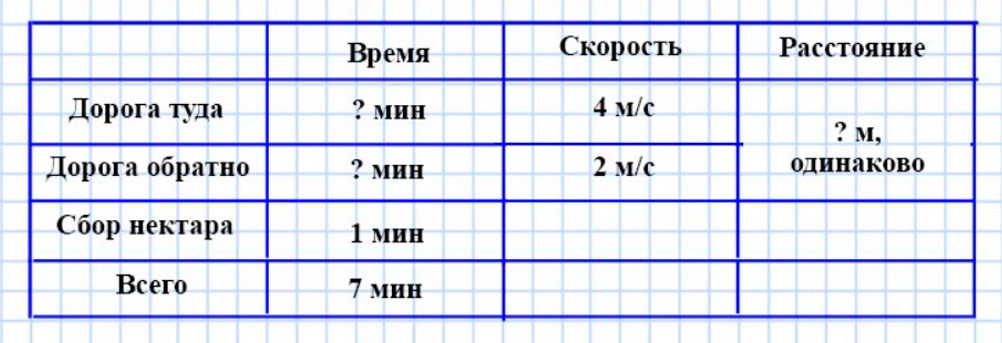
Рассуждаем.
Узнаем, сколько секунд пчела тратит на дорогу.
1) 7 − 1 = 6 (мин) = 360 (с) – тратит пчела на дорогу.
Продолжаем рассуждение.
Узнаем, во сколько раз меньше скорость пчелы на обратном пути.
2) 4 : 2 = в 2 (раза) – меньше скорость пчелы на обратном пути (обратный путь занимает в 2 раза больше времени, тогда примем весь путь за 3 части).
Продолжаем рассуждение.
Узнаем, сколько секунд пчела тратит на дорогу от улья к липе.
3) 360 : 3 = 120 (с) – летит пчела от улья к липе.
Продолжаем рассуждение.
Узнаем, какое расстояние от улья до липы.
4) 120 ∙ 4 = 480 (м)
Записываем ответ.
Ответ: 480 метров расстояние от улья до липы.
Номер 10.
Между некоторыми цифрами 1 2 3 4 5 поставь знаки арифметических действий и скобки так, чтобы получить новое числовое выражение, значение которого равно 40.
Ответ:(12 : 3 + 4) ∙ 5 = (4 + 4) ∙ 5 = 8 ∙ 5 = 40
Повтори случаи табличного умножения и деления, а также порядок действий.
Выполняем вычисления.
(12 : 3 + 4) ∙ 5 = (4 + 4) ∙ 5 = 8 ∙ 5 = 40
Оформляем задание в тетрадь.
Номер 11.
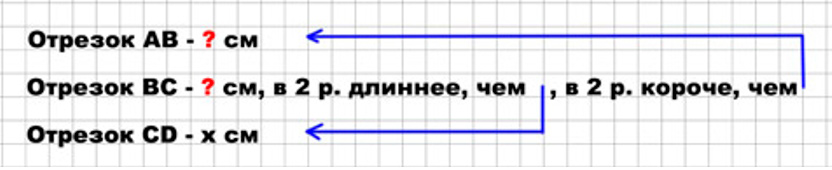
Начерти отрезок AD длиной 7 см. Отметь на нём точки В и С так, чтобы отрезок ВС был в 2 раза короче отрезка АВ и в 2 раза длиннее отрезка CD.
Ответ:
Если отрезок CD равен х см, то отрезок BC равен 2х см, ведь он в 2 раза длиннее.
Отрезок АВ = 4х см, ведь BC в 2 раза короче АВ.
Причем в сумме отрезки равны 7 см.
Получается, х + 2х + 4х = 7
7х = 7
х = 1 см
Длина отрезка CD = 1 см.
Длина отрезка BC = 2 см.
Длина отрезка АВ = 4 см.
Ответ: длина отрезка CD составляет 1 см, длина отрезка ВС составляет 2 см и длина отрезка АВ составляет 4 см.
Повтори, что такое отрезок, доли и единицу длины – сантиметр.
Оформляем условие в виде схематического чертежа.
Начертим отрезок.
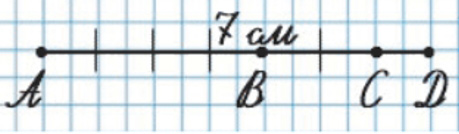
Рассуждаем.
Из условия задачи следует, что отрезок CD – самый маленький. Возьмем его за 1 часть. Значит, Отрезок ВС – 2 части, так как он больше отрезка СD в 2 раза. Отрезок АВ больше отрезка ВС в 2 раза, значит АВ – 4 части. Сложим все части.
4 + 2 + 1 = 7 (ч.)
Продолжаем рассуждение.
Вычислим, чему равна длина отрезка СD.
1) 7 : 7 = 1 (см.)
Вычислим, чему равна длина отрезка ВС.
2) 1 ∙ 2 = 2 (см.)
Вычислим, чему равна длина отрезка АВ.
3) 1 ∙ 4 = 4 (см.)
Записываем ответ.
Ответ: 1 см, 2 см и 4 см.
Номер 12.
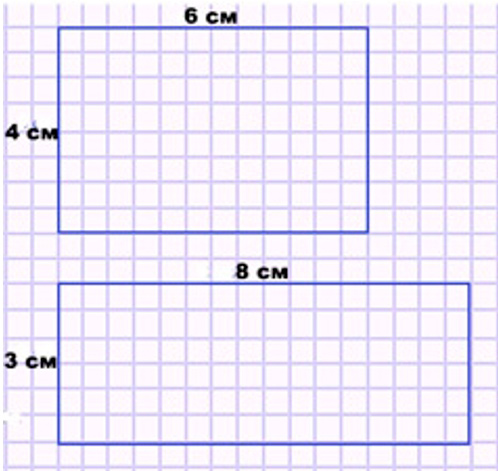
Периметр одного прямоугольника равен 20 см, а другого – 22 см. Площадь каждого из этих многоугольников 24 см². Начерти в тетради эти прямоугольники.
Ответ:
Р 1 = 20 см
Р 2 = 22 см
S 1, 2 = 24 см²
1) 20 : 2 = 10 (см) – сумма сторон первого прямоугольника.
2) 22 : 2 = 11 (см) – сумма длин второго прямоугольника.
S = длина ∙ ширина
24 =
1) 1 ∙ 24
2) 2 ∙ 12
3) 3 ∙ 8
4) 4 ∙ 6
Нужно выбрать такие комбинации сторон, чтобы в сумме было 10 и 11.
Это комбинации 3 и 8, 4 и 6.
Значит, стороны первого прямоугольника 4 и 6 см, а второго – 3 см и 8 см.
Повтори, как найти площадь и периметр прямоугольника, а также единицу длины – сантиметр.
Вычислим, чему равны длина и ширина прямоугольников.
Р1 = 20 см
Р2 = 22 см
S1, 2 = 24 см²
1) 20 : 2 = 10 (см) – сумма сторон первого прямоугольника.
2) 22 : 2 = 11 (см) – сумма длин второго прямоугольника.
S = длина ∙ ширина
24 =
1) 1 ∙ 24
2) 2 ∙ 12
3) 3 ∙ 8
4) 4 ∙ 6
Нужно выбрать такие комбинации сторон, чтобы в сумме было 10 и 11.
Это комбинации 3 и 8, 4 и 6.
Значит, стороны первого прямоугольника – 4 и 6 см, а второго – 3 см и 8 см.
Начертим прямоугольники.
Оформим задание в тетрадь.
Номер 13.
Начерти окружность любого радиуса. Не выполняя измерений, проведи внутри окружности 2 равных отрезка. Покажи два решения.
Ответ:
Повтори, что такое окружность, радиус и диаметр.
Чертим окружность и проводим внутри отрезки по данным задания.
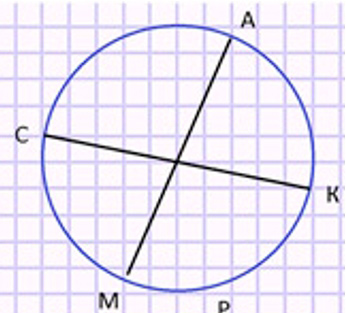
Первый вариант: можно провести два диаметра, ведь все диаметры окружности равны.
СК = АМ
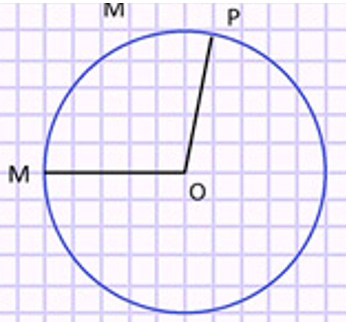
Второй вариант: можно провести два радиуса, ведь все радиусы окружности равны.
ОР = ОМ
Оформляем задание в тетрадь.
Номер 14.
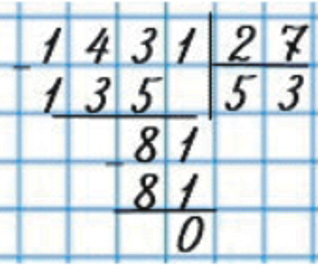
Восстанови пропущенные числа.
Ответ:
Повтори алгоритм письменного деления на двузначное число.
Восстанавливаем пропущенные числа.
Рассмотрим второе неполное делимое. Двузначное число с 1 единицей, которое делится без остатка на двузначное число с 7 единицами. Это число 81, которое разделили на 27, получится 3.
Остаток после деления первого неполного делимого – 8.
5 + 8 = 13
Значит, смогли разделить не 14 десятков, а 13. Первое неполное неделимое – 143, а смогли разделить 135.
135 : 7 = 5
Оформляем задание в тетрадь.
Номер 5.
Многие крупные животные могут развивать большую скорость, но только на короткое время (на 3 – 5 мин). Ниже указаны именно такие скорости. Расположи всех этих животных в порядке уменьшения скорости их бега.
Прежде чем сравнить скорости животных и расположить их в порядке уменьшения скорости бега нужно привести скорости к одним единицам. Это будут км/ч.
1) Гепард: 30 м/с: 30м = 30 ∙ 3600 = 108000 м/ч = 108 км/ч
2) Антилопа: 25 м/с = 25 ∙ 3600 = 90000 м/ч = 90 км/ч
3) Лев: 80 км/ч
4) Страус: 500 м/мин = 500 ∙ 60 = 30000 м/ч = 30 км/ч
5) Зебра: 1 км/мин = 1 ∙ 60 = 60 км/ч
6) Жираф: 750 м/мин = 750 ∙ 60 = 45000 м/ч = 45 км/ч
Расположим животных, согласно уменьшению скорости их бега:
Номер 6.
Вырази скорости всех животных в одних и тех же единицах скорости. Выбери масштаб и построй диаграмму их скоростей.
Ответ:
Номер 7.
Составь задачи по чертежам и реши их.
1)
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 81, номер 7, условие 1, 2024 год.")
Через сколько времени расстояние между ними будет равно 700 км?
2)
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 81, номер 7, условие 2, 2024 год.")
На каком расстоянии друг от друга они будут через 3 ч?
Задача 1:
Два автомобиля выехали в противоположных направлениях из двух городов, расстояние между которыми равно 100 км. Первый автомобиль ехал со скоростью 60 км/ч, а второй – 90 км/ч. Через какое время расстояние между ними будет равно 700 км?
1) 700 − 100 = 600 (км) – должны проехать автомобили.
2) 60 + 90 = 150 (км/ч) – скорость удаления.
3) 600 : 150 = 4 (ч) – время через которое расстояние между автомобилями будет равняться 700 километрам.
Ответ: расстояние между автомобилями будет равняться 700 километрам составляет 4 ч.
Задача 2:
Два лыжника отправились на встречу друг другу из двух пунктов, расстояние между которыми равно 90км. Первый лыжник ехал со скоростью 12 км/ч, а второй – 15 км/ч. На каком расстоянии они будут друг от друга через 3 ч?
1) 15 + 12 = 27 (км/ч) – скорость сближения.
2) 27 ∙ 3 = 81 (км) – проедут лыжники.
3) 90 − 81 = 9 (км) – расстояние между лыжниками через 3 часа.
Ответ: расстояние между лыжниками через 3 часа составляет 9 км.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽
Напишите свой комментарий.