Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 80

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Странички для любознательных
Готовимся к олимпиаде
Номер 1.
Восстанови пропущенные цифры.


Повтори алгоритм письменного сложения, вычитания, умножения и деления.
Восстановим пропущенные записи методом подбора.
1. 9 + 1 = 10. А в единицах получилось 8. Значит, недостающая цифра – 8, так как 10 + 8 = 18. 1 дес. запомню и прибавлю к десяткам.
7 + 0 = 7, да ещё 1. 7 + 1 = 8. А в десятках получилось 6. Значит, недостающая цифра – 8, так как 8 + 8 = 16. 1 сот. запомню и прибавлю к сотням.
3 + 6 = 9, да ещё 1. 9 + 1 = 10. А в сотнях получилось 5. Значит, недостающая цифра – 5, так как 10 + 5 = 15. 1 ед. тыс. запомню и прибавлю к единицам тысяч.
3 + 4 + 5 = 12, да еще 1. 12 + 1 = 13. Пишу 3 под единицами тысяч, а 1 под десятками тысяч.
2. Из однозначного числа нельзя вычесть 9, чтобы получилось 5. Возьмём 1 дес. Значит, недостающая цифра – 4, так как 14 – 9 = 5.
Было 3 дес., 1 дес. взяли при вычитании единиц, осталось 2 дес. В десятках получилось 0, значит, недостающая цифра – 2, так как 2 – 2 = 0.
После вычитания 1 сот., в сотнях получилось 7, значит, недостающая цифра – 8, так как 8 – 1 = 7.
3. Чтобы при умножении на однозначное число получился 0, нужно умножать на 5.
8 ∙ 5 = 40. 4 дес. запомню и прибавлю к десяткам после умножения десятков.
4 ∙ 5 = 20, да ещё 4 дес., которые получились при умножении единиц.
20 + 4 = 24. Пишу 4 под десятками, а 2 сот. запомню и прибавлю к сотням.
После того, как к сотням прибавили 2 сот., которые получились при умножении десятков, в сотнях получилось 7. Значит, при умножении сотен получилось 7 – 2 = 5. 5 : 5 = 1. Значит, недостающая цифра в первом множителе – 1.
При делении однозначного числа на 7, получилось 1. Значит, первое неполное делимое – 7, так как 7 : 7 = 1. 4 меньше 7, значит в частном пишем 0.
Двузначное число с 4 десятками разделили на 7 и получилось 6. Это число 42. Значит, недостающая цифра – 2.
Оформим задание в тетрадь.

Номер 2.
В двух наборах 18 кубиков. Количество кубиков в одном наборе составляет половину кубиков в другом. Сколько кубиков в каждом наборе?
Ответ:
Первый набор = половина второго набора.
Второй набор = первый набор + первый набор.
А всего кубиков = первый набор + второй набор.
Подставим вместо второго набора сумму двух первых, ведь первый набор - половина второго.
18 кубиков = первый набор + первый набор + первый набор
Значит: 18 = первый набор ∙ 3
Первый набор = 6 кубиков.
Первый набор – половина второго, значит второй набор = 2 ∙ 6 = 12 кубиков.
Ответ: 6 кубиков всего в первой наборе и 12 кубиков всего во втором наборе.
Повтори, что такое отрезок и доли.
Оформляем условие в виде схематического чертежа.

Рассуждаем.
Первый набор = половина второго набора.
Второй набор = первый набор + первый набор.
А всего кубиков = первый набор + второй набор.
Продолжаем рассуждение.
Подставим вместо второго набора сумму двух первых, ведь первый набор – половина второго.
18 кубиков = первый набор + первый набор + первый набор.
Значит: 18 = первый набор ∙ 3.
Первый набор = 6 кубиков.
Первый набор – половина второго, значит второй набор = 2 ∙ 6 = 12 кубиков.
Записываем ответ.
Ответ: 6 кубиков и 12 кубиков.
Номер 3.
Лена в 3 раза моложе брата Саши, а вместе им 20 лет. Сколько лет Саше? Сколько лет Лене?
Ответ:
Возраст Саши = Лена ∙ 3
20 лет = возраст Саши + возраст Лены.
Подставим в выражение вместо возраста Саши – Лена ∙ 3
20 лет = Лена ∙ 3 + Лена
20 лет = Лена ∙ 4,значит возраст Лены – 5 лет.
Тогда возраст Саши – 15 лет, ведь он в три раза старше сестры.
Ответ: возраст Лены составляет 5 лет и возраст Саши составляет 15 лет.
Повтори, что такое доли, отрезок, а также единицу времени – год.
Оформляем условие в виде схематического чертежа.

Рассуждаем.
Возьмем один отрезок за возраст Лены, значит возраст Саши 3 таких отрезка, так как Лена в 3 раза моложе Саши.
Получается 4 одинаковых отрезка. Это 20 лет. Вычислим возраст Лены, что является одним отрезком.
1) 20 : 4 = 5 (л.) – возраст Лены
Продолжаем рассуждение.
Если 1 отрезок соответствует возрасту 5 лет, то возраст Саши – в 3 раза больше. Узнаем возраст Саши.
2) 5 ∙ 3 = 15 (л.)
Записываем ответ.
Ответ: Лене – 5 лет, а Саше – 15 лет.
Номер 4.
Спектакль начинается в 17 ч. В какое время Миша должен выйти из дома, если он хочет быть в театре за полчаса до начала спектакля, а на дорогу до дома до театра у него уходит 20 мин пешком от дома до метро, 15 мин поездом на метро и 10 мин пешком от метро до театра?
Ответ:
1) 17 ч − 30 мин = 16 ч 30 мин – время, когда Миша хочет быть в театре.
2) 20 + 15 + 10 = 45 мин – время на дорогу.
3) 16 ч 30 мин − 45 мин = 15 ч 45 мин – время выхода Миши из дома.
Ответ: Миша вышел из дома в 15 ч 45 мин.
Повтори единицы времени – час и минуту.
Оформляем условие в виде краткой записи.

Рассуждаем.
Вычислим, за сколько времени Мише нужно выходить из дома.
1) 20 + 15 + 10 + 30 = 75 (мин) = 1 ч 15 мин
Продолжаем рассуждение.
Узнаем, в какое время Миша должен выйти из дома.
2) 17 ч – 1 ч 15 мин = (17 ч – 1 ч) – 15 мин = 15 ч + (60 мин – 15 мин) = 15 ч 45 мин
Записываем ответ.
Ответ: Миша должен выйти в 15 ч 45 мин.
Номер 5.
Расставь знаки арифметических действий и, если нужно, скобки так, чтобы получились верные равенства.
Ответ:
(7 ∙ 7 − 7) : 7 = (49 − 7) : 7 = 42 : 7 = 6
7 + 7 + 7 : 7 = 14 + 1 = 15
7 : 7 + 7 : 7 = 1 + 1 = 2
7 ∙ 7 + 7 ∙ 7 = 49 + 49 = 98
(7 ∙ 7 + 7) : 7 = (49 + 7) : 7 = 56 : 7 = 8
(7 ∙ 7 − 7) ∙ 7 = (49 − 7) ∙ 7 = 42 ∙ 7 = 294
7 ∙ 7 − 7 : 7 = 49 − 1 = 48
7 ∙ 7 + 7 : 7 = 49 + 1 = 50
Повтори случаи табличного умножения и деления, а также порядок действий.
Выполняем вычисления.
(7 ∙ 7 − 7) : 7 = (49 − 7) : 7 = 42 : 7 = 6
7 + 7 + 7 : 7 = 14 + 1 = 15
7 : 7 + 7 : 7 = 1 + 1 = 2
7 ∙ 7 + 7 ∙ 7 = 49 + 49 = 98
(7 ∙ 7 + 7) : 7 = (49 + 7) : 7 = 56 : 7 = 8
(7 ∙ 7 − 7) ∙ 7 = (49 − 7) ∙ 7 = 42 ∙ 7 = 294
7 ∙ 7 − 7 : 7 = 49 − 1 = 48
7 ∙ 7 + 7 : 7 = 49 + 1 = 50
Оформляем задание в тетрадь.
(7 ∙ 7 – 7) : 7 = 6
7 + 7 + 7 : 7 = 15
7 : 7 + 7 : 7 = 2
7 ∙ 7 + 7 ∙ 7 = 98
(7 ∙ 7 + 7) : 7 = 8
(7 ∙ 7 – 7) ∙ 7 = 294
7 ∙ 7 – 7 : 7 = 48
7 ∙ 7 + 7 : 7 = 50
Номер 6.
Начерти отрезок длиной 12 см. Раздели его на две части так, чтобы одна часть была в 3 раза длиннее другой. Запиши длину каждой части.
Ответ:
Первая часть – х, а вторая в 3 раза длиннее её,
значит вторая часть = 3 ∙ х.
В сумме они должны быть 12 см.
Получается, что:
х + 3 ∙ х = 12
4 ∙ х = 12
х = 12 см
Длина первой части – 3 см, а второй 3 ∙ 3 = 9 см.
Ответ: длина первой части составляет 3 см и длина второй части составляет 9 см.
Повтори единицу длины – сантиметр, а также что такое отрезок и доли.
Оформляем условие в виде схематического чертежа.
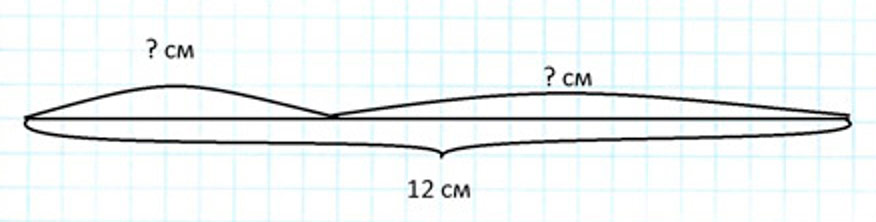
Составляем уравнение и решаем его.
Первая часть – х, а вторая в 3 раза длиннее её,
значит вторая часть = 3 ∙ х.
В сумме они должны быть 12 см.
Получается, что:
х + 3 ∙ х = 12
4 ∙ х = 12
х = 12 см
Длина первой части – 3 см, а второй 3 ∙ 3 = 9 см.
Записываем ответ.
Ответ: 3 см и 9 см.
Странички для любознательных
Номер 1.
Сокол медленно и плавно парит высоко в небе и, широко раскинув крылья, почти не шевелит ими, но, увидев на земле своим зорким взглядом маленькую зверушку, на которую он охотится, сокол складывает крылья и падает камнем вниз, развивая скорость до 360 км/ч. С какой высоты пикировал сокол, если у земли он оказался через 8 с?
Ответ:
Скорость – 360 км/ч
Время – 8 с
Расстояние – ? км
Переведем 360 км/ч в м/с. Для этого:
1) 360 км = 360 ∙ 1000 (потому что в 1 км – 1000 м) = 360000 метров.
2) 1 час = 60 ∙ 60 = 3600 секунд.
3) 360000 : 3600 = 100 (м/с) – скорость сокола.
4) 8 ∙ 100 = 800 (м) – высоты, с которой пикировал сокол.
Ответ: высота, с которой пикировал сокол составляет 800 м.
Номер 2.
Многие птицы осенью перелетают с севера на юг, в тёплые края. Учёные установили, что одна полярная крачка (чайка) пролетела расстояние 25600 км за 160 сут. Чирки за месяц (30 дней) пролетают 6000 км. Узнай, у кого средняя скорость полёта больше и на сколько километров с утки больше – у крачки или у чирка.
Ответ:
1) 25600 : 160 = 160 (км/сут.) – средняя скорость полёта крачки;
2) 6000 : 30 = 200 (км/сут.) – средняя скорость полёта чирки;
3) 200 – 160 = 40 (км/сут.) – на столько скорость чирки, больше скорости крачки.
Ответ: средняя скорость полёта чирки больше, чем у крачки, на 40 км/сут.
Номер 3.
Рассмотри и сравни данные, приведённые в следующей таблице, выразив скорость в одинаковых единицах.

1) 600 м/мин = 600 ∙ 60 = 36000 м/ч = 36 км/ч – скорость аиста. 2) 60 - 90 км/ч – скорость голубя. 3) воробей – 30 – 60 км/ч 4) 3 км/ч = 3 ∙ 60 = 180 км/ч – скорость стрижа. 5) 70 км/ч – примерная скорость колибри.

Номер 4.
Вырази скорость ветра в метрах в минуту; в метрах в час; в километрах в час.

Слабый ветер:
В метрах в минуту: 3 м/с = 3 ∙ 60 = 180 м/мин; 5 м/с = 5 ∙ 60 = 300 м/мин
В метрах в час: 3 м/с = 3 ∙ 60 ∙ 60 = 3 ∙ 3600 = 10800 м/ч; 5м/c = 5 ∙ 60 ∙ 60 = 5 ∙ 3600 = 18000 м/ч
В километрах в час: 3 м/с = (3 ∙ 60 ∙ 60) : 1000 = 11 км/ч: 5 м/с =(5 ∙ 60 ∙ 60) : 1000 = 18 км/ч
Сильный ветер:
В метрах в минуту: 15 м/с = 15 ∙ 60 = 900 м/мин; 18 м/с = 18 ∙ 60 = 1080 м/мин
В метрах в час: 15 м/с = 15 ∙ 60 ∙ 60 = 15 ∙ 3600 = 54000 м/ч; 18 м/с = 18 ∙ 60 ∙ 60 = 64800 м/ч
В километрах в час: 15 м/с = (15 ∙ 60 ∙ 60) : 1000 = 54 км/ч; 18 м/с = (18 ∙ 60 ∙ 60) : 1000 = 65 км/ч
Штормовой ветер:
В метрах в минуту: 20 м/с = 20 ∙ 60 = 1200 м/мин; 25 м/с = 25 ∙ 60 = 1500 м/мин
В метрах в час: 20 м/с = 20 ∙ 60 ∙ 60 = 72000 м/ч; 15 м/с = 15 ∙ 60 ∙ 60 = 90000 м/ч
В километрах в час: 20 м/с = (20 ∙ 60 ∙ 60) : 1000 = 72 км/ч; 25 м/с = (25 ∙ 60 ∙ 60) : 1000 = 90 км/ч
Ураганный ветер:
В метрах в минуту: 30 м/с = 30 ∙ 60 = 1800 м/мин
В метрах в час: 30 м/с = 30 ∙ 60 ∙ 60 = 108000 м/ч
В километрах в час: 30 м/с = (30 ∙ 60 ∙ 60) : 1000 = 108 км/ч
Ответ:
Скорость слабого ветра:
3 м/с − 5 м/с;
180 м/мин − 300 м/мин;
10800 м/ч − 18000 м/ч;
11 км/ч − 18 км/ч.
Скорость сильного ветра:
15 м/с − 18 м/с;
900 м/мин − 1080 м/мин;
54000 м/ч − 64800 м/ч;
54 км/ч − 65 км/ч.
Скорость штормового ветра:
20 м/с − 25 м/с;
1200 м/мин − 1500 м/мин;
72000 м/ч − 90000 м/ч;
72 км/ч − 90 км/ч.
Скорость ураганного ветра:
30 м/с;
1800 м/мин;
108000 м/ч;
108 км/ч.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.