Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 79
- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Номер 5.
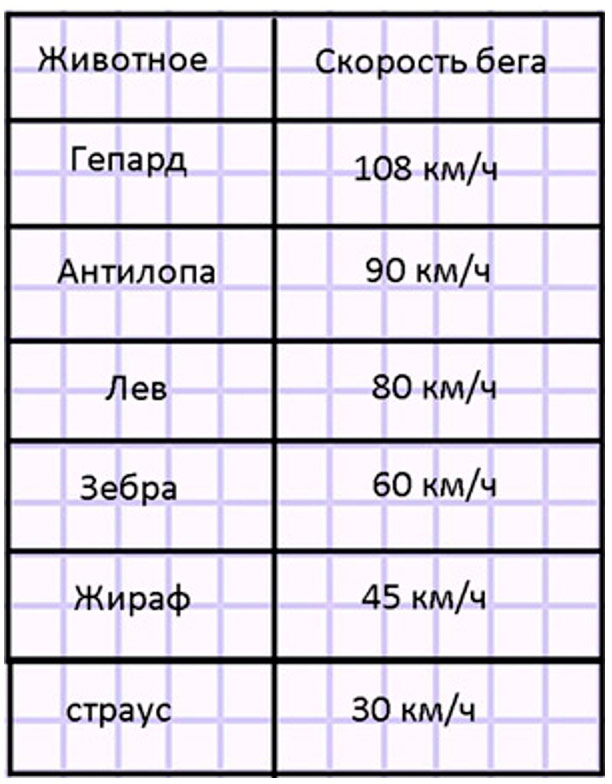
Многие крупные животные могут развивать большую скорость, но только на короткое время (на 3 – 5 мин). Ниже указаны именно такие скорости. Расположи всех этих животных в порядке уменьшения скорости их бега.
Прежде чем сравнить скорости животных и расположить их в порядке уменьшения скорости бега нужно привести скорости к одним единицам. Это будут км/ч.
1) Гепард: 30 м/с: 30м = 30 ∙ 3600 = 108000 м/ч = 108 км/ч
2) Антилопа: 25 м/с = 25 ∙ 3600 = 90000 м/ч = 90 км/ч
3) Лев: 80 км/ч
4) Страус: 500 м/мин = 500 ∙ 60 = 30000 м/ч = 30 км/ч
5) Зебра: 1 км/мин = 1 ∙ 60 = 60 км/ч
6) Жираф: 750 м/мин = 750 ∙ 60 = 45000 м/ч = 45 км/ч
Расположим животных, согласно уменьшению скорости их бега:
Повтори взаимосвязь между скоростью, временем и расстоянием.
Приведем скорости всех животных к одним единицам.
Прежде чем сравнить скорости животных и расположить их в порядке уменьшения скорости бега нужно привести скорости к одним единицам. Это будут км/ч.
1) Гепард: 30 м/с: 30м = 30 ∙ 3600 = 108000 м/ч = 108 км/ч
2) Антилопа: 25 м/с = 25 ∙ 3600 = 90000 м/ч = 90 км/ч
3) Лев: 80 км/ч
4) Страус: 500 м/мин = 500 ∙ 60 = 30000 м/ч = 30 км/ч
5) Зебра: 1 км/мин = 1 ∙ 60 = 60 км/ч
6) Жираф: 750 м/мин = 750 ∙ 60 = 45000 м/ч = 45 км/ч
Расположим всех животных в порядке уменьшения их скорости.
Расположим животных, согласно уменьшению скорости их бега:
Номер 6.
Вырази скорости всех животных в одних и тех же единицах скорости. Выбери масштаб и построй диаграмму их скоростей.
Ответ:
Повтори взаимосвязь между скоростью, временем и расстоянием.
Построим диаграмму по имеющимся данным.
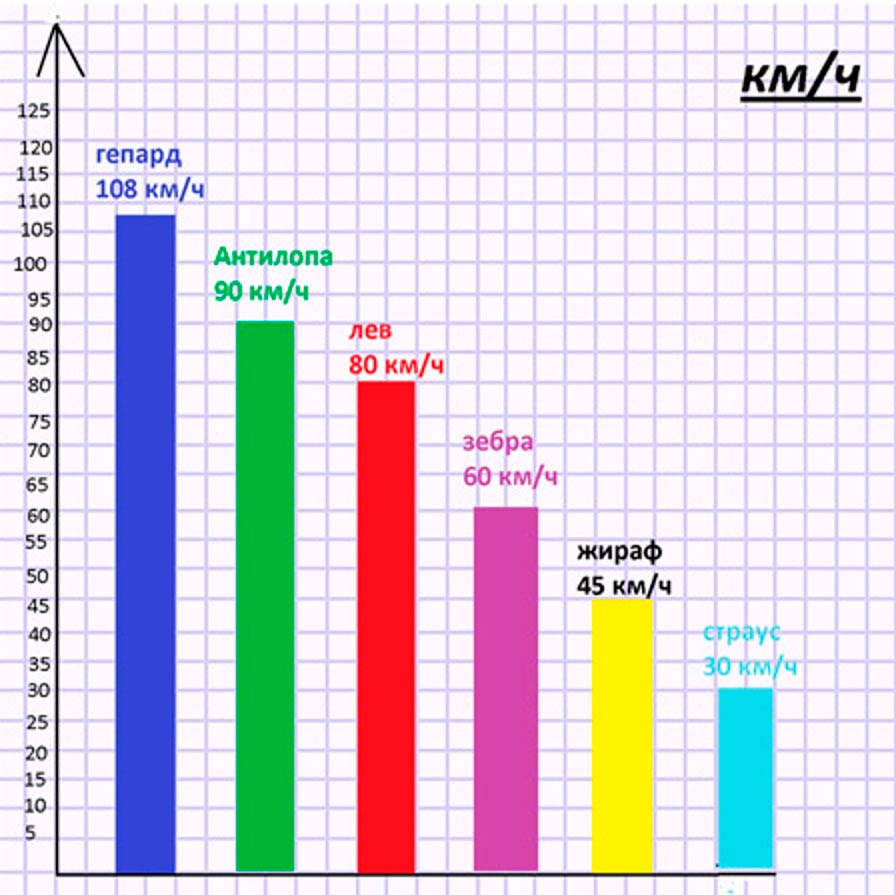
Оформим задание в тетрадь.
Номер 7.
Составь задачи по чертежам и реши их.
1)
.jpg "Изображение математика 4 класс Моро, Бантова - 2 часть страница 79, номер 7, условие 1")
Через сколько времени расстояние между ними будет равно 700 км?
2)
.jpg "Изображение математика 4 класс Моро, Бантова - 2 часть страница 79, номер 7, условие 2")
На каком расстоянии друг от друга они будут через 3 ч?
Задача 1:
Два автомобиля выехали в противоположных направлениях из двух городов, расстояние между которыми равно 100 км. Первый автомобиль ехал со скоростью 60 км/ч, а второй – 90 км/ч. Через какое время расстояние между ними будет равно 700 км?
1) 700 − 100 = 600 (км) – должны проехать автомобили.
2) 60 + 90 = 150 (км/ч) – скорость удаления.
3) 600 : 150 = 4 (ч) – время через которое расстояние между автомобилями будет равняться 700 километрам.
Ответ: 4 ч.
Задача 2:
Два лыжника отправились на встречу друг другу из двух пунктов, расстояние между которыми равно 90 км. Первый лыжник ехал со скоростью 12 км/ч, а второй – 15 км/ч. На каком расстоянии они будут друг от друга через 3 ч?
1) 15 + 12 = 27 (км/ч) – скорость сближения.
2) 27 ∙ 3 = 81 (км) – проедут лыжники.
3) 90 − 81 = 9 (км) – расстояние между лыжниками через 3 часа.
Ответ: расстояние между лыжниками через 3 часа составит 9 км.
Повтори взаимосвязь между скоростью, временем и расстоянием.
Шаг 1.
Составляем задачу по первому чертежу.
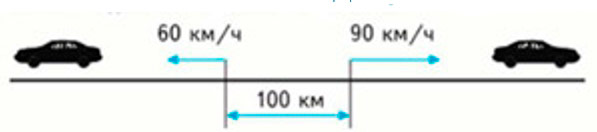
Два автомобиля выехали в противоположных направлениях из двух городов, расстояние между которыми равно 100 км. Первый автомобиль ехал со скоростью 60 км/ч, а второй – 90 км/ч. Через какое время расстояние между ними будет равно 700 км?
Рассуждаем.
Узнаем, сколько километров автомобили будут в пути.
1) 700 − 100 = 600 (км) – должны проехать автомобили.
Продолжаем рассуждение.
Найдем скорость удаления автомобилей.
2) 60 + 90 = 150 (км/ч) – скорость удаления.
Продолжаем рассуждение.
Найдем время, через которое расстояние между автомобилями будет равняться 700 километрам.
3) 600 : 150 = 4 (ч)
Записываем ответ.
Ответ: 4 часа – время через которое расстояние между автомобилями будет равняться 700 километрам.
Шаг 1.
Составляем задачу по второму чертежу.
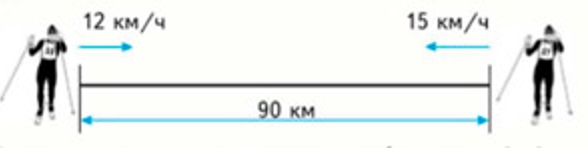
Два лыжника отправились на встречу друг другу из двух пунктов, расстояние между которыми равно 90км. Первый лыжник ехал со скоростью 12 км/ч, а второй – 15 км/ч. На каком расстоянии они будут друг от друга через 3 ч?
Рассуждаем.
Найдем скорость сближения лыжников.
1) 15 + 12 = 27 (км/ч) – скорость сближения.
Продолжаем рассуждение.
Узнаем, сколько км займет путь лыжников.
2) 27 ∙ 3 = 81 (км) – проедут лыжники.
Продолжаем рассуждение.
Узнаем, каким будет расстояние между лыжниками через 3 часа.
3) 90 − 81 = 9 (км)
Записываем ответ.
Ответ: 9 км расстояние между лыжниками через 3 часа.
Задание вверху страницы
Найди ошибки и запиши правильное решение.
Ответ:
Повтори алгоритм письменного деления на двузначные и трёхзначные числа.
Рассуждаем.
В данном примере пропустили второе неполное делимое — 28.
Выполним правильные вычисления.
21888 : 36 = 608
Разделю 21888 на 36. Выделю первое неполное делимое — 218.
Разделю 218 на 36, получу 6 — это пробная цифра.
Проверяю, подходит ли цифра 6.
Умножу 36 на 6, получу 216.
218 – 216 = 2. Добавляю 8 дес.
Нахожу вторую цифру частного: 28 : 36.
28 < 36, пишу в частном 0. Добавляю 8 ед.
Нахожу третью цифру частного:
288 : 36, получу 8.
Умножу 36 на 8, получу 288.
288 – 288 = 0.
Частное — 608.
Продолжаем рассуждение.
В данном примере пропустили третье неполное делимое — 0.
Выполним правильные вычисления.
322920 : 46 = 7020
Разделю 322920 на 46. Выделю первое неполное делимое — 322.
Разделю 322 на 46, получу 7 — это пробная цифра.
Проверяю, подходит ли цифра 7.
Умножу 46 на 7, получу 322.
322 – 322 = 0. Добавляю 9 сот.
Нахожу вторую цифру частного: 9 : 46.
9 < 46, пишу в частном 0. Добавляю 2 дес.
Нахожу третью цифру частного:
92 : 46, получу 2.
Умножу 46 на 2, получу 92.
92 – 92 = 0. Добавляю 0 ед.
Нахожу четвёртую цифру частного:
0 : 46, получу 0.
Частное — 7020.
Продолжаем рассуждение.
В данном примере неправильно подобрали первую цифру частного, так как остаток получился больше делителя.
Выполним правильные вычисления.
11352 : 132 = 86
Разделю 11352 на 132. Выделю первое неполное делимое — 1135.
Разделю 1135 на 132, получу 8 — это пробная цифра.
Проверяю, подходит ли цифра 8.
Умножу 132 на 8, получу 1056.
1135 – 1056 = 79. Добавляю 2 ед.
Нахожу вторую цифру частного:
792 : 132, получу 6.
Умножу 132 на 6, получу 792.
792 – 792 = 0.
Частное — 86.
Оформляем задание в тетрадь.
Номер 331.
Ответ:
Повтори алгоритм письменного умножения и деления на двузначные и трёхзначные числа.
Выполняем вычисления.
518 ∙ 204 = 105672
Умножу первый множитель на число единиц: 518 ∙ 4 = 2072.
Получу первое неполное произведение: 2072.
В десятках второго множителя — ноль, поэтому пропускаем этап умножения на десятки.
Умножу первый множитель на число сотен: 518 ∙ 2 = 1036.
Получу второе неполное произведение: 1036 сот.
Начну подписывать второе неполное произведение под сотнями.
Сложу неполные произведения.
Читаю ответ: 105672. Это произведение чисел 518 и 204.
766 ∙ 530 = 405980
Ноль смещаем вправо и не учитываем его в умножении.
Умножу первый множитель на число единиц: 766 ∙ 3 = 2298.
Получу первое неполное произведение: 2298.
Умножу первый множитель на число десятков: 766 ∙ 5 = 3830.
Получу второе неполное произведение: 3830 дес.
Начну подписывать второе неполное произведение под десятками.
Сложу неполные произведения. Допишу к ответу ноль из второго множителя.
Читаю ответ: 405980. Это произведение чисел 766 и 530.
283410 : 603 = 470
Выделю первое неполное делимое — 834.
Чтобы легче было найти цифру частного, разделим 2800 на 600.
Для этого разделим 28 на 6, в частном получим 4.
Это пробная цифра, её нужно проверить.
Умножу 603 на 4, получится 2412.
2834 – 2412 = 422. Добавим 1 дес.
Нахожу вторую цифру частного: 4221 : 603, получу 7.
Умножу 603 на 7, получу 4221.
4221 – 4221 = 0.
Нахожу третью цифру частного:
0 : 603 = 0.
Частное 470.
166520 : 724 = 230
Выделю первое неполное делимое — 1665.
Чтобы легче было найти цифру частного, разделим 1600 на 700.
Для этого разделим 16 на 7, в частном получим 2.
Это пробная цифра, её нужно проверить.
Умножу 724 на 2, получится 1448.
1665 – 1448 = 217. Добавим 2 дес.
Нахожу вторую цифру частного: 2172 : 724, получу 3.
Умножу 724 на 3, получу 2172.
2172 – 2172 = 0.
Нахожу третью цифру частного: 0 : 724 = 0.
Частное 230.
435 ∙ 87 = 37845
Умножу первый множитель на число единиц: 35 ∙ 7 = 3045.
Получу первое неполное произведение: 3045.
Умножу первый множитель на число десятков: 435 ∙ 8 = 3480.
Получу второе неполное произведение: 3480 дес.
Начну подписывать второе неполное произведение под десятками.
Сложу неполные произведения.
Читаю ответ: 37845. Это произведение чисел 435 и 87.
608 ∙ 95 = 57760
Умножу первый множитель на число единиц: 608 ∙ 5 = 3040.
Получу первое неполное произведение: 3040.
Умножу первый множитель на число десятков: 608 ∙ 9 = 5472.
Получу второе неполное произведение: 5472 дес.
Начну подписывать второе неполное произведение под десятками.
Сложу неполные произведения.
Читаю ответ: 57760. Это произведение чисел 608 и 95.
5476 : 37 = 148
Выделю первое неполное делимое — 54.
Чтобы легче было найти цифру частного, разделим 50 на 30.
Для этого разделим 5 на 3, в частном получим 1.
Это пробная цифра, её нужно проверить.
Умножу 37 на 1, получится 37.
54 – 37 = 17. Добавим 7 дес.
Нахожу вторую цифру частного:
177 : 37, получу 4.
Умножу 37 на 4, получу 148.
177 – 148 = 29. Добавим 6 ед.
Нахожу третью цифру частного: 296 : 37 = 8.
Умножу 37 на 8, получу 296.
296 – 296 = 0.
Частное 148.
12098 : 46 = 263
Выделю первое неполное делимое — 120
Чтобы легче было найти цифру частного, разделим 120 на 40.
Для этого разделим 12 на 4, в частном получим 3.
Это пробная цифра, её нужно проверить.
Умножу 46 на 3, получится 138. Это больше, чем 120, значит, в частном должно быть меньше, чем 3. Пробую, подходит ли цифра 2.
Умножу 46 на 2, получится 92.
120 – 92 = 28. Добавим 9 дес.
Нахожу вторую цифру частного: 289 : 46, получу 6.
Умножу 46 на 6, получу 276.
289 – 276 = 13. Добавим 8 ед.
Нахожу третью цифру частного: 138 : 46 = 3.
Умножу 46 на 3, получу 138.
138 – 138 = 0.
Частное 263.
Оформляем задание в тетрадь.
Номер 332.
1) Вычисли произведение, если первый множитель 76 и он меньше второго множителя на 28.
2) Вычисли частное, если делимое 1792 и оно больше делителя на 1736.
Повтори, как называются числа при умножении и делении, а также алгоритм письменного вычитания, умножения и деления многозначных чисел.
Выполняем вычисления.
Первый множитель — 76, который меньше второго множителя на 28.
Найдём второй множитель:
76 + 28 = 104 — второй множитель
Найдём произведение:
76 ∙ 104 = 7904
Делимое — 1792, который больше делителя на 1736.
Найдём делитель:
1792 – 1736 = 56 — делитель
Найдём частное:
1792 : 56 = 32
Оформляем задание в тетрадь.
Номер 333.
Библиотеке нужно переплести 4500 книг. Одна мастерская может переплести эти книги за 30 дней, а другая – за 45. За сколько дней могут выполнить заказ обе эти мастерские, работая одновременно?
Ответ:
Первая мастерская – 4500 книг за 30 дн.
Вторая мастерская – 4500 книг за 45 дн.
Совместная работа – 4500 книг за ? дн.
1) 4500 : 30 = 150 (к.) – переплетает в день первая мастерская.
2) 4500 : 45 = 100 (к.) – переплетает в день вторая мастерская.
3) 150 + 100 = 250 (к.) – переплетут в день обе мастерские при совместной работе.
4) 4500 : 250 = 18 (дн.) – понадобятся, чтобы переплести 4500 книг при совместной работе.
Ответ: 18 дней всего понадобятся, чтобы переплести книги.
Повтори алгоритм письменного деления на двузначные и трёхзначные числа.
Оформляем условие в виде краткой записи.
Всего — 4500 книг
Ⅰ мастерская — за 30 дней
Ⅱ мастерская — за 45 дней
Вместе — за ? дней
Рассуждаем.
Узнаем, сколько книг переплетает в день первая мастерская. Для этого разделим количество книг на количество дней.
4500 : 30 = 150 (к.) — переплетает в день первая мастерская.
Продолжаем рассуждение.
Узнаем, сколько книг переплетает в день вторая мастерская. Для этого разделим количество книг на количество дней.
4500 : 45 = 100 (к.) — переплетает в день вторая мастерская.
Продолжаем рассуждение.
Узнаем, сколько книг переплетут в день обе мастерские, работая одновременно.
150 + 100 = 250 (к.) — переплетут в день обе мастерские, работая одновременно.
Продолжаем рассуждение.
Узнаем, за сколько дней могут выполнить заказ обе мастерские, работая одновременно.
4500 : 250 = 18 (дн.) — нужно, чтобы выполнить заказ.
Записываем ответ.
Ответ: за 18 дней могут выполнить заказ обе мастерские, работая одновременно.
Номер 334.
С книжного склада отправили в школы города 28800 учебников. В первую школу отправили четвёртую часть этих учебников, во вторую – 6300 учебников, а остальные учебники были отправлены в 3 школы, поровну в каждую. Сколько учебников получила каждая из этих трёх школ?
Ответ:
1) 28800 : 4 = 7200 (уч.) – отправили в первую школу.
2) 7200 + 6300 = 13500 (уч.) – отправили в первую и вторую школу вместе.
3) 28800 − 13500 = 15300 (уч.) – отправили в остальные три школы.
4) 15300 : 3 = 5100 (уч.) – получила каждая из трех школ.
Ответ: 5100 учебников всего получила каждая из трёх школ.
Повтори алгоритм письменного сложения, вычитания и деления многозначных чисел, а также что такое доли.
Оформляем условие в виде краткой записи.
Рассуждаем.
Узнаем, какое количество учебников отправили в первую школу. Для этого разделим общее количество учебников на четыре части и возьмём одну из них.
28800 : 4 = 7200 (уч.) — отправили в первую школу.
Продолжаем рассуждение.
Узнаем, какое количество учебников отправили в первую и вторую школы вместе.
7200 + 6300 = 13500 (уч.) — отправили в первую и вторую школу вместе.
Продолжаем рассуждение.
Узнаем, какое количество учебников отправили в остальные три школы.
28800 − 13500 = 15300 (уч.) — отправили в остальные три школы.
Продолжаем рассуждение.
Узнаем, какое количество учебников получила каждая из этих трех школ.
15300 : 3 = 5100 (уч.)
Записываем ответ.
Ответ: 5100 учебников получила каждая из трех школ.
Номер 335.
У продавца было 25 ящиков с абрикосами, по 3 кг в каждом. Когда несколько ящиков с абрикосами было продано, у него осталось 15 кг абрикосов. сколько ящиков с абрикосами он продал? Сколькими способами можно решить задачу? Запиши все возможные решения.
Ответ:Было – 25 ящ. по 3 кг Продано – ? ящ. Осталось – 15 кг
1) 25 ∙ 3 = 75 (кг) – абрикосов было всего. 2) 75 − 15 = 60 (кг) – абрикосов было продано. 3) 60 : 3 = 20 (ящ.) – с абрикосами продал.
1) 15 : 3 = 5 (ящ.) – осталось. 2) 25 − 5 = 20 (ящ.) – было продано.
Ответ: 20 ящиков с абрикосами всего было продано.
Повтори случаи вне табличного умножения и деления, а также способы оформления краткой записи к задаче.
Шаг 1.
Оформляем условие в виде краткой записи.
Было — 25 ящ. по 3 кг
Продано — ? ящ.
Осталось — 15 кг
Рассуждаем.
Узнаем, сколько килограммов абрикосов было всего у продавца. Для этого количество ящиков умножим на количество килограммов абрикосов в каждом ящике.
25 ∙ 3 = 75 (кг) — абрикосов было всего.
Продолжаем рассуждение.
Узнаем, сколько килограммов абрикосов было продано. Для этого из общего количества килограммов абрикосов вычтем сколько осталось.
75 − 15 = 60 (кг) — абрикосов было продано.
Продолжаем рассуждение.
Узнаем, сколько ящиков с абрикосами было продано. Для этого количество проданных килограммов абрикосов разделим на количество килограммов абрикосов в каждом ящике.
60 : 3 = 20 (ящ.) — было продано.
Записываем ответ.
Ответ: 20 ящиков с абрикосами продал продавец.
Шаг 1.
Оформляем условие в виде краткой записи.
Было — 25 ящ. по 3 кг
Продано — ? ящ.
Осталось — 15 кг
Рассуждаем.
Узнаем, сколько ящиков с абрикосами осталось. Для этого количество оставшихся килограммов абрикосов разделим на количество килограммов абрикосов в каждом ящике.
15 : 3 = 5 (ящ.) — осталось.
Продолжаем рассуждение.
Узнаем, сколько ящиков с абрикосами было продано.
25 − 5 = 20 (ящ.) — было продано.
Записываем ответ.
Ответ: 20 ящиков с абрикосами было продано.
Номер 336.
Запиши уравнения и реши их.
1) Если неизвестное число умножить на 35, то получится 1505.
2) Если вычесть из 3010 неизвестное число, то получится 973.
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 79, номер 336, пример 1, 2024 год.")
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 79, номер 336, пример 2, 2024 год.")
Повтори, как решать уравнения.
Выполняем вычисления.
х ∙ 35 = 1505
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
х = 1505 : 35
х = 43
3010 – х = 973
Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.
х = 3010 – 973
х = 2037
Оформляем задание в тетрадь.
Номер 337.
Выпиши названия прямых, острых и тупых углов ломаной.
Прямые углы: ОМЕ. Острые углы: АВС, ВСD, CDK, DKE. Тупые углы: КЕМ.
Повтори виды углов и что такое ломаная.
Рассмотрим ломаную.
Назовем углы.
Прямые углы: ЕМО.
Острые углы: АВС, ВСD, CDK, DKE.
Тупые углы: КЕМ.
Задание внизу страницы
Найди длину ломаной ABCDKEMO в миллиметрах.
Длина ломаной: 27 ∙ 3 + 32 ∙ 2 + 20 + 31 = 196 мм
Повтори единицу длины — миллиметр, а также что такое ломаная.
Рассуждаем.
Чтобы найти длину ломаной ABCDKEMO, нужно измерить длину каждого отрезка ломаной, а затем сложить их.
AB = BC = CD = 27 мм
DK = 20 мм
KE = MO = 32 мм
EM = 31 мм
Найдём длину ломаной ABCDKEMO:
27 ∙ 3 + 20 + 32 ∙ 2 + 31 = 81 + 51 + 64 = 132 + 64 = 196 (мм) — длина ломаной.
Записываем ответ.
Ответ: длина ломаной 196 мм.
Задание на полях страницы
Продолжи.
(10 − 1) : 9 = 9 : 9 = 1 (100 − 1) : 9 = 99 : 9 = 11 (1000 − 1) : 9 = 999 : 9 = 111 (10000 − 1) : 9 = 9999 : 9 = 1111
Повтори случаи внетабличного деления.
Рассмотрим.
(10 − 1) : 9 = ☐
(100 − 1) : 9 = ☐
(1000 − 1) : 9 = ☐
Рассуждаем.
Чтобы продолжить последовательность примеров, решим имеющиеся примеры.
(10 − 1) : 9 = 9 : 9 = 1
(100 − 1) : 9 = 99 : 9 = 11
(1000 − 1) : 9 = 999 : 9 = 111
Продолжаем рассуждение.
К уменьшаемому в скобках в каждом последующем примере дописывают ноль, в результате к частному дописывается единица.
Запишем и решим следующий пример.
(10000 − 1) : 9 = 9999 : 9 = 1111
Оформляем задание в тетрадь.
(10 − 1) : 9 = 1
(100 − 1) : 9 = 11
(1000 − 1) : 9 = 111
(10000 − 1) : 9 = 1111
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽
Напишите свой комментарий.