Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 76

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 308.
Проверь, правильно ли выполнено деление с остатком:
Ответ:
Повтори деление с остатком, а также алгоритм письменного деления многозначных чисел.
Проверяем, правильно ли выполнено деление с остатком.
Чтобы проверить деление с остатком, нужно частное умножить на делитель и к полученному результату прибавить остаток, в результате вычислений должно получится делимое.
Правильно выполненное деление:
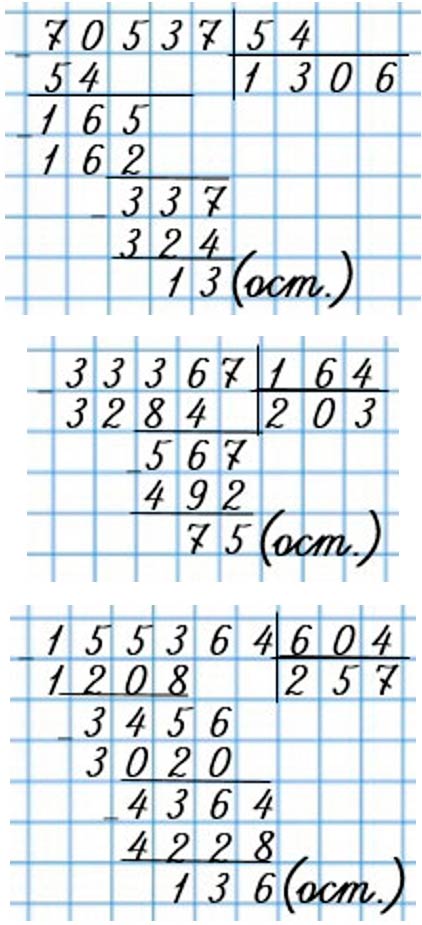
Оформляем задание в тетрадь.

Номер 309.
Найди делимое, если известно, что:
1) делитель 34, частное 8050, остаток 12;
2) делитель 46, частное 3080, остаток 35. Проверь, выполнив деление.

Проверь, как называются числа при делении.
Выполняем вычисления с проверкой.

Оформляем задание в тетрадь.
1) 8 050 ∙ 34 + 12 = 273 712
2) 3 080 ∙ 46 + 35 = 141 715
Номер 310.
Два опытных участка имеют одинаковую площадь. Ширина первого участка 60 м, а ширина второго 80 м. Найди длину первого участка, если известно, что длина второго участка 150 м. Сделай по задаче чертёж и реши задачу.
Ответ:
1) 150 ∙ 80 = 12000 (м²) – площадь второго участка.
2) 12000 : 60 = 200 (м) – длина первого участка.
Ответ: длина первого участка составляет 200 метров.
Повтори единицу длины – метр, единицы площади, а также как найти площадь прямоугольника.
Оформляем условие в виде схематического чертежам.
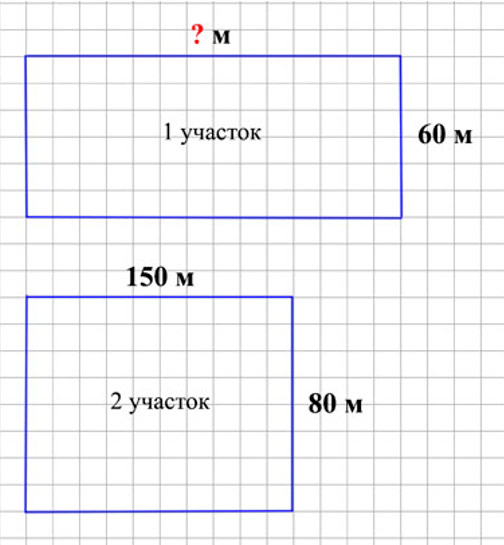
Рассуждаем.
Найдем площадь второго участка, для этого длину умножим на ширину.
1) 150 ∙ 80 = 12000 (м²) – площадь второго участка.
Продолжаем рассуждение.
Найдем длину первого участка.
2) 12000 : 60 = 200 (м)
Записываем ответ.
Ответ: 200 метров длина первого участка.
Номер 311.
Одна бригада рабочих может заасфальтировать 15 км шоссейной дороги за 30 дней, а другая – за 60 дней. За сколько дней могут заасфальтировать эту дорогу обе бригады, работая вместе?
Ответ:
Первая бригада - 15 км за 30 дней
Вторая бригада - 15 км за 60 дней
Совместная работа - 15 км за ? дней
15 км = 15000 м
1) 15000 : 30 = 500 (м) – дороги в день заасфальтирует первая бригада.
2) 15000 : 60 = 250 (м) – дороги в день заасфальтирует вторая бригада.
3) 500 + 250 = 750 (м) – дороги в день заасфальтируют обе бригады при совместной работе.
4) 15000 : 750 = 20 (дн.) – понадобится двум бригадам, чтобы заасфальтировать всю дорогу при совместной работе.
Ответ: 20 дней всего понадобится двум бригадам, чтобы заасфальтировать всю дорогу при совместной работе.
Повтори единицы длины – метр и километр, а также алгоритм письменного деления.
Оформляем условие в виде таблицы.

Рассуждаем.
15 км = 15000 м
Узнаем, сколько дороги в день заасфальтирует первая бригада.
1) 15000 : 30 = 500 (м) – дороги в день заасфальтирует первая бригада.
Продолжаем рассуждение.
Узнаем, сколько дороги в день заасфальтирует вторая бригада.
2) 15000 : 60 = 250 (м) – дороги в день заасфальтирует вторая бригада.
Продолжаем рассуждение.
Узнаем, сколько дороги в день заасфальтируют обе бригады при совместной работе.
3) 500 + 250 = 750 (м) – дороги в день заасфальтируют обе бригады при совместной работе.
Продолжаем рассуждение.
Сколько дней понадобится двум бригадам, чтобы заасфальтировать всю дорогу при совместной работе.
4) 15000 : 750 = 20 (дн.)
Записываем ответ.
Ответ: 20 дней понадобится двум бригадам, чтобы заасфальтировать всю дорогу при совместной работе.
Номер 312.
Поезд отправился из Санкт-Петербурга в 23 ч 15 мин прибыл в Москву в 6 ч 25 мин следующего дня. По пути он сделал 2 остановки: на станции Бологое и в городе Твери, по 5 мин каждая. С какой скоростью двигался этот поезд, если он прошел 651 км?
Ответ:
Выехал - в 23 ч 15 мин вчерашнего дня
Прибыл - в 6 ч 25 мин сегодняшнего дня
Остановки - 2 раза по 5 мин
S - 651 км
V - ? км/ч
1) 24 ч − 23 ч 15 мин = 45 (мин) – время движения первые сутки.
2) 6 ч 25 мин + 45 мин = 7 ч 10 мин – время движения с остановками.
3) 5 ∙ 2 = 10 (мин) – время остановок.
4) 7 ч 10 мин - 10 мин = 7 (ч) – время движения поезда.
5) 651 : 7 = 93 (км/ч) – скорость поезда.
Ответ: скорость поезда составляет 93 км/ч.
Повтори единицы времени – час и минуту, а также взаимосвязь между скоростью, временем и расстоянием.
Оформляем условие в виде краткой записи.
Выехал – в 23 ч 15 мин вчерашнего дня
Прибыл – в 6 ч 25 мин сегодняшнего дня
Остановки – 2 раза по 5 мин
S – 651 км
V – ? км/ч
Рассуждаем.
Узнаем, сколько займет время движения в первые сутки.
1) 24 ч − 23 ч 15 мин = 45 (мин) – время движения первые сутки.
Продолжаем рассуждение.
Узнаем, сколько займет время движения с остановками.
2) 6 ч 25 мин + 45 мин = 7 ч 10 мин – время движения с остановками.
Продолжаем рассуждение.
Узнаем, сколько займут времени остановки.
3) 5 ∙ 2 = 10 (мин) – время остановок.
Продолжаем рассуждение.
Узнаем, сколько займет время движения поезда.
4) 7 ч 10 мин – 10 мин = 7 (ч) – время движения поезда.
Продолжаем рассуждение.
Узнаем, какова скорость поезда.
5) 651 : 7 = 93 (км/ч)
Записываем ответ.
Ответ: 93 км/ч скорость поезда.
Номер 313.
Вычисли и выполни проверку.
Ответ:
Повтори алгоритм письменного сложения, вычитания, умножения и деления многозначных чисел.
Выполняем вычисления с пояснениями.
Пишу (единицы под единицами, десятки под десятками, сотни под сотнями, единицы тысяч под единицами тысяч, десятки тысяч под десятками тысяч): 85 493 + 7 309.
Складываю единицы: 3 + 9 = 12. 12 ед. – это 1 дес. и 2 ед.; 2 ед. пишу под единицами, а 1 дес. прибавлю к десяткам.
Складываю десятки: 9 + 0 = 9, да ещё 1.
9 + 1 = 10.
10 дес. – это 1 сот. и 0 дес.; 0 дес. пишу под десятками, а 1 сот. прибавлю к сотням.
Складываю сотни: 4 + 3 = 7, да ещё 1.
7 + 1 = 8.
Пишу под сотнями 8.
Складываю единицы тысяч: 5 + 7 = 12. 12 единиц тысяч – это 1 дес. тыс. и 2 ед. тыс.; 2 ед. тыс. пишу под единицами тысяч, а 1 дес. тыс. пишу под десятками тысяч, так как других десятков тысяч для сложения нет.
Читаю ответ: 92 802.
Чтобы проверить сложение, можно из суммы вычесть одно из слагаемых, при этом должно получится другое слагаемое.
Пишу (единицы под единицами, десятки под десятками, сотни под сотнями, единицы тысяч под единицами тысяч): 7 010 – 3 284.
Вычитаю единицы: из 0 ед. нельзя вычесть 4 ед. Беру 1 дес. из 1 дес. (Чтобы не забыть об этом, ставлю точку над цифрой 1.) 1 дес. и 0 ед. – это 10 ед. Из 10 вычесть 4, получится 6. Пишу под единицами 6.
Вычитаю десятки: был 1 дес., но 1 дес. взяли при вычитании единиц, осталось 0 дес. Из 0 дес. нельзя вычесть 8 дес. Взять 1 сот. из 0 нельзя, поэтому беру 1 ед. тыс. из 2 ед. тыс. (Чтобы не забыть об этом, ставлю точку над цифрой 7). 1 ед. тыс. – это 10 сот. Из 10 сот. беру 1 сот. (Чтобы не забыть об этом, ставлю точку над цифрой 0). 1 сот. и 0 дес. – это 10 дес. Из 10 вычесть 8, получится 2. Пишу под десятками 2.
Вычитаю сотни: было 10 сот., но 1 сот. взяли при вычитании десятков, осталось 9 сот. Из 9 вычесть 2, получится 7. Пишу под сотнями 7.
Вычитаю единицы тысяч: было 7 ед. тыс., но 1 ед. тыс. взяли при вычитании сотен, осталось 6 ед. тыс. Из 6 вычесть 3, получится 3. Пишу 3 под единицами тысяч.
Читаю ответ: 3 726.
Чтобы проверить вычитание, можно к разности прибавить вычитаемое и в результате вычислений должно получится уменьшаемое.
Пишу: 936 ∙ 23.
Умножу первый множитель на число единиц:
936 ∙ 3 = 2 808.
Получу первое неполное произведение:
2 808.
Умножу первый множитель на число десятков:
936 ∙ 2 = 1 872.
Получу второе неполное произведение:
1 872 дес.
Начну подписывать второе неполное произведение под десятками.
Сложу неполные произведения.
Читаю ответ: 21 528. Это произведение чисел 936 и 23.
Чтобы проверить умножение, можно произведение разделить на один из множителей и в результате вычислений должен получится другой множитель.
Пишу: 22 680 : 54.
Разделю 22 680 на 54. Выделю первое неполное делимое – 226. Разделю 22 на 5, получу 4 – это пробная цифра.
Проверяю, подходит ли цифра 4.
Умножу 54 на 4, получу 216.
226 – 216 = 10. Добавляю 8 дес.
Нахожу вторую цифру частного:
108 : 54, получу 2.
Умножу 54 на 2, получу 108.
108 – 108 = 0.
Нахожу третью цифру частного:
0 : 54, получу 0.
Частное – 420.
Пишу: 10 582 : 26.
Разделю 10 582 на 26. Выделю первое неполное делимое – 105. Разделю 10 на 2, получу 4 – это пробная цифра.
Проверяю, подходит ли цифра 4.
Умножу 26 на 4, получу 104.
105 – 104 = 1. Добавляю 8 дес.
Нахожу вторую цифру частного:
18 : 26. 18 меньше, чем 26, пишу в частном 0. Добавляю 2 ед.
Нахожу третью цифру частного:
182 : 26, получу 7.
Умножу 26 на 7, получу 182.
182 – 182 = 0.
Частное – 407.
Пишу: 11 359 : 37.
Разделю 11 359 на 37. Выделю первое неполное делимое – 113. Разделю 11 на 3, получу 3 – это пробная цифра.
Проверяю, подходит ли цифра 3.
Умножу 37 на 3, получу 111.
113 – 111 = 2. Добавляю 5 дес.
Нахожу вторую цифру частного:
25 : 37. 25 меньше, чем 37, пишу в частном 0. Добавляю 9 ед.
Нахожу третью цифру частного:
259 : 37, получу 7.
Умножу 37 на 7, получу 259.
259 – 259 = 0.
Частное – 307.
Чтобы проверить деление, можно частное умножить на делитель и в результате вычислений должно получится делимое.
Выполняем вычисления с проверкой и оформляем задание в тетрадь.

Номер 314.
Реши уравнения.
Ответ:
х − 640 = 921 : 3
х − 640 = 307
х = 307 + 640
х = 947
Проверка:
947 - 640 = 921 : 3
307 = 307
Ответ:х = 947
х : 9 = 2007 : 9
х : 9 = 223
х = 223 ∙ 9
х = 2007
Проверка:
2007 : 9 = 2007 : 9
223 = 223
Ответ:х = 2007
х ∙ 81 = 729 : 3
х ∙ 81 = 243
х = 243 : 81
х = 3
Проверка:
3 * 81 = 729 : 3
243 = 243
Ответ:х = 3
Повтори, как решать уравнения, а также алгоритм письменного умножения и деления трёхзначных чисел.
Выполняем вычисления с пояснениями.
В каждом из уравнений сначала выполняем вычисления в правой части.
921 : 3 = 307
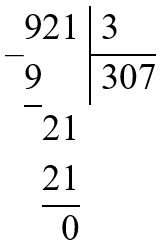
Чтобы найти уменьшаемое, нужно к вычитаемому прибавить разность:
640 + 307 = 947.
Проверка:
947 – 640 = 307
307 = 307
2 007 : 9 = 223
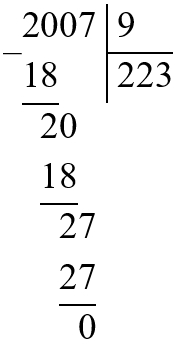
Чтобы найти делимое, нужно частное умножить на делитель:
223 ∙ 9 = 2 007.
Проверка:
2 007 : 9 = 2 007 : 9
223 = 223
729 : 3 = 243
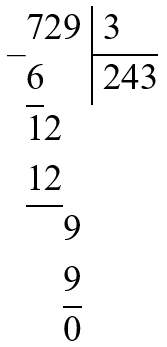
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель:
243 : 81 = 3.
Проверка:
3 ∙ 81 = 243
243 = 243
Оформляем задание в тетрадь.
х − 640 = 921 : 3
х − 640 = 307
х = 307 + 640
х = 947
Проверка:
947 − 640 = 921 : 3
307 = 307
х : 9 = 2007 : 9
х : 9 = 223
х = 223 ∙ 9
х = 2007
Проверка:
2007 : 9 = 2007 : 9
223 = 223
х ∙ 81 = 729 : 3
х ∙ 81 = 243
х = 243 : 81
х = 3
Проверка:
3 ∙ 81 = 729 : 3
243 = 243
Номер 315.
Как налить 5 л воды, используя десятилитровое ведро и трёхлитровую банку?
Ответ:1) Наполнить ведро, трижды налив туда воду из трехлитровой банки. 2) Наполнить еще одну трехлитровую банку и вылить в ведро 1 литр. 3) В ведре 10 литров, а в банке 2. 4) Выливаем воду из ведра и переливаем туда воду из банки. В банке 0 литров, а в ведре 2 литра. 5) Набираем еще 3 литра банкой и выливаем в ведро.
Повтори единицу объёма – литр.
Рассуждаем.
1) Наполнить ведро, трижды налив туда воду из трехлитровой банки.
2) Наполнить еще одну трехлитровую банку и вылить в ведро 1 литр.
3) В ведре 10 литров, а в банке 2.
4) Выливаем воду из ведра и переливаем туда воду из банки. В банке 0 литров, а в ведре 2 литра.
5) Набираем еще 3 литра банкой и выливаем в ведро.
Оформляем задание в тетрадь.
Задание внизу страницы
Периметр прямоугольника 11 дм 4 см, а длина одной его стороны 3 дм 2 см. Найди длину другой стороны этого прямоугольника.
Ответ:

1) 11 дм 4 см = 110 см + 4 см = 114 см
2) 114 : 2 = 57 (см) - полупериметр
3) 3 дм 2 см = 30 см + 2 см = 32 см
4) 57 - 32 = 25 (см) = 2 дм 5 см
Ответ: 2 дм 5 см. - длина другой стороны прямоугольника.
Повтори единицы длины – дециметр и сантиметр, а также как найти периметр прямоугольника.
Выполняем вычисления с пояснениями.
1 дм = 10 см
Периметр прямоугольника – это сумма длин всех его сторон. Мы знаем, что противоположные стороны прямоугольника равны. Поэтому можно сумму длины и ширины умножить на 2.
Удвоенная длина одной его стороны: (32 ∙ 2) см.
Удвоенная длина другой его стороны: (114 – 32 ∙ 2).
Найдём длину другой его стороны: (114 – 32 ∙ 2) : 2 = 50 : 2 = 25 (см) = 2 дм 5 см
Оформляем задание в тетрадь.
1) 11 дм 4 см : 2 = 5 дм 7 см – длина двух сторон прямоугольника.
2) 5 дм 7 см − 3 дм 2 см – длина другой стороны.
Ответ: 2 дм 5 см.
Задание на полях страницы
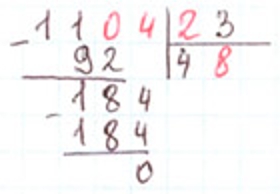
Ребус.

Ответ:

Повтори алгоритм письменного деления на двузначные числа.
Рассмотрим ребус.

Разгадаем ребус.
При умножении какого двузначного числа на 4 получается 92? Это число 23. Пишу 2 в делитель.
После того, как из первого неполного делимого вычли 92, получилось 18. 92 + 18 = 110. Пишу 0 в первое неполное делимое.
Так как во втором неполном делимом 4 единицы, значит последняя цифра в исходном числе тоже 4.
184 : 23 = 8. Пишу 8 в частном.
Выполняем проверку.
Номер 305.
Вычисли с объяснением.
Ответ:
Нужно разделить 30033 на 423.
Чтобы легче было найти цифру частного, разделим 3003 на 400.
Для этого разделим 30 на 4, в частном получим 7.
Это пробная цифра, её нужно проверить.
Умножим 423 на 7, получится 2961.
Вычтем 2961 из 3003, получим 42.
Добавим к нему оставшиеся 3 единицы – 423.
Находим вторую цифру частного: 423 : 423 = 1 (единица).
Частное – 71.
Нужно разделить 75435 на 321.
Чтобы легче было найти цифру частного, разделим 754 на 300.
Для этого разделим 7 на 3, в частном получим 2.
Это пробная цифра, её нужно проверить.
Умножим 321 на 2, получится 642.
Вычтем 642 из 754, получим 112.
Добавим к нему оставшиеся 3 десятка – 1123.
Находим вторую цифру частного: 1123 : 321 = 3.
Умножим 321 на 3, получится 963.
Вычтем 963 из 1123, получим 160.
Добавим к нему оставшиеся 5 единиц – 1605.
Находим третью цифру частного: 1605 : 321 = 5.
Частное – 235.
Номер 306.
Выполни деление и проверь вычисления.
Ответ:
Номер 307.
Ответ:
Номер 308.
Выполни чертёж и реши задачу.
Туристы прошли по реке на байдарках половину намеченного пути и ещё 9 км. Оставшийся путь они могут пройти на байдарках за 3 ч со скоростью 6 км/ч. Узнай весь путь, который должны были пройти туристы на байдарках.

1) 6 ∙ 3 = 18 (км) – осталось пройти туристам.
2) 18 + 9 = 27 (км) – половина намеченного пути.
3) 27 ∙ 2 = 54 (км) – длина всего маршрута, пройденного на байдарках.
Ответ: длина всего маршрута составляет 54 км.
Номер 309.
Составь задачу по выражению 81 : 3 − 57 : 3.
Ответ:
Два автомобиля ехали 3 ч. Первый автомобиль проехал – 81 км, а второй – 57 км. На сколько больше скорость первого автомобиля, чем второго?
1) 81 : 3 − 57 : 3 = 27 − 19 = 8 (км/ч) – на столько скорость первого автомобиля больше, чем скорость второго автомобиля.
Ответ: на 8 км/ч больше скорость первого автомобиля, чем второго автомобиля.
Номер 310.
В мастерской израсходовали 320 м шерстяной ткани и 340 м льняного полотна на пошив костюмов. Из шерстяной ткани сшили на 5 костюмов меньше, чем из льняного полотна. На каждый костюм расходовали одинаковое количество ткани. Сколько сшили костюмов из шерстяной ткани и сколько из льняного полотна?
Ответ:
1) 340 − 320 = 20 (м) – расход льняного полотна на 5 костюмов.
2) 20 : 5 = 4 (м) – расход льняного полотна на 1 костюм.
3) 320 : 4 = 80 (к.) – сшили из шерстяной ткани.
4) 340 : 4 = 85 (к.) – сшили из льняного полотна.
Ответ: 80 костюмов сшили всего из шерстной ткани и 85 костюмов всего сшили из льняного полотна.
Номер 311.
Составь по данным таблицы выражения и объясни, что они обозначают.

1) a : 6 (р.) − цена первого товара. 2) k : 4 (р.) − цена второго товара. 3) 20000 : b (р.) − цена третьего товара. 4) 40000 : c (р.) − цена четвертого товара. a + k + 20000 + 40000 = a + k + 60000 (р.) − стоимость всех покупок.
Номер 312.
Сравни выражения.
Ответ:
84 : (6 ∙ 2) и 84 : 6 ∙ 2
84 : 6 : 2 < 14 ∙ 2
84 : 12 < 14 ∙ 2
7 < 28
Значит, 84 : (6 ∙ 2) < 84 : 6 ∙ 2
45 ∙ 12 и 45 ∙ 2 ∙ 6
45 ∙ 12 = 45 ∙ 12
540 = 540
Значит, 45 ∙ 12 = 45 ∙ 2 ∙ 6
18 ∙ 15 и 18 ∙ 10 + 5
270 > 180 + 5
270 > 185
Значит, 18 ∙ 15 > 18 ∙ 10 + 5
28 ∙ 9 и 20 ∙ 9 + 8 ∙ 9
(20 + 8) ∙ 9 = 20 ∙ 8 + 8 ∙ 9
20 ∙ 9 + 8 ∙ 9 = 20 ∙ 9 + 8 ∙ 9
180 + 72 = 180 + 72
252 = 252
Значит, 28 ∙ 9 = 20 ∙ 9 + 8 ∙ 9
Номер 313.
Площадь классной доски прямоугольной формы 288 дм², а её длина 24 дм. Найди ширину доски. Составь обратные задачи и реши их.
Ответ:
S = a ∙ b
Длина - 24 дм
S - 288 дм²
Ширина - ? дм
288 : 24 = 12 (дм) – ширина доски.
Ответ: ширина доски составляет 12 дм.
Обратная задача 1:
Длина классной доски 24 дм, а ширина – 12 дм. Найди её площадь.
S = a ∙ b
Длина - 24 дм
Ширина - 12 дм
S - ? дм²
24 ∙ 12 = 288 (дм²) – площадь доски.
Ответ: площадь доски составляет 288 дм².
Обратная задача 2:
Площадь классной доски прямоугольной формы 288 дм², а её ширина 12 дм. Найди длину доски.
S = a ∙ b
Ширина - 12 дм
S - 288 дм²
Длина - ? дм
288 : 12 = 24 (дм) – длина доски.
Ответ: длина доски составляет 24 дм.
Задание внизу страницы
На склад привезли 4560 кг муки в мешках, по 80 кг в каждом, и 3840 кг крупы в мешках, по 60 кг в каждом. На сколько больше привезли мешков с крупой, чем с мукой?
Ответ:
1) 4560 : 80 = 57 (м.) – привезли на склад с мукой.
2) 3840 : 60 = 64 (м.) – привезли на склад с крупой.
3) 64 − 57 = 7 (м.) – на столько привезли на склад больше мешков с крупой, чем с мукой.
Ответ: на 7 штук больше привезли на склад мешков с крупой, чем с мукой.
Задание на полях страницы
Цепочка.

9000 → 300 → 3 → 2400 → 240 → 720

С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.