Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 74
- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
.jpg "Математика 4 класс Моро, Волкова - 2 часть страница 74")
Номер 290.
Вычисли с объяснением.
Ответ:
Нужно разделить 30033 на 423.
Чтобы легче было найти цифру частного, разделим 3003 на 400.
Для этого разделим 30 на 4, в частном получим 7.
Это пробная цифра, её нужно проверить.
Умножим 423 на 7, получится 2961.
Вычтем 2961 из 3003, получим 42.
Добавим к нему оставшиеся 3 единицы – 423.
Находим вторую цифру частного: 423 : 423 = 1 (единица).
Частное – 71.
Нужно разделить 75435 на 321.
Чтобы легче было найти цифру частного, разделим 754 на 300.
Для этого разделим 7 на 3, в частном получим 2.
Это пробная цифра, её нужно проверить.
Умножим 321 на 2, получится 642.
Вычтем 642 из 754, получим 112.
Добавим к нему оставшиеся 3 десятка – 1123.
Находим вторую цифру частного: 1123 : 321 = 3.
Умножим 321 на 3, получится 963.
Вычтем 963 из 1123, получим 160.
Добавим к нему оставшиеся 5 единиц – 1605.
Находим третью цифру частного: 1605 : 321 = 5.
Частное – 235.
Повтори алгоритм письменного деления на трёхзначные числа.
Выполняем вычисление с объяснением.
Нужно разделить 30033 на 423.
Чтобы легче было найти цифру частного, разделим 3003 на 400.
Для этого разделим 30 на 4, в частном получим 7.
Это пробная цифра, её нужно проверить.
Умножим 423 на 7, получится 2961.
Вычтем 2961 из 3003, получим 42.
Добавим к нему оставшиеся 3 единицы – 423.
Находим вторую цифру частного: 423 : 423 = 1 (единица).
Частное – 71.
Нужно разделить 75435 на 321.
Чтобы легче было найти цифру частного, разделим 754 на 300.
Для этого разделим 7 на 3, в частном получим 2.
Это пробная цифра, её нужно проверить.
Умножим 321 на 2, получится 642.
Вычтем 642 из 754, получим 112.
Добавим к нему оставшиеся 3 десятка – 1123.
Находим вторую цифру частного: 1123 : 321 = 3.
Умножим 321 на 3, получится 963.
Вычтем 963 из 1123, получим 160.
Добавим к нему оставшиеся 5 единиц – 1605.
Находим третью цифру частного: 1605 : 321 = 5.
Частное – 235.
Оформляем задание в тетрадь.
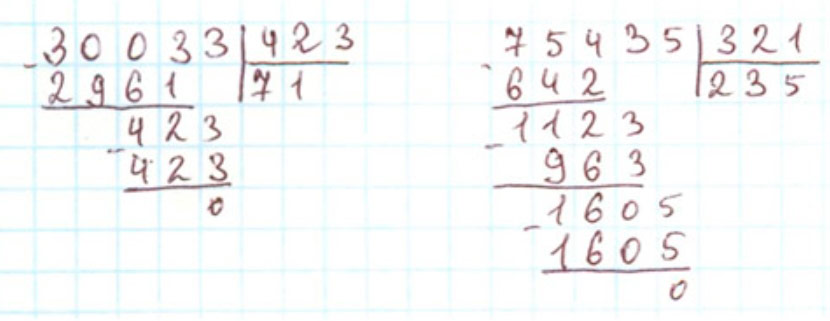
Номер 291.
Выполни деление и проверь вычисления.
Ответ:
Повтори алгоритм письменного деления на трёхзначные числа.
Выполняем вычисления с пояснениями.
Нужно разделить 22 134 : 714.
Выделю первое неполное делимое – 2 213.
Чтобы легче было найти цифру частного, разделим 2 213 на 700.
Для этого разделим 22 на 7, в частном получим 3.
Это пробная цифра, её нужно проверить.
Умножим 714 на 3, получится 2 142.
2 213 – 2 142 = 71. Добавим 4 ед.
Нахожу вторую цифру частного:
714 : 714 = 1.
Умножу 714 на 1, получу 714.
714 – 714 = 0.
Частное 31.
Нужно разделить 103 090 : 845.
Выделю первое неполное делимое – 1030.
Чтобы легче было найти цифру частного, разделим 1 030 на 800.
Для этого разделим 10 на 8, в частном получим 1.
Это пробная цифра, её нужно проверить.
Умножим 845 на 1, получится 845.
1 030 – 845 = 185. Добавим 9 дес.
Нахожу вторую цифру частного:
1 859 : 845, получу 2.
Умножу 845 на 2, получу 1 690.
1 859 – 1 690 = 169. Добавим 0 ед.
Нахожу третью цифру частного:
1 690 : 845 = 2.
Умножу 845 на 2, получу 1 690.
1 690 – 1 690 = 0.
Частное 122.
Нужно разделить 20 864 : 326.
Выделю первое неполное делимое – 2 086.
Чтобы легче было найти цифру частного, разделим 2 086 на 300.
Для этого разделим 20 на 3, в частном получим 6.
Это пробная цифра, её нужно проверить.
Умножим 326 на 6, получится 1 956.
2 086 – 1 956 = 130. Добавим 4 ед.
Нахожу вторую цифру частного:
1 304 : 326 = 4.
Умножу 326 на 4, получу 1 304.
1 404 – 1 304 = 0.
Частное 64.
Оформляем задание в тетрадь.
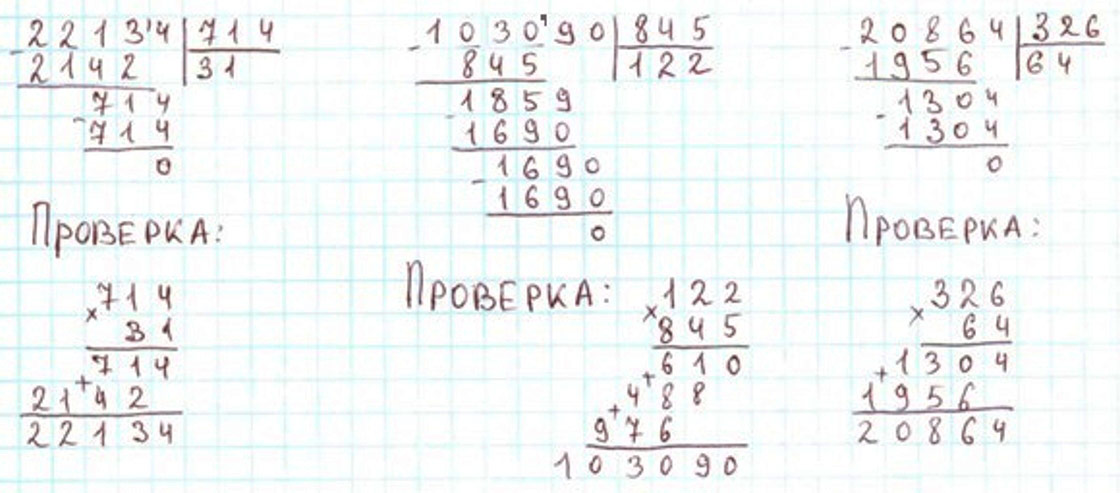
Номер 292.
Ответ:
Повтори алгоритм письменного деления и умножения на многозначные числа, а также порядок действий.
Выполняем вычисления с пояснениями.
Используя правило умножения числа на разность:
564 ∙ 70 – 564 ∙ 60 = 564 ∙ (70 – 60) = 564 ∙ 10 = 5 640
809 ∙ 62 + 809 ∙ 38 = 809 ∙ (62 + 38) = 809 ∙ 100 = 80 900
Рассуждаем далее:
Пишу: 68 432 : 94.
Разделю 68 432 на 94. Выделю первое неполное делимое – 684. Разделю 684 на 94, получу 7 – это пробная цифра.
Проверяю, подходит ли цифра 7.
Умножу 94 на 7, получу 658.
684 – 658 = 26. Добавляю 3 дес.
Нахожу вторую цифру частного:
263 : 94, получу 2.
Умножу 94 ∙ 2, получу 188.
263 – 188 = 75. Добавляю 2 ед.
Нахожу третью цифру частного:
752 : 94, получу 8.
Умножу 94 на 8, получу 752.
752 – 752 = 0.
Частное – 728.
Пишу: 20 706 : 67.
Разделю 20 706 на 67. Выделю первое неполное делимое – 207. Разделю 20 на 6, получу 3 – это пробная цифра.
Проверяю, подходит ли цифра 3.
Умножу 67 на 3, получу 201.
207 – 201 = 6. Добавляю 0 дес.
Нахожу вторую цифру частного:
60 : 67. 60 меньше, чем 67, пишу в частном 0. Добавляю 3 ед.
Нахожу третью цифру частного:
603 : 67, получу 9.
Умножу 67 на 9, получу 603.
603 – 603 = 0.
Частное – 309.
Пишу: 812 ∙ 907.
Умножу первый множитель на число единиц:
812 ∙ 7 = 5 684.
Получу первое неполное произведение: 5 684.
В десятках второго множителя – ноль, поэтому пропускаем этап умножения на десятки.
Умножу первый множитель на число сотен:
812 ∙ 9 = 7 308.
Получу второе неполное произведение: 7 308 сот.
Начну подписывать второе неполное произведение под сотнями.
Сложу неполные произведения.
Читаю ответ: 736 484. Это произведение чисел 812 и 907.
Пишу: 302 ∙ 470.
Ноль смещаем вправо и не учитываем его в умножении.
Умножу первый множитель на число единиц:
302 ∙ 7 = 2 114.
Получу первое неполное произведение: 2 114.
Умножу первый множитель на число десятков:
302 ∙ 4 = 1 208.
Получу второе неполное произведение: 1 208 дес.
Начну подписывать второе неполное произведение под десятками.
Сложу неполные произведения. Допишу к ответу ноль из второго множителя.
Читаю ответ: 141 940. Это произведение чисел 302 и 470.
Оформляем задание в тетрадь.
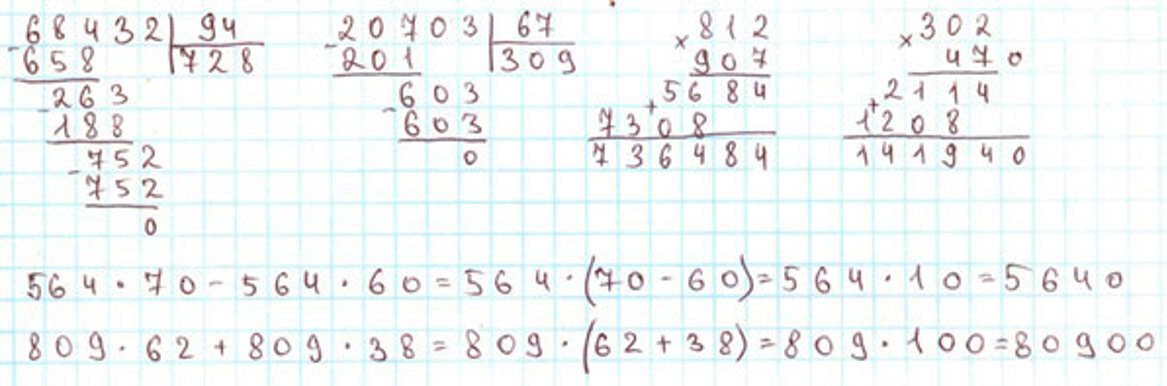
Номер 293.
Выполни чертёж и реши задачу.
Туристы прошли по реке на байдарках половину намеченного пути и ещё 9 км. Оставшийся путь они могут пройти на байдарках за 3 ч со скоростью 6 км/ч. Узнай весь путь, который должны были пройти туристы на байдарках.
1) 6 ∙ 3 = 18 (км) – осталось пройти туристам.
2) 18 + 9 = 27 (км) – половина намеченного пути.
3) 27 ∙ 2 = 54 (км) – длина всего маршрута, пройденного на байдарках.
Ответ: длина всего маршрута, пройденного на байдарках составляет 54 км.
Повтори взаимосвязь между скоростью, временем и расстоянием.
Оформляем условие в виде схематического чертежа.
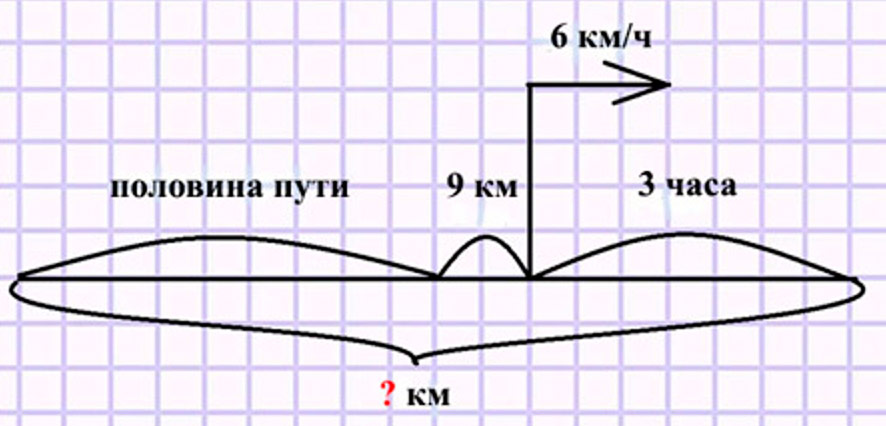
Рассуждаем.
Узнаем, сколько километров пути осталось пройти туристам. Для этого скорость движения умножим на время в пути.
1) 6 ∙ 3 = 18 (км) – осталось пройти туристам.
Продолжаем рассуждение.
Узнаем, сколько составляет половина намеченного пути.
2) 18 + 9 = 27 (км) – половина намеченного пути.
Продолжаем рассуждение.
Узнаем, сколько километров составит длина всего маршрута, пройденного на байдарках.
3) 27 ∙ 2 = 54 (км)
Записываем ответ.
Ответ: 54 км длина всего маршрута, пройденного на байдарках.
Номер 294.
Составь задачу по выражению 81 : 3 − 57 : 3.
Ответ:
Два автомобиля ехали 3 ч. Первый автомобиль проехал – 81 км, а второй – 57 км. На сколько больше скорость первого автомобиля, чем второго?
1) 81 : 3 − 57 : 3 = 27 − 19 = 8 (км/ч) – на столько скорость первого автомобиля больше, чем скорость второго автомобиля.
Ответ: на 8 км/ч больше скорость первого автомобиля, чем скорость второго автомобиля.
Повтори, что такое числовое выражение и случаи вне табличного деления.
Составим задачу по данному выражению.
Два автомобиля ехали 3 ч. Первый автомобиль проехал – 81 км, а второй – 57 км. На сколько больше скорость первого автомобиля, чем второго?
Оформляем условие в виде таблицы.
Рассуждаем.
Узнаем, на столько скорость первого автомобиля больше, чем скорость второго автомобиля.
1) 81 : 3 − 57 : 3 = 27 − 19 = 8 (км/ч)
Записываем ответ.
Ответ: на 8 км/ч скорость первого автомобиля больше, чем скорость второго автомобиля.
Номер 295.
В мастерской израсходовали 320 м шерстяной ткани и 340 м льняного полотна на пошив костюмов. Из шерстяной ткани сшили на 5 костюмов меньше, чем из льняного полотна. На каждый костюм расходовали одинаковое количество ткани. Сколько сшили костюмов из шерстяной ткани и сколько из льняного полотна?
Ответ:
1) 340 − 320 = 20 (м) – расход льняного полотна на 5 костюмов.
2) 20 : 5 = 4 (м) – расход льняного полотна на 1 костюм.
3) 320 : 4 = 80 (к.) – сшили из шерстяной ткани.
4) 340 : 4 = 85 (к.) – сшили из льняного полотна.
Ответ: 80 костюмов из шерстяной ткани и 85 костюмов из льняного полотна.
Повтори единицу длины – метр.
Оформляем условие в виде таблицы.
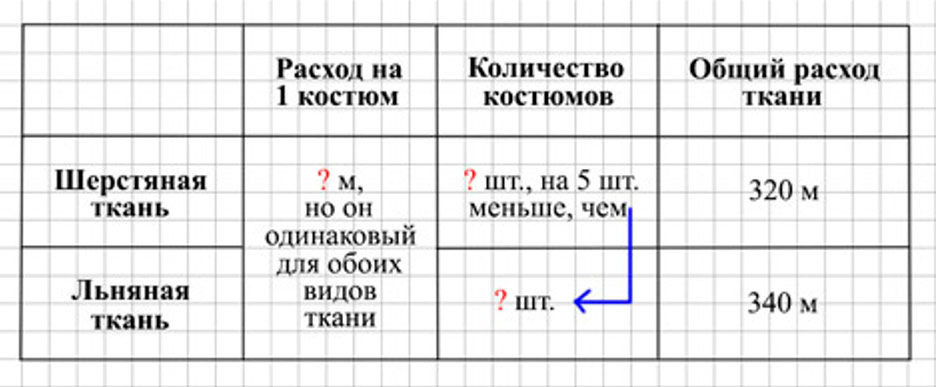
Рассуждаем.
Узнаем, каков расход льняного полотна на 5 костюмов.
1) 340 − 320 = 20 (м) – расход льняного полотна на 5 костюмов.
Продолжаем рассуждение.
Узнаем, каков расход льняного полотна на 1 костюм.
2) 20 : 5 = 4 (м) – расход льняного полотна на 1 костюм.
Продолжаем рассуждение.
Узнаем, сколько костюмов сшили из шерстяной ткани.
3) 320 : 4 = 80 (к.) – сшили из шерстяной ткани.
Продолжаем рассуждение.
Узнаем, сколько костюмов сшили из льняного полотна.
4) 340 : 4 = 85 (к.) – сшили из льняного полотна.
Записываем ответ.
Ответ: 80 и 85 костюмов.
Номер 296.
Составь по данным таблицы выражения и объясни, что они обозначают.
1) a : 6 (р.) − цена первого товара. 2) k : 4 (р.) − цена второго товара. 3) 20000 : b (р.) − цена третьего товара. 4) 40000 : c (р.) − цена четвертого товара. a + k + 20000 + 40000 = a + k + 60000 (р.) − стоимость всех покупок.
Повтори взаимосвязь между ценой, количеством и стоимостью.
Рассмотрим данные, приведенные в таблице.
Составим по данным таблицы выражения.
1) a : 6 (р.) − цена первого товара.
2) k : 4 (р.) − цена второго товара.
3) 20000 : b (р.) − цена третьего товара.
4) 40000 : c (р.) − цена четвертого товара.
a + k + 20000 + 40000 = a + k + 60000 (р.) − стоимость всех покупок.
Оформим задание в тетрадь.
Номер 297.
Сравни выражения.
Ответ:
84 : (6 ∙ 2) и 84 : 6 ∙ 2
84 : 6 : 2 < 14 ∙ 2
84 : 12 < 14 ∙ 2
7 < 28
Значит, 84 : (6 ∙ 2) < 84 : 6 ∙ 2
45 ∙ 12 и 45 ∙ 2 ∙ 6
45 ∙ 12 = 45 ∙ 12
540 = 540
Значит, 45 ∙ 12 = 45 ∙ 2 ∙ 6
18 ∙ 15 и 18 ∙ 10 + 5
270 > 180 + 5
270 > 185
Значит, 18 ∙ 15 > 18 ∙ 10 + 5
28 ∙ 9 и 20 ∙ 9 + 8 ∙ 9
(20 + 8) ∙ 9 = 20 ∙ 8 + 8 ∙ 9
20 ∙ 9 + 8 ∙ 9 = 20 ∙ 9 + 8 ∙ 9
180 + 72 = 180 + 72
252 = 252
Значит, 28 ∙ 9 = 20 ∙ 9 + 8 ∙ 9
Повтори, что такое неравенства.
Сравниваем выражения.
84 : (6 ∙ 2) и 84 : 6 ∙ 2
84 : 6 : 2 < 14 ∙ 2
84 : 12 < 14 ∙ 2
7 < 28
Значит, 84 : (6 ∙ 2) < 84 : 6 ∙ 2
45 ∙ 12 и 45 ∙ 2 ∙ 6
45 ∙ 12 = 45 ∙ 12
540 = 540
Значит, 45 ∙ 12 = 45 ∙ 2 ∙ 6
18 ∙ 15 и 18 ∙ 10 + 5
270 > 180 + 5
270 > 185
Значит, 18 ∙ 15 > 18 ∙ 10 + 5
28 ∙ 9 и 20 ∙ 9 + 8 ∙ 9
(20 + 8) ∙ 9 = 20 ∙ 8 + 8 ∙ 9
20 ∙ 9 + 8 ∙ 9 = 20 ∙ 9 + 8 ∙ 9
180 + 72 = 180 + 72
252 = 252
Значит, 28 ∙ 9 = 20 ∙ 9 + 8 ∙ 9
Оформляем задание в тетрадь.
84 : (6 ∙ 2) < 84 : 6 ∙ 2
45 ∙ 12 = 45 ∙ 2 ∙ 6
18 ∙ 15 > 18 ∙ 10 + 5
28 ∙ 9 = 20 ∙ 9 + 8 ∙ 9
Номер 298.
Площадь классной доски прямоугольной формы 288 дм², а её длина 24 дм. Найди ширину доски. Составь обратные задачи и реши их.
Ответ:
S = a ∙ b
Длина - 24 дм
S - 288 дм²
Ширина - ? дм
288 : 24 = 12 (дм) – ширина доски.
Ответ: ширина доски составляет 12 дм.
Обратная задача 1:
Длина классной доски 24 дм, а ширина – 12 дм. Найди её площадь.
S = a ∙ b
Длина - 24 дм
Ширина - 12 дм
S - ? дм²
24 ∙ 12 = 288 (дм²) – площадь доски.
Ответ: площадь доски составляет 288 дм².
Обратная задача 2:
Площадь классной доски прямоугольной формы 288 дм², а её ширина 12 дм. Найди длину доски.
S = a ∙ b
Ширина - 12 дм
S - 288 дм²
Длина - ? дм
288 : 12 = 24 (дм) – длина доски.
Ответ: длина доски составляет 24 дм.
Повтори, как найти площадь прямоугольника.
Шаг 1.
Оформляем условие в виде краткой записи.
S = a ∙ b
Длина – 24 дм
S – 288 дм²
Ширина – ? дм
Рассуждаем.
Найдем ширину доски, для этого площадь разделим на длину.
288 : 24 = 12 (дм)
Записываем ответ.
Ответ: 12 дм ширина доски.
Шаг 1.
Составляем первую задачу обратную данной.
Длина классной доски 24 дм, а ширина – 12 дм. Найди её площадь.
Оформляем условие в виде краткой записи.
S = a ∙ b
Длина – 24 дм
Ширина – 12 дм
S – ? дм²
Рассуждаем.
Найдем площадь доски, для этого длину доски умножим на ширину.
24 ∙ 12 = 288 (дм²)
Записываем ответ.
Ответ: 288 дм² площадь доски.
Шаг 1.
Составляем первую задачу обратную данной.
Площадь классной доски прямоугольной формы 288 дм², а её ширина 12 дм. Найди длину доски.
Оформляем условие в виде краткой записи.
S = a ∙ b
Ширина – 12 дм
S – 288 дм²
Длина – ? дм
Рассуждаем.
Найдем длину доски, для этого площадь доски разделим на ширину.
288 : 12 = 24 (дм)
Записываем ответ.
Ответ: 24 дм длина доски.
Задание внизу страницы
На склад привезли 4560 кг муки в мешках, по 80 кг в каждом, и 3840 кг крупы в мешках, по 60 кг в каждом. На сколько больше привезли мешков с крупой, чем с мукой?
Ответ:
1) 4560 : 80 = 57 (м.) – привезли на склад с мукой.
2) 3840 : 60 = 64 (м.) – привезли на склад с крупой.
3) 64 − 57 = 7 (м.) – на столько привезли на склад больше мешков с крупой, чем с мукой.
Ответ: на 7 мешков больше привезли на склад мешков с крупой, чем с мукой.
Повтори алгоритм письменного деления многозначных чисел.
Оформляем условие в виде таблицы.
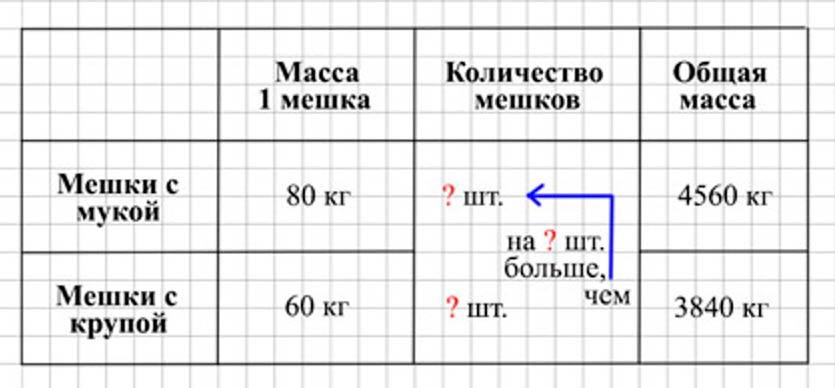
Рассуждаем.
Узнаем, сколько мешков по 80 кг привезли на склад с мукой.
1) 4560 : 80 = 57 (м.) – привезли на склад с мукой.
Продолжаем рассуждение.
Узнаем, сколько мешков по 60 кг привезли на склад с крупой.
2) 3840 : 60 = 64 (м.) – привезли на склад с крупой.
Продолжаем рассуждение.
Узнаем, на столько привезли на склад больше мешков с крупой, чем с мукой.
3) 64 − 57 = 7 (м.)
Записываем ответ.
Ответ: на 7 мешков на столько привезли на склад больше мешков с крупой, чем с мукой.
Задание на полях страницы
Цепочка.
Ответ:
9000 → 300 → 3 → 2400 → 240 → 720
Повтори, как умножать и делить на круглые числа.
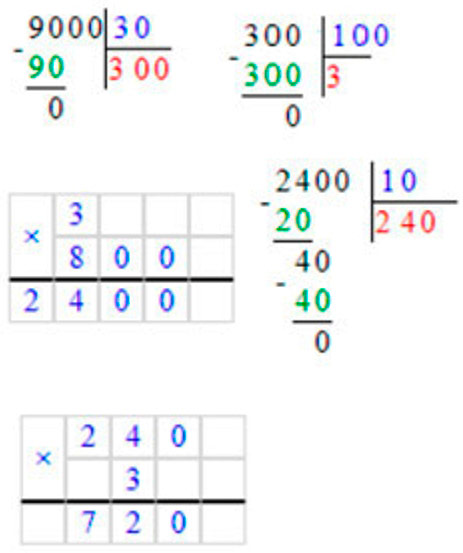
Выполняем вычисления по цепочке.
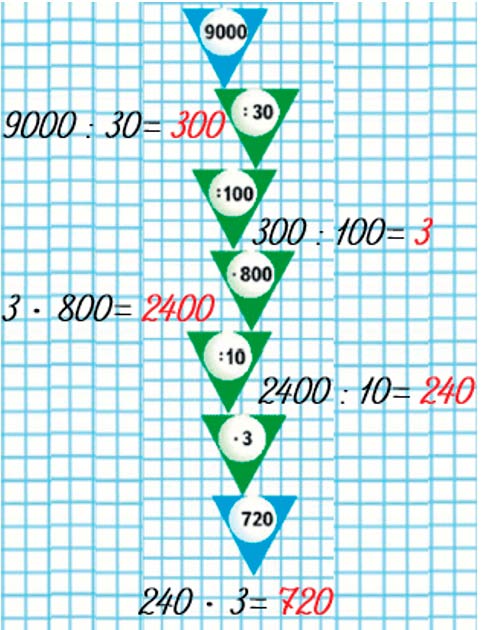
Оформляем задание в тетрадь.
9000 → 300 → 3 → 2400 → 240 → 720
Письменное деление на трёхзначное число
Номер 294.
1) Выполни деление с объяснением.
2) Объясняя так же, найди частное и остаток.
1)
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 74, номер 294, задание 1, 2024 год.")
Нужно разделить 954 на 318.
Чтобы легче было найти цифру частного, разделим 954 на 300.
Для этого разделим 9 на 3, в частном получим 3. Это пробная цифра, ее нужно проверить.
Умножим 318 на 3, получится 954.
Значит, частное 3.
Нужно разделить 876 на 219.
Чтобы легче было найти цифру частного, разделим 876 на 200.
Для этого разделим 8 на 2, в частном получим 4. Это пробная цифра, ее нужно проверить.
Умножим 219 на 4, получится 876.
Значит, частное 4.
Нужно разделить 2940 на 735.
Чтобы легче было найти цифру частного, разделим 2940 на 700.
Для этого разделим 29 на 7, в частном получим 4. Это пробная цифра, ее нужно проверить.
Умножим 735 на 4, получится 2940.
Значит, частное 4.
Нужно разделить 2544 на 424.
Чтобы легче было найти цифру частного, разделим 2544 на 400.
Для этого разделим 25 на 4, в частном получим 6. Это пробная цифра, ее нужно проверить.
Умножим 424 на 6, получится 2544.
Значит, частное 6.
2)
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 74, номер 294, задание 2, 2024 год.")
Нужно разделить 875 на 354. Чтобы легче было найти цифру частного разделим 875 на 300. Для этого разделим 8 на 3, в частном получим 2. Это пробная цифра, ее нужно проверить. Умножим 354 на 2, получится 708. Вычтем 708 и 875, получим 167. 167 - остаток. Проверка:
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 74, номер 294, пример 1, 2024 год.")
Значит, частное 2, остаток 167.
Нужно разделить 912 на 219.
Чтобы легче было найти цифру частного, разделим 912 на 200.
Для этого разделим 9 на 2, в частном получим 4. Это пробная цифра, ее нужно проверить.
Умножим 219 на 4, получится 876. Вычтем 876 из 912, получим 36.
36 − это остаток.
Проверка:
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 74, номер 294, пример 2, 2024 год.")
Значит, частное 4, остаток 36.
Нужно разделить 3964 на 526.
Чтобы легче было найти цифру частного, разделим 3964 на 500.
Для этого разделим 39 на 5, в частном получим 7. Это пробная цифра, ее нужно проверить.
Умножим 526 на 7, получится 3682. Вычтем 3682 из 3964, получим 282.
282 − это остаток.
Проверка:
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 74, номер 294, пример 3, 2024 год.")
Значит, частное 7, остаток 282.
Нужно разделить 2051 на 642.
Чтобы легче было найти цифру частного, разделим 2051 на 600.
Для этого разделим 20 на 6, в частном получим 3. Это пробная цифра, ее нужно проверить.
Умножим 642 на 3, получится 1926. Вычтем 1926 из 2051, получим 125.
125 − это остаток.
Проверка:
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 74, номер 294, пример 4, 2024 год.")
Значит, частное 3, остаток 125.
Номер 295.
На стройку привезли 120 т цемента, песка – в 2 раза больше, а щебёнки – в 4 раза больше, чем цемента. Для получения бетона израсходовали третью часть всех этих материалов. Поставь вопрос и реши задачу.
Ответ:Вариант 1: Сколько тонн привезенных материалов израсходовали для приготовления бетона?
1) 120 ∙ 2 = 240 (т) – песка привезли на стройку.
2) 120 ∙ 4 = 480 (т) – щебня привезли на стройку.
3) 480 + 120 + 240 = 840 (т) – масса всех материалов, которые привезли на стройку.
4) 840 : 3 = 280 (т) – материалов израсходовали для приготовления бетона.
Ответ: 280 т материалов всего израсходовали для приготовления бетона.
Вариант 2:
Сколько тонн привезенных материалов всего осталось?
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 74, номер 295, вариант 2, 2024 год.")
1) 120 ∙ 2 = 240 (т) – песка привезли на стройку.
2) 120 ∙ 4 = 480 (т) – щебня при везли на стройку.
3) 480 + 120 + 240 = 840 (т) – масса всех материалов, которые привезли на стройку.
4) 840 : 3 = 280 (т) – материалов израсходовали для приготовления бетона.
5) 840 − 280 = 560 (т) – материалов всего осталось неиспользованными.
Ответ: 560 т материалов всего осталось неиспользованными.
Номер 296.
На 21 детскую простыню требуется столько же полотна, сколько на 15 простыней для взрослых. Сколько полотна расходуют на 1 простыню для взрослых, если на 1 детскую простыню расходуют 1 м 50 см?
Ответ:
1 м 50 см = 150 см
1) 150 ∙ 21 = 3150 (см) – общий расход на изготовления 21 детской простыни или 15 взрослой.
2) 3150 : 15 = 210 (см) – полотна потребуется для одной взрослой простыни.
Ответ: 210 см = 2 м 10 см полотна потребуется для взрослой простыни.
Номер 297.
Составь по данному чертежу задачу и реши её.
Из двух пунктов одновременно навстречу друг другу выехали два автомобиля. Один ехал со скоростью 60 км/ч, а другой – 80 км/ч. Через 2 часа расстояние между ними стало равняться 420 км. Каково расстояние между пунктами, из которых выехали автомобили?
1) 60 + 80 = 140 (км/ч) – скорость сближения.
2) 140 ∙ 2 = 280 (км) – расстояние, пройденное автомобилями.
3) 420 + 280 = 700 (км) – расстояние между пунктами.
Ответ: расстояние между пунктами составляет 700 км.
Номер 298.
Ответ:
Задание внизу страницы
Вычисли.
Ответ:
Задание на полях страницы
Лабиринт.
Как выполнить это задание? Лабиринт - головоломка, в которой нужно найти верный путь, ведущий от начала лабиринта к центру. В данном случае ребенку предстоит решить математический лабиринт.
Над лабиринтом стоит значок (квадрат делить на квадрат). Он означает, что в данном лабиринте записаны: на внешнем круге - делимое, на втором круге - делитель, а в центре - частное. То есть ребенку нужно составить 4 примера, сочетающих такие комбинации чисел, чтобы каждый раз при делении получалось число 6.
Первый вариант:
Делимое – 420
Частное – 6
Значит, делитель – 70.
420 : 70 = 6
Второй вариант:
Делимое – 540
Частное – 6
Значит, делитель – 90.
540 : 90 = 6
Третий вариант:
Делимое – 360
Частное – 6
Значит, делитель – 60.
360 : 60=6
Четвертый вариант:
Делимое – 480
Частное – 6
Значит, делитель – 80.
480 : 80 = 6
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽
Напишите свой комментарий.