Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 72
- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Письменное деление на трёхзначное число
Номер 279.
1) Выполни деление с объяснением.
2) Объясняя так же, найди частное и остаток.
1)
.jpg "Изображение математика 4 класс Моро, Бантова - 2 часть страница 72, номер 279, задание 1")
Нужно разделить 954 на 318.
Чтобы легче было найти цифру частного, разделим 954 на 300.
Для этого разделим 9 на 3, в частном получим 3. Это пробная цифра, ее нужно проверить.
Умножим 318 на 3, получится 954.
Значит, частное 3.
Нужно разделить 876 на 219.
Чтобы легче было найти цифру частного, разделим 876 на 200.
Для этого разделим 8 на 2, в частном получим 4. Это пробная цифра, ее нужно проверить.
Умножим 219 на 4, получится 876.
Значит, частное 4.
Нужно разделить 2940 на 735.
Чтобы легче было найти цифру частного, разделим 2940 на 700.
Для этого разделим 29 на 7, в частном получим 4. Это пробная цифра, ее нужно проверить.
Умножим 735 на 4, получится 2940.
Значит, частное 4.
Нужно разделить 2544 на 424.
Чтобы легче было найти цифру частного, разделим 2544 на 400.
Для этого разделим 25 на 4, в частном получим 6. Это пробная цифра, ее нужно проверить.
Умножим 424 на 6, получится 2544.
Значит, частное 6.
2)
.jpg "Изображение математика 4 класс Моро, Бантова - 2 часть страница 72, номер 279, задание 2")
Нужно разделить 875 на 354. Чтобы легче было найти цифру частного разделим 875 на 300. Для этого разделим 8 на 3, в частном получим 2. Это пробная цифра, ее нужно проверить. Умножим 354 на 2, получится 708. Вычтем 708 и 875, получим 167. 167 - остаток. Проверка:
.jpg "Изображение математика 4 класс Моро, Бантова - 2 часть страница 72, номер 279, пример 1")
Значит, частное 2, остаток 167.
Нужно разделить 912 на 219.
Чтобы легче было найти цифру частного, разделим 912 на 200.
Для этого разделим 9 на 2, в частном получим 4. Это пробная цифра, ее нужно проверить.
Умножим 219 на 4, получится 876. Вычтем 876 из 912, получим 36.
36 − это остаток.
Проверка:
.jpg "Изображение математика 4 класс Моро, Бантова - 2 часть страница 72, номер 279, пример 2")
Значит, частное 4, остаток 36.
Нужно разделить 3964 на 526.
Чтобы легче было найти цифру частного, разделим 3964 на 500.
Для этого разделим 39 на 5, в частном получим 7. Это пробная цифра, ее нужно проверить.
Умножим 526 на 7, получится 3682. Вычтем 3682 из 3964, получим 282.
282 − это остаток.
Проверка:
.jpg "Изображение математика 4 класс Моро, Бантова - 2 часть страница 72, номер 279, пример 3")
Значит, частное 7, остаток 282.
Нужно разделить 2051 на 642.
Чтобы легче было найти цифру частного, разделим 2051 на 600.
Для этого разделим 20 на 6, в частном получим 3. Это пробная цифра, ее нужно проверить.
Умножим 642 на 3, получится 1926. Вычтем 1926 из 2051, получим 125.
125 − это остаток.
Проверка:
.jpg "Изображение математика 4 класс Моро, Бантова - 2 часть страница 72, номер 279, пример 4")
Значит, частное 3, остаток 125.
Повтори алгоритм письменного деления многозначных чисел на трёхзначные, а также как выполнять деление с остатком.
Выполняем деление с объяснением.
Нужно разделить 954 на 318.
Чтобы легче было найти цифру частного, разделим 954 на 300.
Для этого разделим 9 на 3, в частном получим 3. Это пробная цифра, ее нужно проверить.
Умножим 318 на 3, получится 954.
Значит, частное 3.
Нужно разделить 876 на 219.
Чтобы легче было найти цифру частного, разделим 876 на 200.
Для этого разделим 8 на 2, в частном получим 4. Это пробная цифра, ее нужно проверить.
Умножим 219 на 4, получится 876.
Значит, частное 4.
Нужно разделить 2940 на 735.
Чтобы легче было найти цифру частного, разделим 2940 на 700.
Для этого разделим 29 на 7, в частном получим 4. Это пробная цифра, ее нужно проверить.
Умножим 735 на 4, получится 2940.
Значит, частное 4.
Нужно разделить 2544 на 424.
Чтобы легче было найти цифру частного, разделим 2544 на 400.
Для этого разделим 25 на 4, в частном получим 6. Это пробная цифра, ее нужно проверить.
Умножим 424 на 6, получится 2544.
Значит, частное 6.
Находим частное и остаток.
Нужно разделить 875 на 354.
Чтобы легче было найти цифру частного разделим 875 на 300.
Для этого разделим 8 на 3, в частном получим 2. Это пробная цифра, ее нужно проверить.
Умножим 354 на 2, получится 708. Вычтем 708 и 875, получим 167.
167 – остаток.
Проверка:
1) 167 < 354
2) 2 ∙ 354 + 167 = 875
Значит, частное 2, остаток 167.
Нужно разделить 912 на 219.
Чтобы легче было найти цифру частного, разделим 912 на 200.
Для этого разделим 9 на 2, в частном получим 4. Это пробная цифра, ее нужно проверить.
Умножим 219 на 4, получится 876. Вычтем 876 из 912, получим 36.
36 − это остаток.
Проверка:
1) 36 < 219
2) 4 ∙ 219 + 36 = 912
Значит, частное 4, остаток 36.
Нужно разделить 3964 на 526.
Чтобы легче было найти цифру частного, разделим 3964 на 500.
Для этого разделим 39 на 5, в частном получим 7. Это пробная цифра, ее нужно проверить.
Умножим 526 на 7, получится 3682. Вычтем 3682 из 3964, получим 282.
282 − это остаток.
Проверка:
1) 282 < 526
2) 526 ∙ 7 + 282 = 3964
Значит, частное 7, остаток 282.
Нужно разделить 2051 на 642.
Чтобы легче было найти цифру частного, разделим 2051 на 600.
Для этого разделим 20 на 6, в частном получим 3. Это пробная цифра, ее нужно проверить.
Умножим 642 на 3, получится 1926. Вычтем 1926 из 2051, получим 125.
125 − это остаток.
Проверка:
1) 125 < 642
2) 3 ∙ 642 + 125 = 2051
Значит, частное 3, остаток 125.
Оформляем задание в тетрадь.
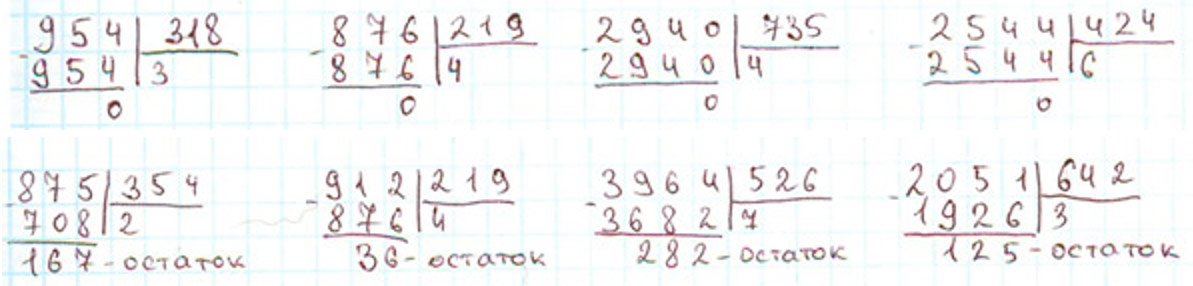
Номер 280.
На стройку привезли 120 т цемента, песка – в 2 раза больше, а щебёнки – в 4 раза больше, чем цемента. Для получения бетона израсходовали третью часть всех этих материалов. Поставь вопрос и реши задачу.
Ответ:Вариант 1: Сколько тонн привезенных материалов израсходовали для приготовления бетона?
1) 120 ∙ 2 = 240 (т) – песка привезли на стройку.
2) 120 ∙ 4 = 480 (т) – щебня привезли на стройку.
3) 480 + 120 + 240 = 840 (т) – масса всех материалов, которые привезли на стройку.
4) 840 : 3 = 280 (т) – материалов израсходовали для приготовления бетона.
Ответ: 280 тонн материалов всего израсходовали для приготовления бетона.
Вариант 2:
Сколько тонн привезенных материалов всего осталось?
.jpg "Изображение математика 4 класс Моро, Бантова - 2 часть страница 72, номер 280, вариант 2")
1) 120 ∙ 2 = 240 (т) – песка привезли на стройку.
2) 120 ∙ 4 = 480 (т) – щебня привезли на стройку.
3) 480 + 120 + 240 = 840 (т) – масса всех материалов, которые привезли на стройку.
4) 840 : 3 = 280 (т) – материалов израсходовали для приготовления бетона.
5) 840 − 280 = 560 (т) – материалов всего осталось неиспользованными.
Ответ: 560 т материалов всего осталось неиспользованными.
Повтори единицу массы – тонну, а также способы оформления краткой записи к задаче.
Поставим вопрос к задаче.
Сколько тонн привезенных материалов израсходовали для приготовления бетона?
Оформляем условие в виде.
Рассуждаем.
Узнаем, сколько песка привезли на стройку.
1) 120 ∙ 2 = 240 (т) – песка привезли на стройку.
Продолжаем рассуждение.
Узнаем, сколько щебня привезли на стройку.
2) 120 ∙ 4 = 480 (т) – щебня привезли на стройку.
Продолжаем рассуждение.
Узнаем массу всех материалов, которые привезли на стройку.
3) 480 + 120 + 240 = 840 (т) – масса всех материалов, которые привезли на стройку.
Продолжаем рассуждение.
Узнаем, сколько тонн всех материалов израсходовали для приготовления бетона.
4) 840 : 3 = 280 (т)
Записываем ответ.
Ответ: 280 тонн материалов израсходовали для приготовления бетона.
Номер 281.
На 21 детскую простыню требуется столько же полотна, сколько на 15 простыней для взрослых. Сколько полотна расходуют на 1 простыню для взрослых, если на 1 детскую простыню расходуют 1 м 50 см? (Вырази длину в сантиметрах.)
Ответ:
1 м 50 см = 150 см
1) 150 ∙ 21 = 3150 (см) – общий расход на изготовления 21 детской простыни или 15 взрослой.
2) 3150 : 15 = 210 (см) – полотна потребуется для одной взрослой простыни.
Ответ: 210 см = 2 м 10 см полотна потребуется для одной взрослой простыни.
Повтори алгоритм письменного умножения и деления на двузначные числа, а также единицы длины – сантиметр и метр.
Оформляем условие в виде таблицы.
Рассуждаем.
Узнаем, какой общий расход на изготовления 21 детской простыни или 15 взрослой.
1 м 50 см = 150 см
1) 150 ∙ 21 = 3150 (см) – общий расход на изготовления 21 детской простыни или 15 взрослой.
Продолжаем рассуждение.
Узнаем, сколько полотна потребуется для одной взрослой простыни.
2) 3150 : 15 = 210 (см) – полотна потребуется для одной взрослой простыни.
Записываем ответ.
Ответ:210 см = 2 м 10 см.
Номер 282.
Составь по данному чертежу задачу и реши её.
Из двух пунктов одновременно навстречу друг другу выехали два автомобиля. Один ехал со скоростью 60 км/ч, а другой – 80 км/ч. Через 2 часа расстояние между ними стало равняться 420 км. Каково расстояние между пунктами, из которых выехали автомобили?
1) 60 + 80 = 140 (км/ч) – скорость сближения.
2) 140 ∙ 2 = 280 (км) – расстояние, пройденное автомобилями.
3) 420 + 280 = 700 (км) – расстояние между пунктами.
Ответ: расстояние между пунктами составляет 700 км.
Повтори взаимосвязь между скоростью, временем и расстоянием.
Рассмотрим схематический чертеж.
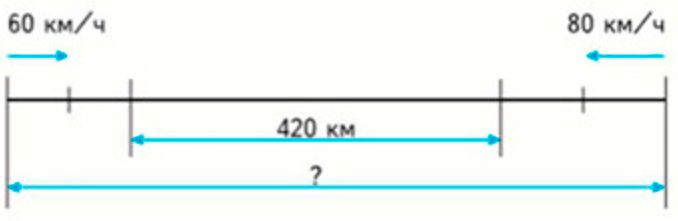
Составляем задачу по данным чертежа.
Из двух пунктов одновременно навстречу друг другу выехали два автомобиля. Один ехал со скоростью 60 км/ч, а другой – 80 км/ч. Через 2 часа расстояние между ними стало равняться 420 км. Каково расстояние между пунктами, из которых выехали автомобили?
Рассуждаем.
Найдем скорость сближения автомобилей.
1) 60 + 80 = 140 (км/ч) – скорость сближения.
Продолжаем рассуждение.
Найдем расстояние, которое прошли автомобили.
2) 140 ∙ 2 = 280 (км) – расстояние, пройденное автомобилями.
Продолжаем рассуждение.
Вычислим расстояние между пунктами.
3) 420 + 280 = 700 (км)
Записываем ответ.
Ответ: 700 км расстояние между пунктами.
Номер 283.
Ответ:
Повтори алгоритм письменного вычитания и умножения многозначных чисел, как умножать и делить круглые числа, а также порядок действий.
Выполняем вычисления по действиям.
Оформляем задание в тетрадь.
200 : 2 ∙ (540 + 460) : 10 = 10 000
200 : 2 ∙ 540 + 460 : 10 = 54 046
200 : 2 ∙ (540 + 460 : 10) = 58 600
1 200 – 200 : 40 ∙ 5 ∙ 5 = 1 075
1 200 – 200 : (40 ∙ 5) ∙ 5 = 1 195
(1 200 – 200 : 40) ∙ 5 ∙ 5 = 29 875
Задание внизу страницы
Вычисли.
Ответ:
Повтори алгоритм письменного деления многозначного числа на трёхзначное.
Выполняем вычисления с пояснениями.
Нужно разделить 2 072 : 518.
Чтобы легче было найти цифру частного, разделим 2 072 на 500.
Для этого разделим 20 на 5, в частном получим 4.
Это пробная цифра, её нужно проверить.
Умножим 518 на 4, получится 2 072. Значит, частное 4.
Оформляем задание в тетрадь.
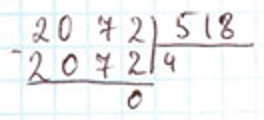
Задание на полях страницы
Лабиринт.
Как выполнить это задание? Лабиринт - головоломка, в которой нужно найти верный путь, ведущий от начала лабиринта к центру. В данном случае ребенку предстоит решить математический лабиринт.
Над лабиринтом стоит значок (квадрат делить на квадрат). Он означает, что в данном лабиринте записаны: на внешнем круге - делимое, на втором круге - делитель, а в центре - частное. То есть ребенку нужно составить 4 примера, сочетающих такие комбинации чисел, чтобы каждый раз при делении получалось число 6.
Первый вариант:
Делимое – 420
Частное – 6
Значит, делитель – 70.
420 : 70 = 6
Второй вариант:
Делимое – 540
Частное – 6
Значит, делитель – 90.
540 : 90 = 6
Третий вариант:
Делимое – 360
Частное – 6
Значит, делитель – 60.
360 : 60 = 6
Четвертый вариант:
Делимое – 480
Частное – 6
Значит, делитель – 80.
480 : 80 = 6
Повтори, как делить круглые числа.
Рассуждаем.
Как выполнить это задание? Лабиринт – головоломка, в которой нужно найти верный путь, ведущий от начала лабиринта к центру. В данном случае ребенку предстоит решить математический лабиринт.
Над лабиринтом стоит значок (квадрат делить на квадрат). Он означает, что в данном лабиринте записаны: на внешнем круге – делимое, на втором круге – делитель, а в центре – частное. То есть ребенку нужно составить 4 примера, сочетающих такие комбинации чисел, чтобы каждый раз при делении получалось число 6.
Выполняем вычисления.
Первый вариант:
Делимое – 420
Частное – 6
Значит, делитель – 70.
420 : 70 = 6
Второй вариант:
Делимое – 540
Частное – 6
Значит, делитель – 90.
540 : 90 = 6
Третий вариант:
Делимое – 360
Частное – 6
Значит, делитель – 60.
360 : 60 = 6
Четвертый вариант:
Делимое – 480
Частное – 6
Значит, делитель – 80.
480 : 80 = 6
Оформляем задание в тетрадь.
420 : 70 = 6
540 : 90 = 6
360 : 60 = 6
480 : 80 = 6
Номер 11.
Реши уравнения.
Ответ:
х + 287 = 486
х = 486 − 287
х = 199
Проверка:
199 + 287 = 486
486 = 486
Ответ: х = 199
403 − х = 265
х = 403 − 265
х = 138
Проверка:
403 − 138 = 265
265 = 265
Ответ: х = 138
х − 288 = 513
х = 513 + 288
х = 801
Проверка:
801 − 288 = 513
513 = 513
Ответ: х = 801
х : 11 = 22033
х = 22033 ∙ 11
х = 242363
Проверка:
242363 : 11 = 22033
22033 = 22033
Ответ: х = 242363
725 : х = 29
х = 725 : 29
х = 25
Проверка:
725 : 25 = 29
29 = 29
Ответ: х = 29
47 ∙ х = 4700
х = 4700 : 47
х = 100
Проверка:
47 ∙ 100 = 4700
4700 = 4700
Ответ: х = 100
Повтори, как решать уравнения.
Выполняем вычисления.
х + 287 = 486
Чтобы найти первое слагаемое, нужно из суммы вычесть второе слагаемое.
х = 486 – 287
х = 199
Проверка:
199 + 287 = 486
486 = 486
х : 11 = 22033
Чтобы найти делимое, нужно частное умножить на делитель.
х = 22033 ∙ 11
х = 242363
Проверка:
242363 : 11 = 22033
22033 = 22033
403 – х = 265
Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.
х = 403 – 265
х = 138
Проверка:
403 – 138 = 265
265 = 265
725 : х = 29
Чтобы найти делитель, нужно делимое разделить на частное.
х = 725 : 29
х = 25
Проверка:
725 : 25 = 29
29 = 29
х – 288 = 513
Чтобы найти уменьшаемое, нужно к разности прибавить вычитаемое.
х = 513 + 288
х = 801
Проверка:
801 – 288 = 513
513 = 513
47 ∙ х = 4700
Чтобы найти второй множитель, нужно произведение разделить на первый множитель.
х = 4700 : 47
х = 100
Проверка:
47 ∙ 100 = 4700
100 = 100
Оформляем задание в тетрадь.
х + 287 = 486
х = 486 − 287
х = 199
Проверка:
199 + 287 = 486
486 = 486
403 − х = 265
х = 403 − 265
х = 138
Проверка:
403 − 138 = 265
265 = 265
х − 288 = 513
х = 513 + 288
х = 801
Проверка:
801 − 288 = 513
513 = 513
х : 11 = 22033
х = 22033 ∙ 11
х = 242363
Проверка:
242363 : 11 = 22033
22033 = 22033
725 : х = 29
х = 725 : 29
х = 25
Проверка:
725 : 25 = 29
29 = 29
47 ∙ х = 4700
х = 4700 : 47
х = 100
Проверка:
47 ∙ 100 = 4700
4700 = 4700
Номер 12.
Площадь участка, занятого пшеницей, 1200 м². С каждых 100 м² этого участка собрали по 48 кг зерна. Сколько килограммов зерна собрали со всего этого участка?
Ответ:
Площадь участка – 1200 м²
Собрали с 100 м² – 48 кг
Собрали со всего участка – ? кг
1) 1200 : 100 = 12 (раз) – по 100 м² содержится в 1200 м².
2) 48 ∙ 12 = 576 (кг) – зерна собрали со всего участка.
Ответ: 576 кг зерна собрали со всего участка.
Повтори единицу массы — килограмм и единицы площади.
Оформляем условие в виде краткой записи.
Площадь участка — 1200 м²
Собрали с 100 м² — 48 кг
Собрали со всего участка — ? кг
Рассуждаем.
Вычислим, сколько раз по 100 м² содержится на данном участке.
1200 : 100 = 12 (раз) — по 100 м² содержится в 1200 м².
Продолжаем рассуждение.
Узнаем, сколько зерна собрали со всего участка.
48 ∙ 12 = 576 (кг) — зерна собрали со всего участка.
Записываем ответ.
Ответ: 576 кг зерна всего собрали.
Номер 13.
Какой длины могут быть стороны прямоугольника, площадь которого 600 мм²? Начерти три таких прямоугольника, найди периметр каждого из них.
Ответ:
Первый вариант:
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 72, номер 13, вариант 1, 2024 год")
S = 60 ∙ 10 = 600 (мм²)
Р = (60 + 10) ∙ 2 = 70 ∙ 2 = 140 (мм)
Второй вариант:
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 72, номер 13, вариант 2, 2024 год")
S = 20 ∙ 30 = 600 (мм²)
Р = (20 + 30) ∙ 2 = 50 ∙ 2 = 100 (мм)
Третий вариант:
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 72, номер 13, вариант 3, 2024 год")
S = 15 ∙ 40 = 600 (мм²)
Р = (15 + 40) ∙ 2 = 55 ∙ 2 = 110 (мм)
Ответ: стороны могут быть: 10 мм и 60 мм; 20 мм и 30 мм; 15 мм и 40 мм.
Повтори, как найти площадь и периметр прямоугольника, а также единицу длины — миллиметр.
Первый вариант.
S = 60 ∙ 10 = 600 (мм²)
Р = (60 + 10) ∙ 2 = 70 ∙ 2 = 140 (мм)
Второй вариант.
S = 20 ∙ 30 = 600 (мм²)
Р = (20 + 30) ∙ 2 = 50 ∙ 2 = 100 (мм)
Третий вариант.
S = 15 ∙ 40 = 600 (мм²)
Р = (15 + 40) ∙ 2 = 55 ∙ 2 = 110 (мм)
Записываем ответ.
Ответ:
1) стороны — 60 мм и 10 мм, периметр — 140 мм.
2) стороны — 20 мм и 30 мм, периметр — 100 мм.
3) стороны — 15 мм и 40 мм, периметр — 110 мм.
Номер 14.
Сравни.
Ответ:
5321 см и 53 м 21 см
53 м 21 см = 53 ∙ 100 + 21 = 5300 + 21 = 5321 см
5321 см = 5321 см
Значит, 5321 см = 53 м 21 см
7080 см и 708 дм
708 дм = 708 ∙ 10 = 7080 см
7080 см = 7080 см
Значит, 7080 см = 708 дм
2 м² и 1000 см²
2 м² = 2 ∙ 100 ∙ 100 = 20000 см²
20000 см² > 1000 см²
Значит, 2 м² > 1000 см²
7910 ц и 79 т 1 ц
79 т 1ц = 79 ∙ 10 + 1 = 791 ц
7910 ц > 791 ц
Значит, 7910 ц > 79 т 1 ц
3600 с и 6 мин
6 мин = 6 ∙ 60 = 360 сек
3600 с > 360 с
Значит, 3600 с > 6 мин
425 мин и 7 ч
7 ч = 7 ∙ 60 = 420 мин
425 мин > 420 мин
Значит, 425 мин > 7 ч
Повтори единицы длины — метр, дециметр и сантиметр, единицы массы — тонну и центнер, единицы времени — час, минуту и секунду, а также единицы площади.
Выполняем вычисления.
Сравним 5321 см и 53 м 21 см
Так как 1 м = 100 см, то
53 м 21 см = 53 ∙ 100 + 21 = 5300 + 21 = 5321 см
5321 см = 5321 см
Значит, 5321 см = 53 м 21 см
Сравним 7080 см и 708 дм
Так как 1 дм = 10 см, то
708 дм = 708 ∙ 10 = 7080 см
7080 см = 7080 см
Значит, 7080 см = 708 дм
Сравним 2 м² и 1000 см²
Так как 1 м² = 10000 см², то
2 м² = 2 ∙ 100 ∙ 100 = 20000 см²
20000 см² > 1000 см²
Значит, 2 м² > 1000 см²
Сравним 7910 ц и 79 т 1 ц
Так как 1 т = 10 ц, то
79 т 1 ц = 79 ∙ 10 + 1 = 791 ц
7910 ц > 791 ц
Значит, 7910 ц > 79 т 1 ц
Сравним 3600 с и 6 мин
Так как 1 мин = 60 с, то
6 мин = 6 ∙ 60 = 360 с
3600 с > 360 с
Значит, 3600 с > 6 мин
Сравним 425 мин и 7 ч
Так как 1 ч = 60 мин, то
7 ч = 7 ∙ 60 = 420 мин
425 мин > 420 мин
Значит, 425 мин > 7 ч
Оформляем задание в тетрадь.
5321 см = 53 м 21 см
7080 см = 708 дм
2 м² > 1000 см²
7910 ц > 79 т 1 ц
3600 с > 6 мин
425 мин > 7 ч
Номер 15.
Объясни, какие ошибки допустил ученик, выполняя деление, и запиши правильное решение.
Ответ:
1) При делении 40160 на 80 ученик допустил ошибку в разряде десятков частного. Он пропустил нуль и получил ответ 52, а не 502.
2) При делении 18288 на 36 была допущена ошибка при нахождении первого неполного делимого. 182 разделили на 36 и взяли не максимально возможное число (4, а не 5) и из-за этого деление пошло неверным путем, ведь первым неполным делимым стало число, которое больше делителя, а значит можно было взять число, на которое делили 182 больше, чем 4 и это - 5.
Повтори алгоритм письменного деления на двузначные числа.
Рассмотрим примеры.
Найдем ошибки.
1) При делении 40160 на 80 ученик допустил ошибку в разряде десятков частного. Он пропустил нуль и получил ответ 52, а не 502. Так как второе неполное делимое — 16, которое меньше 80, значит в частном в разряде десятков 0.
2) При делении 18288 на 36 была допущена ошибка при нахождении первого неполного частного. 182 разделили на 36 и получили 4, при этом остаток — 38, который больше делителя 36. Значит, первое неполное частное не 4, а 5.
Решим примеры.
Номер 16.
Реши задачи. Чем похожи решения задач? Чем различаются?
1) На двух опытных участках общей площадью 100 м² высадили тюльпаны. На каждом квадратном метре высаживали одинаковое число луковиц. На первом участке посадили 960 луковиц, а на втором – 640 луковиц. Чему равна площадь каждого участка?
2) На двух опытных высадили тюльпаны: на одном 960 луковиц, на другом 640 луковиц. На каждом квадратном метре высаживали одинаковое число луковиц. Площадь первого участка была на 20 м² больше, чем площадь второго. Чему равна площадь каждого участка?
Задача 1:
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 72, номер 16, задача 1, 2024 год")
1) 960 + 640 = 1600 (лук.) – посадили на двух участках.
2) 1600 : 100 = 16 (лук.) – на 1 м².
3) 960 : 16 = 60 (м²) – площадь первого участка.
4) 100 − 60 = 40 (м²) – площадь второго участка.
Ответ: площадь первого участка составляет 60 м², площадь второго участка составляет 40 м².
Задача 2:
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 72, номер 16, задача 2, 2024 год")
1) 960 − 640 = 320 (лук.) – на столько больше посадили на первом участке, чем на втором.
2) 320 : 20 = 16 (лук.) – расход на 1 м².
3) 960 : 16 = 60 (м²) – площадь первого участка.
4) 100 − 60 = 40 (м²) – площадь второго участка.
Ответ: площадь первого участка составляет 60 м², площадь второго участка составляет 40 м².
Сравнение задач и их решений:
Обе задачи содержат информацию о количестве луковиц, посаженных на 1 и 2 участках. Дополнительной информацией в первой задаче является общая площадь двух участков, а во второй - на сколько площадь 1 участка больше второго.
Что касается действий, то в первой задаче мы сначала ищем сколько всего луковиц посадили на обоих участках, и делим на сумму площадей, чтобы найти расход на 1 м², а во второй ищем разность между количествами высаженных луковиц, чтобы потом разделить полученное число на разность площадей и найти расход на 1 м².
Далее мы ищем площади участков. В обеих задачах мы делим на расход на 1 м² число посаженных на первом участке луковиц, посаженных на втором участке и находим площади участков.
Повтори единицы площади.
Шаг 1.
Оформляем условие в виде таблицы.
Рассуждаем.
Узнаем, сколько луковиц тюльпана посадили на двух участках.
960 + 640 = 960 + 40 + 600 = 1000 + 600 = 1600 (лук.) — тюльпана посадили на двух участках.
Продолжаем рассуждение.
Узнаем, сколько луковиц тюльпана высадили на 1 м².
1600 : 100 = 16 (лук.) — тюльпана высадили на 1 м².
Продолжаем рассуждение.
Найдем площадь первого участка.
960 : 16 = 60 (м²) — площадь первого участка.
Продолжаем рассуждение.
Найдем площадь второго участка.
100 − 60 = 40 (м²) — площадь второго участка.
Записываем ответ.
Ответ: площадь первого участка равна 60 м² , второго — 40 м².
Шаг 1.
Оформляем условие в виде таблицы.
Рассуждаем.
Узнаем, на сколько больше луковиц тюльпана посадили на первом участке, чем на втором.
960 − 640 = 320 (лук.) — на столько больше посадили на первом участке, чем на втором.
Продолжаем рассуждение.
Узнаем, сколько луковиц тюльпана высадили на 1 м².
320 : 20 = 16 (лук.) — тюльпана высадили на 1 м².
Продолжаем рассуждение.
Найдем площадь первого участка.
960 : 16 = 60 (м²) — площадь первого участка.
Продолжаем рассуждение.
Найдем площадь второго участка.
60 – 20 = 40 (м²) — площадь второго участка.
Записываем ответ.
Ответ: площадь первого участка равна 60 м² , второго — 40 м².
Сравниваем задачи их решения.
Обе задачи содержат информацию о количестве луковиц, посаженных на 1 и 2 участках. Дополнительной информацией в первой задаче является общая площадь двух участков, а во второй — на сколько площадь первого участка больше второго.
Что касается действий, то в первой задаче мы сначала ищем сколько всего луковиц посадили на обоих участках, и делим на сумму площадей, чтобы найти количество луковиц, высаженных на 1 м², а во второй ищем разность между количеством высаженных луковиц на участках, чтобы потом разделить полученное число на разность площадей и найти количество луковиц, высаженных на 1 м². Далее мы ищем площади участков. В обеих задачах мы делим общее количество луковиц на количество луковиц, высаженных на 1 м², и находим площади участков.
Номер 17.
Из 50 кг молока получается 4 кг сыра. Сколько килограммов сыра получится из 1 т молока? из 5 т?
Ответ:50 кг молока – 4 кг сыра 1 т молока – ? кг сыра 5 т молока – ? кг сыра
1 т = 1000 кг
5 т = 5000 кг
5000 кг молока в 5 раз больше, чем 1000 кг молока, значит и сыра будет в 5 раз больше из 5000 кг молока, чем из 1000 кг.
1) 1000 : 50 = 20 (раз) – во столько раз 1 т больше 50 кг.
2) 4 ∙ 20 = 80 (кг) – сыра получается из 1 т молока.
3) 80 ∙ 5 = 400 (кг) – сыра получается из 5 т молока.
1 т = 1000 кг
5 т = 5000 кг
1) 1000 : 50 = 20 (раз) – во столько раз 1 т больше 50 кг.
Во сколько раз молока больше, во столько раз и сыра получится больше.
2) 4 ∙ 20 = 80 (кг) – сыра получается из 1 т молока.
3) 5000 : 50 = 100 (раз) – во столько 5 тонн молока больше, чем 50 кг молока.
Во сколько раз молока больше, во столько раз и сыра получится больше.
4) 80 ∙ 5 = 400 (кг) – сыра получается из 5 т молока.
Ответ: 80 кг сыра всего получается из 1 т молока, 400 кг сыра всего получается из 5 т молока.
Повтори единицы массы — тонну и килограмм.
Оформляем условие в виде краткой записи.
Из 50 кг молока — 4 кг сыра
Из 1 т молока — ? кг сыра
Из 5 т молока — ? кг сыра
Рассуждаем.
Узнаем, во сколько раз 1 тонна молока больше, чем 50 кг молока.
Так как 1 т = 1000 кг, то
1000 : 50 = 20 (раз) — во столько раз 1 т больше 50 кг.
Продолжаем рассуждение.
Теперь можем узнать, сколько получится сыра. Во сколько раз молока больше, во столько раз и сыра получится больше.
4 ∙ 20 = 80 (кг) — сыра получится из 1 т молока.
Продолжаем рассуждение.
Узнаем, во сколько 5 тонн молока больше, чем 50 кг молока.
Так как 5 т = 5000 кг, то
5000 : 50 = 100 (раз) — во столько раз 5 тонн молока больше, чем 50 кг молока.
Продолжаем рассуждение.
Во сколько раз молока больше, во столько раз и сыра получится больше.
4 ∙ 100 = 400 (кг) — сыра получается из 5 т молока.
Записываем ответ.
Ответ: 80 кг сыра получится из 1 т молока, 400 кг сыра — из 5 т молока.
Задание на полях страницы
Ребус.
Перед нами ребус, для того чтобы найти недостающие цифры необходимо выполнить деление.
Рассмотрим ребус.
Разгадаем ребус.
Какое двузначное число с 5 десятками можно разделить на 7 без остатка? Это число 56. 56 : 7 = 8. Пишу 8 в частном.
Какое двузначное число с 5 единицами можно разделить на 7 без остатка? Это число 35.
Так как 3 < 7, то пишем в частном 0.
35 : 7 = 5. Пишу 5 в частном.
Оформим задание в тетрадь.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽
Напишите свой комментарий.