Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 71
- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
.jpg "Математика 4 класс Моро, Волкова - 2 часть страница 71")
Номер 18.
Ответ:
Повтори алгоритм письменного умножения и деления на двузначные числа, а также порядок действий.
Выполняем вычисления по действиям.
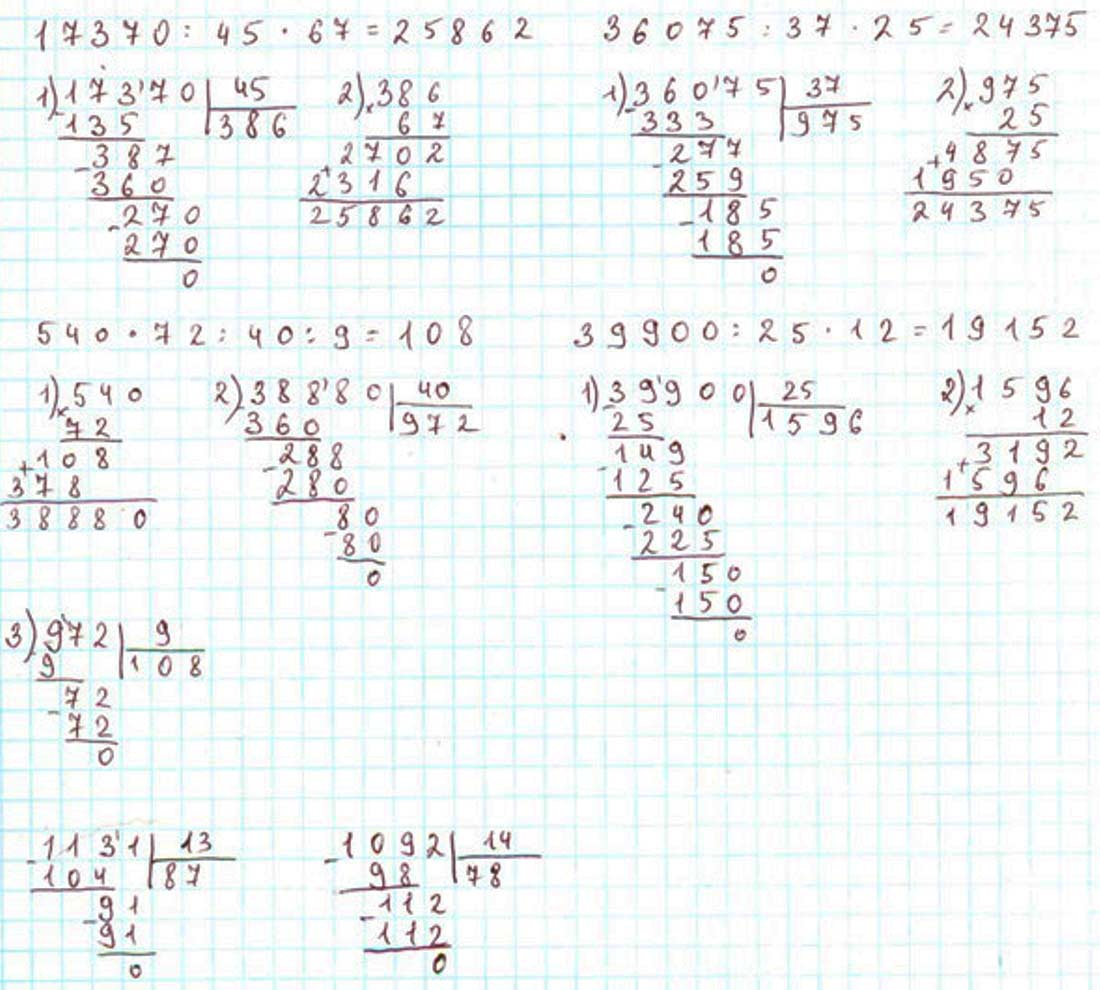
Оформляем задание в тетрадь.
17 370 : 45 ∙ 67 = 25 862
540 ∙ 72 : 40 : 9 = 108
36 075 : 37 ∙ 25 = 24 375
39 900 : 25 ∙ 12 = 19 152
Номер 19.
Квартал – четвёртая часть года. Сколько месяцев в одном квартале? Сколько дней в последнем квартале года?
Ответ:
12 : 4 = 3 (мес.) – в каждом квартале.
В последнем квартале 3 месяца: октябрь, ноябрь, декабрь.
Октябрь – 31 день
Ноябрь – 30 дней
Декабрь – 31 день
31 + 30 + 31 = 92 (дня)
Ответ: 3 месяца всего в последнем квартале года; 92 дня всего в последнем квартале года.
Повтори единицы времени – год и месяц.
Рассмотрим чертеж на полях страницы.
Рассуждаем.
Узнаем, сколько месяцев с одном квартале.
12 : 4 = 3 (мес.) – в каждом квартале.
Продолжаем рассуждение.
В последнем квартале 3 месяца: октябрь, ноябрь, декабрь.
Октябрь – 31 день
Ноябрь – 30 дней
Декабрь – 31 день
31 + 30 + 31 = 92 (дня)
Записываем ответ.
Ответ: 3 месяца; 92 дня.
Номер 20.
На изготовление 10 пар детских ботинок потребовалось 36 дм² кожи. Сколько квадратных метров кожи потребуется на 1000 пар таких ботинок?
Ответ:
10 пар – 36 дм² кожи
1000 пар – ? м² кожи
1 м² = 100 дм²
1) 1000 : 10 = 100 (раз) – во столько раз больше пар обуви сделали из неизвестного количества кожи, чем из 36 дм².
2) 36 ∙ 100 = 3600 дм² = 36 м² (кожи) – понадобятся для изготовления 1000 пар ботинок.
Ответ: 36 м² кожи понадобится для изготовления 1000 пар ботинок.
Повтори единицы площади.
Оформляем условие в виде краткой записи.
10 пар – 36 дм² кожи
1000 пар – ? м² кожи
Рассуждаем. Переведем квадратные метры в квадратные дециметры.
Узнаем, во сколько раз больше пар обуви сделали из неизвестного количества кожи, чем 36 дм².
1 м² = 100 дм²
1) 1000 : 10 = 100 (раз) – во столько раз больше пар обуви сделали из неизвестного количества кожи, чем из 36 дм².
Продолжаем рассуждение.
Узнаем, сколько квадратных метров кожи потребуется для изготовления 1000 пар ботинок.
2) 36 ∙ 100 = 3600 дм² = 36 м² (кожи) – понадобятся для изготовления 1000 пар ботинок.
Записываем ответ.
Ответ: 36 м².
Номер 21.
1) От двух пристаней, находящихся на расстоянии 510 км, отплыли в 7 ч навстречу друг другу катер и моторная лодка. Встреча произошла в 24 ч этого же дня. Катер шёл со скоростью 19 км/ч. С какой скоростью шла лодка?
2) На каком расстоянии друг от друга находились катер и лодка через 3 ч после встречи? Сделай по задаче чертёж и реши задачу.
Задача 1:
.jpg "Изображение математика 4 класс Моро, Бантова - 2 часть страница 71, номер 21, задача 1")
1) 24 − 7 = 17 (ч) – были в пути лодка и катер до встречи.
2) 510 : 17 = 30 (км/ч) – скорость сближения транспорта.
3) 30 − 19 = 11 (км/ч) – скорость моторной лодки.
Ответ: скорость моторной лодки составляет 11 км/ч.
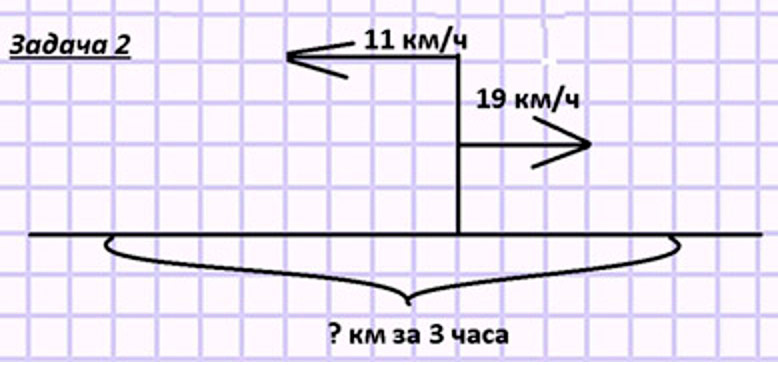
Задача 2:
.jpg "Изображение математика 4 класс Моро, Бантова - 2 часть страница 71, номер 21, задача 2")
Нам нужно найти расстояние через 3 часа после встречи.
Лодка и катер встретились, но продолжили движения и идут каждый в свою сторону, то есть теперь они удаляются друг от друга. И нужно найти расстояние между ними через 3 часа удаления.
1) 19 + 11 = 30 (км/ч) – скорость удаления.
2) 30 ∙ 3 = 90 (км) – расстояние между катером и лодкой через 3 часа движения.
Ответ: расстояние между катером и лодкой через 3 часа движения составит 90 км.
Повтори взаимосвязь между скоростью, временем и расстоянием.
Шаг 1.
Оформляем условие в виде схематического чертежа.
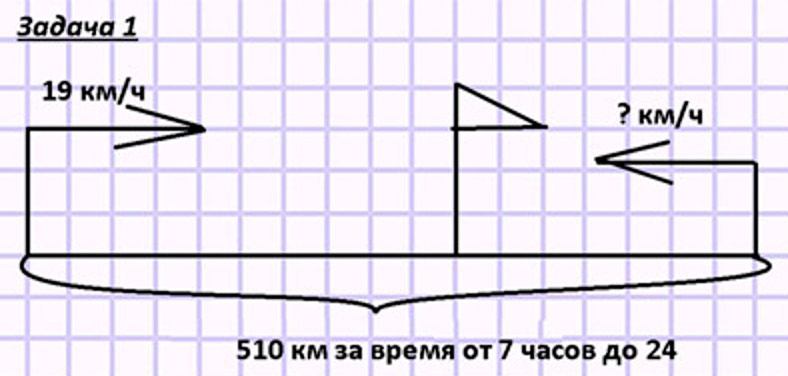
Рассуждаем.
Узнаем, сколько времени в пути были лодка и катер до встречи.
1) 24 − 7 = 17 (ч) – были в пути лодка и катер до встречи.
Продолжаем рассуждение.
Узнаем, скорость сближения лодки и катера.
2) 510 : 17 = 30 (км/ч) – скорость сближения транспорта.
Продолжаем рассуждение.
Узнаем, скорость моторной лодки. Для этого из скорости сближения транспорта вычтем скорость катера.
3) 30 − 19 = 11 (км/ч) – скорость моторной лодки.
Записываем ответ.
Ответ: 11 км/ч.
Шаг 1.
Оформляем условие в виде схематического чертежа.
Рассуждаем.
Нам нужно найти расстояние через 3 часа после встречи.
Лодка и катер встретились, но продолжили движения и идут каждый в свою сторону, то есть теперь они удаляются друг от друга. И нужно найти расстояние между ними через 3 часа удаления.
Продолжаем рассуждение.
1) 19 + 11 = 30 (км/ч) – скорость удаления.
2) 30 ∙ 3 = 90 (км) – расстояние между катером и лодкой через 3 часа движения.
Записываем ответ.
Ответ: 90 км.
Номер 22.
Длина участка земли прямоугольной формы 25 м, а ширина 24 м. Десятую часть этого участка занимают постройки. На четвёртой его части посажены овощи, а на остальной площади – фруктовые деревья. Какая площадь занята фруктовыми деревьями?
Ответ:
1) 25 ∙ 24 = 600 (м²) – площадь участка.
2) 600 : 10 = 60 (м²) – площадь земли, занятой постройками.
3) 600 : 4 = 150 (м²) – площадь земли, занятой овощами.
4) 150 + 60 = 210 (м²) – площадь земли, занятой постройками и овощами вместе.
5) 600 − 210 = 390 (м²) – площадь земли, занятая фруктовыми деревьями.
Ответ: площадь земли, занятая фруктовыми деревьями составляет 390 м².
Повтори, как найти площадь прямоугольника, что такое доли и способы оформления краткой записи к задаче.
Оформляем условие в виде краткой записи.
Рассуждаем.
Найдем площадь участка.
1) 25 ∙ 24 = 600 (м²) – площадь участка.
Продолжаем рассуждение.
Найдем площадь земли занятой постройками.
2) 600 : 10 = 60 (м²) – площадь земли, занятой постройками.
Продолжаем рассуждение.
Найдем площадь земли занятой овощами.
3) 600 : 4 = 150 (м²) – площадь земли, занятой овощами.
Продолжаем рассуждение.
Найдем площадь земли, занятой постройками и овощами вместе.
4) 150 + 60 = 210 (м²) – площадь земли, занятой постройками и овощами вместе.
Продолжаем рассуждение.
Найдем площадь земли, занятой фруктовыми деревьями.
5) 600 − 210 = 390 (м²) – площадь земли, занятая фруктовыми деревьями.
Записываем ответ.
Ответ: 390 м².
Номер 23.
Один грузовик может вывезти с поля 840 т зерна за 60 ч, а другой – тот же груз за 84 ч. Сколько на это потребуется времени при совместной работе обоих грузовиков?
Ответ:
1) 840 : 60 = 14 (т) – зерна перевозит первый грузовик за 1 час.
2) 840 : 84 = 10 (т) – зерна перевозит второй грузовик за 1 час.
3) 14 + 10 = 24 (т) – зерна перевозят оба грузовика за 1 час.
4) 840 : 24 = 35 (ч) – потребуется грузовикам при совместной работе, чтобы перевезти 840 т зерна.
Ответ: 35 часов всего потребуется, чтобы перевезти 840 т зерна.
Повтори единицу времени – час, единицу массы – тонну, а также алгоритм письменного деления круглого числа.
Оформляем условие в виде таблицы.
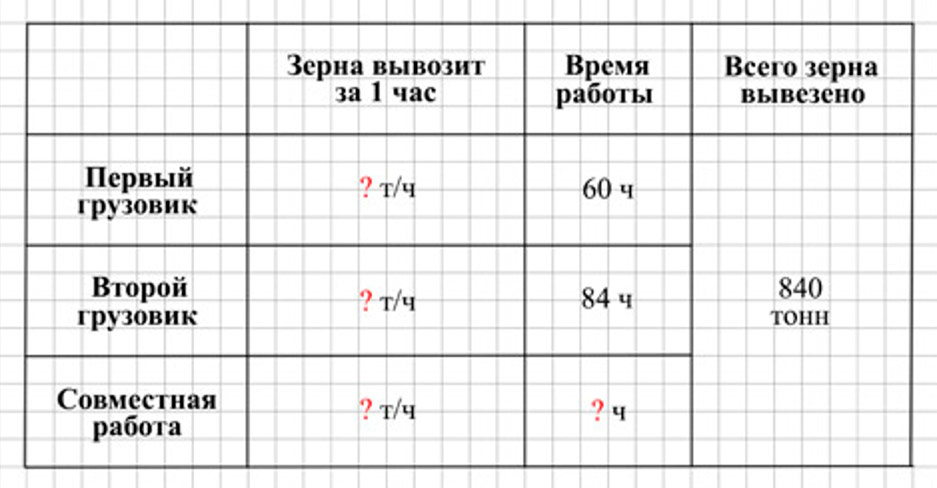
Рассуждаем.
Узнаем, сколько тонн зерна перевозит первый грузовик за 1 час.
1) 840 : 60 = 14 (т) – зерна перевозит первый грузовик за 1 час.
Продолжаем рассуждение.
Узнаем, сколько тонн зерна перевозит второй грузовик за 1 час.
2) 840 : 84 = 10 (т) – зерна перевозит второй грузовик за 1 час.
Продолжаем рассуждение.
Узнаем, сколько тонн зерна перевозят оба грузовика за 1 час.
3) 14 + 10 = 24 (т) – зерна перевозят оба грузовика за 1 час.
Продолжаем рассуждение.
Узнаем, сколько времени потребуется грузовикам при совместной работе, чтобы перевезти 840 тонн зерна.
4) 840 : 24 = 35 (ч) – потребуется грузовикам при совместной работе, чтобы перевезти 840 т зерна.
Записываем ответ.
Ответ: 35 часов.
Номер 24.
Между Москвой и Санкт-Петербургом расположен город Тверь. От Москвы до Твери по железной дороге 167 км. Это на 317 км меньше, чем от Твери до Санкт-Петербурга. Составь, используя эти данные, различные задачи и реши их.
Ответ:Задача 1: Между Москвой и Санкт-Петербургом расположен город Тверь. От Москвы до Твери по железной дороге 167 км. Это на 317 км меньше, чем от Твери до Санкт-Петербурга. Какое расстояние от Твери до Санкт-Петербурга по железной дороге?
.jpg "Изображение математика 4 класс Моро, Бантова - 2 часть страница 71, номер 24, задача 1")
167 + 317 = 484 (км) – расстояние от Твери до Санкт-Петербурга по железной дороге.
Ответ: расстояние от Твери до Санкт-Петербурга составляет 484 км.
Задача 2:
Между Москвой и Санкт-Петербургом расположен город Тверь. От Москвы до Твери по железной дороге 167 км. Это на 317 км меньше, чем от Твери до Санкт-Петербурга. Какое расстояние от Москвы до Санкт-Петербурга по железной дороге?
.jpg "Изображение математика 4 класс Моро, Бантова - 2 часть страница 71, номер 24, задача 2")
1) 167 + 317 = 484 (км) – расстояние от Твери до Санкт-Петербурга по железной дороге.
2) 167 + 484 = 651 (км) – расстояние от Москвы до Санкт-Петербурга по железной дороге.
Ответ: расстояние от Москвы до Санкт-Петербурга составляет 651 км.
Повтори единицу длины – километр.
Шаг 1.
Составляем условие первой задачи.
Между Москвой и Санкт-Петербургом расположен город Тверь. От Москвы до Твери по железной дороге 167 км. Это на 317 км меньше, чем от Твери до Санкт-Петербурга. Какое расстояние от Твери до Санкт-Петербурга по железной дороге?
Оформляем условие в виде краткой записи.
Рассуждаем.
Найдем расстояние от Твери до Санкт-Петербурга по железной дороге.
167 + 317 = 484 (км) – расстояние от Твери до Санкт-Петербурга по железной дороге.
Записываем ответ.
Ответ: 484 км.
Шаг 1.
Составляем условие второй задачи.
Между Москвой и Санкт-Петербургом расположен город Тверь. От Москвы до Твери по железной дороге 167 км. Это на 317 км меньше, чем от Твери до Санкт-Петербурга. Какое расстояние от Москвы до Санкт-Петербурга по железной дороге?
Оформляем условие в виде краткой записи.
Рассуждаем.
Найдем расстояние от Твери до Санкт-Петербурга по железной дороге.
1) 167 + 317 = 484 (км) – расстояние от Твери до Санкт-Петербурга по железной дороге.
Продолжаем рассуждение.
Найдем расстояние от Москвы до Санкт-Петербурга по железной дороге.
2) 167 + 484 = 651 (км) – расстояние от Москвы до Санкт-Петербурга по железной дороге.
Записываем ответ.
Ответ: 651 км.
Номер 25.
Денис хотел записать на кассету мультфильмы, показ которых длится 46 мин, 48 мин, 26 мин, 54 мин, 32 мин. Поместятся ли все они на 180-минутной кассете? Какие мультфильмы выгоднее записать, чтобы оставалось меньше свободного места?
Ответ:
1) 46 + 48 + 26 + 54 + 32 = 206 (мин) – продолжительность всех мультфильмов.
2) 206 мин > 180 мин.
Все мультфильмы на кассете не поместятся.
3) 206 - 180 = 26 мин - выгоднее записать все мультфильмы кроме 26-минутного.
Ответ: на кассету можно записать все фильмы, кроме 26-минутного мультфильма.
Повтори единицу времени – минуту.
Выполняем вычисления.
1) 46 + 48 + 26 + 54 + 32 = 206 (мин) – продолжительность всех мультфильмов.
2) 206 мин > 180 мин.
Все мультфильмы на кассете не поместятся.
3) 206 – 180 = 26 мин.
Ответ: на кассету можно записать все фильмы, кроме 26-минутного мультфильма.
Оформляем задание в тетрадь.
Номер 3.
Выбери высказывания, верные для данного рисунка.
1) Если фигура жёлтого цвета, то это не треугольник.
2) Все треугольники красного цвета.
3) Если фигура красного цвета, то это прямоугольный треугольник.
4) Фигура зелёного цвета − это равнобедренный треугольник.
1) Верно. 2) Неверно, так как также на рисунке есть треугольники зеленого и голубого цвета. 3) Неверно, так как на рисунке также есть тупоугольный треугольник красного цвета. 4) Верно.
Номер 4.
1) Вычислительная машина работает так: к введённому числу ☐ прибавляет 20 (☐ + 20); результат сравнивает с числом 100: (☐ + 20) < 100?:
если "НЕТ": (☐ + 20) > 100, машина подаёт результат на выход;
если "ДА": (☐ + 20) < 100, машина подаёт результат снова на вход и повторяет то, что выполняла раньше.
2) Какое число будет получаться на выходе из машины, если в неё ввели число: 78; 46; 35; 29; 89; 54?
Вход: 78
78 + 20 = 98
98 < 100 − ДА
98 + 20 = 118
118 < 100 − НЕТ
Выход: 118
Вход: 46
46 + 20 = 66
66 < 100 − ДА
66 + 20 = 86
86 < 100 − ДА
86 + 20 = 106
106 < 100 − НЕТ
Выход: 106
Вход: 35
35 + 20 = 55
55 < 100 − ДА
55 + 20 = 75
75 < 100 − ДА
75 + 20 = 95
95 < 100 − ДА
95 + 20 = 115
115 < 100 − НЕТ
Выход: 115
Вход: 29
29 < 100 − ДА
29 + 20 = 49
49 < 100 − ДА
49 + 20 = 69
69 < 100 − ДА
69 + 20 = 89
89 < 100 − ДА
89 + 20 = 109
109 < 100 − НЕТ
Выход: 109
Вход: 89
89 < 100 − ДА
89 + 20 = 109
109 < 100 − НЕТ
Выход: 109
Вход: 54
54 + 20 = 74
74 < 100 − ДА
74 + 20 = 94
94 < 100 − ДА
94 + 20 = 114
114 < 100 − НЕТ
Выход: 114
Номер 5.
Вычислительная машина работает так:
1) Составь план её работы.
2) Какие числа будут получаться на выходе из машины, если в неё ввели числа: 480; 360; 270; 890?
1) Вычислительная машина работает так:
к введенному число прибавляет 300 (☐ + 300);
результат сравнивает с числом 1000: (☐ + 300) < 1000?;
если “НЕТ”: (☐ + 300) > 1000, машина подает результат на выход;
если “ДА”: (☐ + 300) < 1000, машина подает результат снова на вход и повторяет то, что выполняла раньше.
2) Вход: 480
480 + 300 = 780
780 < 1000 − ДА
780 + 300 = 1080
1080 < 1000 − НЕТ
Выход: 1080
Вход: 360
360 + 300 = 660
660 < 1000 − ДА
660 + 300 = 960
960 < 1000 − ДА
960 + 300 = 1260
1260 < 1000 − НЕТ
Выход: 1260
Вход: 270
270 + 300 = 570
570 < 1000 − ДА
570 + 300 = 870
870 < 1000 − ДА
870 + 300 = 1170
1170 < 1000 − НЕТ
Выход: 1170
Вход: 890
890 + 300 = 1190
1190 < 1000 − НЕТ
Выход: 1190
Номер 6.
Капроновый шнур длиной 30 м разрезали на 3 части так, что одна часть на 1 м длиннее другой и на 1 м короче третьей. Найди длину каждой части. Совет: сделай схематический чертёж.
Ответ:
Метод подбора:
Нужно найти такую комбинацию чисел, которые в ряду стоят друг за другом, например, 1, 2, 3, но чтобы в сумме давали 30. Это числа 9, 10 и 11, значит длины кусков - 9 метров, 10 метров и 11 метров.
Ответ: 9 метров, 10 метров, 11 метров.
Метод вычислений:
1) 30 : 3 = 10 (м) - приходился бы на каждый кусок, если бы они были равны.
2) 10 − 1 = 9 (м) - длина первого куска.
3) 10 + 1 = 11 (м) - длина третьего куска.
Ответ: 9 метров, 10 метров и 11 метров.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽
Напишите свой комментарий.