Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 66
- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
.jpg "Математика 4 класс Моро, Волкова - 2 часть страница 66")
Номер 270.
1) Каждый час токарь изготавливал по 10 деталей и всего изготовил 70 деталей. Сколько часов он работал?
2) Один токарь каждый час изготавливает 8 деталей, а другой – 7 деталей. За сколько часов они изготовят вместе 90 деталей, если выработка в час у них не изменится?
Составь и реши задачи, обратные данной.
Задача 1:
Деталей за 1 ч - 10 шт.
Всего деталей - 70 шт.
Время работы - ? ч
70 : 10 = 7 (ч) – работал токарь.
Ответ: 7 часов всего работал токарь.
Обратная задача 1:
Токарь работал 7 ч и изготовил 70 деталей. Какова выработка в час у токаря?
Деталей за 1 ч - ? шт.
Всего деталей - 70 шт.
Время работы - 7 ч
70 : 7 = 10 (ед.) – в час делал токарь.
Ответ: выработка токаря 10 деталей в час.
Обратная задача 2:
Токарь работал 7 ч и изготавливал в час 10 деталей. Сколько всего деталей изготовил токарь?
Деталей за 1 ч - 10 шт.
Всего деталей - ? шт.
Время работы - 7 ч
10 ∙ 7 = 70 (дет.) – всего изготовил токарь.
Ответ: токарь изготовил 70 деталей.
Задача 2:
.jpg "Изображение математика 4 класс Моро, Бантова - 2 часть страница 66, номер 270, задача 2")
1) 8 + 7 = 15 (д.) – изготавливают оба токаря за 1 ч.
2) 90 : 15 = 6 (ч) – изготовят 90 деталей.
Ответ: за 6 ч изготовят 90 деталей.
Обратная задача:
Один токарь каждый час изготавливает 8 деталей, а другой – 7 деталей. Сколько деталей они изготовят вместе за 6 ч, если выработка в час у них не изменится.
.jpg "Изображение математика 4 класс Моро, Бантова - 2 часть страница 66, номер 270, обратная задача")
1) 8 + 7 = 15 (д.) – изготавливают оба токаря за 1 ч.
2) 15 ∙ 6 = 90 (д.) – изготовят за 6 ч.
Ответ: 90 деталей изготовят за 6 часов.
Повтори, что такое обратные задачи и единицу времени – час.
Шаг 1.
Оформляем условие в виде краткой записи.
Деталей за 1 ч – 10 шт.
Всего деталей – 70 шт.
Время работы – ? ч
Рассуждаем.
Узнаем, сколько часов работал токарь, для этого количество всех выполненных деталей разделим на количество деталей, которые токарь делал за час.
70 : 10 = 7 (ч) – работал токарь.
Записываем ответ.
Ответ: 7 часов.
Шаг 1.
Составляем задачу, обратную данной.
Токарь работал 7 ч и изготовил 70 деталей. Какова выработка в час у токаря?
Оформляем условие в виде краткой записи.
Деталей за 1 ч – ? шт.
Всего деталей – 70 шт.
Время работы – 7 ч
Рассуждаем.
Узнаем, сколько деталей изготавливает токарь в час.
70 : 7 = 10 (ед.) – в час делал токарь.
Записываем ответ.
Ответ: выработка токаря 10 деталей в час.
Шаг 1.
Оформляем условие в виде таблицы.
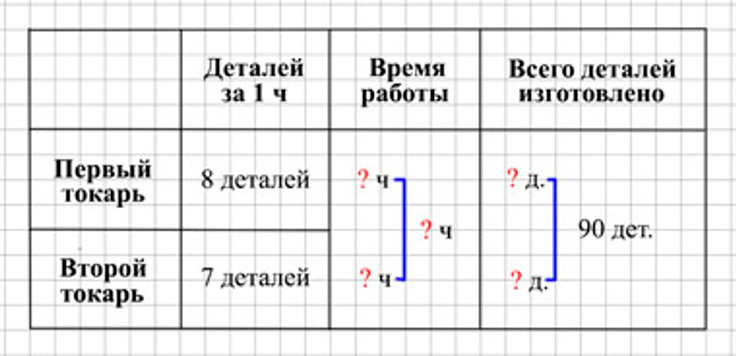
Рассуждаем.
Узнаем, сколько деталей изготавливают оба токаря за один час.
1) 8 + 7 = 15 (д.) – изготавливают оба токаря за 1 ч.
Продолжаем рассуждение.
Узнаем, за какое время изготовят 90 деталей.
2) 90 : 15 = 6 (ч) – изготовят 90 деталей.
Записываем ответ.
Ответ: за 6 ч изготовят 90 деталей.
Шаг 1.
Составляем задачу, обратную данной.
Один токарь каждый час изготавливает 8 деталей, а другой – 7 деталей. Сколько деталей они изготовят вместе за 6 ч, если выработка в час у них не изменится?
Оформляем условие в виде таблицы.
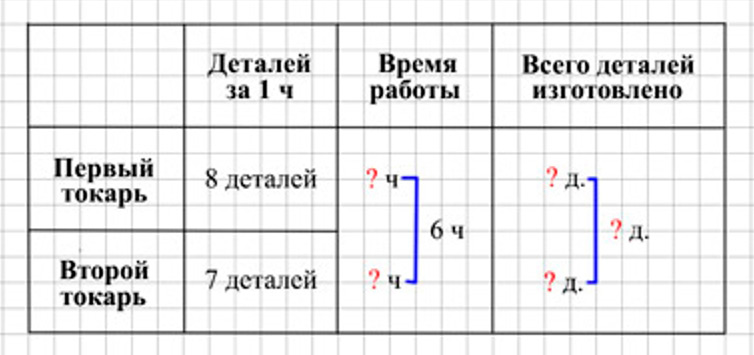
Рассуждаем.
Узнаем, сколько деталей изготавливают оба токаря за один час.
1) 8 + 7 = 15 (д.) – изготавливают оба токаря за 1 ч.
Продолжаем рассуждение.
Узнаем, сколько деталей изготовят на 6 часов.
2) 15 ∙ 6 = 90 (д.) – изготовят за 6 ч.
Записываем ответ.
Ответ: 90 деталей изготовят за 6 часов.
Номер 271.
Выполни деление с объяснением.
Ответ:
1) 192480 : 24 Для этого выделю первое неполное делимое – 192 (тысячи). Нахожу первую цифру частного: 192 : 24 = 8 (тысяч). Образую второе неполное делимое: 24 ∙ 8 = 192, 192 − 192 = 0.Добавляю оставшиеся 4 сотни – 4. Нахожу вторую цифру частного: 4 : 24 = 0 (сотен). Образую третье неполное делимое: добавляю к 4 сотням оставшиеся 8 десятков – 48. Нахожу третью цифру частного: 48 : 24 = 2 (десятка). Образую четвёртое неполное делимое: 24 ∙ 2 = 48, 48 − 48 = 0. Добавляю оставшиеся 0 единиц – 0. Нахожу четвёртую цифру частного: 0 : 24 = 0. Проверка:
.jpg "Изображение математика 4 класс Моро, Бантова - 2 часть страница 66, номер 271, пример 1")
Читаю ответ: при делении 192480 на 24 получится 8020.
2) 146880 : 36
Для этого выделю первое неполное делимое – 146 (тысяч).
Нахожу первую цифру частного: 146 : 36 = 4 (тысячи).
Образую второе неполное делимое: 36 ∙ 4 = 144, 146 − 144 = 2.Добавляю оставшиеся 8 сотен – 28.
Нахожу вторую цифру частного: 28 : 36 = 0 (сотен).
Образую третье неполное делимое: добавляю к 28 сотням оставшиеся 8 десятков – 288.
Нахожу третью цифру частного: 288 : 36 = 8 (десятков).
Образую четвёртое неполное делимое: 36 ∙ 8 = 288, 288 ∙ 288 = 0.
Добавляю оставшиеся 0 единиц – 0.
Нахожу четвёртую цифру частного: 0 : 36 = 0.
Проверка:
.jpg "Изображение математика 4 класс Моро, Бантова - 2 часть страница 66, номер 271, пример 2")
Читаю ответ: при делении 146880 на 36 получается 4080.
3) 143520 : 16
Разделю 143520 на 16. Для этого выделю первое неполное делимое – 143 (тысячи).
Нахожу первую цифру частного: 143 : 16 = 8 (тысяч).
Образую второе неполное делимое: 16 ∙ 8 = 128, 143 − 128 = 15. Добавляю оставшиеся 5 сотен – 155.
Нахожу вторую цифру частного: 155 : 16 = 9 (сотен).
Образую третье неполное делимое: 16 ∙ 9 = 144, 155 − 144 = 11. Добавляю оставшиеся 2 десятка – 112.
Нахожу третью цифру частного: 112 : 16 = 7 (десятков).
Образую четвёртое неполное делимое: 16 ∙ 7 = 112, 112 − 112 = 0.
Добавляю оставшиеся 0 единиц – 0.
Нахожу четвёртую цифру частного: 0 : 16 = 0.
Проверка:
.jpg "Изображение математика 4 класс Моро, Бантова - 2 часть страница 66, номер 271, пример 3")
Читаю ответ:при делении 143520 на 16 получается 8970.
Повтори алгоритм письменного деления на двузначные числа.
Выполняем вычисления с объяснением.
1) 192480 : 24
Для этого выделю первое неполное делимое – 192 (тысячи).
Нахожу первую цифру частного: 192 : 24 = 8 (тысяч).
Образую второе неполное делимое: 24 ∙ 8 = 192, 192 − 192 = 0.
Добавляю оставшиеся 4 сотни – 4.
Нахожу вторую цифру частного: 4 : 24 = 0 (сотен).
Образую третье неполное делимое: добавляю к 4 сотням оставшиеся 8 десятков – 48.
Нахожу третью цифру частного: 48 : 24 = 2 (десятка).
Образую четвёртое неполное делимое: 24 ∙ 2 = 48, 48 − 48 = 0.
Добавляю оставшиеся 0 единиц – 0.
Нахожу четвёртую цифру частного: 0 : 24 = 0.
Проверка:
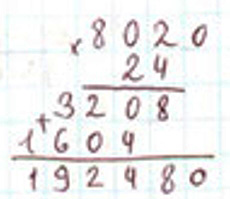
Читаю ответ: при делении 192480 на 24 получится 8020.
2) 146880 : 36
Для этого выделю первое неполное делимое – 146 (тысяч).
Нахожу первую цифру частного: 146 : 36 = 4 (тысячи).
Образую второе неполное делимое: 36 ∙ 4 = 144, 146 − 144 = 2.
Добавляю оставшиеся 8 сотен – 28.
Нахожу вторую цифру частного: 28 : 36 = 0 (сотен).
Образую третье неполное делимое: добавляю к 28 сотням оставшиеся 8 десятков – 288.
Нахожу третью цифру частного: 288 : 36 = 8 (десятков).
Образую четвёртое неполное делимое: 36 ∙ 8 = 288, 288 ∙ 288 = 0.
Добавляю оставшиеся 0 единиц – 0.
Нахожу четвёртую цифру частного: 0 : 36 = 0.
Проверка:
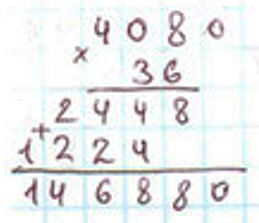
Читаю ответ: при делении 146880 на 36 получается 4080.
3) 143520 : 16
Разделю 143520 на 16. Для этого выделю первое неполное делимое – 143 (тысячи).
Нахожу первую цифру частного: 143 : 16 = 8 (тысяч).
Образую второе неполное делимое: 16 ∙ 8 = 128, 143 − 128 = 15.
Добавляю оставшиеся 5 сотен – 155.
Нахожу вторую цифру частного: 155 : 16 = 9 (сотен).
Образую третье неполное делимое: 16 ∙ 9 = 144, 155 − 144 = 11.
Добавляю оставшиеся 2 десятка – 112.
Нахожу третью цифру частного: 112 : 16 = 7 (десятков).
Образую четвёртое неполное делимое: 16 ∙ 7 = 112, 112 − 112 = 0.
Добавляю оставшиеся 0 единиц – 0.
Нахожу четвёртую цифру частного: 0 : 16 = 0.
Проверка:
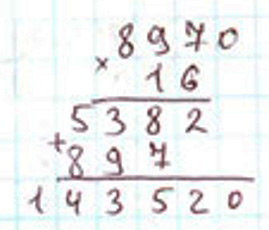
Читаю ответ: при делении 143520 на 16 получается 8970.
Оформляем задание в тетрадь.
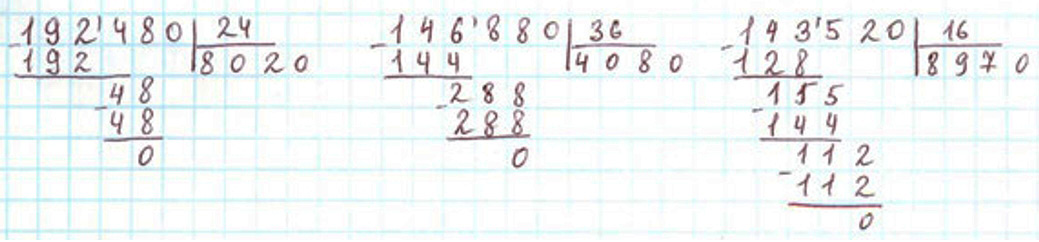
Номер 272.
Ответ:
Повтори алгоритм письменного вычитания, умножения и деления многозначных чисел, а также порядок действий.
Выполняем вычисления с пояснениями.
Пишу: 273 150 : 45.
Разделю 273 150 на 45. Выделю первое неполное делимое – 273. Разделю 27 на 4, получу 6 – это пробная цифра.
Проверяю, подходит ли цифра 6.
Умножу 45 на 6, получу 270.
273 – 270 = 3. Добавляю 1 сот.
Нахожу вторую цифру частного: 31 : 45.
31 меньше, чем 45, пишу в частном 0. Добавляю 5 дес.
Нахожу третью цифру частного:
315 : 45, получу 7. 315 – 315 = 0.
Нахожу четвёртую цифру частного:
0 : 45 = 0.
Частное – 6070.
Пишу: 449 920 : 64.
Разделю 449 920 на 64. Выделю первое неполное делимое – 449. Разделю 44 на 6, получу 7 – это пробная цифра.
Проверяю, подходит ли цифра 7.
Умножу 64 на 7, получу 448.
449 – 448 = 1. Добавляю 9 сот.
Нахожу вторую цифру частного: 19 : 64.
19 меньше, чем 64, пишу в частном 0. Добавляю 2 дес.
Нахожу третью цифру частного:
192 : 64, получу 3. 192 – 192 = 0.
Нахожу четвёртую цифру частного:
0 : 64 = 0.
Частное – 7030.
Пишу: 479 120 : 53.
Разделю 479 120 на 53. Выделю первое неполное делимое – 479. Разделю 47 на 5, получу 9 – это пробная цифра.
Проверяю, подходит ли цифра 9.
Умножу 53 на 9, получу 477.
479 – 477 = 2. Добавляю 1 сот.
Нахожу вторую цифру частного: 21 : 53.
21 меньше, чем 53, пишу в частном 0. Добавляю 2 дес.
Нахожу третью цифру частного:
212 : 53, получу 4. 212 – 212 = 0.
Нахожу четвёртую цифру частного:
0 : 53 = 0.
Частное – 9 040.
Пишу: 923 400 : 19.
Разделю 923 400 на 19. Выделю первое неполное делимое – 92. Разделю 92 на 19, получу 4.
92 – 76 = 16. Добавляю 3 тыс.
Нахожу вторую цифру частного:
163 : 19, получу 8.
Умножу 19 на 8, получу 152.
163 – 152 = 11. Добавляю 4 сот.
Нахожу третью цифру частного:
114 : 19, получу 6.
Умножу 19 на 6, получу 114.
114 – 114 = 0.
Нахожу четвёртую цифру частного:
0 : 19 = 0.
Нахожу четвёртую цифру частного:
0 : 19 = 0.
Частное – 48 600.
Пишу: 676 800 : 18.
Разделю 676 800 на 18. Выделю первое неполное делимое – 67. Разделю 67 на 18, получу 3.
67 – 54 = 13. Добавляю 6 тыс.
Нахожу вторую цифру частного:
136 : 18, получу 7.
Умножу 18 на 7, получу 126.
136 – 126 = 10. Добавляю 8 сот.
Нахожу третью цифру частного:
108 : 18, получу 6.
Умножу 18 на 6, получу 108.
108 – 108 = 0.
Нахожу четвёртую цифру частного:
0 : 18 = 0.
Нахожу четвёртую цифру частного:
0 : 18 = 0.
Частное – 37 600.
Пишу: 899 200 : 16.
Разделю 899 200 на 16. Выделю первое неполное делимое – 89. Разделю 89 на 16, получу 5. 89 – 80 = 9. Добавляю 9 тыс.
Нахожу вторую цифру частного:
99 : 16, получу 6.
Умножу 16 на 6, получу 96.
99 – 96 = 3. Добавляю 2 сот.
Нахожу третью цифру частного:
32 : 16, получу 2.
Умножу 16 на 2, получу 32.
32 – 32 = 0.
Нахожу четвёртую цифру частного:
0 : 16 = 0.
Нахожу четвёртую цифру частного:
0 : 16 = 0.
Частное – 56 200.
Оформляем задание в тетрадь.
Номер 273.
Для перевозки молока созданы специальные машины – молоковозы-гиганты. В прошлом году город обслуживали 5 таких машин, а в этом году – 7. На семи машинах стали привозить на 38 т молока больше, чем раньше. Сколько тонн молока привозили в город на молоковозах-гигантах в прошлом году и сколько в этом?
Ответ:
1) 7 − 5 = 2 (м) – на столько больше стало машин в этом году, чем в прошлом.
2) 38 : 2 = 19 (т) – молока перевозит одна машина.
3) 19 ∙ 5 = 95 (т) – молока привозили в прошлом году.
4) 19 ∙ 7 = 133 (т) – молока привозили в этом году.
Ответ: 95 т молока всего привезли в прошлом году, 133 т молока привозили в этом году.
Повтори единицу массы – тонну.
Оформляем условие в виде таблицы.
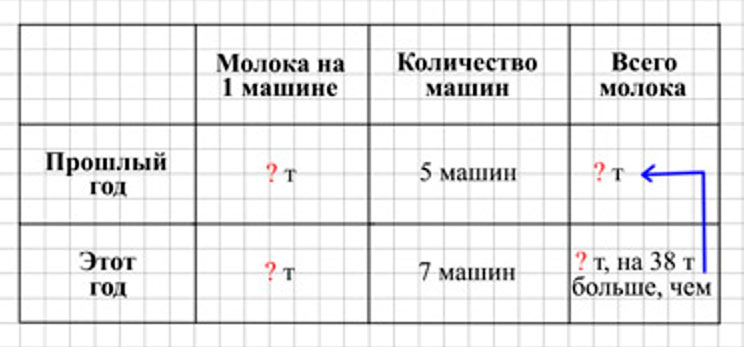
Рассуждаем.
Узнаем, на сколько больше стало машин в этом году, чем в прошлом.
1) 7 − 5 = 2 (м) – на столько больше стало машин в этом году, чем в прошлом.
Продолжаем рассуждение.
Узнаем, сколько молока перевозит одна машина.
2) 38 : 2 = 19 (т) – молока перевозит одна машина.
Продолжаем рассуждение.
Узнаем, сколько молока привозили в город в прошлом году.
3) 19 ∙ 5 = 95 (т) – молока привозили в прошлом году.
Продолжаем рассуждение.
Узнаем, сколько молока привозили в город в этом году.
4) 19 ∙ 7 = 133 (т) – молока привозили в этом году.
Записываем ответ.
Ответ: 95 т, 133 т.
Номер 274.
На автомашине с прицепом нужно перевезти 1080 ц угля. За один рейс на машине увозили 30 ц, а на прицепе – в 2 раза меньше. Сколько рейсов надо сделать, чтобы перевезти весь уголь?
Ответ:
1) 30 : 2 = 15 (ц) – масса угля на прицепе.
2) 30 + 15 = 45 (ц) – масса угля на машине с прицепом.
3) 1080 : 45 = 24 (р.) – нужно сделать.
Ответ: 24 рейса всего нужно сделать, чтобы перевезти весь уголь.
Повтори единицу массы – центнер, а также алгоритм деления на двузначные числа.
Оформляем условие в виде таблицы.
Рассуждаем.
Узнаем, сколько центнеров угля можно перевезти на прицепе за один раз.
1) 30 : 2 = 15 (ц) – масса угля на прицепе.
Продолжаем рассуждение.
Узнаем, сколько центнеров угля можно перевезти на машине с прицепом за раз.
2) 30 + 15 = 45 (ц) – масса угля на машине с прицепом.
Продолжаем рассуждение.
Вычислим, сколько рейсов нужно сделать, чтобы перевезти весь уголь.
3) 1080 : 45 = 24 (р.)
Записываем ответ.
Ответ: 24 рейса нужно сделать.
Номер 275.
Запиши неравенства и докажи, что они верны.
1) Произведение чисел 3806 и 1 меньше их суммы.
2) Произведение чисел 17489 и 0 меньше их суммы.
1) 3806 ∙ 1 < 3806 + 1
3806 < 3807 – верно, так как когда мы умножаем число на 1, мы получаем число равное данному, а когда прибавляем 1 - получаем число, больше данного на 1.
2) 17489 ∙ 0 < 17489 + 0
0 < 17489 – верно, так как когда мы умножаем число на 0, мы получаем ноль, а когда прибавляем 0 - получаем число, равное данному.
Повтори, как называются числа при сложении и умножении, а также что такое неравенства.
Запишем первое неравенство и докажем, что оно верное.
3806 ∙ 1 < 3806 + 1
3806 < 3807 – верно, так как когда мы умножаем число на 1, мы получаем число равное данному, а когда прибавляем 1 – получаем число, больше данного на 1.
Запишем второе неравенство и докажем, что оно верное
17489 ∙ 0 < 17489 + 0
0 < 17489 – верно, так как когда мы умножаем число на 0, мы получаем нуль, а когда прибавляем 0 – получаем число, равное данному.
Номер 276.
1) Найди делимое, если делитель 34, частное 8050, а остаток 12. Проверь, выполнив деление.
2) Найди делимое, если делитель 17, частное 124, а остаток 2. Сделай проверку.
Повтори алгоритм письменного умножения и деления на двузначные числа.
Выполняем вычисления с пояснением.
Чтобы найти делимое, нужно частное умножить на делить и прибавить остаток.
Оформляем задание в тетрадь.
Номер 277.
Какое наибольшее число квадратов со стороной 2 см можно вырезать из квадрата, площадь которого равна 1 дм²?
Ответ:
Площадь маленького квадрата = 2 см ∙ 2 см = 4 см²
1 дм² = 100 см²
100 : 4 = 25 (кв.) – можно вырезать из квадрата, площадь которого равна 1 дм2.
Ответ: 25 квадратов всего можно вырезать из квадрата.
Повтори, как найти площадь многоугольника.
Рассуждаем и выполняем вычисления.
Площадь маленького квадрата = 2 см ∙ 2 см = 4 см²
1 дм² = 100 см²
100 : 4 = 25 (кв.) – можно вырезать из квадрата, площадь которого равна 1 дм².
Ответ: 25 квадратов.
Оформляем задание в тетрадь.
Номер 278.
Чтобы открыть сейф, нужно знать код. Известно, что код – трёхзначное число, записанное тремя разными цифрами из цифр 1, 2, 3, 4, и это число больше, чем 400. Сколько чисел нужно проверить, чтобы узнать код?
Ответ:По условию известно, что кодовое число больше 400, значит первая цифра в нем 4. Остается проверить 3 цифры и комбинации из них. Получатся 6 вариантов: 12, 21, 13, 31, 23, 32, соответственно, нужно проверить 6 чисел: 412, 413, 421, 423, 431, 432.
Повтори состав трёхзначных чисел.
Рассуждаем.
По условию известно, что кодовое число больше 400, значит первая цифра в нем 4. Остается проверить 3 цифры и комбинации из них.
Получатся 6 вариантов: 12, 21, 13, 31, 23, 32, соответственно, нужно проверить 6 чисел:
412, 413, 421, 423, 431, 432.
Оформляем задание в тетрадь.
6 чисел.
Задание на полях страницы
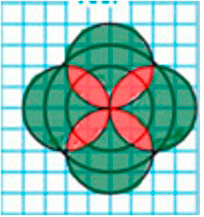
Начерти и раскрась узор.
Ответ:
Повтори, что такое окружность.
Рассуждаем.
1) Начерти окружность с радиусом 1 см.
2) Начерти 4 такие же окружности так, чтобы они пересеклись в том же центре.
3) Из того же центра проведи окружность с радиусом 1 см 5 мм.
4) Раскрась.
Оформляем задание в тетрадь.
Задание внизу страницы
Номер 271.
Ответ:
Номер 272.
Реши задачи и сравни их решения.
1) Длина водохранилища 600 км, а его ширина 400 км. Поездка на катере через водохранилище по его длине занимает на 10 ч больше, чем по ширине. За сколько времени при одинаковой скорости можно пересечь водохранилище по его длине и по ширине?
2) Длина водохранилища на 200 км больше его ширины. Поездка на катере с одинаковой скоростью через водохранилище по его длине занимает 30 ч, а по ширине – 20 ч. Найди длину и ширину этого водохранилища.
Задача 1:
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 66, номер 272, задача 1, 2024 год.")
1) 600 − 400 = 200 (км) – расстояние, которое проходит катер за 10 ч.
2) 200 : 10 = 20 (км/ч) – скорость катера.
3) 600 : 20 = 30 (ч) – время поездки по длине водохранилища.
4) 400 : 20 = 20 (ч) – время поездки по ширине водохранилища.
Ответ: время поездки по длине водохранилища составляет 30 ч и время движения по ширине водохранилища составляет 20 ч.
Задача 2:
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 66, номер 272, задача 2, 2024 год.")
1) 30 − 20 = 10 (ч) – время, за которое катер проходит расстояние в 200 км.
2) 200 : 10 = 20 (км/ч) – скорость катера.
3) 20 ∙ 30 = 600 (км) – длина водохранилища.
4) 20 ∙ 20 = 400 (км) – ширина водохранилища.
Ответ: длина водохранилища составляет 600 км и ширина водохранилища составляет 400 км.
Сравнение задач и их решений.
Эти задачи обратные. Рассмотрим решения задач. И в первой и во второй задаче сначала мы находили скорость катера, но в первой для этого мы искали неизвестное расстояние, которое проходят за 10 часов, а во второй – время, необходимое для прохождения расстояния в 200 км.
Затем искали нужное значение по вопросу задачи: в первой - время поездок по длине и ширине катера искали через деление: расстояние делили на найденную скорость, а во второй – длину и ширину водохранилища искали через умножение данных временных величин и найденной скорости.
Номер 273.
В питомнике вырастили саженцы деревьев: елей было 360, а на каждый 8 елей приходилось 18 клёнов и 16 лип. Сколько всего елей, клёнов и лип вырастили в питомнике?
Ответ:
1) 360 : 8 = 45 (р.) – по 8 елей содержится в питомнике.
2) 18 ∙ 45 = 810 (шт.) – клёнов.
3) 45 ∙ 16 = 720 (шт.) – лип.
4) 360 + 810 + 720 = 1890 (шт.) – деревьев, в питомнике.
Ответ: 1890 деревьев всего вырастили в питомнике.
Номер 274.
Ответ:
2 ц 50 кг ∙ 4 = 250 ц ∙ 4 = 1000 кг = 10 ц = 1 т
125 м ∙ 8 = 1000 м = 1 км
1 м 20 см ∙ 6 = 120 см ∙ 6 = 720 см = 7 м 20 см
1 м 20 см : 6 = 120 см : 6 = 20 см
2 мин 30 с ∙ 5 = 150 с ∙ 5 = 750 с = 12 мин 30 с
2 ч 30 мин : 5 = 150 мин : 5 = 30 мин
Номер 275.
Запиши неравенства и объясни, почему они верны.
1) Сумма чисел 289 и 1 больше их произведения.
2) Сумма чисел 289 и 0 больше их произведения.
3) Частное чисел 289 и 1 больше их разности.
1) 289 + 1 > 289 ∙ 1 − неравенство верно, так как когда мы прибавляем к числу 1, мы получаем число, большее на 1, а когда умножаем на 1, получаем число равное данному. 2) 289 + 0 > 289 ∙ 0 − неравенство верно, так как когда мы прибавляем к числу 0, мы получаем число, равное данному, а когда умножаем на 0, получаем 0. 3) 289 : 1 > 289 − 1 − неравенство верно, так как когда мы делим число на 1, то получаем число, равное данному, а когда вычитаем 1,получаем число, меньше данного на 1.
Номер 276.
Реши те уравнения, в которых неизвестное находят умножением.
Ответ:
х : 100 = 90
х - неизвестное делимое.
Чтобы найти неизвестное делимое, нужно делитель умножить на частное.
Решается умножением.
Подходит.
х = 100 ∙ 90
х = 9000
1200 : х = 60
х - неизвестный делитель.
Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
Решается делением.
Не подходит.
30 ∙ х = 1800
х - неизвестный множитель.
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
Решается делением.
Не подходит.
х : 18 = 30
х - неизвестное делимое.
Чтобы найти неизвестное делимое, нужно делитель умножить на частное.
Решается умножением.
Подходит.
х = 30 ∙ 18
х = 540
Номер 277.
Докажи, что в каждой окружности все диаметры делятся центром окружности на 2 равных отрезка.
Диаметр – отрезок проходящий через центр окружности и ограниченный двумя точками окружности. Этим центром окружности диаметр делится на два равных радиуса. Все радиусы окружности равны, а значит все диаметры делятся центром окружности на 2 равных отрезка. Зелёные отрезки ОА, ОС, ОВ, OD равны по длине как радиусы одной окружности. Красные отрезки ОК, ОМ, ОР, ОL также равны как радиусы одной окружности.
Номер 278.
Ответ:
Номер 279.
Школьная хоккейная площадка длиной 50 м и шириной 20 м обнесена бортиком прямоугольной формы высотой 1 м. Сколько краски потребуется для окраски бортика с внешней и внутренней сторон, если расход краски на 1 м² составляет 140 г и краска должна быть нанесена в 2 слоя?
Ответ:
1) 50 ∙ 1 = 50 (м²) – площадь длинного бортика хоккейной площадки.
2) 20 ∙ 1 = 20 (м²) – площадь короткого бортика хоккейной площадки.
3) (50 + 20) ∙ 2 = 140 (м²) – площадь всех бортиков с одной стороны.
4) 140 ∙ 2 = 280 (м²) – площадь всех бортиков с двух сторон.
5) 280 ∙ 140 = 39200 (г) – расход краски, нужно для покраски бортиков в 1 слой.
6) 39200 ∙ 2 = 78400 (г) – краски нужно для покраски всех бортиков с двух сторон.
Ответ: 78400 грамм краски или 78 кг 400 грамм нужно для покраски всех бортиков с двух сторон.
Задание внизу страницы
Вычисли.
Ответ:
Задание на полях страницы
Ребус.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽
Напишите свой комментарий.