Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 65
- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Задание вверху страницы
1) Объясни, как выполнено деление.
2) Рассмотри более короткую запись тех же вычислений.
1) Первая строка из 3 примеров: деление в них выполнено так, что при нахождении второго неполного частного получается нуль и из-за этого выполняется лишнее действие.
2) Во второй строке пропускается действие нахождения второго неполного частного, а вместо этого сразу сносится два знака к остатку при первом неполном частном и в частное записывается сразу нуль, а затем число единиц.
Повтори алгоритм письменного деления на двузначные числа.
Рассмотрим данные примеры.
Объясним, как выполнено деление.
1) Первая строка из 3 примеров: деление в них выполнено так, что при нахождении второго неполного частного получается нуль и из–за этого выполняется лишнее действие.
2) Во второй строке пропускается действие нахождения второго неполного частного, а вместо этого сразу сносится два знака к остатку при первом неполном частном и в частное записывается сразу нуль, а затем число единиц.
Номер 265.
Ответ:
Повтори алгоритм письменного деления на двузначные числа.
Выполняем вычисления с пояснениями.
Пишу: 13 915 : 23.
Разделю 13 915 на 23. Выделю первое неполное делимое – 139. Разделю 13 на 2, получу 6 – это пробная цифра.
Проверяю, подходит ли цифра 6.
Умножу 23 на 6, получу 138.
Образую второе неполное частное.
139 – 138 = 1 сот. Добавляю 1 дес., получаю 11.
Нахожу вторую цифру частного: 11 : 23. 11 меньше, чем 23, пишу в частном 0.
К 11 дес. добавляю 5 ед. получаю 115.
Нахожу третью цифру частного:
115 : 23 = 5.
Частное – 605.
Пишу: 17 238 : 34.
Разделю 17 238 на 34. Выделю первое неполное делимое – 172. Разделю 172 на 3, получу 5 – это пробная цифра.
Проверяю, подходит ли цифра 5.
Умножу 34 на 5, получу 170.
Образую второе неполное частное.
172 – 170 = 2 сот. Добавляю 3 дес., получаю 23.
Нахожу вторую цифру частного: 23 : 34. 23 меньше, чем 34, пишу в частном 0.
К 23 дес. добавляю 8 ед., получаю 238.
Нахожу третью цифру частного:
238 : 34 = 7.
Частное – 507.
Пишу: 3 696 : 12.
Разделю 36 на 12, получу 3.
Умножу 12 на 3, получу 36. 36 – 36 = 0.
Нахожу вторую цифру частного: 9 : 12. 9 меньше, чем 12, пишу в частном 0.
Нахожу третью цифру частного:
96 : 12 = 7.
Частное – 308.
Пишу: 7 605 : 15.
Разделю 76 на 15, получу 5.
Умножу 15 на 5, получу 75.
Образую второе неполное частное.
76 – 75 = 1 сот. Добавляю 0 дес., получаю 10.
Нахожу вторую цифру частного: 10 : 15. 10 меньше, чем 15, пишу в частном 0.
Нахожу третью цифру частного:
105 : 15 = 7.
Частное – 507.
Пишу: 26 880 : 32.
Разделю 26 880 на 32. Выделю первое неполное делимое – 268. Разделю 26 на 3, получу 8 – это пробная цифра.
Проверяю, подходит ли цифра 8.
Умножу 32 на 8, получу 256.
Образую второе неполное частное.
268 – 256 = 12 сот. Добавляю 8 дес., получаю 128.
Нахожу вторую цифру частного:
128 : 32. Разделю 12 на 3, получу 4 – это пробная цифра.
Проверяю, подходит ли цифра 4.
Умножу 32 на 4, получу 128.
128 – 128 = 0.
Нахожу третью цифру частного:
0 : 32 = 0.
Частное – 840.
Пишу: 36 540 : 87.
Разделю 36 540 на 87. Выделю первое неполное делимое – 365. Разделю 365 на 8, получу 4 – это пробная цифра.
Проверяю, подходит ли цифра 4.
Умножу 87 на 4, получу 348.
Образую второе неполное частное.
365 – 348 = 17 сот. Добавляю 4 дес.
Нахожу вторую цифру частного:
174 : 87. Разделю 17 на 8, получу 2 – это пробная цифра.
Проверяю, подходит ли цифра 2.
Умножу 87 на 2, получу 174.
174 – 174 = 0.
Нахожу третью цифру частного:
0 : 87 = 0.
Частное – 420.
Пишу: 319 ∙ 706.
Умножу первый множитель на число единиц:
319 ∙ 6 = 1 914.
Получу первое неполное произведение: 1 914.
В десятках второго множителя – ноль, поэтому пропускаем этап умножения на десятки.
Умножу первый множитель на число сотен:
319 ∙ 7 = 2 233.
Получу второе неполное произведение: 2 233 сот.
Начну подписывать второе неполное произведение под сотнями.
Сложу неполные произведения.
Читаю ответ: 225 214. Это произведение чисел 319 и 706.
Пишу: 405 ∙ 82.
Умножу первый множитель на число единиц:
405 ∙ 2 = 810.
Получу первое неполное произведение: 810.
Умножу первый множитель на число десятков:
405 ∙ 8 = 3 240.
Получу второе неполное произведение: 3 240 дес.
Начну подписывать второе неполное произведение под десятками.
Сложу неполные произведения.
Читаю ответ: 33 210. Это произведение чисел 405 и 82.
Выполняем проверку.
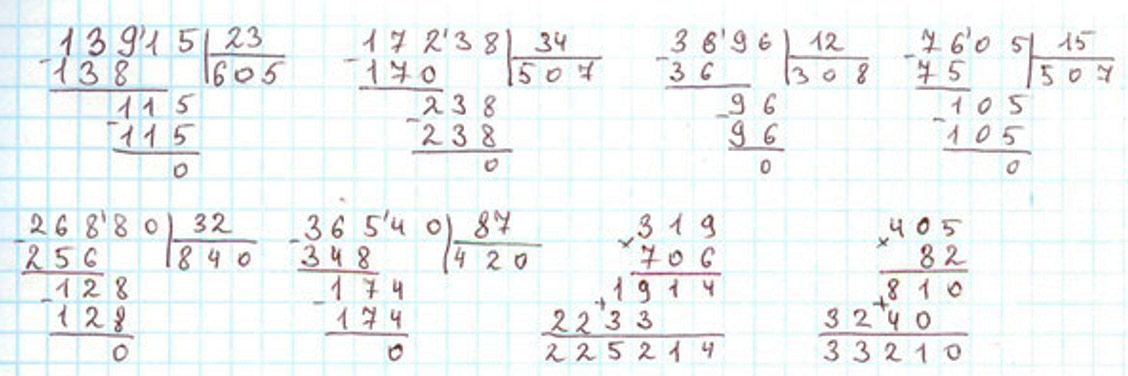
Номер 266.
И двух посёлков, находящихся на расстоянии 20 км, вышли одновременно навстречу друг другу два лыжника. Они встретились через 40 мин. Один из них шёл со скоростью 240 м/мин. Объясни, что показывают выражения.
Ответ:
20 км = 20000 м
1) 20000 : 40 – скорость сближения лыжников.
2) 20000 : 40 - 240 – скорость второго лыжника.
3) 240 ∙ 40 – расстояние, которое прошёл первый лыжник.
4) 20000 − 240 ∙ 40 – расстояние, которое прошёл второй лыжник.
Повтори взаимосвязь между скоростью, временем и расстоянием.
Оформляем условие в виде схематического чертежа.
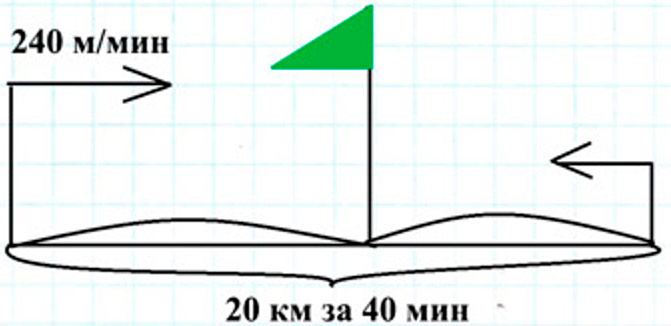
Объясним, что показывают данные выражения.
20 км = 20000 м
1) 20000 : 40 – скорость сближения лыжников.
2) 20000 : 40 – 240 – скорость второго лыжника.
3) 240 ∙ 40 – расстояние, которое прошёл первый лыжник.
4) 20000 − 240 ∙ 40 – расстояние, которое прошёл второй лыжник.
Номер 267.
Для посева заготовили семена ячменя, овса, проса – всего 220 т 5 ц. Ячменя было заготовлено 85 т, что на 9 т 5 ц больше, чем овса. Сколько проса заготовлено для посева?
Ответ:
1) 85 т − 9 т 5 ц = 850 ц − 95 ц = 755 ц = 75 т 5 ц – масса заготовленного овса.
2) 85 т + 75 т 5 ц = 850 ц + 755 ц = 1605 ц = 160 т 5 ц – масса ячменя и овса.
3) 220 т 5 ц − 160 т 5 ц = 2205 ц − 1605 ц = 600 ц = 60 т – масса проса.
Ответ: 60 тонн проса всего заготовлено для посева.
Повтори единицы массы – тонну и килограмм.
Оформляем условие в виде краткой записи.
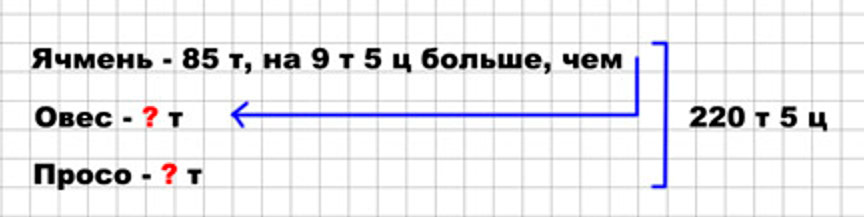
Рассуждаем.
Узнаем, массу заготовленного овса.
1) 85 т − 9 т 5 ц = 850 ц − 95 ц = 75 ц = 75 т 5 ц – масса заготовленного овса.
Продолжаем рассуждение.
Узнаем, массу ячменя и овса вместе.
2) 85 т + 75 т 5 ц = 850 ц + 755 ц = 1605 ц = 160 т 5 ц – масса ячменя и овса.
Продолжаем рассуждение.
Найдем массу проса.
3) 220 т 5 ц − 160 т 5 ц = 2205 ц − 1605 ц = 600 ц = 60 т – масса проса.
Записываем ответ.
Ответ: 60 тонн проса.
Номер 268.
Составь уравнения и реши их.
1) Какое число надо умножить на 42, чтобы получить разность чисел 500 и 38?
2) Какое число надо увеличить в 3 раза, чтобы получить число, равное сумме чисел 135 и 450?
1)
.jpg "Изображение математика 4 класс Моро, Бантова - 2 часть страница 65, номер 268, пример 1")
2)
.jpg "Изображение математика 4 класс Моро, Бантова - 2 часть страница 65, номер 268, пример 2")
Повтори, как решать уравнения.
Выполняем вычисления.
х ∙ 42 = 500 – 38
х ∙ 42 = 462
х = 462 : 42
х = 11
Проверка:
11 ∙ 42 = 500 – 38
462 = 462
Ответ: х = 11
х ∙ 3 = 135 + 450
х ∙ 3 = 585
х = 585 : 3
х = 195
Проверка:
195 ∙ 3 = 135 + 450
585 = 585
Ответ: х = 195
Оформляем задание в тетрадь.
1)
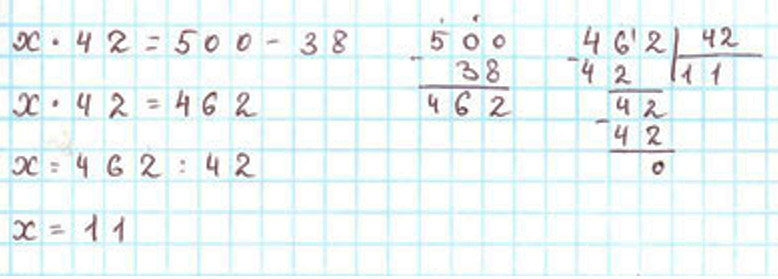
2)
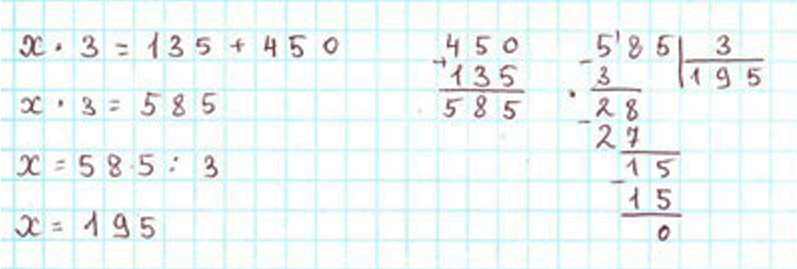
Номер 269.
Реши уравнения.
Ответ:
х ∙ 100 = 4500
х = 4500 : 100
х = 45
Проверка:
45 * 100 = 4500
4500 = 4500
Ответ: х = 45
у : 100 = 4500
у = 4500 ∙ 100
у = 450000
Проверка:
450000 : 100 = 4500
4500 = 4500
Ответ: у = 450000
Повтори, как решать уравнения.
Выполняем вычисления с пояснением.
1. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель:
4 500 : 100 = 45.
Проверка:
45 ∙ 100 = 4 500
4 500 = 4 500
2. Чтобы найти делимое, нужно частное умножить на делитель:
4 500 ∙ 100 = 450 000.
Проверка:
450 000 : 100 = 4 500
4 500 = 4 500
Оформляем задание в тетрадь.
х ∙ 100 = 4 500
х = 4 500 : 100
х = 45
Проверка:
45 ∙ 100 = 4 500
4 500 = 4 500
Ответ: х = 45
у : 100 = 4 500
у = 4 500 ∙ 100
у = 450 000
Проверка:
450 000 : 100 = 4 500
4 500 = 4 500
Ответ: у = 450 000
Задание внизу страницы
Сколько минут в одной двенадцатой части часа? в одной пятнадцатой части часа?
Ответ:1 час = 60 мин 60 : 12 ∙ 1 = 5 мин – в одной двенадцатой части часа. 60 : 15 ∙ 1 = 4 мин – в одной пятнадцатой части часа.
Повтори, что такое доли.
Выполняем вычисления.
1 час = 60 мин
60 : 12 ∙ 1 = 5 мин – в одной двенадцатой части часа.
60 : 15 ∙ 1 = 4 мин – в одной пятнадцатой части часа.
Оформляем задание в тетрадь.
Задание на полях страницы
Продолжи и вычисли.
Ответ:
1111 : 11 ∙ 2 = 101 ∙ 2 = 202, 2222 : 11 ∙ 3 = 202 ∙ 3 = 606, 3333 : 11 ∙ 4 = 303 ∙ 4 = 1212, 4444 : 11 ∙ 5 = 404 ∙ 5 = 2020, 5555 : 11 ∙ 6 = 505 ∙ 6 = 3030, 6666 : 11 ∙ 7 = 606 ∙ 7 = 4242, 7777 : 11 ∙ 8 = 707 ∙ 8 = 5656, 8888 : 11 ∙ 9 = 808 ∙ 9 = 7272, 9999 : 11 ∙ 10 = 909 ∙ 10 = 9090.
Повтори алгоритм письменного умножения многозначного числа на однозначное.
Выполняем вычисления.
Первое число увеличивается к каждой строчке на 1 111, а третье число – на 1.
11 11 : 11 ∙ 2 = 101 ∙ 2 = 202
2 222 : 11 ∙ 3 = 202 ∙ 3 = 606
3 333 : 11 ∙ 4 = 303 ∙ 4 = 1 212
4 444 : 11 ∙ 5 = 404 ∙ 5 = 2 020
5 555 : 11 ∙ 6 = 505 ∙ 6 = 3 030
6 666 : 11 ∙ 7 = 606 ∙ 7 = 4 242
7 777 : 11 ∙ 8 = 707 ∙ 8 = 5 656
8 888 : 11 ∙ 9 = 808 ∙ 9 = 7 272
9 999 : 11 ∙ 10 = 909 ∙ 10 = 9 090
Оформляем задание в тетрадь.
1111 : 11 ∙ 2 = 101 ∙ 2 = 202
2222 : 11 ∙ 3 = 202 ∙ 3 = 606
3333 : 11 ∙ 4 = 303 ∙ 4 = 1212
4444 : 11 ∙ 5 = 404 ∙ 5 = 2020
5555 : 11 ∙ 6 = 505 ∙ 6 = 3030
6066 : 11 ∙ 7 = 606 ∙ 7 = 4242
7777 : 11 ∙ 8 = 707 ∙ 8 = 5656
8888 : 11 ∙ 9 = 808 ∙ 9 = 7272
9999 : 11 ∙ 10 = 909 ∙ 10 = 9090
Номер 262.
Из двух кусков ткани одинаковой ширины сшили одинаковые шторы. В первом куске было 27 м ткани, а во втором – 36 м. Из второго куска сшили на 3 шторы больше, чем из первого. Сколько штор сшили из каждого куска?
Ответ:
1) 36 − 27 = 9 (м) – на столько длиннее второй кусок ткани, чем первой к.
2) 9 : 3 = 3 (м) – ткани уходит на одну штору.
3) 27 : 3 = 9 (шт.) – штор сшили из первого куска.
4) 36 : 3 = 12 (шт.) – штор сшили из второго куска.
Ответ: 9 штор всего сшили из первого куска ткани и 12 штор всего сшили из второго куска ткани.
Повтори единицу измерения — метр.
Оформляем условие в виде таблицы.
Рассуждаем.
Вычислим, на сколько больше метров ткани во втором куске, чем в первом куске.
36 − 27 = 9 (м) — на столько длиннее второй кусок ткани, чем первый.
Продолжаем рассуждение.
Вычислим, сколько метров расходуется на одну штору.
9 : 3 = 3 (м) — ткани уходит на одну штору.
Продолжаем рассуждение.
Узнаем, сколько штор получится сшить из первого куска.
27 : 3 = 9 (шт.) — штор сшили из первого куска.
Продолжаем рассуждение.
Узнаем, сколько штор получится сшить из второго куска.
36 : 3 = 12 (шт.) — штор сшили из второго куска.
Записываем ответ.
Ответ: 9 штор сшили из первого куска ткани и 12 штор — из второго.
Номер 263.
У мальчика в коллекции было 24 болгарские марки и 40 российских марок. Он поместил их в альбом, поровну на каждую страницу. Российские марки заняли на 2 страницы больше, чем болгарские. Сколько страниц было занято российскими марками?
Ответ:
1) 40 − 24 = 16 (м) – на двух страницах.
2) 16 : 2 = 8 (м) – на странице.
3) 40 : 8 = 5 (стр) – занятых российскими марками.
Ответ: 5 страниц всего занято российскими марками.
Оформляем условие задачи в виде таблицы.
Оформляем условие.
Рассуждаем.
Вычислим, на сколько больше было российских марок.
40 − 24 = 16 (м) — на столько больше было российских марок, и они заняли две страницы.
Продолжаем рассуждение.
Вычислим, сколько марок помещается на одной странице.
16 : 2 = 8 (м) — на одной странице.
Продолжаем рассуждение.
Узнаем, сколько страниц занимают российские марки.
40 : 8 = 5 (стр.) — было занято российскими марками.
Записываем ответ.
Ответ: 5 страниц было занято российскими марками.
Номер 264.
Составь задачу по чертежу и реши её.
Из двух пунктов, расстояние между которыми 90 км, одновременно в противоположных направлениях выехали два автомобиля. Средняя скорость первого автомобиля 60 км/ч, а второго – 70 км/ч. Какое расстояние будет между ними через 4 часа?
1) 60 + 70 = 130 (км/ч) – скорость удаления автомобилей.
2) 130 ∙ 4 = 520 (км) – проедут автомобили через 4 часа.
3) 520 + 90 = 610 (км) – расстояние между пунктами в которые едут автомобили.
Ответ: расстояние между пунктами составляет 610 км.
Повтори взаимосвязь между скоростью, временем и расстоянием.
Рассмотрим схематический чертеж.
Составим задачу.
Из двух пунктов, расстояние между которыми 90 км, одновременно в противоположных направлениях выехали два автомобиля. Средняя скорость первого автомобиля 60 км/ч, а второго — 70 км/ч. Какое расстояние будет между ними через 4 часа?
Рассуждаем.
Найдем скорость удаления автомобилей, для этого сложим вместе скорость каждого.
60 + 70 = 130 (км/ч) — скорость удаления автомобилей.
Продолжаем рассуждение.
Узнаем, какое расстояние преодолеют автомобили за 4 часа., для это умножим скорость удаления на время.
130 ∙ 4 = (100 + 30) ∙ 4 = 400 + 120 = 520 (км) — проедут автомобили за 4 часа.
Продолжаем рассуждение.
Узнаем, какое расстояние будет между автомобилями через 4 часа.
520 + 90 = 610 (км) — расстояние между автомобилями.
Записываем ответ.
Ответ: 610 км будет между автомобилями через 4 часа.
Номер 265.
Выполни деление с объяснением.
Ответ:
1) 663 : 13 Для этого выделю первое неполное делимое – 66 (десятков). Нахожу первую цифру частного: 66 : 13 = 5 (десятков). Образую второе неполное делимое: 13 ∙ 5 = 65, 66 − 65 = 1 (десяток). Добавляю оставшиеся 3 единицы – 13. Нахожу вторую цифру частного: 13 : 13 = 1. Проверка:
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 65, номер 265, пример 1, 2024 год.")
Читаю ответ: при делении 663 на 13 получается 51.
2) 855 : 19
Для этого выделю первое неполное делимое – 85 (десятков).
Нахожу первую цифру частного: 85 : 19 = 4 (десятка).
Образую второе неполное делимое: 19 ∙ 4 = 76, 85 − 76 = 9 (десятков). Добавляю оставшиеся 5 единиц – 95.
Нахожу вторую цифру частного: 95 : 19 = 5.
Проверка:
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 65, номер 265, пример 2, 2024 год.")
Читаю ответ: при делении 855 на 19 получается 45.
3) 5205 : 15
Для этого выделю первое неполное делимое – 52 (сотни).
Нахожу первую цифру частного: 52 : 15 = 3 (сотни).
Образую второе неполное делимое: 15 ∙ 3 = 45, 52 − 45 = 7 (сотен). Добавляю оставшиеся 0 десятков – 70.
Нахожу вторую цифру частного: 70 : 15 = 4 (десятка).
Образую третье неполное делимое: 15 ∙ 4 = 60, 70 − 60 = 10 (сотен). Добавлю оставшиеся 5 единиц – 105.
Нахожу третью цифру частного: 105 : 15 = 7.
Проверка:
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 65, номер 265, пример 3, 2024 год.")
Читаю ответ: при делении 5205 на 15 получается 347.
4) 4608 : 18
Для этого выделю первое неполное делимое – 46 (сотен).
Нахожу первую цифру частного: 46 : 18 = 2 (сотни).
Образую второе неполное делимое: 18 ∙ 2 = 36, 46 − 36 = 10 (сотен). Добавляю оставшиеся 0 десятков – 100.
Нахожу вторую цифру частного: 100 : 18 = 5 (десятков).
Образую третье неполное делимое: 18 ∙ 5 = 90, 100 − 90 = 10 (сотен). Добавлю оставшиеся 8 единиц – 108.
Нахожу третью цифру частного: 108 : 18 = 6.
Проверка:
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 65, номер 265, пример 4, 2024 год.")
Читаю ответ: при делении 4608 на 18 получается 256.
Повтори алгоритм письменного деления на двузначные числа.
Выполним вычисления.
663 : 13 = 51
Для этого выделю первое неполное делимое — 66 (десятков).
Нахожу первую цифру частного: 66 : 13 = 5 (десятков).
Образую второе неполное делимое: 13 ∙ 5 = 65, 66 − 65 = 1 (десяток).
Добавляю оставшиеся 3 единицы — 13.
Нахожу вторую цифру частного: 13 : 13 = 1.
Проверка:
Читаю ответ: при делении 663 на 13 получается 51.
855 : 19 = 45
Для этого выделю первое неполное делимое — 85 (десятков).
Нахожу первую цифру частного: 85 : 19 = 4 (десятка).
Образую второе неполное делимое: 19 ∙ 4 = 76, 85 − 76 = 9 (десятков). Добавляю оставшиеся 5 единиц — 95.
Нахожу вторую цифру частного: 95 : 19 = 5.
Проверка:
Читаю ответ: при делении 855 на 19 получается 45.
5205 : 15 = 347
Для этого выделю первое неполное делимое — 52 (сотни).
Нахожу первую цифру частного: 52 : 15 = 3 (сотни).
Образую второе неполное делимое: 15 ∙ 3 = 45, 52 − 45 = 7 (сотен). Добавляю оставшиеся 0 десятков — 70.
Нахожу вторую цифру частного: 70 : 15 = 4 (десятка).
Образую третье неполное делимое: 15 ∙ 4 = 60, 70 − 60 = 10 (сотен). Добавлю оставшиеся 5 единиц — 105.
Нахожу третью цифру частного: 105 : 15 = 7.
Проверка:
Читаю ответ: при делении 5205 на 15 получается 347.
4608 : 18 = 256
Для этого выделю первое неполное делимое — 46 (сотен).
Нахожу первую цифру частного: 46 : 18 = 2 (сотни).
Образую второе неполное делимое: 18 ∙ 2 = 36, 46 − 36 = 10 (сотен). Добавляю оставшиеся 0 десятков — 100.
Нахожу вторую цифру частного: 100 : 18 = 5 (десятков).
Образую третье неполное делимое: 18 ∙ 5 = 90, 100 − 90 = 10 (сотен). Добавлю оставшиеся 8 единиц — 108.
Нахожу третью цифру частного: 108 : 18 = 6.
Проверка:
Читаю ответ: при делении 4608 на 18 получается 256.
Оформим задание в тетрадь.
Номер 266.
Ответ:
Повтори алгоритм письменного деления на двузначные числа.
Выполним вычисления.
9975 : 75 = 133
Для этого выделю первое неполное делимое — 99 (сотен).
Нахожу первую цифру частного: 99 : 75 = 1 (сотня).
Образую второе неполное делимое: 75 ∙ 1 = 75, 99 − 75 = 24 (сотни). Добавляю оставшиеся 7 десятков — 247.
Нахожу вторую цифру частного: 247 : 75 = 3 (десятка).
Образую третье неполное делимое: 75 ∙ 3 = 225, 247 − 225 = 22 (сотен). Добавлю оставшиеся 5 единиц — 225.
Нахожу третью цифру частного: 225 : 75 = 3.
Читаю ответ: при делении 9975 на 75 получается 133.
2544 : 53 = 48
Для этого выделю первое неполное делимое — 254 (десятка).
Нахожу первую цифру частного: 254 : 53 = 4 (десятка).
Образую второе неполное делимое: 53 ∙ 4 = 212, 254 − 212 = 42 (десятка). Добавляю оставшиеся 4 единицы — 424.
Нахожу вторую цифру частного: 424 : 53 = 8.
Читаю ответ: при делении 2544 на 53 получается 48.
(890 – 43) ∙ 90 + 375 = 76605
В данном выражении сначала выполняется действие в скобках — вычитание, затем действия за скобками: умножение, а потом — сложение.
1) 890 – 43 = 840 + 50 – 43 = 840 + 7 = 847
2) 847 ∙ 90 = 76230
3) 76230 + 375 = 76605
Оформим задание в тетрадь.
Номер 267.
Выполни деление с остатком и проверь.
Ответ:
Повтори, как выполнять деление с остатком, и как делать проверку.
Выполним вычисления и сделаем проверку.
457 : 58 = 7 (ост. 51)
Разделю 457 не на 58, а на 60, чтобы легче было найти цифру частного. Для этого разделю 45 на 6, получу 7. Это пробное число, его нельзя сразу записать в частном — сначала надо проверить.
Умножу 58 на 7, получится 406, остаток 51.
Сравню остаток с делителем: число 51 меньше, чем 58. Значит, число 7 подходит. Теперь его можно записать в частном.
Проверка:
1) 51 < 58
2) 58 ∙ 7 + 51 = 406 + 51 = 457
272 : 98 = 2 (ост. 76)
Разделю 272 не на 98, а на 100, чтобы легче было найти цифру частного. Для этого разделю 2 на 1, получу 2. Это пробное число, его нельзя сразу записать в частном — сначала надо проверить.
Умножу 98 на 2, получится 196, остаток 76.
Сравню остаток с делителем: число 76 меньше, чем 98. Значит, число 2 подходит. Теперь его можно записать в частном.
Проверка:
1) 76 < 98
2) 98 ∙ 2 + 76 = 196 + 76 = 272
495 : 46 = 10 (ост. 35)
Выделю первое неполное делимое — 49 (десятков).
Нахожу первую цифру частного: 49 : 46 = 1 (десяток).
Образую второе неполное делимое: 46 ∙ 1 = 46, 49 − 46 = 3 (десятка). Добавляю оставшиеся 5 единиц — 35.
Нахожу вторую цифру частного: 35 : 46 = 0, так как 35 < 46.
Значит, в частном 10, а остаток 35.
Проверка:
1) 35 < 46
2) 46 ∙ 10 + 35 = 460 + 35 = 495
385 : 65 = 5 (ост. 60)
Разделю 385 не на 65, а на 70, чтобы легче было найти цифру частного. Для этого разделю 38 на 7, получу 5. Это пробное число, его нельзя сразу записать в частном — сначала надо проверить.
Умножу 65 на 5, получится 325, остаток 60.
Сравню остаток с делителем: число 60 меньше, чем 65. Значит, число 5 подходит. Теперь его можно записать в частном.
Проверка:
1) 60 < 65
2) 65 ∙ 5 + 60 = 325 + 60 = 385
321 : 47 = 6 (ост. 39)
Разделю 321 не на 47, а на 50, чтобы легче было найти цифру частного. Для этого разделю 32 на 5, получу 6. Это пробное число, его нельзя сразу записать в частном — сначала надо проверить.
Умножу 47 на 6, получится 282, остаток 39.
Сравню остаток с делителем: число 39 меньше, чем 47. Значит, число 6 подходит. Теперь его можно записать в частном.
Проверка:
1) 39 < 47
2) 47 ∙ 6 + 39 = 282 + 39 = 321
Оформим задание в тетрадь.
Номер 268.
Реши уравнения, в которых неизвестное число можно найти вычитанием.
Ответ:
х − 480 = 520
х − уменьшаемое.
Чтобы найти неизвестное уменьшаемое, нужно к вычитаемому прибавить разность.
Решается сложением.
Не подходит.
290 + х = 760
х − второе слагаемое.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Решается вычитанием.
Подходит.
х = 760 − 290
х = 470
540 − х = 260
х − вычитаемое.
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
Решается вычитанием.
Подходит.
х = 540 − 260
х = 280
х − 420 = 20
х − уменьшаемое.
Чтобы найти неизвестное уменьшаемое, нужно к вычитаемому прибавить разность.
Решается сложением.
Не подходит.
х + 370 = 600
х − неизвестное слагаемое.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Решается вычитанием.
Подходит.
х = 600 − 370
х = 230
900 − х = 850
х − неизвестное вычитаемое.
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
Решается вычитанием.
Подходит.
х = 900 − 850
х = 50
Повтори, как решать уравнения.
Рассуждаем.
х − 480 = 520
х — уменьшаемое.
Чтобы найти неизвестное уменьшаемое, нужно к вычитаемому прибавить разность.
Решается сложением.
Не подходит.
290 + х = 760
х — второе слагаемое.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Решается вычитанием.
Подходит.
х = 760 − 290
х = 470
540 − х = 260
х — вычитаемое.
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
Решается вычитанием.
Подходит.
х = 540 − 260
х = 280
х − 420 = 20
х — уменьшаемое.
Чтобы найти неизвестное уменьшаемое, нужно к вычитаемому прибавить разность.
Решается сложением.
Не подходит.
х + 370 = 600
х — неизвестное слагаемое.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Решается вычитанием.
Подходит.
х = 600 − 370
х = 230
900 − х = 850
х — неизвестное вычитаемое.
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
Решается вычитанием.
Подходит.
х = 900 − 850
х = 50
Оформим задание в тетрадь.
х – 480 = 520 — решается сложением
290 + х = 760 — решается вычитанием
х = 760 – 290
х = 470
540 – х = 260 — решается вычитанием
х = 540 – 260
х = 280
х – 420 = 20 — решается сложением
х + 370 = 600 — решается вычитанием
х = 600 – 370
х = 230
900 – х = 850 — решается вычитанием
х = 900 – 850
х = 50
Номер 269.
Ответ:
1) 2 т − 8 ц = 20 ц − 8 ц = 12 ц
2 ч − 8 мин = 120 мин − 8 мин = 112 мин = 1 ч 52 мин
450 кг + 900 кг = 1350 кг = 1 т 350 кг
820 м + 600 м = 1420 м
2 мин − 40 с = 120 с − 40 с = 80 с = 1 мин 20 с
5 дм − 8 см = 50 см − 8 см = 42 см = 4 дм 2 см
2) 46 мм² + 54 мм² = 100 мм² = 1 см²
82 см² + 118 см² = 200 см² = 2 дм²
4 дм² − 25 см² = 400 см² − 25 см² = 375 см² = 3 дм² 75 см²
3 м² − 67 дм² = 300 дм² − 67 дм² = 233 дм² = 2 м² 33 дм²
Повтори единицы массы, длины и времени, а также единицы площади.
Выполняем вычисления.
Так как 1 т = 10 ц, то
2 т – 8 ц = 20 ц – 8 ц = 12 ц
Так как 1 ч = 60 мин, то
2 ч – 8 мин = 2 ∙ 60 мин – 8 мин = 120 мин – 8 мин = 112 мин = 1 ч 52 мин
Так как 1 т = 1000 кг, то
450 кг + 900 кг = 1350 кг = 1 т 350 кг
Так как 1 км = 1000 м, то
820 м + 600 м = 1420 м = 1 км 420 м
Так как 1 мин = 60 с, то
2 мин – 40 с = 2 ∙ 60 с – 40 с = 120 с – 40 с = 80 с = 1 мин 20 с
Так как 1 дм = 10 см, то
5 дм – 8 см = 5 ∙ 10 см – 8 см = 50 см – 8 см = 42 см = 4 дм 2 см
Так как 1 см² = 100 мм², то
46 мм² + 54 мм² = 46 мм² + 4 мм² + 50 мм² = 50 мм² + 50 мм² = 100 мм² = 1 см²
Так как 1 дм² = 100 см², то
82 см² + 118 см² = 82 см² + 18 см² + 100 см² = 100 см² + 100 см² = 200 см² = 2 дм²
Так как 1 дм² = 100 см², то
4 дм² − 25 см² = 400 см² − 25 см² = 300 см² + 100 см² − 25 см² = 300 см² + 75 см² = 375 см² = 3 дм² 75 см²
Так как 1 м² = 100 дм², то
3 м² − 67 дм² = 300 дм² − 67 дм² = 200 дм² + 100 дм² − 67 дм² = 200 дм² + 33 дм² = 233 дм² = 2 м² 33 дм²
Оформляем задание в тетрадь.
2 т − 8 ц = 20 ц − 8 ц = 12 ц
2 ч − 8 мин = 120 мин − 8 мин = 112 мин = 1 ч 52 мин
450 кг + 900 кг = 1350 кг = 1 т 350 кг
820 м + 600 м = 1420 м = 1 км 420 м
2 мин − 40 с = 120 с − 40 с = 80 с = 1 мин 20 с
5 дм − 8 см = 50 см − 8 см = 42 см = 4 дм 2 см
46 мм² + 54 мм² = 100 мм² = 1 см²
82 см² + 118 см² = 200 см² = 2 дм²
4 дм² − 25 см² = 400 см² − 25 см² = 375 см² = 3 дм² 75 см²
3 м² − 67 дм² = 300 дм² − 67 дм² = 233 дм² = 2 м² 33 дм²
Номер 270.
Нина на 3 см ниже Димы, а Дима на 4 см ниже Кости. Запиши имена детей в порядке увеличения их роста.
Ответ:
Рост Нины = рост Димы - 3
Рост Димы = рост Кости - 4
Получается, что рост Димы относительно Нины = рост Нины + 3, а рост Кости относительно Димы = рост Димы + 4, получается, рост Кости - рост Нины = 7.
Приведем рост ребят к росту Кости и сравним:
Нина + 7 = Костя
Дима + 4 = Костя
Костя = Костя
Ответ: Нина, Дима, Костя.
Повтори единицу длины — сантиметр.
Оформляем условие в виде краткой записи.
Рассуждаем.
Рост Нины = рост Димы – 3 см
Рост Димы = рост Кости – 4 см
Получается, что
Рост Димы = рост Нины + 3 см
Рост Кости = рост Димы + 4 см,
Значит, рост Кости = рост Нины + 7 см.
Следовательно, Костя выше Нины и Димы, а Дима выше Нины.
Записываем ответ.
Ответ: Нина, Дима, Костя.
Задание внизу страницы
Ответ:
Повтори алгоритм письменного деления на двузначные числа.
Выполняем вычисления.
2418 : 62 = 39
Для этого выделю первое неполное делимое — 241 (десяток).
Нахожу первую цифру частного: 241 : 62 = 3 (десятка).
Образую второе неполное делимое: 62 ∙ 3 = 186, 241 − 186 = 55 (десятков). Добавляю оставшиеся 8 единиц — 558.
Нахожу вторую цифру частного: 558 : 62 = 9.
Читаю ответ: при делении 2418 на 62 получается 39.
3312 : 92 = 36
Для этого выделю первое неполное делимое — 331 (десяток).
Нахожу первую цифру частного: 331 : 92 = 3 (десятка).
Образую второе неполное делимое: 92 ∙ 3 = 276, 331 − 276 = 55 (десятков). Добавляю оставшиеся 2 единицы — 552.
Нахожу вторую цифру частного: 552 : 92 = 6.
Читаю ответ: при делении 3312 на 92 получается 36.
(867 + 573) : 40 ∙ 123 = 4428
В данном выражении сначала выполняется действие в скобках — сложение, затем деление, а потом — умножение.
1) 867 + 573 = 1440
2) 1440 : 40 = 36
3) 123 ∙ 36 = 4428
Оформляем задание в тетрадь.
Задание на полях страницы
Найди площади фигур.
Разобьем фигуры на клетки и сосчитаем их площадь:
Площадь желтой фигуры целиком (квадрат + вырезанная часть) = 36 клеток.
Площадь вырезанной части = 4 целые клеточки и 8 половинок, значит всего 8 клеток (потому что 1 клетка = 2 половинки).
Площадь желтой фигуры: 36 клеток – 8 клеток = 28 клеток или 7 см2.
Площадь розовой фигуры вместе с вырезанной частью = 36 клеток = 9 см2.
Площадь вырезанной части – 6 клеток = 1 см2 и 50 мм2.
Площадь розовой фигуры: 36 клеток – 6 клеток = 30 клеток = 7 см2 50 мм2.
Ответ: 7 см2 и 7 см2 50 мм2.
Повтори, как найти площадь фигуры.
Рассмотрим фигуры на полях.
Найдем площади данных фигур.
Разобьем фигуры на клетки и сосчитаем их площадь:
Площадь желтой фигуры целиком (квадрат + вырезанная часть) = 36 клеток.
Площадь вырезанной части = 4 целые клеточки и 8 половинок, значит всего 8 клеток (потому что 1 клетка = 2 половинки).
Площадь желтой фигуры: 36 клеток − 8 клеток = 28 клеток или 7 см².
Площадь розовой фигуры вместе с вырезанной частью = 36 клеток = 9 см².
Площадь вырезанной части – 6 клеток = 1 см² и 50 мм².
Площадь розовой фигуры: 36 клеток − 6 клеток = 30 клеток = 7 см² 50 мм².
Запишем ответ.
Ответ: 7 см² и 7 см² 50 мм².
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽
Напишите свой комментарий.