Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 58

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Задание вверху страницы.
Объясни как выполнено деление с остатком.
Ответ:
Пишу: 324 : 62. Разделю 324 не на 62, а на 60, чтобы легче было найти цифру частного. Для этого разделю 32 на 6, получу 5. Это пробное число, его нельзя сразу записать в частном - сначала надо проверить. Умножу 62 на 5, получится 310, остаток 14. Сравню остаток с делителем: число 14 меньше, чем 62. Значит, число 5 подходит. Теперь его можно записать в частном.
Пишу: 526 : 74. Разделю 526 не на 74, а на 70, чтобы легче было найти цифру частного. Для этого разделю 52 на 7, получу 7. Это пробное число, его нельзя сразу записать в частном - сначала надо проверить. Умножу 74 на 7, получится 518, остаток 8. Сравню остаток с делителем: число 8 меньше, чем 74. Значит, число 7 подходит. Теперь его можно записать в частном.
Пишу: 793 : 83. Разделю 793 не на 83, а на 80, чтобы легче было найти цифру частного. Для этого разделю 79 на 8, получу 9. Это пробное число, его нельзя сразу записать в частном - сначала надо проверить. Умножу 83 на 9, получится 747, остаток 46. Сравню остаток с делителем: число 46 меньше, чем 83. Значит, число 9 подходит. Теперь его можно записать в частном.
Номер 211.
Найди частное и остаток, проверь решение.
Ответ:
Повтори алгоритм письменного деления на двузначные числа.
Выполняем вычисления с пояснениями.
Пишу: 156 : 48.
Разделю 156 не на 48, а на 40, чтобы легче было найти цифру частного. Для этого разделю 15 на 4, получу 3. Это пробная цифра, её нельзя сразу записать в частном – сначала надо проверить, подходит ли цифра 3.
Умножу 48 на 3, получится 144, остаток 12.
Сравню остаток с делителем: число 12 меньше, чем 48. Значит, цифра 3 подходит. Теперь её можно записать в частном.
Пишу: 278 : 62.
Разделю 278 не на 62, а на 60, чтобы легче было найти цифру частного. Для этого разделю 27 на 6, получу 4. Это пробная цифра, её нельзя сразу записать в частном – сначала надо проверить, подходит ли цифра 4.
Умножу 62 на 4, получится 248, остаток 30.
Сравню остаток с делителем: число 30 меньше, чем 62. Значит, цифра 4 подходит. Теперь её можно записать в частном.
Пишу: 346 : 56.
Разделю 346 не на 56, а на 50, чтобы легче было найти цифру частного. Для этого разделю 34 на 5, получу 6. Это пробная цифра, её нельзя сразу записать в частном – сначала надо проверить, подходит ли цифра 6.
Умножу 56 на 6, получится 336, остаток 10.
Сравню остаток с делителем: число 10 меньше, чем 56. Значит, цифра 6 подходит. Теперь её можно записать в частном.
Пишу: 445 : 73.
Разделю 445 не на 73, а на 70, чтобы легче было найти цифру частного. Для этого разделю 44 на 7, получу 6. Это пробная цифра, её нельзя сразу записать в частном – сначала надо проверить, подходит ли цифра 6.
Умножу 73 на 6, получится 438, остаток 7.
Сравню остаток с делителем: число 7 меньше, чем 73. Значит, цифра 6 подходит. Теперь её можно записать в частном.
Проверка деления с остатком:
1) Остаток меньше делителя;
2) Если частное умножить на делитель и к полученному произведению прибавить остаток, то в результате вычислений должно получится делимое.
Оформляем задание в тетрадь.

Номер 212.
Космонавты были в полёте 290 ч. Сколько это суток и часов?
Ответ:В 1 сутках 24 часа.

Повтори единицы времени – сутки и час.
Выполняем вычисления.
В 1 сутках 24 часа.
290 ч : 24 = 12 сут. 2 ч
Ответ: 12 сут. 2 ч
Оформляем задание в тетрадь.
В 1 сутках 24 часа.
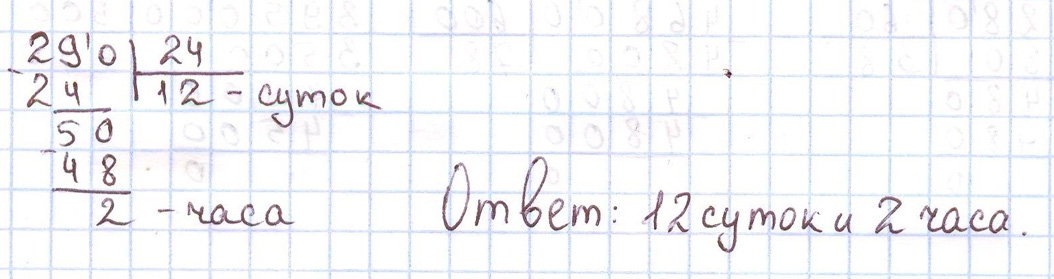
Номер 213.
Площадь первого участка 120 м², второго 160 м². При одинаковой норме высева на 1 м² на первом участке высеяли семян ржи на 1 кг меньше, чем на втором. Объясни, что означают выражения:
160 - 120
1000 : (160 - 120)
1000 : (160 - 120) * 160

1000 : (160 − 120) = 1000 : 40 = 25 грамм – число семян ржи на 1 м².
1000 : (160 − 120) ∙ 160 = 4 кг – столько семян ржи высадили на второй участок.
Повтори единицы массы – килограмм и грамм, а также единицы площади.
Оформляем условие в виде таблицы.

Рассуждаем.
Объясним, что означают выражения:
160 − 120 = 40 – насколько S первого уч. меньше S второго участка.
1000 : (160 − 120) = 1000 : 40 = 25 грамм – число семян ржи на 1 м².
1000 : (160 − 120) ∙ 160 = 4 кг – столько семян ржи высадили на второй участок.
Номер 214.
В международном автопробеге участвовало 350 машин. Экипаж каждой машины состоял из трёх спортсменов. До финиша не дошли 105 машин. Сколько машин и сколько спортсменов прибыли к финишу?
Ответ:

1) 350 - 105 = 245 (м.) - доехало до финиша
2) 3 * 245 = 735 (сп.) - доехало до финиша.
Способ решения 2:
1) 3 * 350 = 1050 (сп.) в 350 машинах участвовали
2) 3 * 105 = 315 (сп.) в 105 машинах д=не дошли до финиша
3) 1050 - 315 = 735 (сп.) - прибыли к финишу
4) 350 - 105 = 245 (шт.) - машин пришли к финишу
Ответ: 245 машин всего пришли к финишу и 735 спортсменов прибыли к финишу.
Повтори алгоритм вычитания и умножения трёхзначных чисел, а также способы оформления краткой записи к задаче.
Оформляем условие в виде краткой записи.
Участвовала − 350 м. по 3 сп.
Не дошло − 105 м. по 3 сп.
Дошло − ? м. ? сп.
Рассуждаем.
Узнаем, сколько машин доехали до финиша, для этого из всего количества машин вычтем количество тех, которые до финиша не дошли.
1) 350 − 105 = 245 (м.) – доехало до финиша.
Продолжаем рассуждение.
Узнаем, сколько спортсменов доехали до финиша, для этого количество машин, доехавших до финиша, умножим на 3.
2) 245 ∙ 3 = 735 (сп.) – доехало до финиша.
Записываем ответ.
Ответ: 245 машин и 735 спортсменов.
Номер 215.
Составь по задачам уравнения и реши их.
1) Какое число надо уменьшить на 28, чтобы получить число, равное сумме чисел 58 и 37?
2) Какое число надо увеличить в 8 раз, чтобы получить число, равное произведению чисел 80 и 12?
3) Какое число надо уменьшить в 28 раз, чтобы получить число, равное разности чисел 300 и 203?
1) х − 28 = 58 + 37
х − 28 = 95
х = 95 + 28
х = 123
Ответ: х = 123
2) х ∙ 8 = 80 ∙ 12
х ∙ 8 = 960
х = 960 : 8
х = 120
Ответ: х = 120
3) х : 28 = 300 − 203
х : 28 = 97
х = 97 ∙ 28
х = 2716
Ответ: х = 2716
Повтори, как решать уравнения.
Составляем уравнения по данным задачам и выполняем вычисления с пояснением.
В каждом из уравнений сначала выполняем вычисления в правой части.
1. Чтобы найти уменьшаемое, нужно к разности прибавить вычитаемое:
95 + 28 = 123.
Проверка:
123 – 28 = 58 + 37
95 = 95
2. Чтобы найти первый множитель, нужно произведение разделить на второй множитель:
960 : 8 = 120.
Проверка:
120 ∙ 8 = 80 ∙ 12
960 = 960
3. Чтобы найти делимое, нужно частное умножить на делитель:
97 ∙ 28 = 2 716.
Проверка:
2 716 : 28 = 300 – 203
97 = 97
Оформляем задание в тетрадь.
1) х − 28 = 58 + 37
х − 28 = 95
х = 95 + 28
х = 123
Проверка:
123 – 28 = 58 + 37
95 = 95
Ответ: х = 123
2) х ∙ 8 = 80 ∙ 12
х ∙ 8 = 960
х = 960 : 8
х = 120
Проверка:
120 ∙ 8 = 80 ∙ 12
960 = 960
Ответ: х = 120
3) х : 28 = 300 − 203
х : 28 = 97
х = 97 ∙ 28
х = 2716
Проверка:
2716 : 28 = 300 – 203
97 = 97
Ответ: х = 2716
Номер 216.
Ответ:
Повтори алгоритм письменного деления на двузначное число и порядок действий.
Выполняем вычисления с пояснениями.
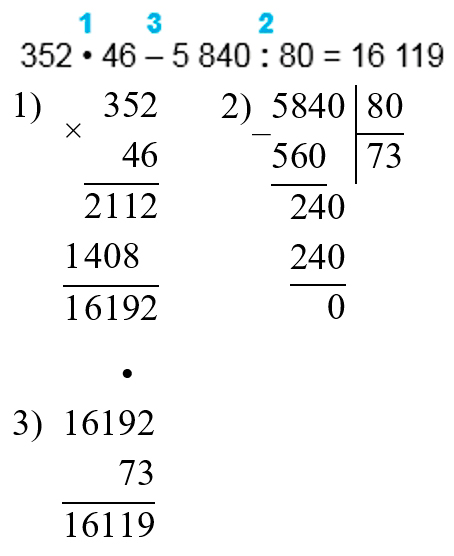
Пишу: 384 : 96.
Разделю 384 не на 96, а на 90, чтобы легче было найти цифру частного. Для этого разделю 38 на 9, получу 4. Это пробная цифра, её нельзя сразу записать в частном – сначала надо проверить, подходит ли цифра 4.
Умножу 96 на 4, получится 384, значит, цифра 4 подходит. Теперь её можно записать в частном.
Пишу: 192 : 48.
Разделю 192 не на 48, а на 40, чтобы легче было найти цифру частного. Для этого разделю 19 на 4, получу 4. Это пробная цифра, её нельзя сразу записать в частном – сначала надо проверить, подходит ли цифра 4.
Умножу 48 на 4, получится 192, значит, цифра 4 подходит. Теперь её можно записать в частном.
Пишу: 648 : 72.
Разделю 648 не на 72, а на 70, чтобы легче было найти цифру частного. Для этого разделю 64 на 7, получу 9. Это пробная цифра, её нельзя сразу записать в частном – сначала надо проверить, подходит ли цифра 9.
Умножу 72 на 9, получится 648, значит, цифра 9 подходит. Теперь её можно записать в частном.
Оформляем задание в тетрадь.

Номер 217.
Найди значения выражений 360 : с и 360 ∙ с, если с = 1; с = 3; с = 4; с = 6; с = 10. Наблюдай, как при этом изменяется частное, как изменяется произведение.
Ответ:
360 : с
360 : 1 = 360
360 : 3 = 120
360 : 4 = 90
360 : 6 = 60
360 : 10 = 36
360 ∙ с
360 ∙ 1 = 360
360 ∙ 3 = 1080
360 ∙ 4 = 1440
360 ∙ 6 = 2160
360 ∙ 10 = 3600
Частное все время уменьшается, а произведение – наоборот увеличивается.
Повтори, что такое буквенные выражения, а также как называются числа при умножении и делении.
Найдем значения выражений 360 : с.
360 : с, если с = 1; с = 3; с = 4; с = 6; с = 10.
360 : 1 = 360
360 : 3 = 120
360 : 4 = 90
360 : 6 = 60
360 : 10 = 36
Найдем значения выражений 360 ∙ с.
360 ∙ с, если с = 1; с = 3; с = 4; с = 6; с = 10.
360 ∙ 1 = 360
360 ∙ 3 = 1080
360 ∙ 4 = 1440
360 ∙ 6 = 2160
360 ∙ 10 = 3600
Вывод.
Частное все время уменьшается, а произведение – наоборот увеличивается.
Номер 218.
Выложи из палочек такую фигуру. Какие углы в этой фигуре? Переложи 4 палочки так, чтобы получилось два остроугольных треугольника. Будут ли эти треугольники равнобедренными? равносторонними?


Повтори, какие бывают углы и треугольники.
Выложим из палочек данную фигуру.
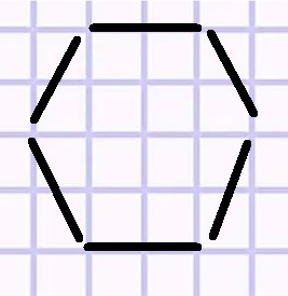
Углы в этой фигуре тупые. Переложим 4 палочки так, чтобы получилось 2 остроугольных треугольника.
Переложим палочки, как сказано в задании.
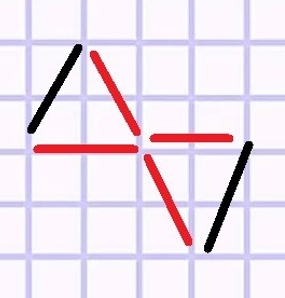
Данные треугольники равносторонние, потому что длина палочек одинаковая и равнобедренные, потому что две стороны у таких треугольников точно равны.
Задание внизу страницы
Ответ:
Повтори алгоритм письменного деления на двузначное число и порядок действий.
Выполняем вычисления с пояснениями.

Пишу: 399 : 57.
Разделю 399 не на 57, а на 50, чтобы легче было найти цифру частного. Для этого разделю 39 на 5, получу 7. Это пробная цифра, её нельзя сразу записать в частном – сначала надо проверить, подходит ли цифра 7.
Умножу 57 на 7, получится 399, значит, цифра 7 подходит. Теперь её можно записать в частном.
Пишу: 236 : 59.
Разделю 236 не на 59, а на 50, чтобы легче было найти цифру частного. Для этого разделю 23 на 5, получу 4. Это пробная цифра, её нельзя сразу записать в частном – сначала надо проверить, подходит ли цифра 4.
Умножу 59 на 4, получится 236, значит, цифра 4 подходит. Теперь её можно записать в частном.
Пишу: 475 : 95.
Разделю 475 не на 95, а на 90, чтобы легче было найти цифру частного. Для этого разделю 47 на 9, получу 5. Это пробная цифра, её нельзя сразу записать в частном – сначала надо проверить, подходит ли цифра 5.
Умножу 95 на 5, получится 475, значит, цифра 5 подходит. Теперь её можно записать в частном.
Оформляем задание в тетрадь.
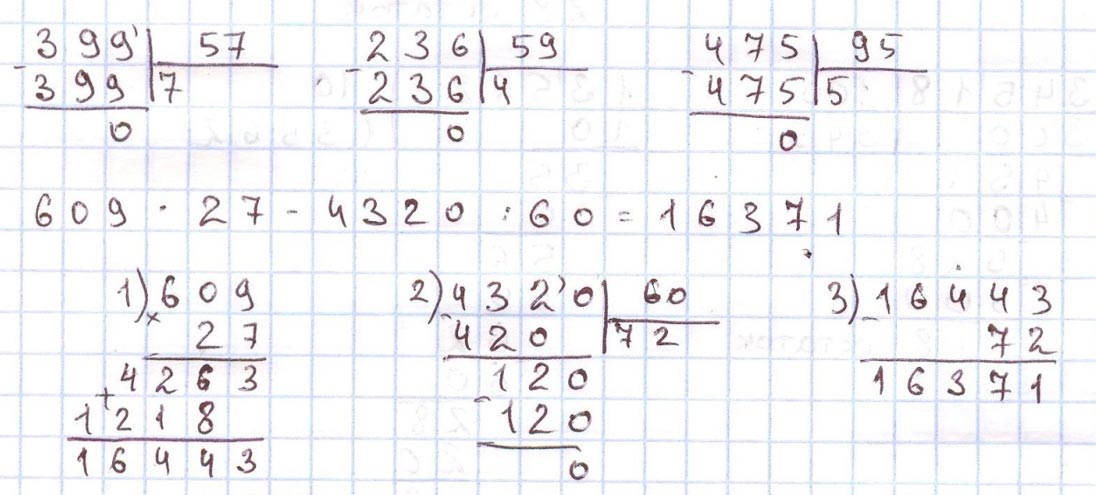
Задание на полях страницы
Магический квадрат.


100 + 90 + 140 = 100 + 100 + 130 = 330
150 + 110 + 70 = 150 + 180 = 330
80 + 130 + 120 = 200 + 130 = 330
100 + 150 + 80 = 180 + 150 = 330
90 + 110 + 130 = 200 + 130 = 330
140 + 70 + 120 = 140 + 190 = 330
100 + 110 + 120 = 300 + 30 = 330
80 + 110 + 140 = 190 + 140 = 330
Магический квадрат – таблица, заполненная различными числами таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях одинакова.
Выполняем вычисления.
140 + 110 + 80 = 330
330 – (100 + 110) = 120
330 – (140 + 120) = 70
330 – (110 + 70) = 50
330 – (120 + 80) = 130
330 – (130 + 110) = 90
Оформляем задание в тетрадь.
Номер 22.
От двух пристаней, расстояние между которыми 350 км, в 11 ч отправились навстречу друг другу два теплохода. Скорость первого 32 км/ч, скорость второго 38 км/ч. В какое время теплоходы встретятся?
Ответ:
1) 32 + 38 = 70 (км/ч) – скорость сближения.
2) 350 : 70 = 5 (ч) – теплоходы были в пути.
3) 11 + 5 = 16 (ч) – время, когда теплоходы встретятся.
Ответ: теплоходы встретятся в 16 часов.
Номер 23.
Два велосипедиста отправились из одного посёлка одновременно в противоположных направлениях. Через 30 мин расстояние между ними было 15 км. Скорость одного из них 260 м/мин. Узнай скорость другого велосипедиста. Составь и реши задачи, обратные данной.
Ответ:
15 км = 15000 м
1) 260 ∙ 30 = 7800 (м) – проехал один велосипедист.
2) 15000 − 7800 = 7200 (м) – проехал другой велосипедист.
3) 7200 : 30 = 240 (м/мин) – скорость другого велосипедиста.
Ответ: скорость другого велосипедиста составляет 240 м/мин.
Обратная задача 1:
Два велосипедиста одновременно отправились из одного поселка в противоположных направлениях. Средняя скорость одного из них 260 м / мин, а другого – 240 м/ мин. Какое расстояние будет между ними через 30 мин? Вырази расстояние между ними через 30 минут в километрах.
.jpg)
1) 260 + 240 = 500 (м/мин) – скорость удаления.
2) 500 ∙ 30 = 15000 (м) = 15 км – расстояние между велосипедистами через 30 минут езды.
Ответ: 15 км.
Обратная задача 2:
Два велосипедиста одновременно отправились из поселка в противоположных направлениях. Скорость одного из них 260 м/мин, а скорость другого 240 м/мин. Через сколько минут расстояние между ними будет 15 км?
.jpg)
15 км = 15000 м
1) 260 + 240 = 500 (м/мин) – скорость удаления.
2) 15000 : 500 = 30 (мин) – время, через которое расстояние между велосипедистами будет равно 15 км.
Ответ: через 30 минут расстояние между велосипедистами составит 15 км.
Номер 24.
В санатории построили бассейн прямоугольной формы, длина которого 30 м, ширина 5 м и глубина 2 м.
1) Сколько квадратных кафельных плиток со стороной 1 дм каждая потребовалось для облицовки дна этого бассейна? стенок этого бассейна?
2) Сколько надо сделать шагов, чтобы обойти весь бассейн, если длина шага 50 см?
3) За какое время можно обойти бассейн со всех сторон, если идти со скоростью 35 м/мин?
Длина – 30 м
Ширина – 5 м
Глубина – 2 м
Сторона плиток – 1 дм
Кол-во плиток – ?
Задача 1:
Пояснение: Стены у бассейна попарно равны, то есть две противоположные стены равны.
Длина – 30 м
Ширина – 5 м
Глубина – 2 м
Сторона плиток – 1 дм
Кол-во плиток – ?
1) 1 ∙ 1 = 1 (дм²) – площадь одной плитки для облицовки бассейна;
2) 30 ∙ 5 = 150 (м²) = 15 000 (дм2) – площадь дна бассейна;
3) 15 000 ∙ 1 = 15 000 (кафельных плиток) – понадобится для облицовки дна бассейна;
4) 5 ∙ 2 = 10 (м²) – площадь 1ой и 3ей стенок бассейна;
5) 30 ∙ 2 = 60 (м²) – площадь 2ой и 4ой стенок бассейна;
6) 10 · 2 + 60 · 2 = 20 + 120 = 140 (м2) = 14 000 (дм2) – площадь стенок бассейна;
7) 14 000 ∙ 1 = 14 000 (кафельных плиток) – понадобятся для облицовки стенок бассейна.
Ответ: 15 000 плиток всего понадобится для облицовки дна бассейна и 14 000 плиток всего понадобится для облицовки стенок бассейна.
Задача 2:
Пояснение: Человеку нужно обойти бассейн, а значит нужно обойти его по бордюру, который имеет форму прямоугольника. Чтобы узнать сколько шагов нужно сделать, нужно прежде всего найти длину всего бордюра, а значит посчитать его периметр.
Длина – 30 м
Ширина – 5 м
Длина шага – 50 см
Кол-во шагов – ?
1) (30 + 5) ∙ 2 = 35 · 2 = 70 (м) = 7000 (см) – периметр бассейна;
2) 7000 : 50 = 140 (шагов) – нужно сделать, чтобы обойти весь бассейн.
Ответ: 140 шагов.
Задача 3:
Периметр – 70 м
Скорость – 35 м/мин
Время – ?
70 : 35 = 2 (мин) – потребуется, чтобы обойти весь бассейн.
Ответ: 2 минуты всего потребуется, чтобы обойти весь бассейн.
Номер 25.
Составь по данной таблице выражения, которые показывают:
1) стоимость всех купленных столов и стульев;
2) на сколько больше стоимость всех стульев, чем стоимость всех столов;
3) стоимость всех столов и шести стульев.

1) 8 ∙ а + 36 ∙ к;
2) 36 ∙ к − 8 ∙ а;
3) 8 ∙ а + 6 ∙ к.
Номер 26.
Назови предметы, которые имеют форму цилиндра, куба, конуса.
Ответ:
Цилиндр – стакан, труба.
Куб – игральный кубик, коробка.
Конус – пожарное ведро, рожок от мороженного.
Номер 1.
Объясни на примере, как можно по-разному умножить число на сумму.
Ответ:4 ∙ (5 + 3) = 4 ∙ 8 = 32 4 ∙ (5 + 3) = 4 ∙ 5 + 4 ∙ 3 = 20 + 12 = 32
Номер 2.
Составь примеры на умножение двузначного числа на двузначное и трёхзначного числа на трёхзначное. Реши их с объяснением.
Ответ:1) 12 ∙ 37

Умножу первый множитель на число единиц:
12 ∙ 5 = 60
Получу первое неполное произведение 60.
Умножу первый множитель на число десятков:
12 ∙ 3 = 36
Начну записывать первое неполное произведение под единицами, а второе под десятками.
Сложу неполные произведения.
Читаю ответ: произведение чисел 12 и 35 равно 420.
2) 254 ∙ 937
.jpg)
Умножу первый множитель на число единиц: 123 ∙ 7 = 861 Получу первое неполное произведение 861. Умножу первый множитель на число десятков: 123 ∙ 8 = 984 Получу второе неполное произведение: 984. Умножу первый множитель на число сотен: 123 ∙ 9 = 1107 Начну подписывать первое неполное произведение под единицами,а второе неполное произведение под десятками. Третье неполное произведение записываю под сотнями. Сложу неполные произведения. Читаю ответ: произведение чисел 123 и 789 равно 121401.
Задание на полях страницы
Начерти такой узор.
Ответ:
1. Нарисуй в ряд по вертикали 4 кружка, диаметр каждого из которых 2 см. 2. Внутри каждого нарисуй ромб так, чтобы они соприкасались кончиками и образовывали гирлянду сверху вниз. Длина ромба 2 см, а ширина 1 см. 3. В точке, где мысленно проведенная длина и ширина пересекаются поставь точку - это начало другой цепочки из ромбов уже другого цвета. Строй их также как и предыдущую цепочку (ширина 1 см, а длина - 2 см. 4. Сверху и снизу дорисуй перекладинки ромба, чтобы они касались круга.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.