Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 56
- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Номер 22.
От двух пристаней, расстояние между которыми 350 км, в 11 ч отправились навстречу друг другу два теплохода. Скорость первого 32 км/ч, скорость второго 38 км/ч. В какое время теплоходы встретятся?
Ответ:
1) 32 + 38 = 70 (км/ч) – скорость сближения.
2) 350 : 70 = 5 (ч) – теплоходы были в пути.
3) 11 + 5 = 16 (ч) - теплоходы встретятся
Ответ: в 16 часов теплоходы встретятся.
Повтори взаимосвязь между скоростью, временем и расстоянием.
Оформляем условие в виде схематического чертежа.
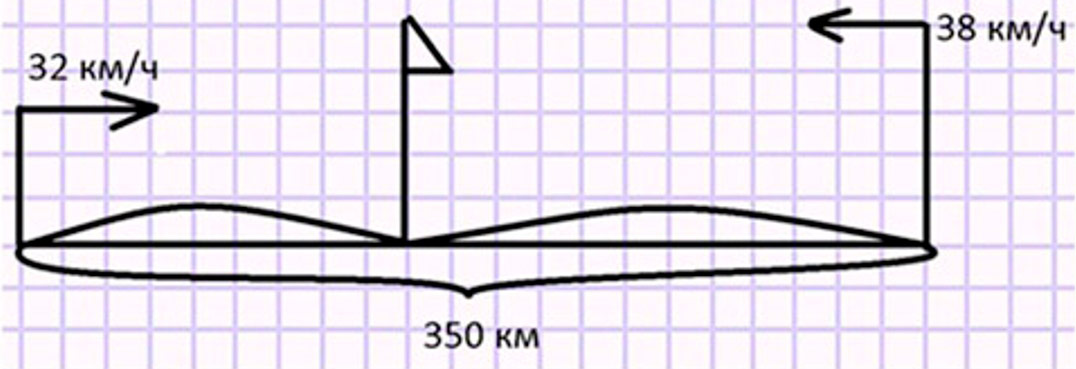
Рассуждаем.
Найдем скорость сближения теплоходов.
1) 32 + 38 = 70 (км/ч) – скорость сближения.
Продолжаем рассуждение.
Узнаем, какое количество времени теплоходы были в пути.
2) 350 : 70 = 5 (ч) – теплоходы были в пути.
Продолжаем рассуждение.
Узнаем, с какое время теплоходы встретятся.
3) 11 + 5 = 16 (ч) – время, когда теплоходы встретятся.
Записываем ответ.
Ответ: в 16 часов.
Номер 23.
Два велосипедиста отправились из одного посёлка одновременно в противоположных направлениях. Через 30 мин расстояние между ними было 15 км. Скорость одного из них 260 м/мин. Узнай скорость другого велосипедиста. (Вырази 15 км в метрах.) Составь и реши задачи, обратные данной.
Ответ:
15 км = 15000 м
1) 260 ∙ 30 = 7800 (м) – проехал один велосипедист.
2) 15000 − 7800 = 7200 (м) – проехал другой велосипедист.
3) 7200 : 30 = 240 (м/мин) – скорость другого велосипедиста.
Ответ: скорость другого велосипедиста составляет 240 м/мин.
Обратная задача 1:
Два велосипедиста одновременно отправились из одного поселка в противоположных направлениях. Средняя скорость одного из них 260 м / мин, а другого – 240 м/ мин. Какое расстояние будет между ними через 30 мин? Вырази расстояние между ними через 30 минут в километрах.
.jpg "Изображение математика 4 класс Моро, Бантова - 2 часть страница 56, номер 23, задача 2")
1) 260 + 240 = 500 (м/мин) – скорость удаления.
2) 500 ∙ 30 = 15000 (м) = 15 км – расстояние между велосипедистами через 30 минут езды.
Ответ: расстояние между велосипедистами через 30 минут составит 15 км.
Обратная задача 2:
Два велосипедиста одновременно отправились из поселка в противоположных направлениях. Скорость одного из них 260 м/мин, а скорость другого 240 м/мин. Через сколько минут расстояние между ними будет 15 км?
.jpg "Изображение математика 4 класс Моро, Бантова - 2 часть страница 56, номер 23, задача 3")
15 км = 15000 м
1) 260 + 240 = 500 (м/мин) – скорость удаления.
2) 15000 : 500 = 30 (мин) – время, через которое расстояние между велосипедистами будет равно 15 км.
Ответ: расстояние между велосипедистами через 30 минут составит 15 км.
Повтори взаимосвязь между скоростью, временем и расстоянием.
Шаг 1.
Рассуждаем и выполняем вычисление.
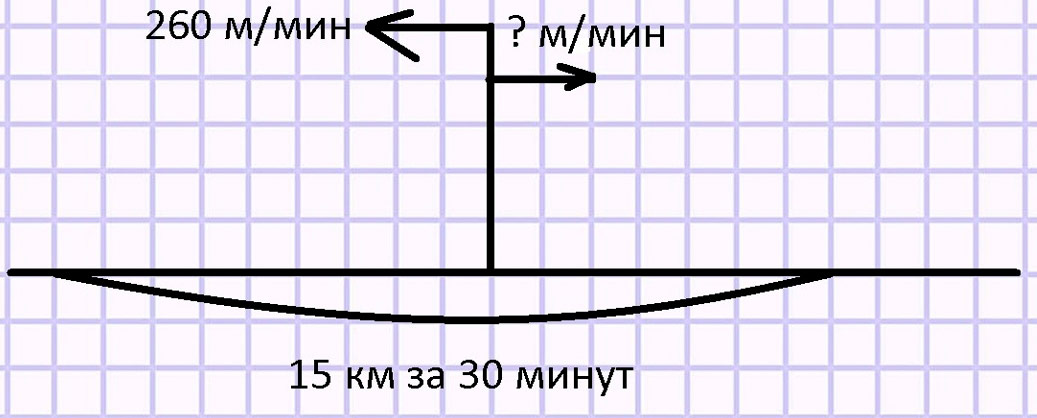
Рассуждаем.
Узнаем, сколько метров проехал один велосипедист.
15 км = 15000 м
1) 260 ∙ 30 = 7800 (м) – проехал один велосипедист.
Продолжаем рассуждение.
Узнаем, сколько метров проехал другой велосипедист.
2) 15000 − 7800 = 7200 (м) – проехал другой велосипедист.
Продолжаем рассуждение.
Узнаем скорость другого велосипедиста. Для этого расстояние, которое он преодолел, разделим на время в пути.
3) 7200 : 30 = 240 (м/мин) – скорость другого велосипедиста.
Записываем ответ.
Ответ: 240 м/мин.
Шаг 1.
Составим первую задачу обратную данной.
Два велосипедиста одновременно отправились из одного поселка в противоположных направлениях. Средняя скорость одного из них 260 м / мин, а другого – 240 м/ мин. Какое расстояние будет между ними через 30 мин? Вырази расстояние между ними через 30 минут в километрах.
Оформляем условие в виде схематического чертежа.
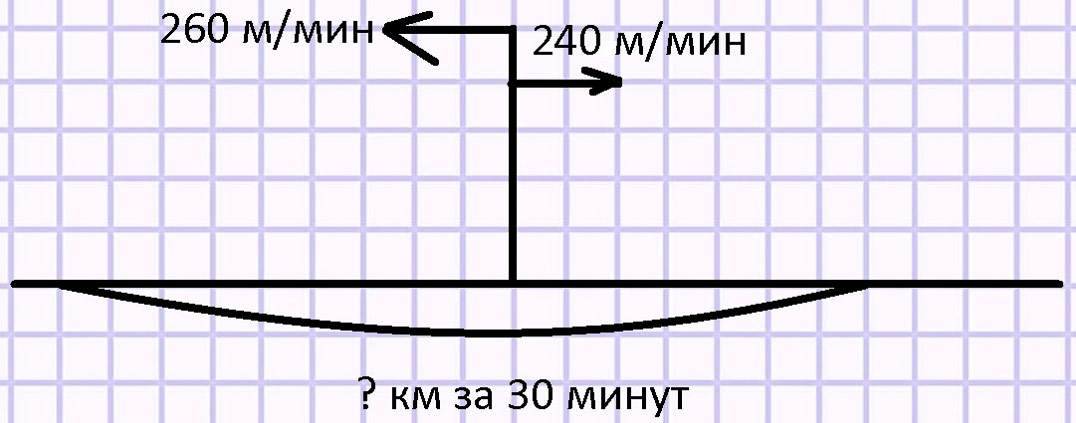
Рассуждаем.
Узнаем скорость удаления велосипедистов.
1) 260 + 240 = 500 (м/мин) – скорость удаления.
Продолжаем рассуждение.
Узнаем расстояние между велосипедистами через 30 минут езды.
2) 500 ∙ 30 = 15000 (м) = 15 км – расстояние между велосипедистами через 30 минут езды.
Записываем ответ.
Ответ: 15 км.
Шаг 1.
Составим вторую задачу обратную данной.
Два велосипедиста одновременно отправились из поселка в противоположных направлениях. Скорость одного из них 260 м/мин, а скорость другого 240 м/мин. Через сколько минут расстояние между ними будет 15 км?
Оформляем условие в виде схематического чертежа.
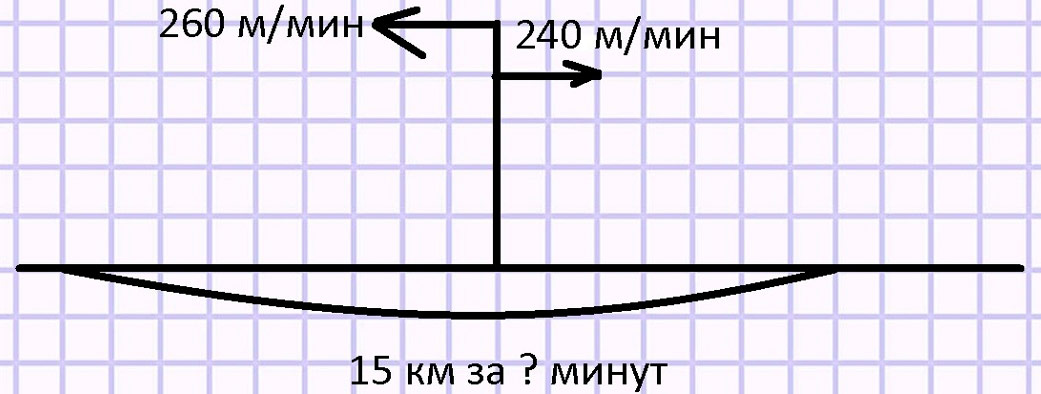
Рассуждаем.
15 км = 15000 м
Узнаем скорость удаления велосипедистов.
1) 260 + 240 = 500 (м/мин) – скорость удаления.
Продолжаем рассуждение.
Узнаем, через какое время расстояние между велосипедистами будет 15 км.
2) 15000 : 500 = 30 (мин) – время, через которое расстояние между велосипедистами будет равно 15 км.
Записываем ответ.
Ответ: через 30 минут.
Номер 24.
В санатории построили бассейн прямоугольной формы, длина которого 15 м, ширина 5 м и глубина 2 м.
1) Сколько квадратных кафельных плиток со стороной 1 дм каждая потребовалось для облицовки дна этого бассейна? стенок этого бассейна?
2) Сколько надо сделать шагов, чтобы обойти весь бассейн, если длина шага 50 см?
Задача 1:
.jpg "Изображение математика 4 класс Моро, Бантова - 2 часть страница 56, номер 24, задача 1")
1 ∙ 1 = 1 (дм²) – площадь одной плитки для облицовки бассейна.
15 ∙ 5 = 75 (м²) – площадь дна бассейна.
75 м² ∙ 100 = 75 (дм²) (умножаем на 100, потому что 1 м² = 100дм²)
7500 ∙ 1 = 7500 (кафельных плиток) – понадобятся для облицовки дна бассейна.
Теперь найдем площади стенок:
1ая стенка: 5 ∙ 2 = 10 (м²)
2ая стенка: 2 ∙ 15 = 30 (м²)
3ья стенка: 2 ∙ 5 = 10 (м²)
4ая стенка: 15 ∙ 2 = 30 (м²)
Мы видим, что стены бассейна попарно равны, то есть в бассейне 4 стороны и две противоположные равны. Поэтому, можно найти площадь всех сторон через выражение:
(2 ∙ 5 + 2 ∙ 15) ∙ 2 = (10 + 30) ∙ 2 = 80 (м²).
80 м² ∙ 100 = 8000 (дм²) (потому что 1 м² = 100дм²)
8000 ∙ 1 = 8000 (кафельных плиток) – понадобятся для облицовки стенок бассейна.
Ответ: 7500 плиток нужно для облицовки бассейна и 8000 плиток необходимо для облицовки стенок бассейна.
Задача 2:
Человеку нужно обойти бассейн, а значит нужно обойти его по бордюру, который имеет форму прямоугольника. Чтобы узнать сколько шагов нужно сделать, нужно прежде всего найти длину всего бордюра, а значит вычислить его периметр.
.jpg "Изображение математика 4 класс Моро, Бантова - 2 часть страница 56, номер 24, задача 2")
(15 + 5) ∙ 2 = 40 (м) – длина бордюра.
40 метров = 4000 см, потому что 1 м = 100 см.
4000 : 50 = 80 (шагов) – нужно сделать, чтобы обойти весь бассейн.
Ответ: 80 шагов всего нужно сделать, чтобы обойти весь бассейн.
Повтори единицы длины – метр и сантиметр, единицы площади, а также как найти площадь и периметр прямоугольника.
Оформляем условие в виде схематического чертежа.
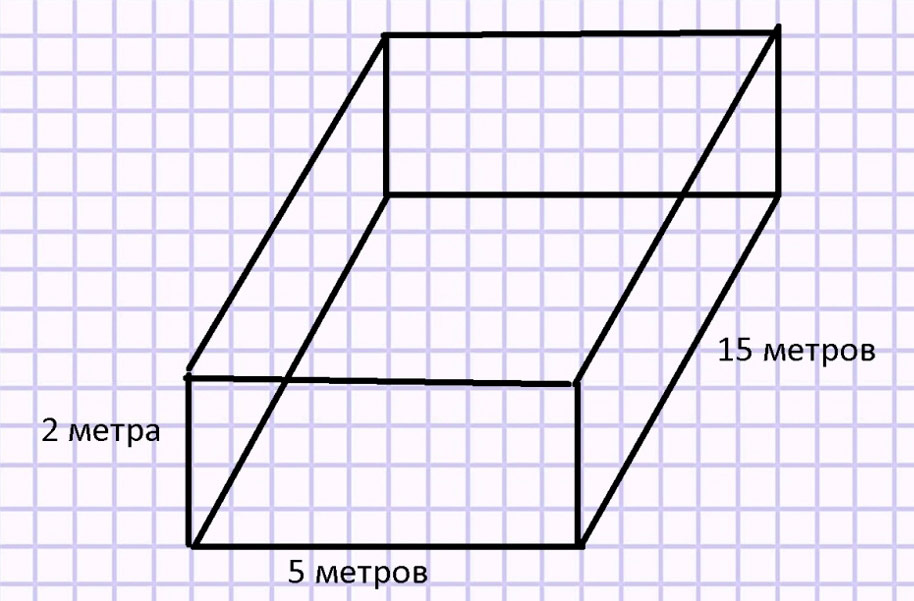
Ответим на первый вопрос задачи.
1 ∙ 1 = 1 (дм²) – площадь одной плитки для облицовки бассейна.
15 ∙ 5 = 75 (м²) – площадь дна бассейна.
75 м² ∙ 100 = 75 (дм²) (умножаем на 100, потому что 1 м² = 100дм²)
7500 ∙ 1 = 7500 (кафельных плиток) – понадобятся для облицовки дна бассейна.
Теперь найдем площади стенок:
1ая стенка: 5 ∙ 2 = 10 (м²)
2ая стенка: 2 ∙ 15 = 30 (м²)
3ья стенка: 2 ∙ 5 = 10 (м²)
4ая стенка: 15 ∙ 2 = 30 (м²)
Мы видим, что стены бассейна попарно равны, то есть в бассейне 4 стороны и две противоположные равны. Поэтому, можно найти площадь всех сторон через уравнение:
(2 ∙ 5 + 2 ∙ 15) ∙ 2 = (10 + 30) ∙ 2 = 80 (м²).
80 м² ∙ 100 = 8000 (дм²) (потому что 1 м² = 100дм²)
8000 ∙ 1 = 8000 (кафельных плиток) – понадобятся для облицовки стенок бассейна.
Ответ: 7500 плиток и 8000.
Ответим на второй вопрос задачи.
Человеку нужно обойти бассейн, а значит нужно обойти его по бордюру, который имеет форму прямоугольника. Чтобы узнать сколько шагов нужно сделать, нужно прежде всего найти длину всего бордюра, а значит посчитать его периметр.
(15 + 5) ∙ 2 = 40 (м) – длина бордюра.
40 метров = 4000 см, потому что 1 м = 100 см.
4000 : 50 = 80 (шагов) – нужно сделать, чтобы обойти весь бассейн.
Ответ: 80 шагов.
Номер 25.
Составь по данной таблице выражения, которые показывают:
1) стоимость всех купленных столов и стульев;
2) на сколько больше стоимость всех стульев, чем стоимость всех столов;
3) стоимость всех столов и шести стульев.
Ответ:
1) а ∙ 8 + к ∙ 36; 2) к ∙ 36 - а ∙ 8; 3) а ∙ 8 + к ∙ 6
Повтори взаимосвязь между ценой, количеством и стоимостью, а также что такое буквенные выражения.
Составим выражения по данным таблицы.
Чтобы найти стоимость, нужно цену умножить на количество.
1) 8 ∙ а + 36 ∙ к;
2) 36 ∙ к − 8 ∙ а;
3) 8 ∙ а + 36 ∙ к.
Оформим задание в тетрадь.
Номер 1.
Объясни на примере, как можно по-разному умножить число на сумму.
Ответ:4 ∙ (5 + 3) = 4 ∙ 8 = 32 4 ∙ (5 + 3) = 4 ∙ 5 + 4 ∙ 3 = 20 + 12 = 32
Повтори, как называются числа при умножении.
Выполняем вычисления.
Чтобы умножить число на сумму, можно сначала выполнить сложение, а затем умножить число на полученный результат.
4 ∙ (5 + 3) = 4 ∙ 8 = 32
Для умножения числа на сумму, можно умножить данное число на каждое слагаемое отдельно и полученные результаты сложить.
4 ∙ (5 + 3) = 4 ∙ 5 + 4 ∙ 3 = 20 + 12 = 32
Оформляем задание в тетрадь.
4 ∙ (5 + 3) = 4 ∙ 8 = 32
4 ∙ (5 + 3) = 4 ∙ 5 + 4 ∙ 3 = 20 + 12 = 32
Номер 2.
Составь примеры на умножение двузначного числа на двузначное и трёхзначного числа на трёхзначное. Реши их с объяснением.
Ответ:1) 12 ∙ 37
Умножу первый множитель на число единиц:
12 ∙ 5 = 60
Получу первое неполное произведение 60.
Умножу первый множитель на число десятков:
12 ∙ 3 = 36
Начну записывать первое неполное произведение под единицами, а второе под десятками.
Сложу неполные произведения.
Читаю ответ: произведение чисел 12 и 35 равно 420.
2) 123 ∙ 937
.jpg "Изображение математика 4 класс Моро, Бантова - 2 часть страница 56, номер 2, пример 2")
Умножу первый множитель на число единиц: 123 ∙ 7 = 861 Получу первое неполное произведение 861. Умножу первый множитель на число десятков: 123 ∙ 8 = 984 Получу второе неполное произведение: 984. Умножу первый множитель на число сотен: 123 ∙ 9 = 1107 Начну подписывать первое неполное произведение под единицами,а второе неполное произведение под десятками. Третье неполное произведение записываю под сотнями. Сложу неполные произведения. Читаю ответ: произведение чисел 123 и 789 равно 121401.
Повтори алгоритм письменного умножения на двузначные и трёхзначные числа.
Выполняем вычисления.
1) 12 ∙ 37
Умножу первый множитель на число единиц:
12 ∙ 5 = 60
Получу первое неполное произведение 60.
Умножу первый множитель на число десятков:
12 ∙ 3 = 36
Начну записывать первое неполное произведение под единицами, а второе под десятками.
Сложу неполные произведения.
Читаю ответ: произведение чисел 12 и 35 равно 420.
2) 254 ∙ 937
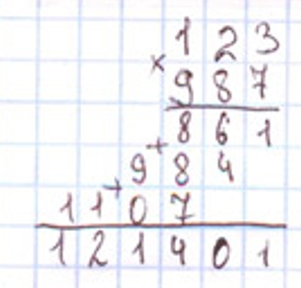
Умножу первый множитель на число единиц:
123 ∙ 7 = 861
Получу первое неполное произведение 861.
Умножу первый множитель на число десятков:
123 ∙ 8 = 984
Получу второе неполное произведение: 984.
Умножу первый множитель на число сотен:
123 ∙ 9 = 1107
Начну подписывать первое неполное произведение под единицами, а второе неполное произведение под десятками. Третье неполное произведение записываю под сотнями.
Сложу неполные произведения.
Читаю ответ: произведение чисел 123 и 789 равно 121401.
Оформляем задание в тетрадь.
Задание на полях страницы
Начерти такой узор.
Ответ:
1. Нарисуй в ряд по вертикали 4 кружка, диаметр каждого из которых 2 см. 2. Внутри каждого нарисуй ромб так, чтобы они соприкасались кончиками и образовывали гирлянду сверху вниз. Длина ромба 2 см, а ширина 1 см. 3. В точке, где мысленно проведенная длина и ширина пересекаются поставь точку - это начало другой цепочки из ромбов уже другого цвета. Строй их также как и предыдущую цепочку (ширина 1 см, а длина - 2 см. 4. Сверху и снизу дорисуй перекладинки ромба, чтобы они касались круга.
Повтори, что такое окружность, а также какие бывают многоугольники.
Рассмотрим данный узор.
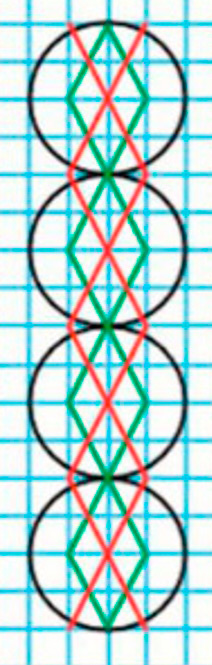
Начертим узор в тетрадь.
1. Нарисуй в ряд по вертикали 4 кружка, диаметр каждого из которых 2 см.
2. Внутри каждого нарисуй ромб так, чтобы они соприкасались кончиками и образовывали гирлянду сверху вниз. Длина ромба 2 см, а ширина 1 см.
3. В точке, где мысленно проведенная длина и ширина пересекаются поставь точку – это начало другой цепочки из ромбов уже другого цвета. Строй их также как и предыдущую цепочку (ширина 1 см, а длина – 2 см.
4. Сверху и снизу дорисуй перекладинки ромба, чтобы они касались круга.
Что узнали. Чему научились
Номер 1.
Проверь, верны ли равенства.
Ответ:
13 ∙ (10 + 2) = 13 ∙ 10 + 13 ∙ 2 – верно.
15 ∙ (10 ∙ 2) = 15 ∙ 10 ∙ 2 – верно.
(20 + 5) ∙ 4 = 20 + 5 ∙ 4 – неверно, потому что (20 + 5) ∙ 4 = 20 ∙ 4 + 5 ∙ 4.
72 : (8 ∙ 2) = 72 : 8 ∙ 3 – неверно, потому что 72 : (8 ∙ 2) = 72 : 8 : 2.
Повтори свойства умножения.
Рассуждаем.
13 ∙ (10 + 2) = 13 ∙ 10 + 13 ∙ 2 – верное равенство.
Так как в данном выражении используется распределительное свойство:
При умножении числа на сумму можно умножить его на каждое слагаемое в отдельности и полученные результаты сложить.
Проверим вычислением.
13 ∙ (10 + 2) = 13 ∙ 12 = 156
13 ∙ 10 + 13 ∙ 2 = 130 + 26 = 156
156 = 156
15 ∙ (10 ∙ 2) = 15 ∙ 10 ∙ 2 – верное равенство.
Так как в данном выражении используется сочетательное свойство:
При умножении числа на произведение можно сначала умножить число на один множитель, а полученный результат умножить на другой множитель.
Проверим вычислением.
15 ∙ (10 ∙ 2) = 15 ∙ 20 = 300
15 ∙ 10 ∙ 2 = 150 ∙ 2 = 300
300 = 300
(20 + 5) ∙ 4 = 20 + 5 ∙ 4 – неверное равенство.
Так как в данном выражении не работает распределительное свойство:
При умножении числа на сумму можно умножить его на каждое слагаемое в отдельности и полученные результаты сложить.
Проверим вычислением.
(20 + 5) ∙ 4 = 25 ∙ 4 = 100
20 + 5 ∙ 4 = 20 + 20 = 40
100 ≠ 40
72 : (8 ∙ 3) = 72 : 8 ∙ 3 – неверное равенство.
Так как в данном выражении используется сочетательное свойство:
При умножении числа на произведение можно сначала умножить число на один множитель, а полученный результат умножить на другой множитель.
Проверим вычислением.
72 : (8 ∙ 3) = 72 : 24 = 3
72 : 8 ∙ 3 = 9 ∙ 3 = 27
3 ≠ 24
Оформим задание в тетрадь.
13 ∙ (10 + 2) = 13 ∙ 10 + 13 ∙ 2 – верно
15 ∙ (10 ∙ 2) = 15 ∙ 10 ∙ 2 – верно
(20 + 5) ∙ 4 = 20 + 5 ∙ 4 – неверно,
потому что (20 + 5) ∙ 4 = 20 ∙ 4 + 5 ∙ 4
72 : (8 ∙ 2) = 72 : 8 ∙ 3 – неверно,
потому что 72 : (8 ∙ 2) = 72 : 8 : 2
Номер 2.
Ответ:
Повтори алгоритм письменного сложения и умножения трёхзначных чисел, а также порядок действий.
Выполняем вычисления.
Выполним вычисление по действиям.
(990 – 90) : 100 ∙ 9 = 81
В данном выражении сначала выполняется действие в скобках – вычитание, затем действия вне скобок – деление, а потом – умножение.
1) 990 – 90 = 900 + 90 – 90 = 900
2) 900 : 100 = 9
3) 9 ∙ 9 = 81
990 – 40 + 25 ∙ 7 ∙ 4 = 1650
В данном выражении сначала выполняются действия умножения по порядку, затем вычитание, а потом – сложение.
1) 25 ∙ 7 = (20 + 5) ∙ 7 = 140 + 35 = 175
2) 175 ∙ 4 = (100 + 70 + 5) ∙ 4 = 400 + 280 + 20 = 700
3) 990 – 40 = 900 + 90 – 40 = 900 + 50 = 950
4) 950 + 700 = 1650
1000 : (1000 ∙ 1) – 1 = 0
В данном выражении сначала выполняется действие в скобках – умножение, затем действия вне скобок – деление, а потом – вычитание.
1) 1000 ∙ 1 = 1000
2) 1000 : 1000 = 1
3) 1 – 1 = 0
12 ∙ 5 + (84 – 72 : 3) = 120
В данном выражении сначала выполняется действие в скобках – деление, после чего – вычитание, затем действия вне скобок – умножение, а потом – сложение.
1) 72 : 3 = (60 + 12) : 3 = 20 + 4 = 24
2) 84 – 24 = 80 + 4 – 20 – 4 = 80 – 20 = 60
3) 12 ∙ 5 = (10 + 2) ∙ 5 = 50 + 10 = 60
4) 60 + 60 = 120
Оформляем задание в тетрадь.
Номер 3.
Найди значения выражений a + b и a − b, если: 1) a = 30100 и b = 20935; 2) a = 28005 и b = 13706.
Ответ:1)
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 56, номер 3, пример 1, 2024 год.")
2)
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 56, номер 3, пример 2, 2024 год.")
Повтори, что такое буквенные выражения.
Вычисляем.
Чтобы найти значение буквенного выражения, нужно в это выражение вместо букв подставить данные числа и выполнить вычисления.
Если a = 30100 и b = 20935, то
a + b = 30100 + 20935 = 51035
a – b = 30100 – 20935 = 9165
Продолжаем вычисления.
Чтобы найти значение буквенного выражения, нужно в это выражение вместо букв подставить данные числа и выполнить вычисления.
Если a = 28005 и b = 13706, то
a + b = 28005 + 13706 = 41711
a – b = 28005 – 13706 = 14299
Оформляем задание в тетрадь.
1)
2)
Номер 4.
Найди значения выражений с ∙ d и с : d, если c = 6030 и d = 90.
Ответ:
Повтори, что такое буквенные выражения.
Выполняем вычисления.
Чтобы найти значение буквенного выражения, нужно в это выражение вместо букв подставить данные числа и выполнить вычисления.
Если c = 6030 и d = 90, то
c ∙ d = 6030 ∙ 90 = 542700
c : d = 6030 : 90 = 603 : 9 = 67
Оформляем задание в тетрадь.
Номер 5.
Вычисли удобным способом.
Ответ:
87 ∙ 64 + 87 ∙ 36 = 87 ∙ (64 + 36) = 87 ∙ 100 = 8700
39 ∙ 16 + 39 ∙ 4 = 39 ∙ (16 + 4) = 39 ∙ 20 = 780
96 ∙ 77 − 96 ∙ 76 = 96 ∙ (77 − 76) = 96 ∙ 1 = 96
48 ∙ 61 − 40 ∙ 61 = 61 ∙ (48 − 40) = 61 ∙ 8 = 488
24 ∙ 49 + 24 = 24 ∙ 49 + 24 ∙ 1 = 24 ∙ (49 + 1) = 24 ∙ 50 = 1200
34 ∙ 21 − 34 = 34 ∙ 21 − 34 ∙ 1 = 34 ∙ (21 − 1) = 34 ∙ 20 = 680
Повтори свойства умножения.
Выполняем вычисления.
87 ∙ 64 + 87 ∙ 36 = 87 ∙ (64 + 36) = 87 ∙ 100 = 8700
Воспользуемся распределительным свойством сложения.
Чтобы умножить число на сумму, можно это число умножить на каждое слагаемое и полученные результаты сложить.
39 ∙ 16 + 39 ∙ 4 = 39 ∙ (16 + 4) = 39 ∙ 20 = 780
Воспользуемся распределительным свойством сложения.
Чтобы умножить число на сумму, можно это число умножить на каждое слагаемое и полученные результаты сложить.
96 ∙ 77 − 96 ∙ 76 = 96 ∙ (77 − 76) = 96 ∙ 1 = 96
Воспользуемся распределительным свойством вычитания.
Чтобы умножить число на разность, можно это число умножить на уменьшаемое и вычитаемое, и из первого полученного результата вычесть второй.
48 ∙ 61 − 40 ∙ 61 = 61 ∙ (48 − 40) = 61 ∙ 8 = 488
Воспользуемся распределительным свойством вычитания.
Чтобы умножить число на разность, можно это число умножить на уменьшаемое и вычитаемое, и из первого полученного результата вычесть второй.
24 ∙ 49 + 24 = 24 ∙ 49 + 24 ∙ 1 = 24 ∙ (49 + 1) = 24 ∙ 50 = 1200
Воспользуемся распределительным свойством сложения.
Чтобы умножить число на сумму, можно это число умножить на каждое слагаемое и полученные результаты сложить.
34 ∙ 21 − 34 = 34 ∙ 21 − 34 ∙ 1 = 34 ∙ (21 − 1) = 34 ∙ 20 = 680
Воспользуемся распределительным свойством вычитания.
Чтобы умножить число на разность, можно это число умножить на уменьшаемое и вычитаемое, и из первого полученного результата вычесть второй.
Оформляем задание в тетрадь.
87 ∙ 64 + 87 ∙ 36 = 87 ∙ (64 + 36) = 87 ∙ 100 = 8700
39 ∙ 16 + 39 ∙ 4 = 39 ∙ (16 + 4) = 39 ∙ 20 = 780
96 ∙ 77 − 96 ∙ 76 = 96 ∙ (77 − 76) = 96 ∙ 1 = 96
48 ∙ 61 − 40 ∙ 61 = 61 ∙ (48 − 40) = 61 ∙ 8 = 488
24 ∙ 49 + 24 = 24 ∙ 49 + 24 ∙ 1 = 24 ∙ (49 + 1) = 24 ∙ 50 = 1200
34 ∙ 21 − 34 = 34 ∙ 21 − 34 ∙ 1 = 34 ∙ (21 − 1) = 34 ∙ 20 = 680
Номер 6.
Запиши неравенства и проверь, верны ли они.
1) Частное чисел 36150 и 50 меньше разности чисел 2010 и 1285.
2) Произведение чисел 701 и 322 больше, чем 200000.
Повтори, как называются числа при вычитании, умножении и делении, а также что такое неравенства.
Записываем неравенства.
36150 : 50 < 2010 – 1285
701 ∙ 322 > 200000
Выполняем вычисления.
36150 : 50 < 2010 – 1285
1) 36150 : 50 = 723
2) 2010 – 1285 = 725
723 < 725 – верно.
Значит, неравенство 36150 : 50 < 2010 – 1285 – верно.
701 ∙ 322 > 200000
701 ∙ 322 = 225722
225722 > 200000 – верно.
Значит, неравенство 701 ∙ 322 > 200000 – верно.
Оформляем задание в тетрадь.
Номер 7.
Ответ:
Повтори алгоритм умножения на трёхзначные числа.
Выполняем вычисления.
702 ∙ 144 = 101088
702 ∙ 4 = 2808 – первое неполное произведение.
702 ∙ 4 = 2808 – второе неполное произведение.
702 ∙ 1 = 702 – третье неполное произведение.
Складываем неполные множители.
Произведение чисел 702 и 144 равно 101088.
320 ∙ 588 = 188160
32 ∙ 8 = 256 – первое неполное произведение.
32 ∙ 8 = 256 – второе неполное произведение.
32 ∙ 5 = 160 – третье неполное произведение.
Складываем неполные множители и приписываем справа один нуль.
Произведение чисел 320 и 588 равно 188160.
705 ∙ 206 = 145230
705 ∙ 6 = 4230 – первое неполное произведение.
Второе неполное произведение равно 0.
705 ∙ 2 = 1410 – третье неполное произведение.
Складываем неполные множители.
Произведение чисел 705 и 206 равно 145230.
802 ∙ 103 = 82606
802 ∙ 3 = 2406 – первое неполное произведение.
Второе неполное произведение равно 0.
802 ∙ 1 = 802 – третье неполное произведение.
Складываем неполные множители.
Произведение чисел 802 и 103 равно 82606.
237 ∙ 405 = 95985
237 ∙ 5 = 1185 – первое неполное произведение.
Второе неполное произведение равно 0.
237 ∙ 4 = 948 – третье неполное произведение.
Складываем неполные множители.
Произведение чисел 237 и 405 равно 95985.
194 ∙ 308 = 59752
194 ∙ 8 = 1552 – первое неполное произведение.
Второе неполное произведение равно 0.
197 ∙ 3 = 582 – третье неполное произведение.
Складываем неполные множители.
Произведение чисел 197 и 308 равно 59752.
490 ∙ 360 = 176400
49 ∙ 6 = 294 – первое неполное произведение.
49 ∙ 3 = 147 – второе неполное произведение.
Складываем неполные множители и приписываем справа два нуля.
Произведение чисел 490 и 360 равно 176400.
670 ∙ 280 = 187600
67 ∙ 8 = 536 – первое неполное произведение.
67 ∙ 2 = 134 – второе неполное произведение.
Складываем неполные множители и приписываем справа два нуля.
Произведение чисел 670 и 280 равно 187600.
Оформляем задание в тетрадь.
Номер 8.
Ответ:
Повтори алгоритм письменного сложения, вычитания, умножения и деления на трёхзначное число, а также порядок действий.
Рассуждаем и выполняем вычисление.
720 ∙ 400 – 195046 = 92954
В данном выражении сначала выполняется действие умножение, а затем – вычитание.
1) 720 ∙ 400 = 288000
2) 288000 – 195046 = 92954
83249 + 6710 ∙ 80 = 620049
В данном выражении сначала выполняется действие умножение, а затем – сложение.
1) 6710 ∙ 80 = 536800
2) 83249 + 536800 = 620049
264037 + 516600 : 900 – 17080 = 247531
В данном выражении сначала выполняется действие деление, затем – сложение, а потом – вычитание.
1) 516600 : 900 = 574
2) 264037 + 574 = 264611
3) 264611 – 17080 = 247531
450430 – 196000 : 700 + 98764 = 548914
В данном выражении сначала выполняется действие деление, затем – вычитание, а потом – сложение.
1) 196000 : 700 = 280
2) 450430 – 280 = 450150
3) 450150 + 98764 = 548914
Оформляем задание в тетрадь.
Номер 9.
Выполни деление с остатком и проверь решение.
Ответ:
Повтори, как выполняется деление с остатком.
Выполняем вычисления.
387 : 50 = 7 (ост. 37)
Проверка:
1) 37 < 50
2) 7 ∙ 50 + 37 = 350 + 37 = 387
5893 : 70 = 84 (ост. 13)
Проверка:
1) 13 < 70
2) 84 ∙ 70 + 13 = (80 + 4) ∙ 70 + 13 = 5600 + 280 + 13 = 5893
764 : 200 = 3 (ост. 164)
Проверка:
1) 164 < 200
2) 3 ∙ 200 + 164 = 600 + 164 = 764
9361 : 600 = 15 (ост. 361)
Проверка:
1) 361 < 600
2) 15 ∙ 600 + 361 = 9000 + 361 = 9361
Оформляем задание в тетрадь.
Номер 10.
Используя эти выражения, составь верные равенства.
Ответ:
32 ∙ 40 + 32 ∙ 6 = 32 ∙ 46
23 ∙ 50 + 23 ∙ 4 = 23 ∙ 54
46 ∙ 30 + 46 ∙ 2 = 46 ∙ 32
54 ∙ 20 + 54 ∙ 3 = 54 ∙ 23
32 ∙ 40 + 32 ∙ 6 = 46 ∙ 30 + 46 ∙ 2
23 ∙ 50 + 23 ∙ 4 = 54 ∙ 20 + 54 ∙ 3
23 ∙ 54 = 54 ∙ 23
32 ∙ 46 = 46 ∙ 32
Повтори, что такое равенства.
Выполняем вычисления.
Чтобы умножить число на сумму, можно умножить это число на каждое слагаемое и сложить полученные результаты.
32 ∙ 40 + 32 ∙ 6 = 32 ∙ (40 + 6) = 32 ∙ 46
23 ∙ 50 + 23 ∙ 4 = 23 ∙ (50 + 4) = 23 ∙ 54
46 ∙ 30 + 46 ∙ 2 = 46 ∙ (30 + 2) = 46 ∙ 32
54 ∙ 20 + 54 ∙ 3 = 54 ∙ (20 + 3) = 54 ∙ 23
Оформляем задание в тетрадь.
32 ∙ 40 + 32 ∙ 6 = 32 ∙ 46
32 ∙ 40 + 32 ∙ 6 = 46 ∙ 32
23 ∙ 50 + 23 ∙ 4 = 23 ∙ 54
23 ∙ 50 + 23 ∙ 4 = 54 ∙ 23
46 ∙ 30 + 46 ∙ 2 = 46 ∙ 32
46 ∙ 30 + 46 ∙ 2 = 32 ∙ 46
54 ∙ 20 + 54 ∙ 3 = 54 ∙ 23
54 ∙ 20 + 54 ∙ 3 = 23 ∙ 54
32 ∙ 40 + 32 ∙ 6 = 46 ∙ 30 + 46 ∙ 2
23 ∙ 50 + 23 ∙ 4 = 54 ∙ 20 + 54 ∙ 3
23 ∙ 54 = 54 ∙ 23
32 ∙ 46 = 46 ∙ 32
Номер 11.
Составь по задачам уравнения и реши их.
1) Какое число надо умножить на 4, чтобы получить разность чисел 350 и 70?
2) На какое число надо разделить 750, чтобы получить сумму чисел 32 и 18?
1) х ∙ 4 = 350 − 70
х ∙ 4 = 280
х = 280 : 4
x = 70
70 ∙ 4 = 350 − 70
280 = 280
Ответ: х = 70.
2) 750 : х = 32 + 18
750 : х = 50
х = 750 : 50
x = 15
750 : 15 = 32 + 18
50 = 50
Ответ: х = 15.
Повтори, как решать уравнения.
Выполняем вычисления.
В каждом из составленных уравнений сначала выполняем вычисления в правой части.
1) 4 ∙ х = 350 – 70
4 ∙ х = 280
Чтобы найти первый множитель, нужно произведение разделить на второй множитель:
х = 280 : 4
х = 70
Проверка:
4 ∙ 70 = 350 – 70
280 = 280
2) 750 : х = 32 + 18
750 : х = 50
Чтобы найти делитель, нужно делимое разделить на частное:
х = 750 : 50
х = 15
Проверка:
750 : 15 = 32 + 18
50 = 50
Оформляем задание в тетрадь.
1) 4 ∙ х = 350 – 70
4 ∙ х = 280
х = 280 : 4
х = 70
Проверка:
4 ∙ 70 = 350 – 70
280 = 280
Ответ: х = 70.
2) 750 : х = 32 + 18
750 : х = 50
х = 750 : 50
х = 15
Проверка:
750 : 15 = 32 + 18
50 = 50
Ответ: х = 15.
Номер 12.
Сравни скорости, с которыми могут двигаться разные животные (с. 80 – 81).
Ответ:Переведем все представленные скорости в одной единице измерения (км/ч). Расстояние необходимо привести к единице км, а время – к часам.
Тогда табличка скоростей выглядит так:
Теперь сравним скорости животных.
А) По убыванию (начиная с самого быстрого):
1) стриж 120 км/ч;
2) гепард 108 км/ч;
3) антилопа 90 км/ч;
4) голубь 60 – 90 км/ч;
5) лев 80 км/ч;
6) зебра 60 км/ч;
7) воробей 30-60 км/ч;
8) жираф 45 км/ч;
9) аист 36 км/ч;
10) страус 30 км/ч.
Б) По возрастанию (начиная с самого медленного):
1) страус 30 км/ч;
2) аист 36 км/ч;
3) жираф 45 км/ч;
4) воробей 30 – 60 км/ч;
5) зебра 60 км/ч;
6) лев 80 км/ч;
7) голубь 60 – 90 км/ч;
8) антилопа 90 км/ч;
9) гепард 108 км/ч;
10) стриж 120 км/ч.
Повтори, в каких единицах измеряется скорость.
Рассуждаем.
Переведем все представленные скорости в одной единице измерения (км/ч).
Расстояние необходимо привести к единице км, а время – к часам.
Тогда табличка скоростей выглядит так:
Продолжаем рассуждения.
Сравним скорости животных.
А) По убыванию (начиная с самого быстрого):
1) стриж 120 км/ч;
2) гепард 108 км/ч;
3) антилопа 90 км/ч;
4) голубь 60-90 км/ч;
5) лев 80 км/ч;
6) зебра 60 км/ч;
7) воробей 30-60 км/ч;
8) жираф 45 км/ч;
9) аист 36 км/ч;
10) страус 30 км/ч.
Б) По возрастанию (начиная с самого медленного):
1) страус 30 км/ч;
2) аист 36 км/ч;
3) жираф 45 км/ч;
4) воробей 30-60 км/ч;
5) зебра 60 км/ч;
6) лев 80 км/ч;
7) голубь 60-90 км/ч;
8) антилопа 90 км/ч;
9) гепард 108 км/ч;
10) стриж 120 км/ч.
Задание на полях страницы
Занимательная рамка.
Ответ:
Проверка:
80 + 120 + 50 = 200 + 50 = 250
80 + 140 + 30 = 110 + 140 = 250
30 + 210 + 10 = 210 + 40 = 250
50 + 190 + 10 = 50 + 200 = 250
В занимательных рамках сумма всех чисел на каждой стороне должна равняться числу в центре.
Рассмотрим рисунок.
Сумма в строках и столбцах равна 250.
Выполним вычисления.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известные слагаемые.
250 – (50 + 10) = 250 – 60 = 190
250 – (80 + 50) = 250 – 130 = 120
250 – (30 + 10) = 250 – 40 = 210
250 – (80 + 30) = 250 – 110 = 140
Оформим задание в тетрадь.
Ребус.
-1.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 56, задание на полях страницы, ребус. 2024 год.")
Ответ:
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 56, задание на полях страницы, ребус. 2024 год.")
Перед нами ребус, для того чтобы найти недостающие цифры необходимо выполнить деление.
Рассмотрим ребус.
Рассуждаем.
Какое двузначное число с цифрой 6 в единицах делится на однозначное число без остатка и в частном получается 9? Это число 36.
Значит, делитель – число 4, так как 36 : 9 = 4.
Далее делили однозначное число, смогли поделить 8 единиц и в остатке получилось 1. Значит, делили число 9.
9 : 4 = 2 (ост. 1)
Какое двузначное число разделили на 4 и получили 2 в остатке? Это число 8. 8 : 4 = 2.
Оформим задание в тетрадь.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽
Напишите свой комментарий.