Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 49

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Задание вверху страницы
Рассмотри и сравни, как выполнено умножение.
Назови каждое неполное произведение.
Объясни, почему в таких случаях при умножении на трехзначное число записывают только два неполных произведения и как их подписывают.

Умножение трехзначного числа на трехзначное с нулем на месте десятков выполняют следующим образом: умножают первый множитель на количество единиц, умножение на количество десятков пропускается, потому что второе произведение равно 0, а третье произведение записывают под сотнями. Два неполных произведения (по сути три, но второе равно 0) складывают и записывают ответ. Умножение трехзначного числа на трехзначное число с нулем на конце выполняют немного по-другому. Второй множитель с нулем на конце записывают со сдвигом влево на 1 знак, так что нуль не участвует в умножении. Это делается для того, чтобы сократить лишнюю работу и не записывать целую строку нулей, как результат умножения первого множителя на количество единиц. Далее выполняются умножения на количество десятков, сотен, результаты записываются со сдвигом влево и затем складываются, а нуль на конце приписывают. Проще говоря, при умножении трехзначного числа на трехзначное число с нулем на конце пропускается действие умножение первого множителя на количество единиц, потому что количество единиц в таком числе равно нулю.
При умножении 327 на 406 получаются три неполных произведения:1962, 0 и 1308. При умножении 614 на 280 получаются три неполных произведения: 4912, 0 и 1228. Но для того, чтобы сократить работу первое неполное произведение не прописывают и не ищут его, так как нуль сдвинут и не участвует в умножении.
При умножении трехзначного числа на трехзначное число с нулем на позиции десятков, получается три неполных произведения. Первое записывается под единицами, второе не записывается, но мысленно мы помним, что оно записывается под десятками, а третье неполное произведение записываем под сотнями. Складываем неполные произведения и читаем ответ. Также есть особенность при умножении трехзначного числа на трехзначное число с нулем на позиции единиц. Второй множитель записывают со сдвигом влево на 1 знак и поэтому число, означающее десятки становится условно единицами, а сотни - десятками. У нас получаются всего два неполных произведения, потому что умножение на нуль не выполняют и первым неполным произведением, записываемым под единицами, становится уже число, полученное при умножении первого множителя на количество десятков. При умножении на количество сотен записывают результат под десятками.
Повтори алгоритм письменного умножения на двузначное и трёхзначное числа.
Рассмотрим данные примеры и их решения.

Рассуждаем, как выполнено вычисление первого примера.
• Умножение трехзначного числа на трехзначное с нулем на месте десятков выполняют следующим образом: умножают первый множитель на количество единиц, умножение на количество десятков пропускается, потому что второе произведение равно 0, а третье произведение записывают под сотнями. Два неполных произведения (по сути три, но второе равно 0) складывают и записывают ответ.
• При умножении 327 на 406 получаются три неполных произведения:1962, 0 и 1308.
• При умножении трехзначного числа на трехзначное число с нулем на позиции десятков, получается три неполных произведения. Первое записывается под единицами, второе не записывается, но мысленно мы помним, что оно записывается под десятками, а третье неполное произведение записываем под сотнями. Складываем неполные произведения и читаем ответ.
Рассуждаем, как выполнено вычисление второго примера.
• Умножение трехзначного числа на трехзначное число с нулем на конце выполняют немного по-другому. Второй множитель с нулем на конце записывают со сдвигом влево на 1 знак, так что нуль не участвует в умножении. Это делается для того, чтобы сократить лишнюю работу и не записывать целую строку нулей, как результат умножения первого множителя на количество единиц. Далее выполняются умножения на количество десятков, сотен, результаты записываются со сдвигом влево и затем складываются, а нуль на конце приписывают. Проще говоря, при умножении трехзначного числа на трехзначное число с нулем на конце пропускается действие умножение первого множителя на количество единиц, потому что количество единиц в таком числе равно нулю.
• При умножении 614 на 280 получаются три неполных произведения: 4912, 0 и 1228. Но для того, чтобы сократить работу первое неполное произведение не прописывают и не ищут его, так как нуль сдвинут и не участвует в умножении.
• Также есть особенность при умножении трехзначного числа на трехзначное число с нулем на позиции единиц. Второй множитель записывают со сдвигом влево на 1 знак и поэтому число, означающее десятки становится условно единицами, а сотни – десятками. У нас получаются всего два неполных произведения, потому что умножение на нуль не выполняют и первым неполным произведением, записываемым под единицами, становится уже число, полученное при умножении первого множителя на количество десятков. При умножении на количество сотен записывают результат под десятками.
Номер 185.
Вычисли с объяснением.
Ответ:
1) 254 ∙ 37
Умножу первый множитель на число единиц:
254 ∙ 7 = 1778
Получу первое неполное произведение 1778.
Умножу первый множитель на число десятков:
254 ∙ 3 = 762
Получу второе неполное произведение: 762.
Начну подписывать второе неполное произведение под десятками.
Сложу неполные произведения.
Читаю ответ: произведение чисел 254 и 37 равно 9398.
2) 254 ∙ 307
Умножу первый множитель на число единиц:
254 ∙ 7 = 1778
Получу первое неполное произведение 1778.
Умножу первый множитель на число десятков:
254 ∙ 0 = 0
Получу второе неполное произведение: 0.
Умножу первый множитель на число сотен:
254 ∙ 3 = 762
Получу третье неполное произведение: 762.
Начну подписывать второе неполное произведение под десятками, а третье под сотнями.
Сложу неполные произведения.
Читаю ответ: произведение чисел 254 и 307 равно 77978.
3) 481 ∙ 360
Записываем второй множитель со сдвигом вправо на 1 знак и таким образом первым действием выполняем умножение первого множителя на количество десятков.
Умножу первый множитель на число десятков:
481 ∙ 6 = 2886
Получу первое неполное произведение 2886.
Умножу первый множитель на число сотен:
481 ∙ 3 = 1443
Получу второе неполное произведение: 1443.
Начну подписывать первое неполное произведение под единицами, а второе неполное произведение под сотнями. Нуль припысываю к ответу справа.
Сложу неполные произведения.
Читаю ответ: произведение чисел 481 и 306 равно 173160.
Повтори алгоритм умножения на двузначные и трёхзначные числа.
Выполняем вычисления.

Объясняем, как выполнено вычисление первого примера.
254 ∙ 37
Умножу первый множитель на число единиц:
254 ∙ 7 = 1778
Получу первое неполное произведение 1778.
Умножу первый множитель на число десятков:
254 ∙ 3 = 762
Получу второе неполное произведение: 762.
Начну подписывать второе неполное произведение под десятками.
Сложу неполные произведения.
Читаю ответ: произведение чисел 254 и 37 равно 9398.
Объясняем, как выполнено вычисление второго примера.
254 ∙ 307
Умножу первый множитель на число единиц:
254 ∙ 7 = 1778
Получу первое неполное произведение 1778.
Умножу первый множитель на число десятков:
254 ∙ 0 = 0
Получу второе неполное произведение: 0.
Умножу первый множитель на число сотен:
254 ∙ 3 = 762
Получу третье неполное произведение: 762.
Начну подписывать второе неполное произведение под десятками, а третье под сотнями.
Сложу неполные произведения.
Читаю ответ: произведение чисел 254 и 307 равно 77978.
Объясняем, как выполнено вычисление третьего примера.
481 ∙ 360
Записываем второй множитель со сдвигом вправо на 1 знак и таким образом первым действием выполняем умножение первого множителя на количество десятков.
Умножу первый множитель на число десятков:
481 ∙ 6 = 2886
Получу первое неполное произведение 2886.
Умножу первый множитель на число сотен:
481 ∙ 3 = 1443
Получу второе неполное произведение: 1443.
Начну подписывать первое неполное произведение под единицами, а второе неполное произведение под сотнями. Нуль приписываю к ответу справа.
Сложу неполные произведения.
Читаю ответ: произведение чисел 481 и 306 равно 173160.
Оформляем задание в тетрадь.
Номер 186.
Ответ:

Повторите алгоритм письменного умножения на многозначное число, сложения и деления на двузначное число, а также порядок действий.
Выполняем вычисления с пояснениями.
Пишу: 456 ∙ 803.
Умножу первый множитель на число единиц:
456 ∙ 3 = 1 368.
Получу первое неполное произведение: 1 368.
В десятках второго множителя – ноль, поэтому пропускаем этап умножения на десятки.
Умножу первый множитель на число сотен:
456 ∙ 8 = 3 648.
Получу второе неполное произведение: 3 648 сот.
Начну подписывать второе неполное произведение под сотнями.
Сложу неполные произведения.
Читаю ответ: 366 168. Это произведение чисел 456 и 803.
Пишу: 605 ∙ 102.
Умножу первый множитель на число единиц:
605 ∙ 2 = 1 210.
Получу первое неполное произведение: 1 210.
В десятках второго множителя – ноль, поэтому пропускаем этап умножения на десятки.
Умножу первый множитель на число сотен:
605 ∙ 1 = 605.
Получу второе неполное произведение: 605 сот.
Начну подписывать второе неполное произведение под сотнями.
Сложу неполные произведения.
Читаю ответ: 61 710. Это произведение чисел 605 и 102.
Пишу: 105 ∙ 420.
Ноль смещаем вправо и не учитываем его в умножении.
Умножу первый множитель на число единиц:
105 ∙ 2 = 210.
Получу первое неполное произведение: 210.
Умножу первый множитель на число десятков:
105 ∙ 4 = 420.
Получу второе неполное произведение: 420 дес.
Начну подписывать второе неполное произведение под десятками.
Сложу неполные произведения. Допишу к ответу ноль из второго множителя.
Читаю ответ: 44 100. Это произведение чисел 105 и 420.
Пишу: 521 ∙ 180.
Ноль смещаем вправо и не учитываем его в умножении.
Умножу первый множитель на число единиц:
521 ∙ 8 = 4 168.
Получу первое неполное произведение: 4 168.
Умножу первый множитель на число десятков:
521 ∙ 1 = 521.
Получу второе неполное произведение: 521 дес.
Начну подписывать второе неполное произведение под десятками.
Сложу неполные произведения. Допишу к ответу ноль из второго множителя.
Читаю ответ: 93 780. Это произведение чисел 521 и 180.

Оформляем задание в тетрадь.

Номер 187.
Двум классам поручено расчистить школьный каток, длины которого 20 м, а ширина 10 м. В одном классе 26 учеников, а в другом 24. Сколько квадратных метров должен расчистить каждый класс, если распределить работу по числу учеников?
Ответ:
1) 20 ∙ 10 = 200 (м²) – площадь катка.
2) 26 + 24 = 50 (уч.) – в двух классах всего.
3) 200 : 50 = 4 (м²) – должен расчистить один ученик.
4) 4 ∙ 26 = 104 (м²) – должны расчистить ученики первого класса.
5) 4 ∙ 24 = 96 (м²) – должны расчистить ученики второго класса.
Ответ: 104 м² должны расчистить ученики первого класса и 96 м² должны расчистить ученики второго класса.
Повтори, как найти площадь прямоугольника, случаи вне табличного умножения.
Оформляем условие в виде таблицы.

Рассуждаем.
Длина катка 20 м, а ширина 10 м. Чтобы узнать площадь катка, нужно его длину умножить на ширину.
1) 20 ∙ 10 = 200 (м²) – площадь катка.
Продолжаем рассуждение.
В одном классе 26 учеников, а в другом 24. Вычислим, сколько учеников в двух классах.
2) 26 + 24 = 50 (уч.) – в двух классах всего.
Продолжаем рассуждение.
Площадь катка – 200 м², которую должны расчистить 50 учеников. Вычислим, сколько квадратных метров должен расчистить 1 ученик.
3) 200 : 50 = 4 (м²) – должен расчистить один ученик.
Продолжаем рассуждение.
1 ученик должен расчистить 4 м², в одном классе – 26 учеников. Узнаем, сколько квадратных метров должен расчистить этот класс.
4) 4 ∙ 26 = 104 (м²) – должны расчистить ученики первого класса.
Продолжаем рассуждение.
1 ученик должен расчистить 4 м², в одном классе – 24 ученика. Узнаем, сколько квадратных метров должен расчистить этот класс.
5) 4 ∙ 24 = 96 (м²) – должны расчистить ученики второго класса.
Записываем ответ.
Ответ: 104 м² и 96 м².
Номер 188.
У фермера 4 лошади и 9 коров. Лошади требуется на месяц 135 кг сена, а трём коровам – столько сена, сколько необходимо семи лошадям. Сколько килограммов сена должен расходовать фермер ежемесячно на всех лошадей и коров?
Ответ:4 лошади и 9 коров = ? кг сена всего 1 лошадь = 135 кг сена 3 коровы = 7 лошадей = ? кг сена
1) 135 ∙ 7 = 945 (кг) – сена нужно для 7 лошадей или 3 коров.

2) 9 : 3 = 3 (р.) – 9 коров больше в 3 раза, чем 3 коровы. 3) 945 ∙ 3 = 2835 (кг) – сена нужно для 9 коров.

4) 135 ∙ 4 = 540 (кг) – сена нужно для 4 лошадей.

5) 2835 + 540 = 3375 (кг) - сена на всех лошадей и коров.


Ответ: 3375 кг сена должен расходовать фермер ежемесячно на всех лошадей и коров.
Повтори единицу массы – килограмм.
Оформляем условие в виде краткой записи.
4 лошади и 9 коров = ? кг сена всего
1 лошадь = 135 кг сена
3 коровы = 7 лошадей = ? кг сена
Рассуждаем.
Узнаем, сколько сена нужно в месяц для 3 коров.
1) 135 ∙ 7 = 945 (кг) – сена нужно для 3 коров.
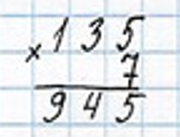
Продолжаем рассуждение.
Узнаем, во сколько раз 9 коров больше, чем 3 коровы.
2) 9 : 3 = 3 (р.) – 9 коров больше в 3 раза, чем 3 коровы.
Продолжаем рассуждение.
Узнаем, сколько сена нужно в месяц для 9 коров.
3) 945 ∙ 3 = 2835 (кг) – сена нужно для 9 коров.
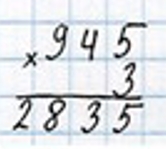
Продолжаем рассуждение.
Узнаем, сколько сена нужно в месяц для 4 лошадей.
4) 135 ∙ 4 = 540 (кг) – сена нужно для 4 лошадей.
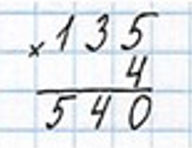
Продолжаем рассуждение.
Узнаем, сколько всего сена фермер должен расходовать ежемесячно на всех лошадей и коров.
5) 2835 + 540 = 3375 (кг)
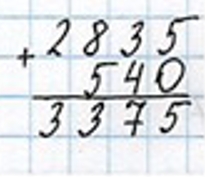
Записываем ответ.
Ответ: 3375 кг сена должен расходовать фермер ежемесячно на всех лошадей и коров.
Номер 189.
Высота футбольных ворот 2 м 40 см, она в 2 раза больше высоты хоккейных ворот. Узнай высоту хоккейных ворот.
Ответ:
Уточним, почему задача решается таким арифметическим действием: высота футбольных ворот - 2 м 40 см, что в 2 раза больше, чем высота хоккейных ворот. Получается, что высота хоккейных ворот в два раза меньше, и вычисляется делением.
2 м 40 см = 240 см
240 : 2 = 120 (см) – высота хоккейных ворот.
Ответ: высота хоккейных ворот составляет 1 м 20 см.
Повтори единицы длины – метр и сантиметр.
Оформляем условие в виде схематического чертежа.

Преобразуем метры в сантиметры.
Для удобства вычислений переведем метры в сантиметры.
2 м 40 см = 240 см
Рассуждаем.
Чтобы узнать высоту хоккейных ворот, нужно высоту футбольных ворот разделить на 2. Потому что известно, что хоккейные ворота в два раза ниже.
1) 240 : 2 = 120 (см) – высота хоккейных ворот.
Преобразуем сантиметры в метры.
120 см = 1 м 20 см
Записываем ответ.
Ответ: 1 м 20 см.
Номер 190.
1) Начерти отрезок длиной 8 см. Раздели его на 2 равные части. Какие доли отрезка получились? Сколько их? Раздели каждую половину ещё на 2 равные части. Какие доли отрезка получились? Сколько их в целом отрезке? Сколько четвёртых долей отрезка в его половине?
2) Раздели каждую четвёртую долю отрезка на 2 равные части. Какие доли отрезка получились? Сколько восьмых долей в трёх четвёртых отрезка?
Если разделить отрезок на 2 равные части, то получается две доли, которые можно назвать половина или одна вторая.

Разобъём каждую половину пополам. Получились 4 доли, которые называют четвёртые доли или одна четвёртая или четвертина.
.jpg)
Разобъём каждую четвёртую часть пополам. Получились 8 равных долей. Их называют восьмые доли или одна восьмая часть.
.jpg)
В трёх четвёртых отрезка шесть восьмых долей.
Повтори, что такое доли и отрезок, единицу длины – сантиметр.
Рассуждаем и выполняем вычисление.
Если разделить отрезок на 2 равные части, то получается две доли, которые можно назвать половина или одна вторая.

Разделим каждую половину еще на 2 равные части.
Разобьём каждую половину пополам. Получились 4 доли, которые называют четвёртые доли или одна четвёртая или четвертина.

Разделим каждую четвертую долю отрезка на 2 равные части.
Разобьём каждую четвёртую часть пополам. Получились 8 равных долей. Их называют восьмые доли или одна восьмая часть.
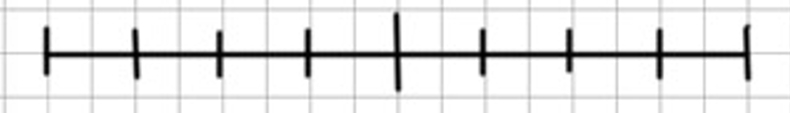
В трёх четвёртых отрезка шесть восьмых долей.
Задание внизу страницы
Ответ:
Повторите алгоритм письменного умножения на многозначное число, сложения и деления на двузначное число, а также порядок действий.
Выполняем вычисления с пояснениями.
Пишу: 528 ∙ 330.
Ноль смещаем вправо и не учитываем его в умножении.
Умножу первый множитель на число единиц:
528 ∙ 3 = 1 584.
Получу первое неполное произведение: 1 584.
Умножу первый множитель на число десятков:
528 ∙ 3 = 1 584.
Получу второе неполное произведение: 1 584 дес.
Начну подписывать второе неполное произведение под десятками.
Сложу неполные произведения. Допишу к ответу ноль из второго множителя.
Читаю ответ: 174 240. Это произведение чисел 528 и 330.
Пишу: 907 ∙ 203.
Умножу первый множитель на число единиц:
907 ∙ 3 = 2 721.
Получу первое неполное произведение: 2 721.
В десятках второго множителя – ноль, поэтому пропускаем этап умножения на десятки.
Умножу первый множитель на число сотен:
907 ∙ 2 = 1 814.
Получу второе неполное произведение: 1 814 сот.
Начну подписывать второе неполное произведение под сотнями.
Сложу неполные произведения.
Читаю ответ: 184 121. Это произведение чисел 907 и 203.
(634 100 – 17 300) : 300 = 2 056

Оформляем задание в тетрадь.

Задание на полях страницы
Сравни площади фигур.

Ответ:

Площади всех фигур одинаковые, потому что если мы разобьем квадрат на 2 треугольника, то увидим, что эти треугольники, равны треугольникам, из которых составлены фигуры 2 и 3, а это значит, что все фигуры равны.
Повтори, как найти площади фигур.
Рассмотрим фигуры на полях страницы.
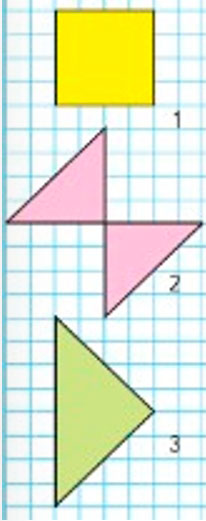
Сравним площади фигур.
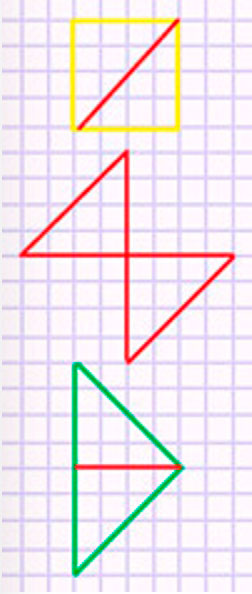
Площади всех фигур одинаковые, потому что если мы разобьем квадрат на 2 треугольника, то увидим, что эти треугольники, равны треугольникам, из которых составлены фигуры 2 и 3, а это значит, что все фигуры равны.
Номер 189.
1) Зал и коридор имеют одинаковую длину. Площадь зала 300 м², а площадь коридора 120 м². Ширина зала 10 м. Узнай, чему равна ширина коридора.
2) Используя ответ предыдущей задачи и чертёж, рассчитай, сколько метров линолеума шириной 2 м потребуется, чтобы покрыть полы в зале и коридоре.

Ответ:
Длина коридора = длина зала = х метров
Площадь коридора = 120 м²
Площадь зала = 300 м²
Ширина зала = 10 м
Ширина коридора = ? м
Задача 1:
1) 300 : 10 = 30 (м) – длина зала.
2) 120 : 30 = 4 (м) – ширина коридора.
Ответ: ширина коридора составляет 4 м.
Задача 2:
1) 300 + 120 = 420 (м²) – площадь зала и коридора.
2) 420 : 2 = 210 (м) – потребуется линолеума.
Ответ: 210 м линолеума потребуется для ремонта.
Номер 190.
Два самолёта летели с одинаковой скоростью. Первый самолёт был в воздухе 4 ч, второй – 6 ч. Первый самолёт пролетел на 1400 км меньше второго. Какое расстояние пролетел каждый самолёт?
Ответ:
1) 6 − 4 = 2 (ч) – на столько больше пролетел второй самолет, чем первый.
2) 1400 : 2 = 700 (км/ч) – скорость каждого самолёта.
3) 700 ∙ 4 = 2800 (км) – пролетел 1-ый самолёт.
4) 700 ∙ 6 = 4200 (км) – пролетел 2-ой самолёт.
Ответ: 2800 км всего пролетел первый самолёт и 4200 км всего протел второй самолёт.
Номер 191.
На молочной ферме каждой корове в сутки давали 3 кг сена. Это одна девятая часть всех кормов, которые она получала. Сколько всего килограммов корма давали в сутки 65 коровам?
Ответ:
1) 3 ∙ 9 = 27 (кг) – съедает одна корова в сутки. 2) 27 ∙ 65 = 1755 (кг) – съедает 65 коров в сутки.

Ответ: 1755 кг сена всего съедает 65 коров в сутки.
Номер 192.
Ответ:
1 см² − 10 мм² = 100 мм² − 10 мм² = 90 мм²
1 см² − 1 мм² = 100 мм² − 1 мм² = 99 мм²
1 м² − 10 дм² = 100 дм² − 10 дм² = 90 дм²
1 м² − 1000 см² = 10000 см² − 1000 см² = 9000 см²
1 дм² − 5 см² = 100 см² − 5 см² = 95 см²
1 дм² − 50 см² = 100 см² − 50 см² = 50 см²
Номер 193.
Найди ошибки, выполни деление и сделай проверку.


При решении первого примера ошибка в том, что второе неполное делимое 7 и второе неполное делимое 72 были меньше 90, но перед списыванием следующей цифры не записывали 0 в частное.
Второй пример решен верно.
При решении третьего примера ошибка в том, что после того как все десятки полностью разделили, не стали списывать для деления единицы. Однако и ноль не приписали в частное.
Номер 194.
Реши уравнения.
Ответ:
Номер 195.
Ответ:

Номер 196.
У Ивана и Петра вместе 980 р., у Ивана и Никиты вместе 930 р., а у Петра и Никиты вместе 890 р. Сколько денег у каждого из них? Проверь решение.
Ответ:
1) (980 + 890 + 930) : 2 = 1400 (р.) – у всех мальчиков вместе.
2) 1400 − 980 = 420 (р.) – у Никиты.
3) 1400 − 930 = 470 (р.) – у Петра.
4) 1400 − 890 = 510 (р.) – у Ивана.
Проверка:
420 + 510 = 930 (р.) – у Ивана и Никиты вместе.
510 + 470 = 980 (р.) – у Ивана и Петра вместе.
470 + 420 = 890 (р.) – у Петра и Никиты вместе.
Ответ: 470 рублей у Петра, 420 рублей у Никиты, 510 рублей у Ивана.
Задание внизу страницы


Задание на полях страницы
Ребус.

Ответ:

С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.