Математика 4 класс учебник Моро, Бантова 1 часть ответы – страница 92

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 12.
Дима купил для украшения ёлки 4 игрушки по одинаковой цене, а Настя – 3 такие же игрушки. Все эти игрушки стоили 56 р. Объясни, что обозначают выражения.
Ответ:3 + 4 – число всех купленных игрушек. 56 : (3 + 4) – цена одной игрушки. 56 : (3 + 4) ∙ 3 – стоимость игрушек купленных Настей. 56 : (3 + 4) ∙ 4 – стоимость игрушек купленных Димой.
Помни о том, каков конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а ∙ 3, а – первый множитель, а 3 – количество множителей.
Помни о зависимости между компонентами и результатом действия умножения:
1 множитель ∙ 2 множитель = значение произведения.
Значение произведения : 1 множитель = 2 множитель.
Значение произведения : 2 множитель = 1 множитель.
Данная задача: вида «цена товара, количество товаров, общая стоимость товаров» характеризуется зависимостями между компонентами:
Цена товара ∙ количество товаров = общая стоимость товаров
Общая стоимость товаров : количество товаров = цена товара
Общая стоимость товаров : цена товара = количество товаров
Оформим условие в виде таблицы.

Объясним, что обозначают выражения:
3 + 4 – число всех купленных игрушек.
56 : (3 + 4) – цена одной игрушки.
56 : (3 + 4) ∙ 3 – стоимость игрушек купленных Настей.
56 : (3 + 4) ∙ 4 – стоимость игрушек купленных Димой.
Оформим задание в тетрадь.
Номер 13.
Мальчик купил 6 тетрадей в клетку и 5 тетрадей в линейку по одинаковой цене. Всего он заплатил d р. Объясни, что обозначают выражения.
Ответ:6 + 5 – число купленных тетрадей. d : (6 + 5) – цена одной тетради. d : (6 + 5) ∙ 6 – стоимость тетрадей в клетку.
Помни о том, каков конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а ∙ 3, а – первый множитель, а 3 – количество множителей.
Помни о зависимости между компонентами и результатом действия умножения:
1 множитель ∙ 2 множитель = значение произведения.
Значение произведения : 1 множитель = 2 множитель.
Значение произведения : 2 множитель = 1 множитель.
Данная задача: вида «цена товара, количество товаров, общая стоимость товаров» характеризуется зависимостями между компонентами:
Цена товара ∙ количество товаров = общая стоимость товаров.
Общая стоимость товаров : количество товаров = цена товара.
Общая стоимость товаров : цена товара = количество товаров.
Оформим условие в виде таблицы.

Объясним, что обозначают выражения:
6 + 5 – число купленных тетрадей.
d : (6 + 5) – цена одной тетради.
d : (6 + 5) ∙ 6 – стоимость тетрадей в клетку.
Оформим задание в тетрадь.
Номер 14.
В одном куске 5 м ткани, в другом куске 7 м такой же ткани. За оба куска заплатили k р. Объясни, что обозначают выражения.
Ответ:k : (5 + 7) – цена 1 м ткани. k : (5 + 7) ∙ 5 – стоимость 5 м ткани. k : (5 + 7) ∙ 7 – стоимость 7 м ткани.
Помни о том, каков конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а ∙ 3, а – первый множитель, а 3 – количество множителей.
Помни о зависимости между компонентами и результатом действия умножения:
1 множитель ∙ 2 множитель = значение произведения.
Значение произведения : 1 множитель = 2 множитель.
Значение произведения : 2 множитель = 1 множитель.
Данная задача: вида «цена 1 метра ткани, количество ткани, общая стоимость ткани» характеризуется зависимостями между компонентами:
Цена 1 метра ткани ∙ количество ткани = общая стоимость ткани.
Общая стоимость ткани : количество ткани = цена 1 метра ткани.
Общая стоимость ткани : цена 1 метра ткани = количество ткани.
Оформим условие в виде таблицы.

Объясним, что обозначают выражения:
k : (5 + 7) – цена 1 м ткани.
k : (5 + 7) ∙ 5 – стоимость 5 м ткани.
k : (5 + 7) ∙ 7 – стоимость 7 м ткани.
Оформим задание в тетрадь.
Номер 15.
Расставь скобки так, чтобы равенства стали верными.
Ответ:(78 − 60) : 2 + 4 = 13 78 − (60 : 2 + 4) = 44
Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий. Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
Вычисление значений выражения сводится к применению правил:
Правило прибавления суммы к числу: а + (в + с) = (а + в) + с
Правило вычитания числа из суммы: (а + в) – с = (а – с) + в
Выполним вычисления с объяснением.
(78 – 60) : 2 + 4 = 13
1) 78 – 60 = (70 + 8) – 60 = (70 – 60) + 8 = 10 + 8 = 18, по правилу вычитания числа из суммы
2) 18 : 2 = 9, потому что 2 ∙ 9 = 18, это по 2 – 9 раз, где 2 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых
3) 9 + 4 = 9 + (1 + 3) = (9 + 1) + 3 = 10 + 3 = 13, по правилу прибавления суммы к числу
78 – (60 : 2 + 4) = 44
1) 60 : 2 = 30, потому что 2 ∙ 30 = 60, это по 2 – 30 раз, где 2 – одинаковое слагаемое, а 30 – количество одинаковых слагаемых
2) 30 + 4 = 34, по правилу замены суммы разрядных слагаемых числом
3) 78 – 34 = (74 + 4) – 34 = (74 – 34) + 3 = 40 + 4 = 44, по правилу вычитания числа из суммы
Оформим задание в тетрадь.
(78 − 60) : 2 + 4 = 13
78 − (60 : 2 + 4) = 44
Номер 16.
Во сколько раз 1 дм больше, чем 1 мм? 1 ц больше, чем 10 кг? 1 ч больше, чем 10 мин? 1 км больше, чем 100 м? 1 м2 больше чем 1 см2?
Ответ:1 дм в 100 раз больше, чем 1 мм 1 ц в 10 раз больше, чем 10 кг. 1 ч в 6 раз больше, чем 10 мин. 1 км в 10 раз больше, чем 100 м. 1 м2 в 10000 раз больше, чем 1 см2
Чтобы узнать, во сколько раз одно число больше другого, нужно большее число разделить на меньшее. Вычисляется делением.
Масса – величина, которая характеризует вес предмета, то, сколько он весит. Масса может измеряться в таких единицах измерения, как грамм, килограмм, центнер, тонна.
Помни о соотношении числовых значений единиц измерения времени:
1 кг = 1000 г
1 ц = 100 кг
1 т = 1000 кг
Площадь – величина, которая характеризует размер части плоскости, занятой фигурой. Измеряется в таких единицах измерения, как: мм2, см2, дм2, м2, км2 и др.
Помни о соотношении числовых значений единиц измерения площади:
1 см2 = 100 мм2
1 дм2 = 100 см2
1 м2 = 10 000 см2
1 м2 = 100 дм2
Длина – величина, характеризующая протяженность объекта на плоскости, выражается в таких единицах измерения, как миллиметр, сантиметр, дециметр, метр, километр.
Помни о соотношении числовых значений единиц измерения длины:
1 см = 10 мм
1 дм = 10 см
1 м = 100 см
1 м = 10 дм
1 км = 1000 м
Время – величина, характеризующая продолжительность какого-либо события и отношения его к временной прямой: прошлому, настоящему или будущему. Измеряется в таких единицах измерения, как: 1 секунда, 1 минута, 1 час, 1 сутки, 1 неделя, 1 месяц, 1 год, 1 век.
Помни о соотношении числовых значений единиц измерения времени:
1 мин – 60 сек
1 час – 60 мин
1 сут – 24 час
1 мес – 28, 29, 30 или 31 сут.
1 год – 12 мес
1 год – 356 сут.
Выполним вычисления с объяснением.
1 дм и 1 мм
1 дм – 10 см, а 1 см – 10 мм, значит, 1 дм – 100 мм. Тогда, 100 мм : 1 мм = 100 – во столько раз 1 дм больше, чем 1 мм.
1 ц и 10 кг
1 ц – 100 кг, тогда, 100 кг : 10 кг = 10 – во столько раз 1 ц больше, чем 10 кг
1 ч и 10 мин
1 ч – 60 мин, значит, 60 мин : 10 мин = 6 – во столько раз 1 час больше 10 минут
1 км и 100 м
1 км – 1 000 м, значит, 1 000 м : 100 м = 10 – во столько раз 1 км больше 100 м
1 м2 и 1 см2
1 м2 – это 10 000 см2, потому что 100 см ∙ 100 см = 10 000 см2, значит, 10 000 см2 : 1 см2 = 10 000 – во столько раз больше 1 м2 чем 1 см2.
Оформим задание в тетрадь.
1 дм в 100 раз больше, чем 1 мм.
1 ц в 10 раз больше, чем 10 кг.
1 ч в 6 раз больше, чем 10 мин.
1 км в 10 раз больше, чем 100 м.
1 м2 в 10000 раз больше, чем 1 см2
Номер 17.
Спортсмен прыгнул в высоту на 2 и 35 см, это на 49 см выше его роста. Какого роста был этот спортсмен?
Ответ:
2 м 35 см – 49 см = 1 м 86 см 2 м 35 см = 235 см

186 см = 1 м 86 см – рост спортсмена
Ответ: 1 м 86 см рост спортсмена.
Условно задача в косвенной форме формулируется так: это на столько-то больше, чем то.
Задача в косвенной форме решается в зависимости от вопроса: «это на х больше», значит, решается вычитанием, а если: «это на х меньше», значит, решается сложением.
«это на 49 см выше», значит, вычисляется вычитанием, потому что задача в косвенной форме.
Оформляем условие в виде краткой записи.

Выполняем проверку.
Спортсмен прыгнул на в высоту на 2 м 35 см. Это на 49 см выше его роста. Получается, что его рост на 49 см меньше, чем высота прыжка. Значит, чтобы узнать, какой рост у спортсмена, нужно из высоты прыжка вычесть 49 см.
2 м 35 см – 49 см = 1 м 86 см
2 м 35 см = 235 см
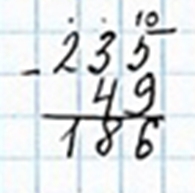
186 см = 1 м 86 см
Записываем ответ.
Ответ: 1 м 86 см рост спортсмена.
Номер 18.
Хлебозавод ежедневно выпекал одинаковое количество хлеба. За 3 дня было выпечено 705 т хлеба. Сколько хлеба было выпечено за неделю?
Ответ:

Помни о том, каков конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а ∙ 3, а – первый множитель, а 3 – количество множителей.
Помни о зависимости между компонентами и результатом действия умножения:
1 множитель ∙ 2 множитель = значение произведения.
Значение произведения : 1 множитель = 2 множитель.
Значение произведения : 2 множитель = 1 множитель.
Данная задача: вида «количество хлеба в 1 день, количество дней, общее количество хлеба» характеризуется зависимостями между компонентами:
Количество хлеба в 1 день ∙ кол-во дней = общее кол-во хлеба.
Общее кол-во хлеба : кол-во дней = количество хлеба в 1 день.
Общее кол-во хлеба : количество хлеба в 1 день = кол-во дней.
Оформляем условие в виде таблицы.

Рассуждаем.
Чтобы узнать, сколько хлеба выпекали в 1 день, нужно общее количество хлеба разделить на количество дней.
1) 705 : 3 = 235 ( т.) – выпекают за 1 день
Продолжаем рассуждение.
Чтобы узнать, сколько хлеба испекли всего, нужно количество хлеба 1 дня умножить на количество дней.
2) 1 нед. = 7 дн.
3) 235 ∙ 7 = 1 645 (т.)
Записываем ответ.
Ответ: 1 645 тонн выпекают за неделю
Решение выражением: (705 : 3) ∙ 7, где 705 : 3 – количество выпекаемого хлеба в день
Оформляем задание в тетрадь.

Номер 19.
За 3 ч езды на легковой машине израсходовали 27 л бензина. На сколько часов езды хватит 96 л бензина, если расход его уменьшится на 1 л в час.
Ответ:
1) 27 : 3 = 9 (л) – расход бензина за 1 час был.
2) 9 − 1 = 8 (л) – расход бензина за 1 час стал.
3) 96 : 8 = 12 (ч) – может ездить автомобиль.
Ответ: 12 часов может ездить автомобиль.
Помни о том, каков конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а ∙ 3, а – первый множитель, а 3 – количество множителей.
Помни о зависимости между компонентами и результатом действия умножения:
1 множитель ∙ 2 множитель = значение произведения.
Значение произведения : 1 множитель = 2 множитель.
Значение произведения : 2 множитель = 1 множитель.
Данная задача: вида «расход бензина в 1 час, количество часов, общий расход бензина» характеризуется зависимостями между компонентами:
Расход бензина в 1 час ∙ количество часов = общий расход бензина.
Общий расход бензина : количество часов = расход бензина в 1 час.
Общий расход бензина : расход бензина в 1 час = количество часов.
Оформляем условие в виде таблицы.
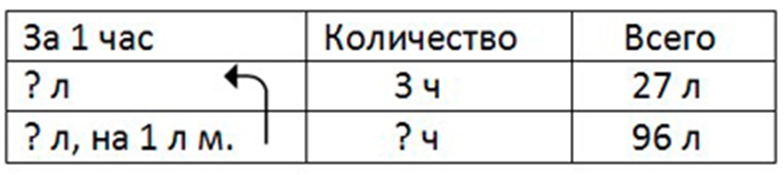
Рассуждаем.
Чтобы узнать, сколько бензина расходовалось в 1 час, нужно общий расход бензина разделить на количество часов.
1) 27 : 3 = 9 (л) – расход бензина за 1 час был.
Продолжаем рассуждение.
Чтобы узнать, каким будет расход бензина, нужно из прошлого расхода вычесть 1 м.
2) 9 − 1 = 8 (л) – расход бензина за 1 час стал.
Продолжаем рассуждение.
Чтобы узнать, на сколько часов хватит бензина, нужно общее количество бензина разделить на расход бензина в 1 час.
3) 96 : 8 = 12 (ч)
Записываем ответ.
Ответ: 12 часов может ездить автомобиль.
Номер 20.
Вычисли результат и выполни проверку.
Ответ:
Помни о том, что существует алгоритм письменного деления. Следуй ему, объясняя, как выполняешь деление:
1) Выделю первое неполное делимое, чтобы определить количество цифр в частном.
2) Нахожу цифру сотен в частном.
3) Нахожу, сколько сотен разделили.
4) Нахожу, сколько сотен осталось разделить.
5) Образую второе неполное делимое.
6) Нахожу, количество десятков в частном.
7) Нахожу, сколько десятков разделили.
8) Нахожу, сколько десятков осталось разделить.
9) Образую третье неполное делимое.
10) Нахожу количество единиц в частном.
11) Нахожу, сколько единиц разделили.
12) Нахожу, сколько единиц осталось разделить.
13) Читаю ответ.
Помни о том, что существует алгоритм объяснения умножения трехзначного числа на однозначное. Следуй ему:
1) Записываю первый множитель так, чтобы каждая цифра стояла в своей клетке. Ставлю знак умножить.
2) Записываю второй множитель так, чтобы разряд стоял под разрядом.
3) Провожу черту, обозначающую знак равно.
4) Умножение начинаю с единиц низшего разряда.
5) Умножаю десятки.
6) Умножаю сотни.
7) Умножение окончено. Читаю ответ.
Следуй плану при устном объяснении вычитания в столбик:
1) Записываю уменьшаемое так, чтобы каждая цифра стояла в своей клетке. Ставлю знак минус.
2) Записываю вычитаемое так, чтобы разряд стоял под разрядом.
3) Провожу черту, обозначающую знак равно.
4) Вычитание начинаю с единиц низшего разряда. Вычитаю единицы.
5) Вычитаю десятки.
6) Вычитаю сотни.
7) Вычитание окончено. Читаю ответ.
Вспомни названия компонентов действия сложения, вычитания, умножения и деления и зависимость между компонентами и результатом действий сложения, вычитания, умножения и деления:
1 слагаемое + 2 слагаемое = значение суммы;
значение суммы − 1 слагаемое = 2 слагаемое;
значение суммы − 2 слагаемое = 1 слагаемое;
уменьшаемое - вычитаемое = значение разности;
уменьшаемое - значение разности = вычитаемое;
значение разности + вычитаемое = уменьшаемое;
1 множитель ∙ 2 множитель = значение произведения;
значение произведения : 1 множитель = 2 множитель;
значение произведения : 2 множитель = 1 множитель;
делимое : делитель = значение частного;
делимое : значение частного = делитель;
значение частного ∙ делитель = делимое.
Рассуждаем и выполняем вычисление.
Пишу: 45 845 + 3 509.
Складываю единицы: 5 + 9 = 14. 14 ед. – это 1 дес. и 4 ед.; 4 ед. пишу под единицами, а 1 дес. прибавлю к десяткам.
Складываю десятки: 4 + 0 = 4, да ещё 1.
4 + 1 = 5. Пишу 5 под десятками.
Складываю сотни: 8 + 5 = 13.
13 сот. – это 1 ед. тыс. и 3 сот.; 3 сот. пишу под сотнями, а 1 ед. тыс. прибавлю к ед. тыс.
Складываю единицы тысяч: 5 + 3 = 8, да ещё 1. 8 + 1 = 9. Пишу 9 под единицами тысяч.
Пишу 4 под десятками тысяч, так как других десятков тысяч для сложения нет.
Читаю ответ: 49 354.
Чтобы проверить сложение, можно из суммы вычесть одно из слагаемых и в результате вычислений должно получиться другое слагаемое.
Пишу: 50 102 - 6 945.
Вычитаю единицы: из 2 ед. нельзя вычесть 5 ед. Взять 1 дес. из 0 дес. нельзя, поэтому беру 1 сот. из 1 сот. (Чтобы не забыть об этом, ставлю точку над цифрой 1.) 1 сот. – это 10 дес. (Чтобы не забыть об этом, ставлю точку над цифрой 0.) 1 дес. и 2 ед. – это 12 ед. Из 12 вычесть 5, получится 7. Пишу под единицами 7.
Вычитаю десятки: было 10 дес., но 1 дес. взяли при вычитании единиц, осталось 9 дес. Из 9 вычесть 4, получится 5. Пишу под десятками 5.
Вычитаю сотни: была 1 сот., но 1 сот. взяли при вычитании единиц, осталось 0 сот. Из 0 сот. нельзя вычесть 9 сот. Взять 1 ед. тыс. из 0 нельзя, поэтому беру 1 дес. тыс. из 5 дес. тыс. (Чтобы не забыть об этом, ставлю точку над цифрой 5). 1 дес. тыс. – это 10 ед. тыс. Из 10 ед. тыс. беру 1 ед. тыс. (Чтобы не забыть об этом, ставлю точку над цифрой 0). 1 ед. тыс. и 0 сот. - это 10 сот. Из 10 вычесть 9, получится 1. Пишу под сотнями 1.
Вычитаю единицы тысяч: было 10 ед. тыс., но 1 ед. тыс. взяли при вычитании сотен, осталось 9 ед. тыс. Из 9 вычесть 6, получится 3. Пишу 3 под единицами тысяч.
Вычитаю десятки тысяч: было 5 дес. тыс., но 1 дес. тыс. взяли при вычитании сотен, осталось 4 дес. тыс. Пишу 4 под дес. тыс., так как разряд десятков тысяч в вычитаемом отсутствует.
Читаю ответ: 43 157.
Чтобы проверить вычитание, можно к разности прибавить вычитаемое и в результате вычислений должно получиться уменьшаемое.
Пишу: 7 306 ∙ 4.
Умножаю единицы: 6 ∙ 4 = 24. 24 ед. – это 2 дес. и 4 ед., 4 ед. пишу под единицами, а 2 дес. запомню и прибавлю к десяткам после умножения десятков.
Умножаю десятки: 0 ∙ 4 = 0. К 0 дес. прибавляю 2 дес., которые получены при умножении единиц: 0 + 2 = 2. Пишу 2 под десятками.
Умножаю сотни: 3 ∙ 4 = 12. 12 сот. – это 1 ед. тыс. и 2 сот.; 2 сот. пишу под сотнями, а 1 ед. тыс. запомню и прибавлю к единицам тысяч после умножения единиц тысяч.
Умножаю единицы тысяч: 7 ∙ 4 = 28. К 28 ед. тыс. прибавляю 1 ед. тыс, которые получены при умножении сотен: 28 + 1 = 29. 29 ед. тыс. - это 2 дес. тыс. и 9 ед. тыс.; 9 ед. тыс. пишу под единицами тысяч, а 2 дес. тыс. запишу под десятками тысяч, так как других десятков тысяч для умножения нет.
Читаю ответ: 29 224.
Чтобы проверить умножение, можно произведение разделить на один из множителей и в результате вычислений должен получиться другой множитель.
Пишу: 87 540 : 6.
Делю единицы тысяч.
8 дес. тыс. – это первое неполное делимое, значит в записи частного будет 5 цифр.
Разделю 8 на 6, получу 1 – столько десятков тысяч будет в частном.
Умножу 1 на 6, получу 6 – столько десятков тысяч разделили.
Вычту 6 из 8, получу 2 – столько десятков тысяч осталось разделить.
Сравню остаток с делителем: число оставшихся тысяч меньше, чем 6.
Делю единицы тысяч.
2 дес. тыс. 7 ед. тыс. – всего 27 ед. тыс. Это второе неполное делимое.
Разделю 27 на 6, получу 4 – столько единиц тысяч будет в частном.
Умножу 4 на 6, получу 24 – столько единиц тысяч разделили.
Вычту 24 из 27, получу 3 – столько единиц тысяч осталось разделить.
Сравню остаток с делителем: число оставшихся сотен меньше, чем 6.
Делю сотни.
3 ед. тыс. 5 сот. – всего 35 сот. Это третье неполное делимое.
Разделю 35 на 6, получу 5 – столько сотен будет в частном.
Умножу 5 на 6, получу 30 – столько сотен разделили.
Вычту 30 из 35, получу 5 – столько сотен осталось разделить.
Сравню остаток с делителем: число оставшихся сотен меньше, чем 6.
Делю десятки.
5 сот. 4 дес. – всего 54 дес. Это четвёртое неполное делимое.
Разделю 54 на 6, получу 9 – столько десятков будет в частном.
Умножу 9 на 6, получу 54 – столько десятков разделили.
Вычту 54 из 54, получу 0 – десятки разделили все.
0 ед. нельзя разделить так, чтобы в частном получились единицы.
Читаю ответ: 14 590.
Чтобы проверить деление, можно частное умножить на делитель и в результате вычислений должно получиться делимое.
Оформим задание в тетрадь.

Номер 21.
Реши уравнения.
Ответ:
х : 9 = 11
х = 11 ∙ 9
х = 99
Проверка:
99 : 9 = 11
11 = 11
Ответ: х = 99
х + 75 = 2075
х = 2075 − 75
х = 2000
Проверка:
2000 + 75 = 2075
2075 = 2075
Ответ: х = 2000
х ∙ 8 = 720
х = 720 : 8
х = 90
Проверка:
90 ∙ 8 = 720
720 = 720
Ответ: х = 90
х − 80 = 360
х = 360 + 80
х = 440
Проверка:
440 − 80 = 360
360 = 360
Ответ: х = 440
56 : х = 56
х = 56 : 56
х = 1
Проверка:
56 : 1 = 56
56 = 56
Ответ: х = 1
90 − х = 90
х = 90 − 90
х = 0
Проверка:
90 − 0 = 90
90 = 90
Ответ: 0
Уравнение – равенство с неизвестной, при подстановке числа в которую, получается верное равенство.
Вспомни названия компонентов действия умножения, и зависимость между компонентами и результатом действия умножения:
1 множитель ∙ 2 множитель = значение произведения.
Значение произведения : 1 множитель = 2 множитель.
Значение произведения : 2 множитель = 1 множитель.
Уменьшаемое – вычитаемое = значение разности.
Уменьшаемое – значение разности = вычитаемое.
Значение разности + вычитаемое = уменьшаемое.
Делимое : делитель = значение разности.
Делимое : значение разности = делитель.
Значение разности ∙ делитель = делимое.
Решим уравнения.
х : 9 = 11
х = 11 ∙ 9
х = 99
Проверка:
99 : 9 = 11
11 = 11
х + 75 = 2075
х = 2075 − 75
х = 2000
Проверка:
2000 + 75 = 2075
2075 = 2075
х ∙ 8 = 720
х = 720 : 8
х = 90
Проверка:
90 ∙ 8 = 720
720 = 720
х − 80 = 360
х = 360 + 80
х = 440
Проверка:
440 − 80 = 360
360 = 360
56 : х = 56
х = 56 : 56
х = 1
Проверка:
56 : 1 = 56
56 = 56
90 − х = 90
х = 90 − 90
х = 0
Проверка:
90 − 0 = 90
90 = 90
Выполняем проверку.
Оформим задание в тетрадь
Номер 22.
Найди значение выражения c − k, если c — наименьшее семизначное число, k — наибольшее шестизначное число.
Ответ:1000000 − 999999 = 1
с – к – разность, основано на арифметическом действии вычитания
Семизначное число – число, в котором 7 знаков
Шестизначное число – число, в котором 6 знаков
Найдем значение выражения с – k.
Наименьшее семизначное число, т.е. расположенное на луче семизначных числе левее всего. Это число 1 000 000 – один миллион
Наибольшее шестизначное число, т.е. расположенное на луче шестизначных чисел правее всего. Это число 999 999 – девятьсот девяносто девять тысяч девятьсот девяносто девять.
с – k = 1000000 − 999999 = 1
Оформим задание в тетрадь.
1000000 − 999999 = 1
Номер 12.
Дима купил для украшения ёлки 4 игрушки по одинаковой цене, а Настя – 3 такие же игрушки. Все эти игрушки стоили 56 р. Объясни, что обозначают выражения.
Ответ:3 + 4 – число всех купленных игрушек. 56 : (3 + 4) – цена одной игрушки. 56 : (3 + 4) ∙ 3 – стоимость игрушек купленных Настей. 56 : (3 + 4) ∙ 4 – стоимость игрушек купленных Димой.
Номер 13.
Мальчик купил 6 тетрадей в клетку и 5 тетрадей в линейку по одинаковой цене. Всего он заплатил d р. Объясни, что обозначают выражения.
Ответ:6 + 5 – число купленных тетрадей. d : (6 + 5) – цена одной тетради. d : (6 + 5) ∙ 6 – стоимость тетрадей в клетку.
Номер 14.
В одном куске 5 м ткани, в другом куске 7 м такой же ткани. За оба куска заплатили k р. Объясни, что обозначают выражения.
Ответ:k : (5 + 7) – цена 1 м ткани. k : (5 + 7) ∙ 5 – стоимость 5 м ткани. k : (5 + 7) ∙ 7 – стоимость 7 м ткани.
Номер 15.
Как можно, не изменяя чисел, сделать равенства верными? Выполни это.
78 – 60 : 2 + 4 = 13 78 – 60 : 2 + 4 = 44
Ответ:Нужно расставить скобки.
(78 – 60) : 2 + 4 = 18 : 2 + 4 = 9 + 4 = 13
78 – (60 : 2 + 4) = 78 – (20 + 4) = 78 – 34 = 44
Номер 16.
Во сколько раз 1 дм больше, чем 1 мм? 1 ц больше, чем 10 кг? 1 ч больше, чем 10 мин? 1 км больше, чем 100 м? 1 м2 больше чем 1 см2?
Ответ:1 дм в 100 раз больше, чем 1 мм 1 ц в 10 раз больше, чем 10 кг. 1 ч в 6 раз больше, чем 10 мин. 1 км в 10 раз больше, чем 100 м. 1 м2 в 10000 раз больше, чем 1 см2
Номер 17.
Спортсмен прыгнул в высоту на 2 и 35 см, это на 49 см выше его роста. Какого роста был этот спортсмен?
Ответ:
2 м 35 см – 49 см = 1 м 86 см 2 м 35 см = 235 см

186 см = 1 м 86 см
Ответ: 1 м 86 см рост спортсмена.
Номер 18.
Хлебозавод ежедневно выпекал одинаковое количество хлеба. За 3 дня было выпечено 705 т хлеба. Сколько хлеба было выпечено за неделю?
Ответ:

Номер 19.
За 3 ч езды на легковой машине израсходовали 27 л бензина. На сколько часов езды хватит 96 л бензина, если расход его уменьшится на 1 л в час.
Ответ:
1) 27 : 3 = 9 (л) –расход бензина за 1 час был.
2) 9 − 1 = 8 (л) – расход бензина за 1 час стал.
3) 96 : 8 = 12 (ч) – может ездить автомобиль
Ответ: 12 часов может ездить автомобиль.
Номер 20.
Вычисли результат и выполни проверку.
Ответ:
Номер 21.
Реши уравнения.
Ответ:х : 9 = 11
х = 11 ∙ 9
х = 99
99 : 9 = 11
11 = 11
х + 75 = 2075
х = 2075 − 75
х = 2000
2000 + 75 = 2075
2075 = 2075
х ∙ 8 = 720
х = 720 : 8
х = 90
90 ∙ 8 = 720
720 = 720
х – 80 = 360
х = 360 + 80
х = 440
440 – 80 = 360
360 = 360
56 : х = 56
х = 56 : 56
х = 1
56 : 1 = 56
56 = 56
90 – х = 90
х = 90 − 90
х = 0
90 – 0 = 90
90 = 90
Номер 22.
Найди значение выражения c – k, если c – наименьшее семизначное число, k – наибольшее шестизначное число.
Ответ:1000000 – 999999 = 1
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.