Математика 4 класс учебник Моро, Бантова 1 часть ответы – страница 91

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Что узнали. Чему научились
Номер 1.
Объясни, почему верны равенства.
Ответ:1-й способ решения:
1) 170 ∙ 3 + 170 = 170 ∙ 4
Умножение – это многократное повторение одного слагаемого.
С левой стороны число 170 сначала повторили 3 раза,
затем еще один раз. Значит всего 4 раза.
Справа число 170 повторили 4 раза.
Поэтому равенство равно.
560 ∙ 9 – 560 = 560 ∙ 8
Умножение – это многократное повторение одного слагаемого.
С левой стороны число 560 сначала повторили 9 раз,
затем один раз убрали. Значит всего 8 раз.
Справа число 560 повторили 8 раз.
Поэтому равенство равно.
96 ∙ 4 + 96 ∙ 6 = 96 ∙ 10
Умножение – это многократное повторение одного слагаемого.
С левой стороны число 96 сначала повторили 4 раза,
затем еще 6 раз. Значит всего 10 раз.
Справа число 96 повторили 10 раз.
Поэтому равенство равно.
45 ∙ 3 + 450 = 450 + 3 ∙ 45 – равенство верно
на основании переместительного свойства сложения.
2) (81 + 27) : 9 = 81 : 9 + 27 : 9 – равенство верно
на основе правила деления суммы чисел на число.
Чтобы разделить сумму на число, нужно каждое
слагаемое разделить, а результаты сложить.
(540 – 180) : 6 = 540 : 6 – 180 : 6 – равенство верно
на основании правила деления разности чисел на число.
Чтобы разделить разность на число, можно разделить
на это число отдельно уменьшаемое и вычитаемое,
а потом из первого частного вычесть второе.
1) При умножении суммы на число можно умножить на него каждое слагаемое в отдельности и полученные результаты сложить. Это правило действует и при умножении разности на число.
170 ∙ 3 + 170 = 170 ∙ 4
170 ∙ 3 + 170 ∙ 1 = 170 ∙ 4
170 ∙ (3 + 1) = 170 ∙ 4
170 ∙ 4 = 170 ∙ 4
560 ∙ 9 – 560 = 560 ∙ 8
560 ∙ 9 – 560 ∙ 1 = 560 ∙ 8
560 ∙ (9 – 1) = 560 ∙ 8
560 ∙ 8 = 560 ∙ 8
96 ∙ 4 + 96 ∙ 6 = 96 ∙ 10
96 ∙ (4 + 6) = 96 ∙ 10
96 ∙ 10 = 96 ∙ 10
45 ∙ 3 + 450 = 450 + 3 ∙ 45
45 ∙ 3 + 450 = 45 ∙ 3 + 450
2) При делении суммы на число можно разделить на него каждое слагаемое в отдельности и полученные результаты сложить. Это правило действует и при делении разности на число.
(81 + 27) : 9 = 81 : 9 + 27 : 9
81 : 9 + 27 : 9 = 81 : 9 + 27 : 9
(540 – 180) : 6 = 540 : 6 – 180 : 6
540 : 6 – 180 : 6 = 540 : 6 – 180 : 6
Помни о том, каков конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а ∙ 3, а – первый множитель, а 3 – количество множителей.
Объясняем, почему верны равенства.
Умножение – это многократное повторение одного слагаемого.
170 ∙ 3 + 170 = 170 ∙ 4
С левой стороны число 170 сначала повторили 3 раза, затем еще один раз. Значит всего 4 раза. Справа число 170 повторили 4 раза. Поэтому равенство равно.
560 ∙ 9 − 560 = 560 ∙ 8
С левой стороны число 560 сначала повторили 9 раз, затем один раз убрали. Значит всего 8 раз. Справа число 560 повторили 8 раз. Поэтому равенство равно.
96 ∙ 4 + 96 ∙ 6 = 96 ∙ 10
С левой стороны число 96 сначала повторили 4 раза, затем еще 6 раз. Значит всего 10 раз. Справа число 96 повторили 10 раз. Поэтому равенство равно.
45 ∙ 3 + 450 = 450 + 3 ∙ 45 – равенство верно на основании переместительного свойства сложения.
Продолжаем объяснения.
(81 + 27) : 9 = 81 : 9 + 27 : 9 – равенство верно на основе правила деления суммы чисел на число. Чтобы разделить сумму на число, нужно каждое слагаемое разделить, а результаты сложить.
(540 − 180) : 6 = 540 : 6 − 180 : 6 – равенство верно на основании правила деления разности чисел на число. Чтобы разделить разность на число, можно разделить на это число отдельно уменьшаемое и вычитаемое, а потом из первого частного вычесть второе.
Оформляем задание в тетрадь.
Номер 2.
Ответ:
Помни о том, что в математике существуют свойства арифметических действий: переместительное, сочетательное, распределительное – они характерны для многих арифметических действий, а есть особые свойства, которые для каждого арифметического действия свои:
Правило прибавления числа к единице: 1 + а;
Правило прибавления единицы к числу: а + 1;
Правило прибавления нуля к числу: а + о;
Правило прибавления числа к нулю: 0 + а;
Правило вычитания нуля из числа: а – 0;
Правило вычитания единицы из числа: а – 1;
Правило вычитания числа из самого себя: а – а ;
Правило умножения единицы на число: 1 ∙ а;
Правило умножения числа на единицу: а ∙ 1;
Правило умножения числа на ноль: а ∙ 0;
Правило деления нуля на число: 0 ∙ а;
Правило деления числа на единицу: а : 1;
Правило деления числа на само себя: а : а.
Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий. Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Выполняем вычисления.
1 ∙ 43 + 54 ∙ 0 = 43
1 ∙ 43 = 43 – по правилу умножения единицу на число
54 ∙ 0 = 54 – по правилу умножения числа на ноль
81 ∙ 1 – 0 ∙ 32 = 81
81 ∙ 1 = 81 – по правилу умножения числа на единицу
0 ∙ 32 = 0 – по правилу умножения нуля на число
(84 – 7 ∙ 12) ∙ 35 = 0
1) 7 ∙ 12 = 84, это по 7 – 12 раз, где 7 – одинаковое слагаемое, а 12 – количество одинаковых слагаемых
2) 84 – 84 = 0 – по правилу вычитания числа из самого себя
3) 0 ∙ 35 = 0, по правилу умножения нуля на число
75 ∙ (48 – 2 ∙ 24) = 0
1) 2 ∙ 24 = 48, это по 2 – 24 раза, где 2- одинаковое слагаемое, а 4 – количество одинаковых слагаемых
2) 48 – 48 = 0, по правилу вычитания числа из самого себя
3) 75 ∙ 0 = 0, по правилу умножения числа на ноль
(90 – 89) ∙ 35 = 35
1) 90 – 89 = 1
2) 1 ∙ 35 = 35, по правилу умножения единицы на число
18 ∙ (53 – 52) = 18
1) 53 – 52 = 1
2) 18 ∙ 1 = 18, по правилу умножения числа на единицу
Оформляем задание в тетрадь.
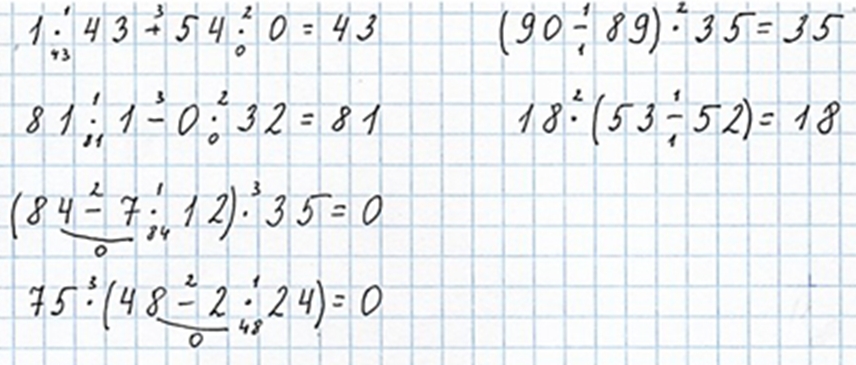
Номер 3.
Ответ:
Помни о том, что существует алгоритм объяснения умножения многозначного числа на однозначное, и будь предельно внимательным при записи такого числа, не пропускай разрядов и знаков.
1) Записываю первый множитель так, чтобы каждая цифра стояла в своей клетке. Ставлю знак умножить.
2) Записываю второй множитель так, чтобы разряд стоял под разрядом.
3) Провожу черту, обозначающую знак равно.
4) Умножение начинаю с единиц низшего разряда.
5) Умножаю десятки.
6) Умножаю сотни.
7) Аналогично умножаю все оставшиеся разряды.
8) Умножение окончено. Читаю ответ.
Выполняем умножение.
824 ∙ 9 (аналогично: 916 ∙ 3, 712 ∙ 8, 27428 ∙ 4, 15719 ∙ 5, 24845 ∙ 2)
1) записываю первый множитель так, чтобы каждая цифра стояла в своей клетке. Ставлю знак умножить;
2) записываю второй множитель так, чтобы разряд стоял под разрядом;
3) провожу черту, обозначающую знак равно;
4) умножение начинаю с единиц низшего разряда; 4 ед. ∙ 9 = 36 ед., это 3 дес. 6 ед., 6 единиц записываю в разряд единиц, а 3 дес. запоминаю.
5) умножаю десятки; 2 дес. ∙ 9 = 18 дес., это 1 сот 8 дес., да ещё 3 дес., − это 11 дес. значит, 1 дес. записываю в разряд десятков, а 2 сотни запоминаю.
6) умножаю сотни; 8 сот. ∙ 9 = 72 сот., да еще 2 сот. – 74 сот., записываю в разряд сотен
7) умножение окончено. Читаю ответ. Значение произведения от умножении 824 на 9 равно 7416.
12005 ∙ 5 (аналогично: 30704 ∙ 6, 40300 ∙ 7, 7020 ∙ 9, 7002 ∙ 9, 7200 ∙ 9)
1) записываю первый множитель так, чтобы каждая цифра стояла в своей клетке. Ставлю знак умножить;
2) записываю второй множитель. При этом запись начинаю по первой отличной от нуля цифрой.
3) провожу черту, обозначающую знак равно;
4) умножение начинаю с единиц низшего разряда; 5 ед. ∙ 5 = 25 ед., − это 2 дес. и 5 ед., значит, 5 единиц записываю под единицам, а 2 десятка запоминаю.
5) умножаю десятки; 0 дес. ∙ 5 = 0 дес. да еще 2 дес. – записываю в разряд десятков.
6) умножаю сотни; 0 сот. ∙ 5 = 0 сот., записываю в разряд сотен 0
7) умножаю тысячи; 2 тыс. ∙ 5 = 10 тыс., это 1 дес.тыс., записываю в разряд тысяч 0 и запоминаю 1 дес.тыс.
7) умножаю десятки тысяч; 1 дес.тыс. ∙ 5 = 5 дес.тыс., да ещё 1 дес.тыс., записываю в разряд десятков тысяч 6.
8) умножение окончено. Читаю ответ. Значение произведения от умножения 12 005 на 5 равно 60 025.
Оформляем задание в тетрадь.

Номер 4.
Ответ:
Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий. Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
Помни о том, что существует алгоритм письменного деления. Следуй ему, объясняя, как выполняешь деление:
1) Выделю первое неполное делимое, чтобы определить количество цифр в частном.
2) Нахожу цифру сотен в частном.
3) Нахожу, сколько сотен разделили.
4) Нахожу, сколько сотен осталось разделить.
5) Образую второе неполное делимое.
6) Нахожу, количество десятков в частном.
7) Нахожу, сколько десятков разделили.
8) Нахожу, сколько десятков осталось разделить.
9) Образую третье неполное делимое.
10) Нахожу количество единиц в частном.
11) Нахожу, сколько единиц разделили.
12) Нахожу, сколько единиц осталось разделить.
13) Читаю ответ.
Помни о том, что существует алгоритм объяснения умножения трехзначного числа на однозначное. Следуй ему:
1) Записываю первый множитель так, чтобы каждая цифра стояла в своей клетке. Ставлю знак умножить.
2) Записываю второй множитель так, чтобы разряд стоял под разрядом.
3) Провожу черту, обозначающую знак равно.
4) Умножение начинаю с единиц низшего разряда.
5) Умножаю десятки.
6) Умножаю сотни.
7) Умножение окончено. Читаю ответ.
Следуй плану при устном объяснении вычитания в столбик:
1) Записываю уменьшаемое так, чтобы каждая цифра стояла в своей клетке. Ставлю знак минус.
2) Записываю вычитаемое так, чтобы разряд стоял под разрядом.
3) Провожу черту, обозначающую знак равно.
4) Вычитание начинаю с единиц низшего разряда. Вычитаю единицы.
5) Вычитаю десятки.
6) Вычитаю сотни.
7) Вычитание окончено. Читаю ответ.
Выполняем вычисления с объяснением.
(285 + 15) : 3 ∙ 5 + 280 = 780
1) 285 + 15 = 285 + (10 + 5) = (285 + 5) + 10 = 290 + 10 = 300, по правилу прибавления суммы к числу
2) 300 : 3 = 3 сот. : 3 = 1 сот. = 100
3) 100 ∙ 5 = 1 сот. ∙ 5 = 5 сот. = 500
4) 500 + 280 = 500 + (200 + 80) = (500 + 200) + 80 = 700 + 80 = 780, по правилу прибавления суммы к числу
400 – (60 + 30) : 10 ∙ 1 = 391
1) 60 + 30 = 90
2) 90 : 10 = 9
3) 9 ∙ 1 = 9, по правилу умножения числа на единицу
4) 400 – 9 = (390 + 10) – 9 = 390 + (10 – 9) = 390 + 1 = 391, по правилу вычитания числа из суммы
(300 – 100) – 100 : (10 : 5) = 150
1) 300 – 100 = 3 сот. – 1 сот. = 2 сот. = 200
2) 10 : 5 = 2, потому что 5 ∙ 2 = 10, это по 5 – 2 раза, где 5 – одинаковое слагаемое, а 2 – количество одинаковых слагаемых
3) 100 : 2 = 1 сот. : 2 = 50
4) 200 – 50 = (100 + 100) – 50 = 100 + (100 – 50) = 100 + 50 = 150, по правилу вычитания числа из суммы
300 – (100 – 100) : (10 : 5) = 300
1) 100 – 100 = 0, по правилу вычитания числа из самого себя
2) 10 : 5 = 2, потому что 5 ∙ 2 = 10, это по 5 – 2 раза, где 5 – одинаковое слагаемое, а 2 – количество одинаковых слагаемых
3) 0 : 2 = 0, по правилу деления нуля на число
4) 300 – 0 = 300, по правилу вычитания нуля из числа
Оформляем задание в тетрадь.
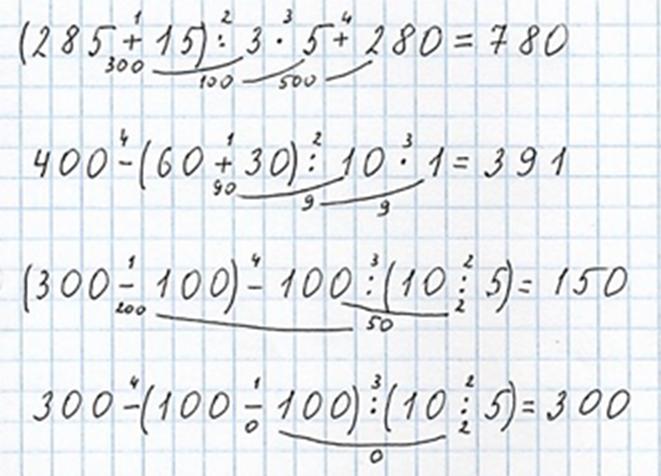
Номер 5.
Ответ:
Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий. Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Помни о том, что существует алгоритм объяснения умножения трехзначного числа на однозначное. Следуй ему:
1) Записываю первый множитель так, чтобы каждая цифра стояла в своей клетке. Ставлю знак умножить.
2) Записываю второй множитель так, чтобы разряд стоял под разрядом.
3) Провожу черту, обозначающую знак равно.
4) Умножение начинаю с единиц низшего разряда.
5) Умножаю десятки.
6) Умножаю сотни.
7) Умножение окончено. Читаю ответ.
Следуй плану при устном объяснении вычитания в столбик:
1) Записываю уменьшаемое так, чтобы каждая цифра стояла в своей клетке. Ставлю знак минус.
2) Записываю вычитаемое так, чтобы разряд стоял под разрядом.
3) Провожу черту, обозначающую знак равно.
4) Вычитание начинаю с единиц низшего разряда. Вычитаю единицы.
5) Вычитаю десятки.
6) Вычитаю сотни.
7) Вычитание окончено. Читаю ответ.
Выполняем умножение.
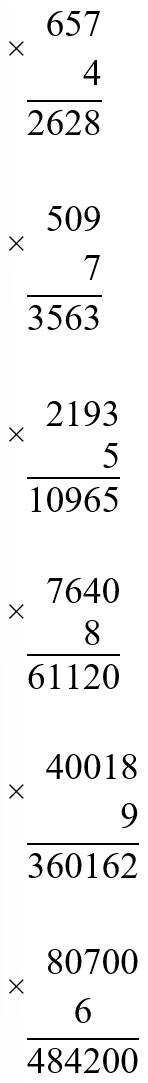
Выполняем вычисления по действиям.
(9 010 − 6 235) ∙ 9 = 24 975
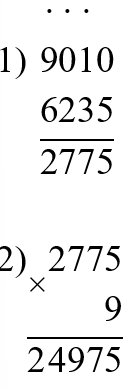
8 ∙ (4 348 + 2 062) = 51 280

Оформляем задание в тетрадь.
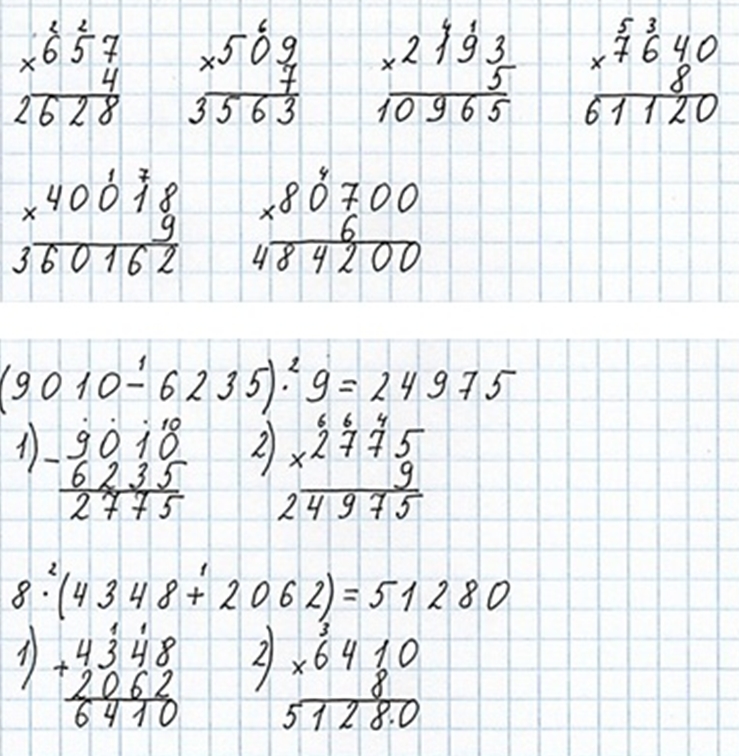
Номер 6.
Увеличь в 8 раз каждое из чисел: 700, 900, 1200. Уменьши в 7 раз каждое из чисел: 560, 98, 1400.
Ответ:700 ∙ 8 = 5600
900 ∙ 8 = 7200
1200 ∙ 8 = 9600
560 : 7 = 80
98 : 7 = 14
1400 : 7 = 200
Увеличь в 8 раз, т.е. умножь на 8, вычисляется умножением
Уменьши в 7 раз, т.е. раздели на 7, вычисляется делением
Увеличим в 8 раз каждое из чисел:
700 ∙ 8 = 5600
900 ∙ 8 = 7200
1200 ∙ 8 = 9600
Уменьшим в 7 раз каждое из чисел:
560 : 7 = 80
98 : 7 = 14
1400 : 7 = 200
Оформляем задание в тетрадь
Номер 7.
Сначала объясни, в каком из уравнений каждой пары значение х будет больше, а потом проверь вычислением.
Ответ:400 – х = 170 Значение уравнения (вычитаемое) больше, потому что разность меньше. 400 – х = 270

Х – 80 = 90 ∙ 7 Значение уравнения (уменьшаемое) больше, потому что разность больше. Х – 80 = 90 ∙ 5

Х : 6 = 56 + 44 Х : 6 = 156 + 44 Значение уравнения (делимое) больше, потому что частное больше.

Уравнение – равенство с неизвестной, при подстановке числа в которую, получается верное равенство.
Вспомни названия компонентов действия умножения, и зависимость между компонентами и результатом действия умножения:
1 множитель ∙ 2 множитель = значение произведения.
Значение произведения : 1 множитель = 2 множитель.
Значение произведения : 2 множитель = 1 множитель.
Уменьшаемое – вычитаемое = значение разности.
Уменьшаемое – значение разности = вычитаемое.
Значение разности + вычитаемое = уменьшаемое.
Делимое : делитель = значение разности.
Делимое : значение разности = делитель.
Значение разности ∙ делитель = делимое
Выполняем вычисления с объяснением первой пары уравнений.
В данном уравнении – 400 – х = 170 значение уравнения (вычитаемое) больше, потому что разность меньше, чем в 400 – х = 270.
400 – х = 170
х = 400 – 170
х = 230
Проверка:
400 – 230 = 170
170 = 170
400 – х = 270
х = 400 – 270
х = 130
Проверка:
400 – 130 = 270
270 = 270
Выполняем вычисления с объяснением второй пары уравнений.
В данном уравнении - х – 80 = 90 ∙ 7 значение уравнения (уменьшаемое) больше, потому что разность больше, чем в х – 80 = 90 ∙ 5.
х – 80 = 90 ∙ 7
х – 80 = 630
х = 630 + 80
х = 710
Проверка:
710 – 80 = 90 ∙ 7
630 = 630
х – 80 = 90 ∙ 5
х – 80 = 450
х = 450 + 80
х = 530
Проверка:
530 – 80 = 90 ∙ 5
450 = 450
Выполняем вычисления с объяснением третьей пары уравнений.
В данном уравнении – х : 6 = 156 + 44 значение уравнения (делимое) больше, потому что частное больше, чем в х : 6 = 56 + 44.
х : 6 = 56 + 44
х : 6 = 100
х = 100 ∙ 6
х = 600
Проверка:
600 : 6 = 56 + 44
100 = 100
х : 6 = 156 + 44
х : 6 = 200
х = 200 ∙ 6
х = 1 200
Проверка:
1 200 : 6 = 156 + 44
200 = 200
Оформляем задание в тетрадь.
Номер 8.
Выполни деление с остатком и проверь.
Ответ:



Вспомни названия компонентов действия деления и зависимость между компонентами и результатами действия деления:
Делимое : делитель = значение частного.
Проверка:
Значение частного ∙ делитель = делимое.
Делимое : значение частного = делитель.
Рассуждаем
При проверке деления с остатком:
1) смотрим, чтобы остаток был меньше делителя;
2) выполняем умножение частного на делитель;
3) к полученному результату прибавляем остаток.
Если последнее число равно делимому, то деление выполнено верно.
Выполняем вычисления и оформляем задание в тетрадь.
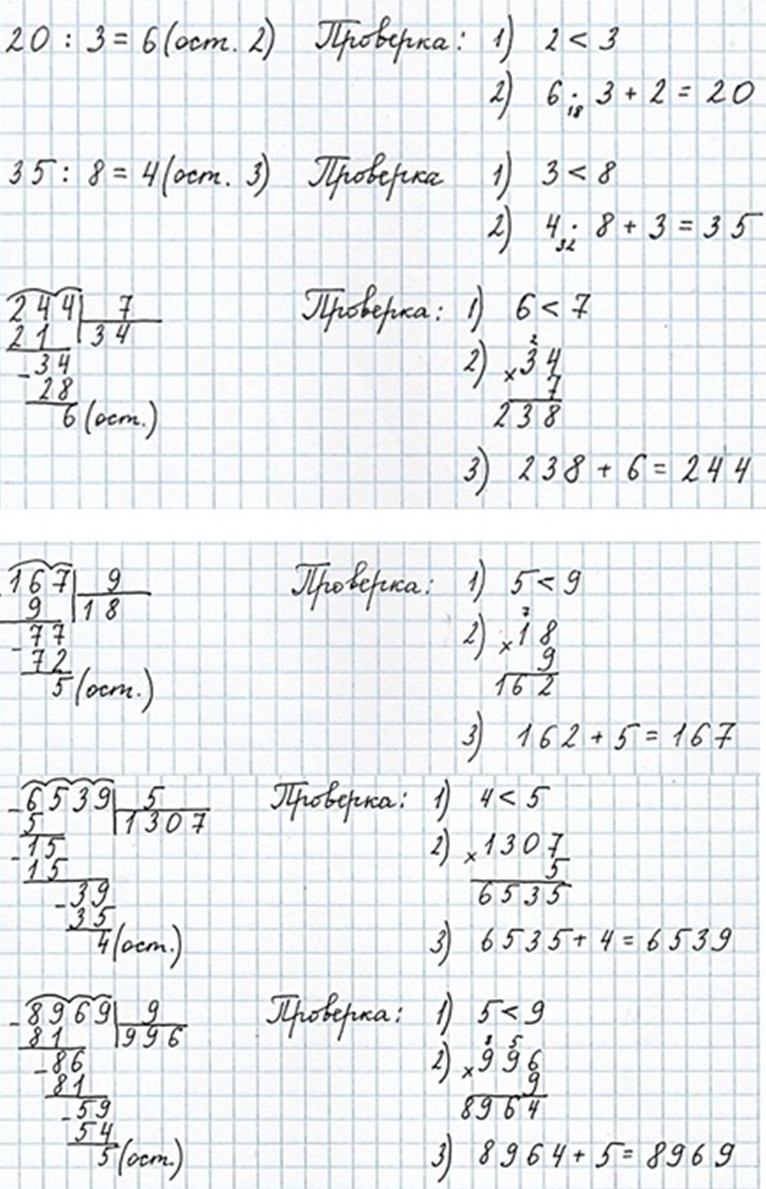

Номер 9.
Вычисли и сделай проверку.
Ответ:
Помни о том, что существует алгоритм письменного деления. Следуй ему, объясняя, как выполняешь деление:
1) Выделю первое неполное делимое, чтобы определить количество цифр в частном.
2) Нахожу цифру сотен в частном.
3) Нахожу, сколько сотен разделили.
4) Нахожу, сколько сотен осталось разделить.
5) Образую второе неполное делимое.
6) Нахожу, количество десятков в частном.
7) Нахожу, сколько десятков разделили.
8) Нахожу, сколько десятков осталось разделить.
9) Образую третье неполное делимое.
10) Нахожу количество единиц в частном.
11) Нахожу, сколько единиц разделили.
12) Нахожу, сколько единиц осталось разделить.
13) Читаю ответ.
Помни о названии компонентов действия деления и зависимости между компонентами и результатом действия деления:
Делимое : делитель = значение частного.
Делимое : значение частного = делитель.
Значение частного ∙ делитель = делимое.
Выполняем вычисления с пояснениями.
Пишем: 7 410 : 3.
Делим тысячи: 7 тыс. – это первое неполное делимое. Значит, в частном получатся тысячи и в записи частного будет 4 цифры.
Разделим 7 на 3, получим 2 – столько тысяч будет в частном.
Умножим 2 на 3, получим 6 – столько тысяч разделили.
Вычтем 6 из 7, получим 1 – столько тысяч осталось разделить.
Сравним остаток с делителем: число оставшихся тысяч меньше, чем 3.
Делим сотни.
1 тыс. и 4 сот., всего 14 сот. Это – второе неполное делимое.
Разделим 14 на 3, получим 4 – столько сотен будет в частном.
Умножим 4 на 3, получим 12 – столько сотен разделили.
Вычтем 12 из 14, получим 2 – столько сотен осталось разделить.
Сравним остаток с делителем: число оставшихся сотен меньше, чем 3.
Делим десятки.
2 сот. 1 дес., всего 21 дес. Это – третье неполное делимое.
Разделим 21 на 3, получим 7 – столько десятков будет в частном.
Умножим 7 на 3, получим 21 – столько десятков разделили.
Вычтем 21 из 21, получим 0 – десятки разделили все.
Делим единицы.
0 разделим на 3 получим 0 единиц в частном.
Читаем ответ: 2 470.
Далее рассуждаем аналогично.
Выполняем проверку.

Номер 10.
Ответ:
Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий. Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
Помни о том, что существует алгоритм письменного деления. Следуй ему, объясняя, как выполняешь деление:
1) Выделю первое неполное делимое, чтобы определить количество цифр в частном.
2) Нахожу цифру сотен в частном.
3) Нахожу, сколько сотен разделили.
4) Нахожу, сколько сотен осталось разделить.
5) Образую второе неполное делимое.
6) Нахожу, количество десятков в частном.
7) Нахожу, сколько десятков разделили.
8) Нахожу, сколько десятков осталось разделить.
9) Образую третье неполное делимое.
10) Нахожу количество единиц в частном.
11) Нахожу, сколько единиц разделили.
12) Нахожу, сколько единиц осталось разделить.
13) Читаю ответ.
Помни о том, что существует алгоритм объяснения умножения трехзначного числа на однозначное. Следуй ему:
1) Записываю первый множитель так, чтобы каждая цифра стояла в своей клетке. Ставлю знак умножить.
2) Записываю второй множитель так, чтобы разряд стоял под разрядом.
3) Провожу черту, обозначающую знак равно.
4) Умножение начинаю с единиц низшего разряда.
5) Умножаю десятки.
6) Умножаю сотни.
7) Умножение окончено. Читаю ответ.
Следуй плану при устном объяснении вычитания в столбик:
1) Записываю уменьшаемое так, чтобы каждая цифра стояла в своей клетке. Ставлю знак минус.
2) Записываю вычитаемое так, чтобы разряд стоял под разрядом.
3) Провожу черту, обозначающую знак равно.
4) Вычитание начинаю с единиц низшего разряда. Вычитаю единицы.
5) Вычитаю десятки.
6) Вычитаю сотни.
7) Вычитание окончено. Читаю ответ.
Выполняем вычисления.
200 000 − 160 032 : 8 = 179 996
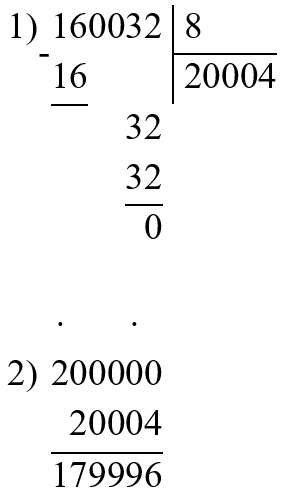
900 000 − 54 027 : 9 = 893 997

200 000 − 521 160 : 4 = 69 710
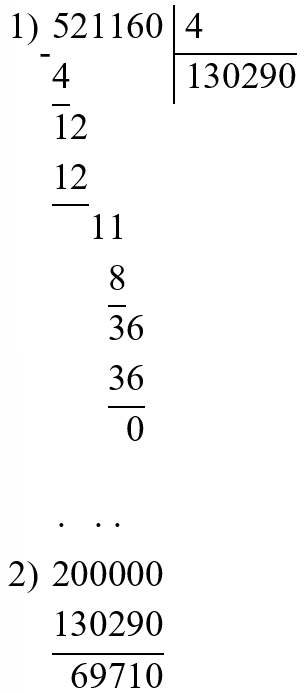
400 000 − 81 270 : 3 = 372 910
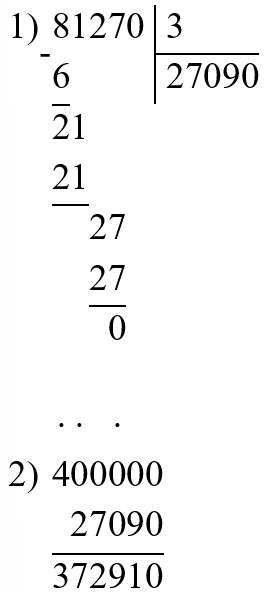
Выполняем проверку.
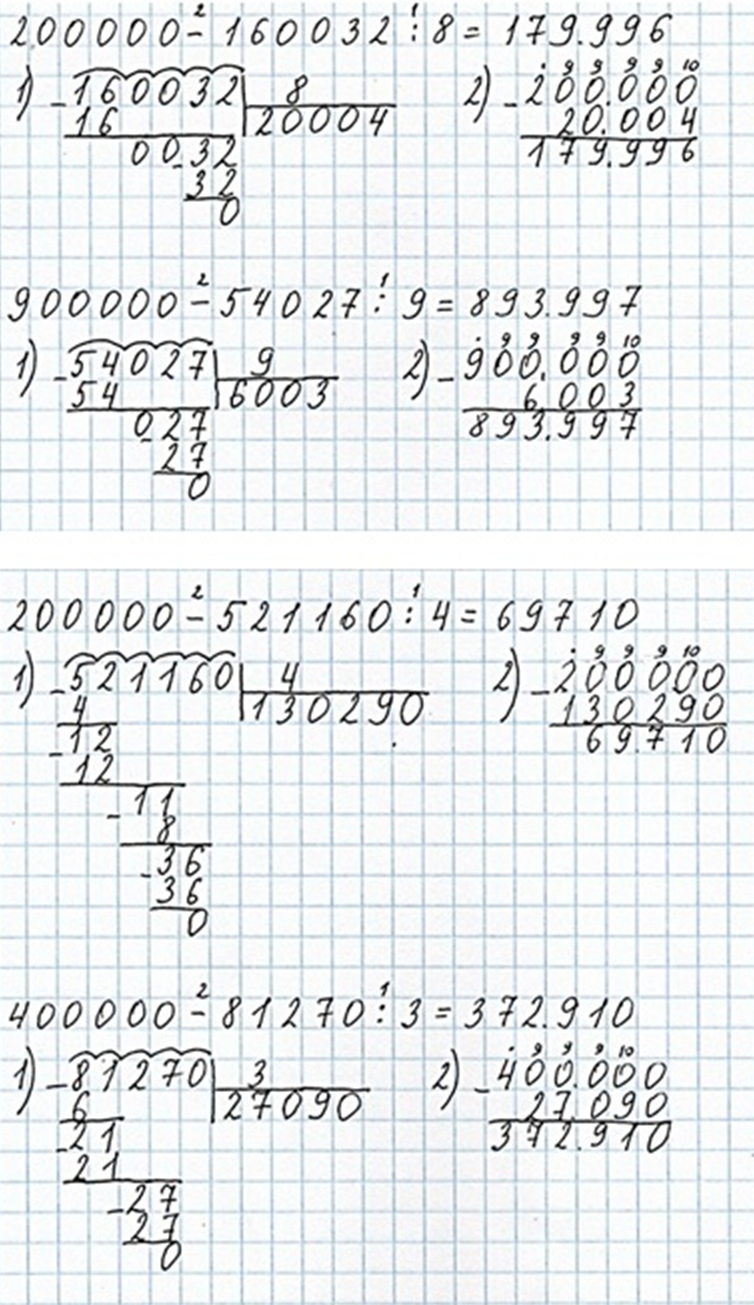
Номер 11.
Объясни, почему неравенства верны.
Ответ:170 ∙ 5 + 8 ∙ 5 > 169 ∙ 5 + 6 ∙ 5
Умножение – это многократное повторение одного слагаемого. С левой стороны число 5 сначала повторили 170 раз, затем еще 8 раз. Значит всего 178 раза. Справа число 5 повторили сначала 169 раз, затем еще 6 раза. Значит всего 175 раз. Поэтому неравенство верно.
6102 ∙ (81 : 81) > 6102 ∙ (81 - 81)
С левой стороны в скобках получается 1. Общий результат 6102. С правой стороны в скобках получается 0. Общий результат 0. Поэтому неравенство верно.
676 : 4 < 676 : 2
Делимое одинаково, но с левой стороны делитель больше, поэтому результат частного будет меньше.
359 ∙ 4 > 359 ∙ 3
Первые множители равны, но второй множитель с левой стороны больше, поэтому и результат произведения будет больше.
Для того, чтобы понять верны равенства или нет – необходимо вычислить значения выражений обеих частей, но для начала – проанализировать их.
Объясним, почему неравенства верны.
170 ∙ 5 + 8 ∙ 5 > 169 ∙ 5 + 6 ∙ 5
Умножение – это многократное повторение одного слагаемого. С левой стороны число 5 сначала повторили 170 раз, затем еще 8 раз. Значит всего 178 раза. Справа число 5 повторили сначала 169 раз, затем еще 6 раза. Значит всего 175 раз. Поэтому неравенство верно.
6102 ∙ (81 : 81) > 6102 ∙ (81 – 81)
С левой стороны в скобках получается 1. Общий результат 6102. С правой стороны в скобках получается 0. Общий результат 0. Поэтому неравенство верно.
676 : 4 < 676 : 2
Делимое одинаково, но с левой стороны делитель больше, поэтому результат частного будет меньше.
359 ∙ 4 > 359 ∙ 3
Первые множители равны, но второй множитель с левой стороны больше, поэтому и результат произведения будет больше.
Оформим задание в тетрадь.
170 ∙ 5 + 8 ∙ 5 > 169 ∙ 5 + 6 ∙ 5
(170 + 8) ∙ 5 > (169 + 6) ∙ 5
178 ∙ 5 > 175 ∙ 5
178 > 175
6102 ∙ (81 : 81) > 6102 ∙ (81 – 81)
6102 ∙ 1 > 6102 ∙ 0
1 > 0
676 : 4 < 676 : 2
359 ∙ 4 > 359 ∙ 3
Задание на полях страницы
Ребус.

3542 : 7 = 506
Помни о названии компонентов действия деления и зависимости между компонентами и результатом действия деления:
Делимое : делитель = значение частного.
Делимое : значение частного = делитель.
Значение частного ∙ делитель = делимое.
Помни о том, что существует алгоритм письменного деления. Следуй ему, объясняя, как выполняешь деление:
1) Выделю первое неполное делимое, чтобы определить количество цифр в частном.
2) Нахожу цифру сотен в частном.
3) Нахожу, сколько сотен разделили.
4) Нахожу, сколько сотен осталось разделить.
5) Образую второе неполное делимое.
6) Нахожу, количество десятков в частном.
7) Нахожу, сколько десятков разделили.
8) Нахожу, сколько десятков осталось разделить.
9) Образую третье неполное делимое.
10) Нахожу количество единиц в частном.
11) Нахожу, сколько единиц разделили.
12) Нахожу, сколько единиц осталось разделить.
13) Читаю ответ.
Рассмотрим ребус на полях и решим его.

Делитель неизвестен, а в значении частного 3 знака, значит, что неполных делимых было 2, но по сокращенному способу их было всего 2.
Первое неполное делимое неизвестно. Десятков в нем 3, а количество сотен в значении частного − 5. При этом первое неполное делимое такое, что при вычитании из него числа получился нулевой остаток, а количество сотен равно 5. Нужно вспомнить, какое число делится на 5 без остатка.
Это число 35, потому что 5 сот. ∙ 7 − 35 сот., значит, что в делимом 5 сотен, а делитель − 7.
При этом количество десятков в делителе равно нулю.
Второе неполное делимое - неизвестно, но в нем 4 десятка. Значит, необходимо вспомнить, какое число пятого десятка без остатка делится на 7. Это число 42 или 49. Значит, в значении частного может быть 6 единиц или 7 единиц.
Тогда, получаем 2 равенства:
1. 3 549 : 7 = 507
2. 3 542 : 7 = 506
Оформим задание в тетрадь.
1. 3 549 : 7 = 507
2. 3 542 : 7 = 506
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.