ГДЗ по математике 4 класс учебник Моро, Бантова 1 часть

Первые весы – бытовые (граммы); Вторые весы – торговые или товарные (кг); Третьи весы – для большого груза (центнеры или тонны).

Подсказка:

Весы – это прибор, специальное устройство для измерения такой величины предмета, как масса.
Масса – величина предмета, которая может выражаться в граммах, килограммах, центнерах и тонных.
Но существуют разные виды весов в зависимости от того, для измерения массы чего они используются.

Шаг 1.
Рассмотрим рисунки.

Шаг 2.
Сделаем вывод.

Первые весы – бытовые (граммы);
Вторые весы – торговые или товарные (кг);
Третьи весы – для большого груза (центнеры или тонны).

1 ц = 100 кг 100 : 50 = 2 (м.) – потребуется.
Ответ: 2 мешка всего потребуется для 1 ц картофеля.

Подсказка:

Помним конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а · 3, а – первый множитель, а 3 – количество множителей.
Помним о зависимости между компонентами и результатом действия умножения:

   1 множитель · 2 множитель = значение произведения.
   Значение произведения : 1 множитель = 2 множитель.
   Значение произведения : 2 множитель = 1 множитель.

Данная задача характеризуется зависимостями между компонентами:

   Масса 1 мешка · количество мешков = общая масса картофеля.
   Общая масса картофеля : масса 1 мешка = количество мешков.
   Общая масса картофеля : количество мешков = масса 1 мешка.

В условии задачи дана подсказка: «вырази 1 ц. в килограммах».

Шаг 1.
Оформляем условие в виде таблицы.

Шаг 2.
Рассуждаем.

В одном центнере 100 кг. При этом в 1 мешке 50 кг картофеля. 50 кг – это половина 100 кг, значит, чтобы понять, сколько мешков потребуется для картофеля, нужно общее количество картофеля (1 ц) разделить на вместимость одного мешка.
1 ц = 100 кг.

Шаг 3.
Продолжаем рассуждение.

Общая масса картофеля складывается из массы картофеля каждого мешка. Значит, чтобы узнать, сколько мешков потребовалось для картофеля, нужно общее количество картофеля разделить на массу 1 мешка.
100 : 50 = 2 (м.) – потребуется.

Шаг 4.
Записываем ответ.

Ответ: 2 мешка.

Всего – 1275 кг. Груз – 275 кг. Автомобиль – ? кг. 1275 – 275 = 1000 (кг). 1000 кг = 1 т.
Ответ: масса самого автомобиля составляет 1 т.

Подсказка:

Помни о зависимости между частью и целым:

часть + часть = целое.
целое – 1 часть = 2 часть.
целое – 2 часть = 1 часть.

Шаг 1.
Оформляем условие в виде краткой записи.

Всего – 1275 кг.
Груз – 275 кг.
Автомобиль – ? кг.

Шаг 2.
Рассуждаем.

Масса нагруженного автомобиля складывается из массы машины и груза. Значит, чтобы узнать, чему равна масса машины, нужно из общей массы машины с грузом вычесть массу груза.
1275 – 275 = 1000 (кг).
1000 кг = 1 т.

Шаг 3.
Записываем ответ.

Ответ: 1 т масса автомобиля.

1) 3 ц = 300 кг. 8 ц = 800 кг. 10 ц = 1000 кг. 2 т = 2000 кг.
2) 1 т = 10 ц. 1 т 5 ц = 15 ц. 200 кг = 2 ц.
3) 1000000 г = 1000 кг = 1 т – нельзя поднять.

Подсказка:

Масса – величина предмета, которая может выражаться в граммах, килограммах, центнерах и тонных.
Помним о соотношении числовых значений единиц измерения массы:

1 кг = 1000 г.
1 ц = 100 кг.
1 т = 1000 кг.

Шаг 1.
Переведём в кг.

3 ц; 1 ц = 100 кг, значит, 3 · 100 = 300 кг.
8 ц; 1 ц = 100 кг, значит, 8 · 100 = 800 кг.
10 ц; 1 ц = 100 кг, значит, 10 · 100 = 1 000 кг.
2 т; 1 т = 1 000 кг, значит, 2 · 1 000 = 2 000 кг.

Шаг 2.
Переведём в ц.

1 т; 1 т = 1000 кг, 1 ц = 100 кг, значит, 1000 : 100 = 10 ц. 1 т 5 ц; 1 т = 1000 кг, 1 ц = 100 кг, значит, 1000 : 100 = 10 ц да еще 5 ц = 15 ц. 200 кг; 100 кг = 1 ц, значит, 200 : 100 = 2 ц.

Шаг 3.
Рассуждаем и отвечаем на вопрос.

«Можешь ли ты поднять?»
1 000 000 г – непонятно много это или мало, тяжело или невесомо. Поэтому, выражу эту величину в более крупных единицах:
1 кг – 1 000 г, значит, 1 000 000 : 1 000 = 1 000 кг, а 1 000 кг = 1 т, значит, я не смогу поднять груз в 1 тонну, ведь столько весит, например, легковая машина.

Сколько парников занято огурцами?

математика 4 класс Моро, Бантова - 1 часть страница 45, номер 204

1) 100 : 5 = 20 (п) – луком. 2) 20 : 2 = 10 (п) – салатом. 3) 20 + 10 = 30 (п) – вместе с луком и салатом. 4) 100 – 30 = 70 (п) – всего
Ответ: 70 парников всего занято огурцами.

Подсказка:

«в 2 раза меньше», значит, вычисляется делением.
Доля – одна часть из тех, на которые разделили целое. Например, если целое разделили на 5 частей, то доля – это одна пятая, т.е. одна часть из пяти.
Первое слово в названии долей указывает на количество долей, которые взяли, а второе – на сколько частей разделили целое.

Шаг 1.
Оформляем условие в виде краткой записи и поставим вопрос.

Сколько парников занято огурцами?

Шаг 2.
Рассуждаем.

Всего – 100 парников. Пятая часть от них занята луком. Пятая, значит, что луком занято в 5 раз меньше парников, чем их есть всего. Значит, чтобы узнать, сколько парников занято луком, нужно общее количество парников разделить на 5.
1) 100 : 5 = 20 (п.) – луком.

Шаг 3.
Продолжаем рассуждение.

Салатом занято в 2 раза меньше, чем луком. Значит, чтобы узнать, сколько парников занято салатом, нужно количество парников разделить на 2.
2) 20 : 2 = 10 (п.) – салатом.

Шаг 4.
Продолжаем рассуждение.

Общее количество занятых парников складывается из количества парников, занятых луком и салатом. Значит, чтобы узнать, сколько парников занято, складываем количество парников каждого вида.
3) 20 + 10 = 30 (п.) – вместе с луком и салатом.

Шаг 5.
Продолжаем рассуждение.

Общее количество парников складывается из тех, что нам известны и тех, что заняты огурцами. Значит, чтобы узнать, сколько парников занято огурцами, из общего количество парников вычитаю сумму количества парников с луком и салатом.
4) 100 − 30 = 70 (п.).

Шаг 6.
Записываем ответ.

Ответ: 70 парников с огурцами.
Решение выражением: 100 – ((100 : 5) + ((100 : 5) : 2)) = 70 (п.).

математика 4 класс Моро, Бантова - 1 часть страница 45, номер 205

61000 − 1 = 60999 49099 + 1 = 49100

Подсказка:

а + 1 – прибавить единицу, т.е. увеличить на 1, вычисляется сложением.
а – 1 – вычесть единицу, т.е. уменьшить на 1, вычисляется вычитанием.
а : 10 – значит, уменьшить в 10 раз, разделить на 10, вычисляется делением.
а · 10, значит, увеличить в 10 раз, умножить на 10, вычисляется умножением.
а · 1 000, значит, увеличить в 1 000 раз, умножить на 1 000, умножение.
а : 100, значит, уменьшить в 100 раз, разделить на 100, вычисляется делением.

Помним о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.

Шаг 1.
Расставляем порядок действий и выполняем вычисления.

Шаг 2.
Выполняем вычитание и сложение.

61000 – 1 = 60999
49099 + 1 = 49100

математика 4 класс Моро, Бантова - 1 часть страница 45, номер 206

Подсказка:

Помним о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Помним алгоритм объяснения умножения трехзначного числа на однозначное:

1) Записываю первый множитель так, чтобы каждая цифра стояла в своей клетке. Ставлю знак умножить;
2) Записываю второй множитель так, чтобы разряд стоял под разрядом;
3) Провожу черту, обозначающую знак равно;
4) Умножение начинаю с единиц низшего разряда;
5) Умножаю десятки;
6) Умножаю сотни;
7) Умножение окончено. Читаю ответ.

Следуйте плану при устном объяснении вычитания в столбик:

1) Записываю уменьшаемое так, чтобы каждая цифра стояла в своей клетке. Ставлю знак минус;
2) Записываю вычитаемое так, чтобы разряд стоял под разрядом;
3) Провожу черту, обозначающую знак равно;
4) Вычитание начинаю с единиц низшего разряда. Вычитаю единицы;
5) Вычитаю десятки;
6) Вычитаю сотни;
7) Вычитание окончено. Читаю ответ.

Помним алгоритм письменного деления:

1) Выделю первое неполное делимое, чтобы определить количество цифр в частном.
2) Нахожу цифру сотен в частном:
3) Нахожу, сколько сотен разделили:
4) Нахожу, сколько сотен осталось разделить:
5) Образую второе неполное делимое:
6) Нахожу, количество десятков в частном:
7) Нахожу, сколько десятков разделили:
8) Нахожу, сколько десятков осталось разделить:
9) Образую третье неполное делимое:
10) Нахожу количество единиц в частном:
11) Нахожу, сколько единиц разделили:
12) Нахожу, сколько единиц осталось разделить:
13) Читаю ответ.

Шаг 1.
Расставляем порядок действий и выполняем вычисления.

(987 – 879) · 6 = 648

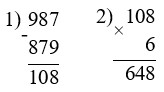
900 – 139 · 5 = 205

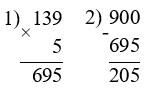
2 · (293 + 62) = 710

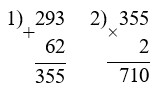
4 · 197 – 189 = 599

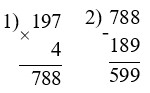
3 · 242 + 824 : 4 = 932

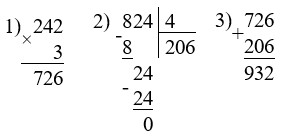
(4 · 209 – 228) : 8 = 76

Шаг 2.
Оформляем задание в тетрадь.

а = 4 см S = 36 см² P = ? см Р = (а + b) ∙ 2 S = a ∙ b b = S : a b = 36 : 4 b = 9 см P = (9 + 4) ∙ 2 P = 26 см
Ответ: Р = 26 см.
Можно оформить так:
Сторона – 4 см S = 36 см² Р = ? см 1) 36 : 4 = 9 (см) – длина другой стороны. 2) (9 + 4) ∙ 2 = 26 (см)
Ответ: Р = 26 см

Подсказка:

Периметр – сумма длин всех сторон. Чтобы узнать, чему равен периметр прямоугольника нужно измерить длины всех сторон, а полученные значения сложить.
Сделать это можно тремя способами:

1) (а + в) · 2
2) а · 2 + в · 2
3) а + в + а + в

Площадь фигуры – часть плоскости, занятая фигурой. Площадь может измеряться в единицах измерения: мм², см², дм², м², км² и др.
Площадь прямоугольника – произведение длин его сторон. Вычисляется по формуле: а · в, где а и в – стороны прямоугольника.

Шаг 1.
Оформляем условие.

а = 4 см.
S = 36 см².
P = ? см.

Шаг 2.
Рассуждаем.

Мы знаем, чтобы S = a ∙ b, следовательно, чтобы найти другую сторону нужно площадь разделить на известную сторону.
b = S : a.
b = 36 : 4.
b = 9 см.

Шаг 3.
Продолжаем рассуждение.

Теперь, когда мы знаем длину и ширину, можем найти периметр.
Р = (а + b) ∙ 2.
P = (9 + 4) ∙ 2.
P = 26 см.

Шаг 4.
Записываем ответ.

Ответ: Р = 26 см.

1 взвешивание: Используя гирю в 100 г отвесим 100 г крупы. Получили 100г.
2 взвешивание: Используя гирю в 100 г и имеющиеся 100 г крупы поставим их рядом на одну чашу весов и отвесим 200 г крупы. Получили уже: 100 + 200 = 300 г.
3 взвешивание: Используя гирю в 100 г и имеющиеся 300 г крупы поставим их рядом на одну чашу весов и отвесим 400 г крупы. Получили: 300 + 400 = 700 г.

Подсказка:

Весы – это прибор, специальное устройство для измерения такой величины предмета, как масса.
Масса – величина предмета, которая может выражаться в граммах, килограммах, центнерах и тонных.
Помним, что чаши весов могут многое рассказать о том, какова масса предметов, расположенных на чашах:
Если чаша расположена выше, то масса предмета на ней меньше.
Если чаша распложена ниже, то масса предмета на ней больше.
Если чаши находятся на одном уровне, то масса предметов на них одинакова.

Шаг 1.
Рассуждаем.

Нам дана только одна гиря массой 100г. Таким образом при взвешивание будем использовать гирю и уже взвешенную крупу.

Шаг 2.
Первое взвешивание.

Используем гирю в 100 г и отвесим 100 г крупы. Получили 100г.

Шаг 3.
Второе взвешивание.

Используем гирю в 100 г и имеющиеся 100 г крупы поставим их рядом на одну чашу весов и отвесим 200 г крупы.
Получаем: 100 + 200 = 300 г.

Шаг 4.
Третье взвешивание.

Используем гирю в 100 г и имеющиеся 300 г крупы поставим их рядом на одну чашу весов и отвесим 400 г крупы.
Получаем: 300 + 400 = 700 г.

7 т 500 кг = 75 ц – масса африканского слона. 4 т = 40 ц – масса бегемота.

Подсказка:

Масса – величина предмета, которая может выражаться в граммах, килограммах, центнерах и тонных.
Помним о соотношении числовых значений единиц измерения массы:

1 кг = 1000 г.
1 ц = 100 кг.
1 т = 1000 кг.

Шаг 1.
Оформляем условие.

Вес слона – 7 т 500 кг.
Вес бегемота – 4 т.

Шаг 2.
Рассуждаем.

Если 1 т – 1000 кг, то 7 · 1000 = 7000 кг да еще 500 кг – 7 500 кг.
Мы знаем, что 1 ц – 100 кг, значит, 7500 : 100 = 75 ц. – масса африканского слона.

Шаг 3.
Продолжаем рассуждение.

Если 1 т – 1000 кг, а 100 кг – 1 ц, значит, 1000 кг : 100 = 10 ц – 1 т. Получается, 4 · 10 = 40ц – масса бегемота.

Математика 4 класс учебник Моро, Бантова 1 часть ответы – страница 45

Единицы массы

Единицы массы