Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 96
- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Геометрические фигуры
Номер 1.
Назови знакомые тебе геометрические фигуры, начерти их в тетради и обозначь буквами.
Ответ:
Повтори материал о треугольнике, круге, окружности, многоугольнике, угле, отрезке, луче, прямой и ломаной.
Начертим геометрические фигуры в тетради.
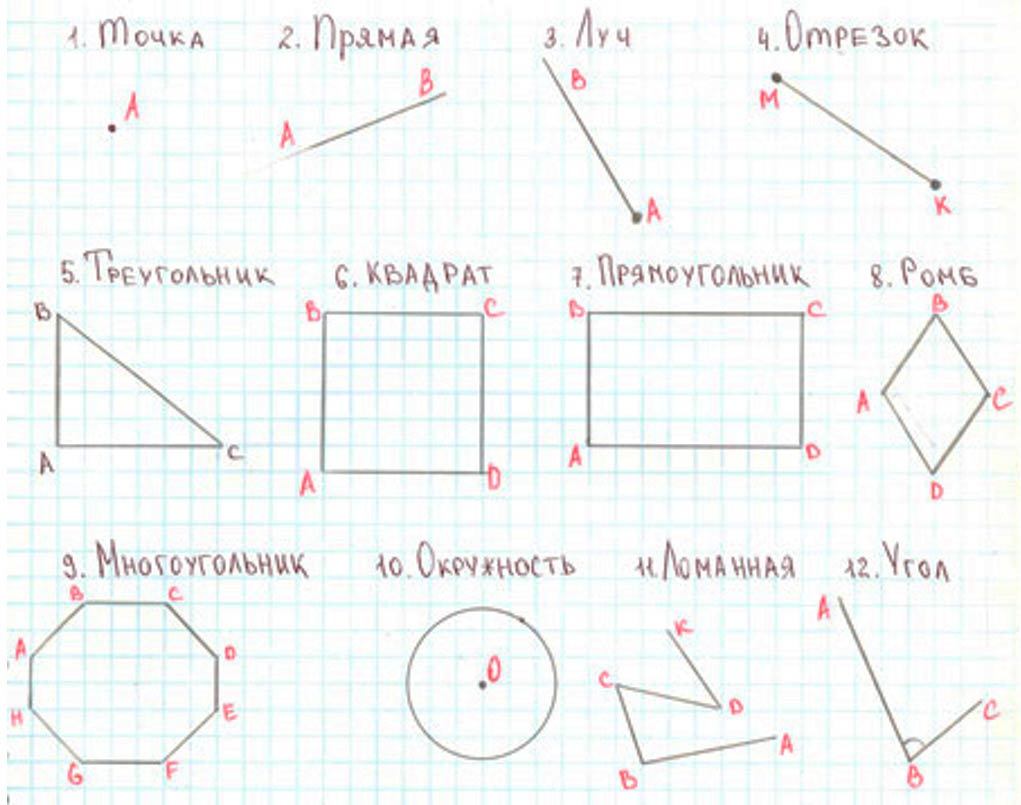
Назовем знакомые фигуры.
Точка (А), отрезок (МК), прямая (АВ), луч (А), треугольник (ABC), квадрат (ABCD), прямоугольник (АВСD), многоугольник (ABCDEFGH), окружность (круг), ломаная (KDCBA), угол (АВС).
Оформим задание в тетрадь.
Номер 2.
Что ты знаешь о многоугольниках? Сколько вершин, углов и сторон у двенадцатиугольника?
Ответ:Многоугольник это плоская замкнутая ломаная без самопересечений. Вершины ломаной называются вершинами многоугольника, а её звенья — сторонами многоугольника. Многоугольники называются по количеству углов-3 угла это треугольник, 4 угла это четырехугольник и т.д. В любом многоугольнике число углов равно числу сторон и вершин. В двенадцатиугольнике 12 углов, 12 вершин и 12 сторон.
Повтори, какие бывают многоугольники.
Расскажем, что мы знаем о многоугольниках.
Многоугольник это плоская замкнутая ломаная без самопересечений. Вершины ломаной называются вершинами многоугольника, а её звенья – сторонами многоугольника.
Многоугольники называются по количеству углов – 3 угла это треугольник, 4 угла это четырехугольник и т.д.
В любом многоугольнике число углов равно числу сторон и вершин.
Охарактеризуем двенадцатиугольник.
В двенадцатиугольнике 12 углов, 12 вершин и 12 сторон.
Номер 3.
Какие виды треугольников ты знаешь? Может ли прямоугольный треугольник быть равносторонним? разносторонним? Может ли тупоугольный треугольник быть равнобедренным? Начерти в тетради равнобедренный прямоугольный треугольник.
Ответ:
Повтори, какие бывают треугольники.
Расскажем, какие виды треугольников мы знаем.
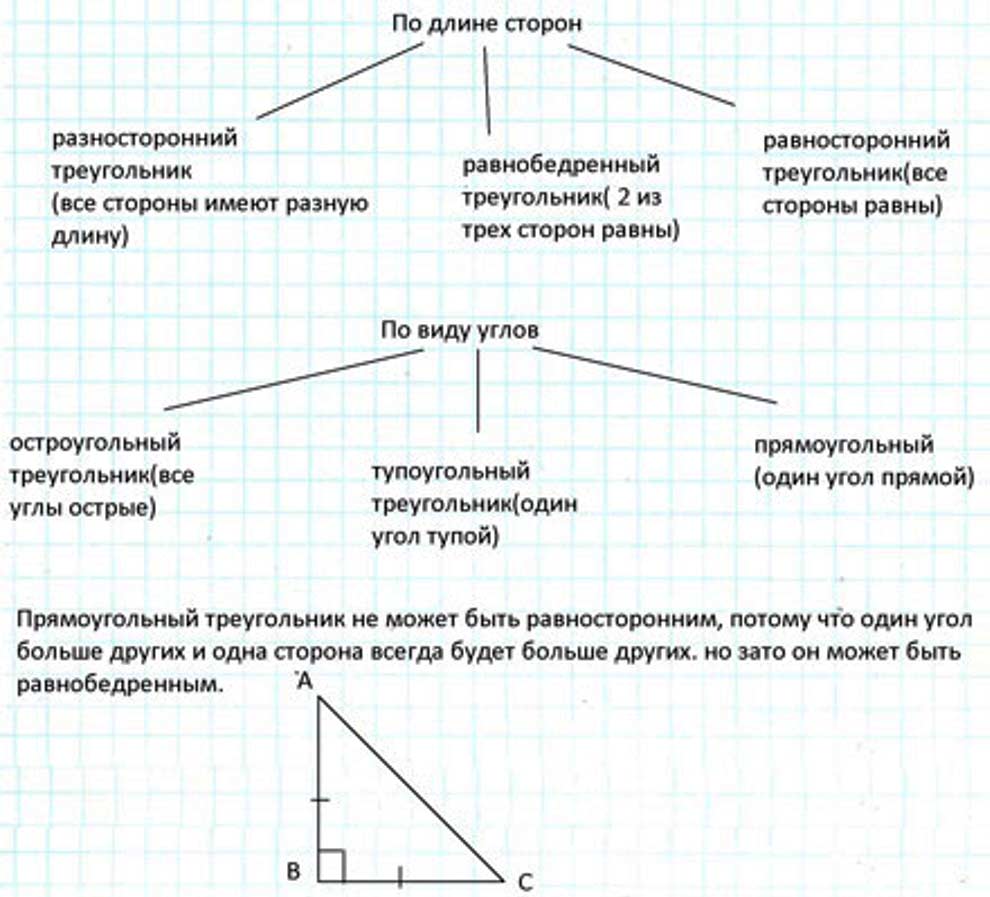
По длине сторон: разносторонний треугольник (все стороны имеют разную длину); равнобедренный треугольник (2 из трех сторон равны); равносторонний треугольник (все стороны равны).
По виду углов: остроугольный треугольник (все углы острые); тупоугольный треугольник (один угол тупой); прямоугольный (один угол прямой).
Прямоугольный треугольник не может быть равносторонним, потому что один угол больше других и одна сторона всегда будет больше других, но зато он может быть равнобедренным.
Оформим задание в тетрадь.
Номер 4.
Какие виды четырёхугольников ты знаешь? Продолжи предложения:
Ответ:
Виды четырехугольников: прямоугольник, квадрат, ромб.
1) Прямоугольник – это четырехугольник, у которого все углы прямые.
2) Квадрат – это прямоугольник, у которого все стороны равны.
Повтори, какие бывают четырёхугольники.
Продолжим предложения.
Виды четырехугольников: прямоугольник, квадрат, ромб.
1) Прямоугольник – это четырехугольник, у которого все углы прямые.
2) Квадрат – это прямоугольник, у которого все стороны равны.
Оформим задание в тетрадь.
Номер 5.
1) Среди четырёхугольников, изображённых на рисунке 1, найди прямоугольники и запиши их названия; подчеркни название квадрата.
2) Найди периметр прямоугольника ОРКС и площадь квадрата. Объясни, почему четырёхугольник ABCD нельзя назвать квадратом.
Ответ:
2) Периметр ОРКС = (15 мм + 9 мм) ∙ 2 = 30 мм + 18 мм = 48 мм = 4 см 8 мм.
Площадь FKME = 9 мм ∙ 9 мм = 81 мм².
Прямоугольник АBCD нельзя назвать квадратом, потому что квадрат-прямоугольник, а у прямоугольника углы прямые. В ромбе ABCD углы не прямые.
Повтори, какие бывают многоугольники, как найти площадь и периметр прямоугольника.
Рассмотрим геометрические фигуры на полях страницы.
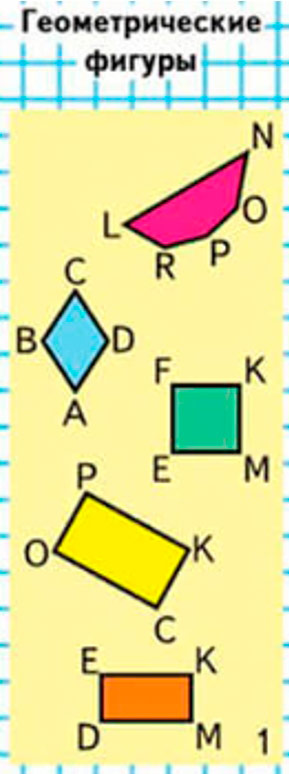
Найдем прямоугольники и запишем их названия.
Прямоугольники: ОРКС, FKME, EKMD.
Найдем периметр прямоугольника и площадь квадрата.
Периметр ОРКС = (15 мм + 9 мм) ∙ 2 = 30 мм + 18 мм = 48 мм = 4 см 8 мм.
Площадь FEKM = 9 мм ∙ 9 мм = 81 м².
Прямоугольник АBCD нельзя назвать квадратом, потому что квадрат – прямоугольник, а у прямоугольника углы прямые. В ромбе ABCD углы не прямые.
Номер 6.
Определи вид каждого треугольника, если его периметр находят так: 1) 3 + 4 + 5 = 12 (см); 2) 3 ∙ 2 + 4 = 10 (см); 3) 5 ∙ 3 = 15 (см).
Ответ:1) Так находят периметр разностороннего треугольника, ведь он имеет разные длины сторон. В данном случае 3, 4 и 5. 2) Так находят периметр равнобедренного треугольника, ведь две его стороны равны (умножением нашли их сумму) и прибавили 4 - длина третьей стороны. 3) Так находят периметр равностороннего треугольника, стороны которого равны.
Повтори, какие бывают треугольники и как найти периметр многоугольника.
Определим вид каждого треугольника по нахождению периметра.
1) Так находят периметр разностороннего треугольника, ведь он имеет разные длины сторон. В данном случае 3, 4 и 5.
2) Так находят периметр равнобедренного треугольника, ведь две его стороны равны (умножением нашли их сумму) и прибавили 4 – длина третьей стороны.
3) Так находят периметр равностороннего треугольника, стороны которого равны.
Оформим задание в тетрадь.
Номер 7.
Рассмотри рисунок 2 на полях и запиши названия всех прямоугольных, остроугольных и тупоугольных треугольников; подчеркни названия равнобедренных треугольников.
Прямоугольные треугольники: KAD, KBO, ABO, KBC, DCO.
.jpg "Изображение математика 4 класс Моро, Бантова - 2 часть страница 96, номер 7, решение")
Повтори, какие бывают треугольники, а также виды углов.
Выпишем названия всех прямоугольных треугольников.
Прямоугольные треугольники: KAD, KBO, ABO, KBC, DCO.
Выпишем названия всех остроугольных треугольников.
Остроугольный треугольник: ADO.
Выпишем названия всех тупоугольных треугольников.
Тупоугольные треугольники: AOK, DCK, KOC.
Номер 8.
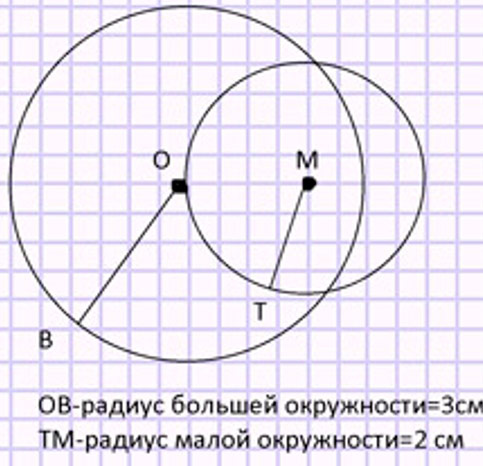
Начерти 2 окружности с радиусами 2 см и 3 см сначала с общим центром, а потом с разными центрами.
Ответ:
Повтори, что такое окружность и единицу длины – сантиметр.
Начертим окружности с общим центром.
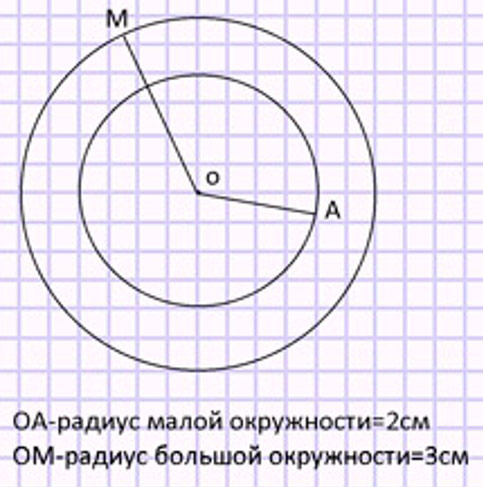
Начертим окружности с разными центрами.
Номер 9.
Найди длину ломаной АОКС (рис. 2).
Ответ:AOKC = АО + ОК + КС = 30 + 30 + 40 = 100 мм = 10 см
Повтори, что такое ломаная.
Найдем длину ломаной.
AOKC = АО + ОК + КС = 30 + 30 + 40 = 100 мм = 10 см
Оформим задание в тетрадь.
Правила о порядке выполнения действий
Номер 1.
(Устно.) Вычисли.
Ответ:
450 − 30 ∙ 4 + 70 : 10 = 450 − 120 + 7 = 330 + 7 = 337
280 : 7 + 160 ∙ 5 + 70 = 40 + 800 + 70 = 910
650 + 350 − 80 : 2 ∙ 5 = 1000 − 40 ∙ 5 = 1000 − 200 = 800
180 + 20 ∙ 6 − 75 : 25 = 180 + 120 − 3 = 297
Повтори случаи устного сложения и вычитания трёхзначных чисел, а также порядок действий.
Выполняем вычисления.
450 − 30 ∙ 4 + 70 : 10 = 337
В данном выражении необходимо сначала выполнить умножение и деление по порядку слева направо, а затем — сложение и вычитание также по порядку слева направо.
1) 30 ∙ 4 = 120
2) 70 : 10 = 7
3) 450 – 120 = 330
4) 330 + 7 = 337
280 : 7 + 160 ∙ 5 + 70 = 910
В данном выражении необходимо сначала выполнить умножение и деление по порядку слева направо, а затем — сложение и вычитание также по порядку слева направо.
1) 280 : 7 = 40
2) 160 ∙ 5 = 800
3) 40 + 800 = 840
4) 840 + 70 = 910
650 + 350 − 80 : 2 ∙ 5 = 800
В данном выражении необходимо сначала выполнить умножение и деление по порядку слева направо, а затем — сложение и вычитание также по порядку слева направо.
1) 80 : 2 = 40
2) 40 ∙ 5 = 200
3) 650 + 350 = 1000
4) 1000 – 200 = 800
180 + 20 ∙ 6 − 75 : 25 = 297
В данном выражении необходимо сначала выполнить умножение и деление по порядку слева направо, а затем — сложение и вычитание также по порядку слева направо.
1) 20 ∙ 6 = 120
2) 75 : 25 = 3
3) 180 + 120 = 300
4) 300 – 3 = 297
Оформляем задание в тетрадь.
450 − 30 ∙ 4 + 70 : 10 = 450 − 120 + 7 = 337
280 : 7 + 160 ∙ 5 + 70 = 40 + 800 + 70 = 910
650 + 350 − 80 : 2 ∙ 5 = 1000 − 40 ∙ 5 = 1000 − 200 = 800
180 + 20 ∙ 6 − 75 : 25 = 180 + 120 − 3 = 297
Номер 2.
Ответ:
Повтори, как умножать и делить круглые числа, а также порядок действий.
Выполняем вычисления.
980 – (150 + 30) : 30 = 974
В данном выражении сначала выполняется действие в скобках — сложение, затем — деление, а потом — вычитание.
1) 150 + 30 = 180
2) 180 : 30 = 6
3) 980 – 6 = 974
1600 + (470 – 70) ∙ 3 = 2800
В данном выражении сначала выполняется действие в скобках — вычитание, затем — умножение, а потом — сложение.
1) 470 – 70 = 400
2) 400 ∙ 3 = 1200
3) 1600 + 1200 = 400
400 ∙ 3 – (750 – 550) ∙ 4 = 400
В данном выражении сначала выполняется действие в скобках — вычитание, затем — умножение по порядку слева направо, а потом — вычитание.
1) 750 – 550 = 200
2) 400 ∙ 3 = 1200
3) 200 ∙ 4 = 800
4) 1200 – 800 = 400
820 + (1420 – 1400) ∙ 8 = 980
В данном выражении сначала выполняется действие в скобках — вычитание, затем — умножение, а потом — сложение.
1) 1420 – 1400 = 20
2) 20 ∙ 8 = 160
3) 820 + 160 = 980
Оформляем задание в тетрадь.
Номер 3.
Ответ:
Повтори случаи устного сложения и вычитания многозначных чисел, а также порядок действий.
Выполняем вычисления.
(860 + 40) – (560 – 60) : 100 = 895
В данном выражении сначала выполняются действия в скобках по порядку слева направо, затем — деление, а потом — вычитание.
1) 860 + 40 = 900
2) 560 – 60 = 500
3) 500 : 100 = 5
4) 900 – 5 = 895
(920 – 50) + (480 + 24) : 6 = 954
В данном выражении сначала выполняются действия в скобках по порядку слева направо, затем — деление, а потом — сложение.
1) 920 – 50 = 870
2) 480 + 24 = 504
3) 504 : 6 = 84
4) 870 + 84 = 954
2400 – (270 + 30) ∙ (400 – 396) = 1200
В данном выражении сначала выполняются действия в скобках по порядку слева направо, затем — умножение, а потом — вычитание.
1) 270 + 30 = 300
2) 400 – 396 = 4
3) 300 ∙ 4 = 1200
4) 2400 – 1200 = 1200
510 ∙ 6 – (780 – 20) + (230 + 470) = 3000
В данном выражении сначала выполняются действия в скобках по порядку слева направо, затем — умножение, потом — вычитание, и в конце — сложение.
1) 780 – 20 = 760
2) 230 + 470 = 700
3) 510 ∙ 6 = 3060
4) 3060 – 760 = 2300
5) 2300 + 700 = 3000
Оформляем задание в тетрадь.
Номер 4.
Поставь скобки, чтобы равенства были верными.
Ответ:
24 + 36 : (2 ∙ 3) = 30
(24 + 36) : 2 ∙ 3 = 90
(24 + 36 : 2) ∙ 3 = 126
(20 ∙ 9 − 6) : 3 = 58
20 ∙ (9 − 6 : 3) = 140
20 ∙ (9 − 6) : 3 = 20
Повтори случаи вне табличного умножения и деления, а также порядок действий.
Рассуждаем.
Чтобы равенства были верны, нужно расставить скобки.
24 + 36 : (2 ∙ 3) = 24 + 36 : 6 = 24 + 6 = 30
(24 + 36) : 2 ∙ 3 = 60 : 2 ∙ 3 = 30 ∙ 3 = 90
(24 + 36 : 2) ∙ 3 = (24 + 18) ∙ 3 = 42 ∙ 3 = 126
(20 ∙ 9 − 6) : 3 = (180 – 6) : 3 = 174 : 3 = 58
20 ∙ (9 − 6 : 3) = 20 ∙ (9 − 2) = 20 ∙ 7 = 140
20 ∙ (9 − 6) : 3 = 20 ∙ 3 : 3 = 60 : 3 = 20
Оформим задание в тетрадь.
24 + 36 : (2 ∙ 3) = 30
(24 + 36) : 2 ∙ 3 = 90
(24 + 36 : 2) ∙ 3 = 126
(20 ∙ 9 − 6) : 3 = 58
20 ∙ (9 − 6 : 3) = 140
20 ∙ (9 − 6) : 3 = 20
Номер 5.
Ответ:
Повтори, как называются числа при сложении, вычитании, умножении и делении.
Рассмотрим таблицы.
Выполняем вычисления.
Если b = 80 и a – b = 120, то
Чтобы найти уменьшаемое, нужно к разности прибавить вычитаемое.
а = 120 + 80 = 200
Чтобы найти сумму, нужно к первому слагаемому прибавить второе слагаемое.
a + b = 200 + 80 = 280
Если b = 90 и a + b = 290, то
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
а = 290 – 90 = 200
Чтобы найти разность, нужно из первого слагаемого вычесть второе слагаемое.
a – b = 200 – 90 = 110
Если а = 320 и a – b = 230, то
Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.
b = 320 – 230 = 90
Чтобы найти сумму, нужно к первому слагаемому прибавить второе слагаемое.
a + b = 320 + 90 = 410
Продолжаем вычисления.
Если с = 20 и c ∙ d = 80, то
Чтобы найти второй множитель, нужно произведение разделить на первый множитель.
d = 80 : 20 = 4
Чтобы найти частное, нужно делимое разделить на делитель.
c : d = 20 : 4 = 5
Если d = 5 и c : d = 8, то
Чтобы найти делимое, нужно частное умножить на делитель.
c = 8 ∙ 5 = 40
Чтобы найти произведение, нужно первый множитель умножить на второй множитель.
c ∙ d = 40 ∙ 5 = 200
Если с = 80 и c : d = 8, то
Чтобы найти делитель, нужно делимое разделить на частное.
d = 80 : 8 = 10
Чтобы найти произведение, нужно первый множитель умножить на второй множитель.
c ∙ d = 80 ∙ 10 = 800
Оформим задание в тетрадь.
Номер 6.
Найди значения выражений.
Ответ:
1) а + 320
а = 320
320 + 320 = 640
а = 400
400 + 320 = 720
а − 320
а = 320
320 − 320 = 0
а = 400
400 − 320 = 80
2) 720 ∙ b
b = 1
720 ∙ 1 = 720
b = 2
720 ∙ 2 = 1440
720 : b
b = 1
720 : 1 = 720
b = 2
720 : 2 = 360
Повтори, что такое буквенные выражения.
Рассуждаем.
Чтобы найти значение буквенного выражения, нужно в это выражение вместо буквы подставить данные числа и выполнить вычисления.
Если уменьшаемое и вычитаемое равны, то разность равна нулю.
Если один из двух множителей равен 1, то произведение равно другому множителю.
Если число разделить на 1, то получится число, которое делили.
Выполняем вычисления.
Если а = 320, то
а + 320 = 320 + 320 = 640
а – 320 = 320 – 320 = 0
Если а = 400, то
а + 320 = 400 + 320 = 720
а – 320 = 400 – 320 = 80
Продолжаем вычисления.
Если b = 1, то
720 ∙ b = 720 ∙ 1 = 720
720 : b = 720 : 1 = 720
Если b = 2, то
720 ∙ b = 720 ∙ 2 = 1440
720 : b = 720 : 2 = 360
Номер 7.
Вычисли.
Ответ:1)
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 96, номер 7, задание 1, 2024 год.")
2)
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 96, номер 7, задание 2, 2024 год.")
Повтори алгоритм письменного сложения, вычитания, умножения и деления многозначных чисел, а также порядок действий.
Выполняем вычисления.
8014 – 132 ∙ 54 + 44892 : 36 = 2133
В данном выражении сначала выполняется действие умножение, затем — деление, потом — вычитание, после чего — сложение.
1) 132 ∙ 54 = 7128
2) 44892 : 36 = 1247
3) 8014 – 7128 = 886
4) 886 + 1247 = 2133
7068 + 93840 : 46 – 506 ∙ 18 = 0
В данном выражении сначала выполняется действие деление, затем — умножение, потом — сложение, после чего — вычитание.
1) 93840 : 46 = 2040
2) 506 ∙ 18 = 9108
3) 7068 + 2040 = 9108
4) 9108 – 9108 = 0
1285 – 282 ∙ 75 : 47 + 14472 : 18 = 1639
В данном выражении сначала выполняется действие умножения, затем — деление по порядку слева направо, потом — вычитание, после чего — сложение.
1) 282 ∙ 75 = 21150
2) 21150 : 47 = 450
3) 14472 : 18 = 804
4) 1285 – 450 = 835
5) 835 + 804 = 1639
Продолжаем вычислять.
(47868 + 112812) : 52 + (27333 + 18615) : 84 = 3637
В данном выражении сначала выполняются действия в скобках по порядку слева направо, затем — деление по порядку слева направо, после чего — сложение.
1) 47868 + 112812 = 160680
2) 27333 + 18615 = 45948
3) 160680 : 52 = 3090
4) 45948 : 84 = 547
5) 3090 + 547 = 3637
(40600 – 38956) ∙ 33 – (15100 – 14125) ∙ 11 = 43527
В данном выражении сначала выполняются действия в скобках по порядку слева направо, затем — умножение по порядку слева направо, после чего — вычитание.
1) 40600 – 38956 = 1644
2) 15100 – 14125 = 975
3) 1644 ∙ 33 = 54252
4) 975 ∙ 11 = 10725
5) 54252 – 10725 = 43527
(576 + 126828 : 542) ∙ (406 ∙ 117 – 47000) = 406620
В данном выражении сначала выполняются действия в первой скобке: деление, потом — сложение, затем — действия во второй скобке: умножение, потом — вычитание, после чего — действие вне скобок — умножение.
1) 126828 : 542 = 234
2) 576 + 234 = 810
3) 406 ∙ 117 = 47502
4) 47502 – 47000 = 502
5) 810 ∙ 502 = 406620
(199430 – 119 ∙ 805) : (148 + 8536 : 88) = 423
1) 119 ∙ 805 = 95795
2) 199430 – 95795 = 103635
3) 8536 : 88 = 97
4) 148 + 97 = 245
5) 103635 : 245 = 423
Оформляем задание в тетрадь.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽
Напишите свой комментарий.