Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 94
- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
.jpg "Математика 4 класс Моро, Волкова - 2 часть страница 94")
Правила о порядке выполнения действий
Номер 1.
(Устно.) Вычисли.
Ответ:
450 − 30 ∙ 4 + 70 : 10 = 450 − 120 + 7 = 330 + 7 = 337
280 : 7 + 160 ∙ 5 + 70 = 40 + 800 + 70 = 910
650 + 350 − 80 : 2 ∙ 5 = 1000 − 40 ∙ 5 = 1000 − 200 = 800
180 + 20 ∙ 6 − 75 : 25 = 180 + 120 − 3 = 297
Повтори случаи устного сложения и вычитания трёхзначных чисел, а также порядок действий.
Выполняем вычисления первого столбика.
450 − 30 ∙ 4 + 70 : 10 = 450 − 120 + 7 = 330 + 7 = 337
280 : 7 + 160 ∙ 5 + 70 = 40 + 800 + 70 = 910
Выполняем вычисления второго столбика.
650 + 350 − 80 : 2 ∙ 5 = 1000 − 40 ∙ 5 = 1000 − 200 = 800
180 + 20 ∙ 6 − 75 : 25 = 180 + 120 − 3 = 297
Номер 2.
Ответ:
Повтори, как умножать и делить круглые числа, а также порядок действий.
Выполняем вычисления по действиям.
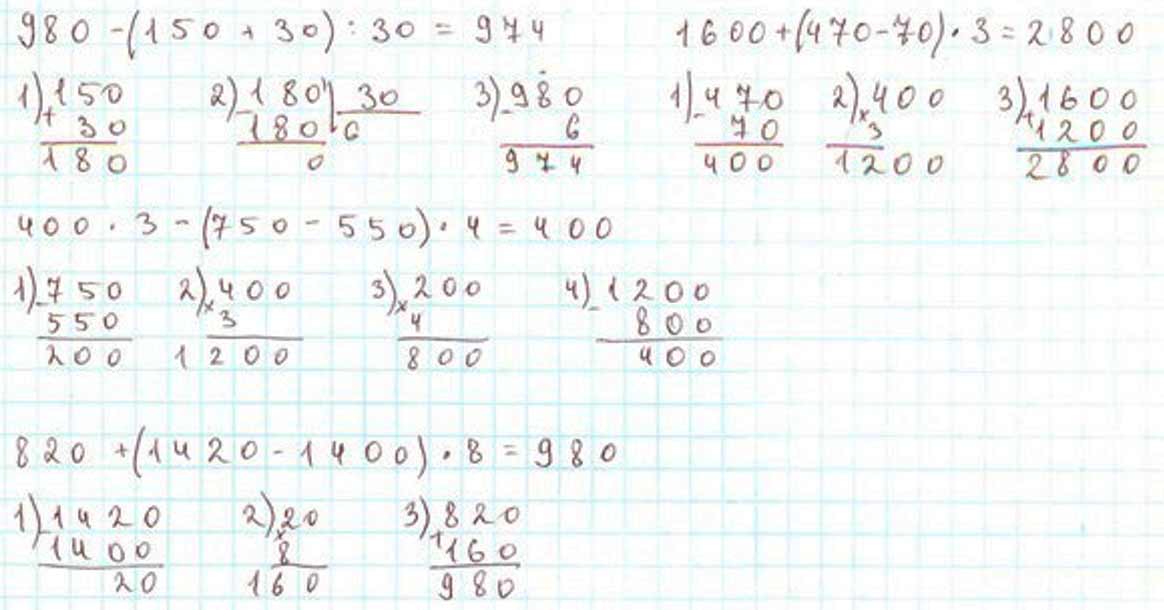
Оформляем задание в тетрадь.
980 – (150 + 30) : 30 = 974
1 600 + (470 – 70) ∙ 3 = 2 800
400 ∙ 3 – (750 – 550) ∙ 4 = 400
820 + (1 420 – 1 400) ∙ 8 = 980
Номер 3.
Ответ:
Повтори случаи устного сложения и вычитания многозначных чисел, а также порядок действий.
Выполняем вычисления по действиям.
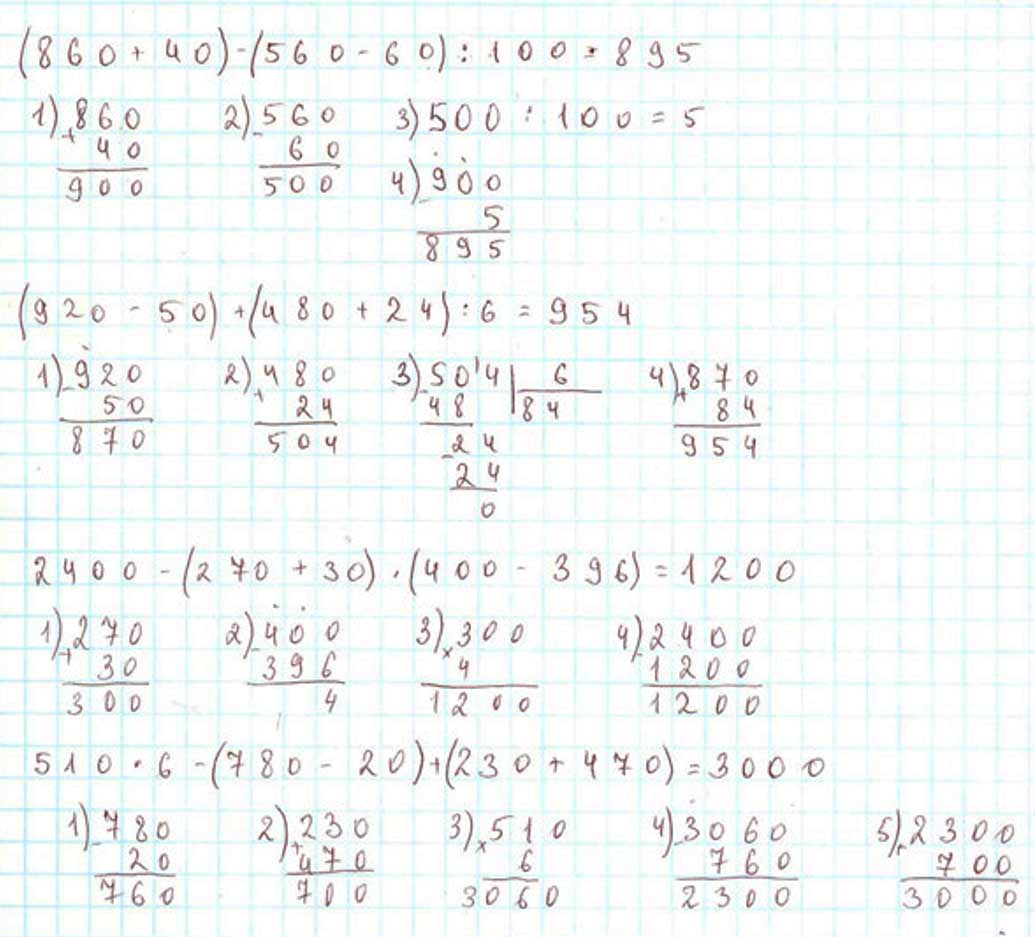
Оформляем задание в тетрадь.
(860 + 40) – (560 – 60) : 100 = 895
(920 – 50) + (480 + 24) : 6 = 786
2 400 – (270 + 30) ∙ (400 – 396) = 1 200
510 ∙ 6 – (780 – 20) + (230 + 470) = 3 000
Номер 4.
Поставь скобки, чтобы равенства были верными.
Ответ:
24 + 36 : (2 ∙ 3) = 24 + 36 : 6 = 24 + 6 = 30
(24 + 36) : 2 ∙ 3 = 60 : 2 * 3 = 30 * 3 = 90
(24 + 36 : 2) ∙ 3 = (24 + 18) * 3 = 42 * 3 = 126
(20 ∙ 9 − 6) : 3 = (180 - 6) : 3 = 174 : 3 = 58
20 ∙ (9 − 6 : 3) = 20 * (9 - 2) = 20 * 7 = 140
20 ∙ (9 − 6) : 3 = 20 * 3 : 3 = 60 : 3 = 20
Повтори случаи вне табличного умножения и деления, а также порядок действий.
Поставим скобки, чтобы равенства были верны.
24 + 36 : (2 ∙ 3) = 30
1) 2 ∙ 3 = 6
2) 36 : 6 = 6
3) 24 + 6 = 30
(24 + 36) : 2 ∙ 3 = 90
1) 24 + 36 = 60
2) 60 : 2 = 30
3) 30 ∙ 3 = 90
(24 + 36 : 2) ∙ 3 = 126
1) 36 : 2 = 18
2) 24 + 18 = 42
3) 42 ∙ 3 = 126
(20 ∙ 9 − 6) : 3 = 58
1) 20 ∙ 9 = 180
2) 180 – 6 = 174
3) 174 : 3 = 58
20 ∙ (9 − 6 : 3) = 140
1) 6 : 3 = 2
2) 9 – 2 = 7
3) 20 ∙ 7 = 140
20 ∙ (9 − 6) : 3 = 20
1) 9 – 6 = 3
2) 3 : 3 = 1
3) 20 ∙ 1 = 20
Оформим задание в тетрадь.
24 + 36 : (2 ∙ 3) = 30
(24 + 36) : 2 ∙ 3 = 90
(24 + 36 : 2) ∙ 3 = 126
(20 ∙ 9 − 6) : 3 = 58
20 ∙ (9 − 6 : 3) = 140
20 ∙ (9 − 6) : 3 = 20
Номер 5.
Ответ:
Повтори, как называются числа при сложении, вычитании, умножении и делении.
Выполняем вычисления с объяснением.
1)
Чтобы найти уменьшаемое, нужно к разности прибавить вычитаемое:
120 + 80 = 200.
Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность:
320 – 230 = 90.
Чтобы найти первое слагаемое, нужно из суммы вычесть второе слагаемое:
290 – 90 = 200.
Чтобы найти сумму, нужно к первому слагаемому прибавить второе слагаемое:
200 + 80 = 280;
320 + 90 = 410.
Чтобы найти разность, нужно из уменьшаемого вычесть вычитаемое:
200 – 90 = 110.
2)
Чтобы найти второй множитель, нужно произведение разделить на первый множитель:
80 : 20 = 4.
Чтобы найти делимое, нужно частное умножить на делитель:
8 ∙ 5 = 40.
Чтобы найти делитель, нужно делимое разделить на частное:
80 : 8 = 10.
Чтобы найти частное, нужно делимое разделить на делитель:
20 : 4 = 5.
Чтобы найти произведение, нужно первый множитель умножить на второй множитель:
40 ∙ 5 = 200;
80 ∙ 10 = 800.
Оформим задание в тетрадь.
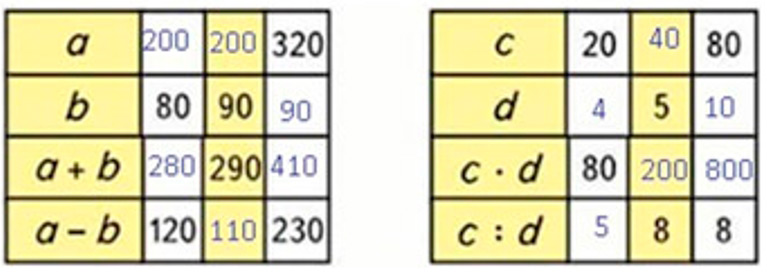
Номер 6.
Найди значения выражений.
Ответ:
1) а + 320
а = 320
320 + 320 = 640
а = 400
400 + 320 = 720
а − 320
а = 320
320 − 320 = 0
а = 400
400 − 320 = 80
2) 720 ∙ b
b = 1
720 ∙ 1 = 720
b = 2
720 ∙ 2 = 1440
720 : b
b = 1
720 : 1 = 720
b = 2
720 : 2 = 360
Повтори, что такое буквенные выражения.
Поясняем.
Чтобы найти значение буквенного выражения, нужно в это выражение вместо буквы подставить данные числа и выполнить вычисления.
Если уменьшаемое и вычитаемое равны, то разность равна нулю.
Если один из двух множителей равен 1, то произведение равно другому множителю.
Если число разделить на 1, то получится число, которое делили.
Выполняем вычисления и оформляем задание в тетрадь.
1) а + 320
а = 320
320 + 320 = 640
а = 400
400 + 320 = 720
а − 320
а = 320
320 − 320 = 0
а = 400
400 − 320 = 80
2) 720 ∙ b
b = 1
720 ∙ 1 = 720
b = 2
720 ∙ 2 = 1440
720 : b
b = 1
720 : 1 = 720
b = 2
720 : 2 = 360
Номер 7.
Вычисли.
Ответ:1)
.jpg "Изображение математика 4 класс Моро, Бантова - 2 часть страница 94, номер 7, задание 1")
2)
.jpg "Изображение математика 4 класс Моро, Бантова - 2 часть страница 94, номер 7, задание 2")
Повтори алгоритм письменного сложения, вычитания, умножения и деления многозначных чисел, а также порядок действий.
Выполняем вычисления.
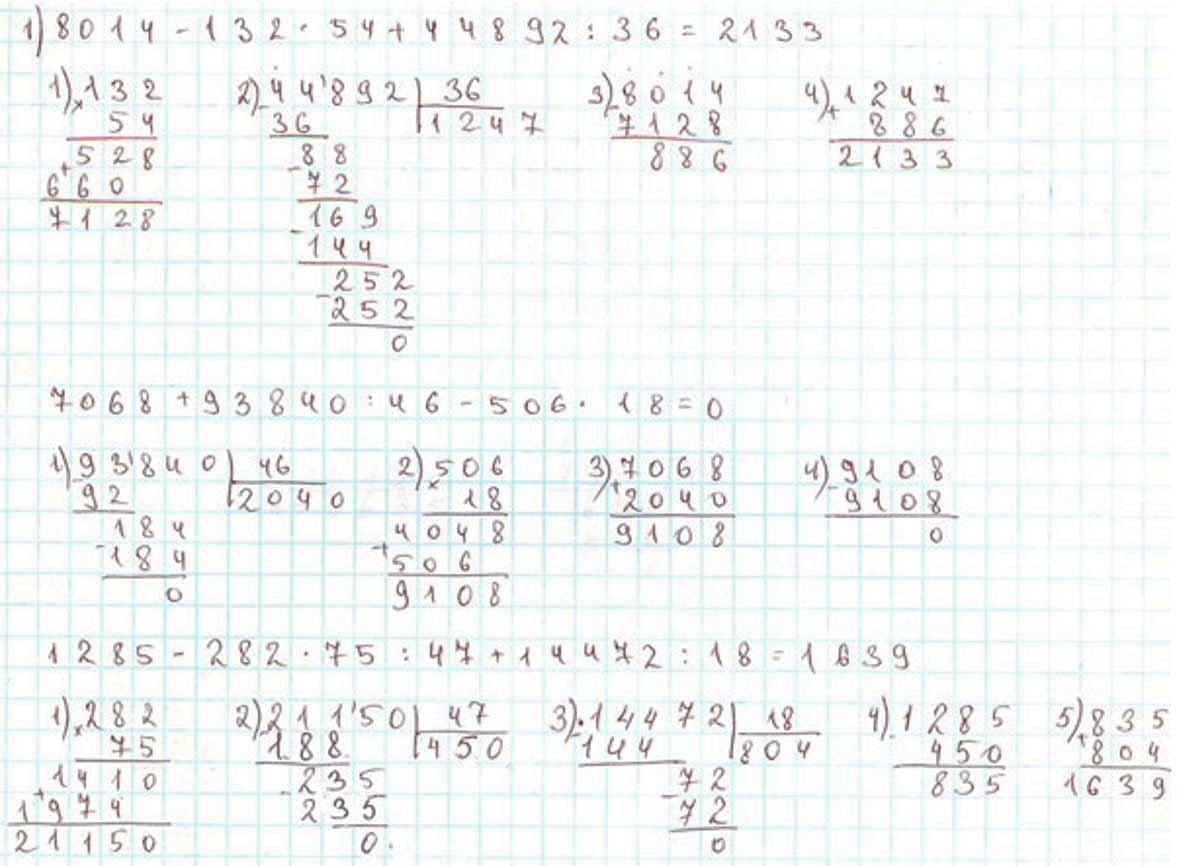
Продолжаем выполнять вычисления.
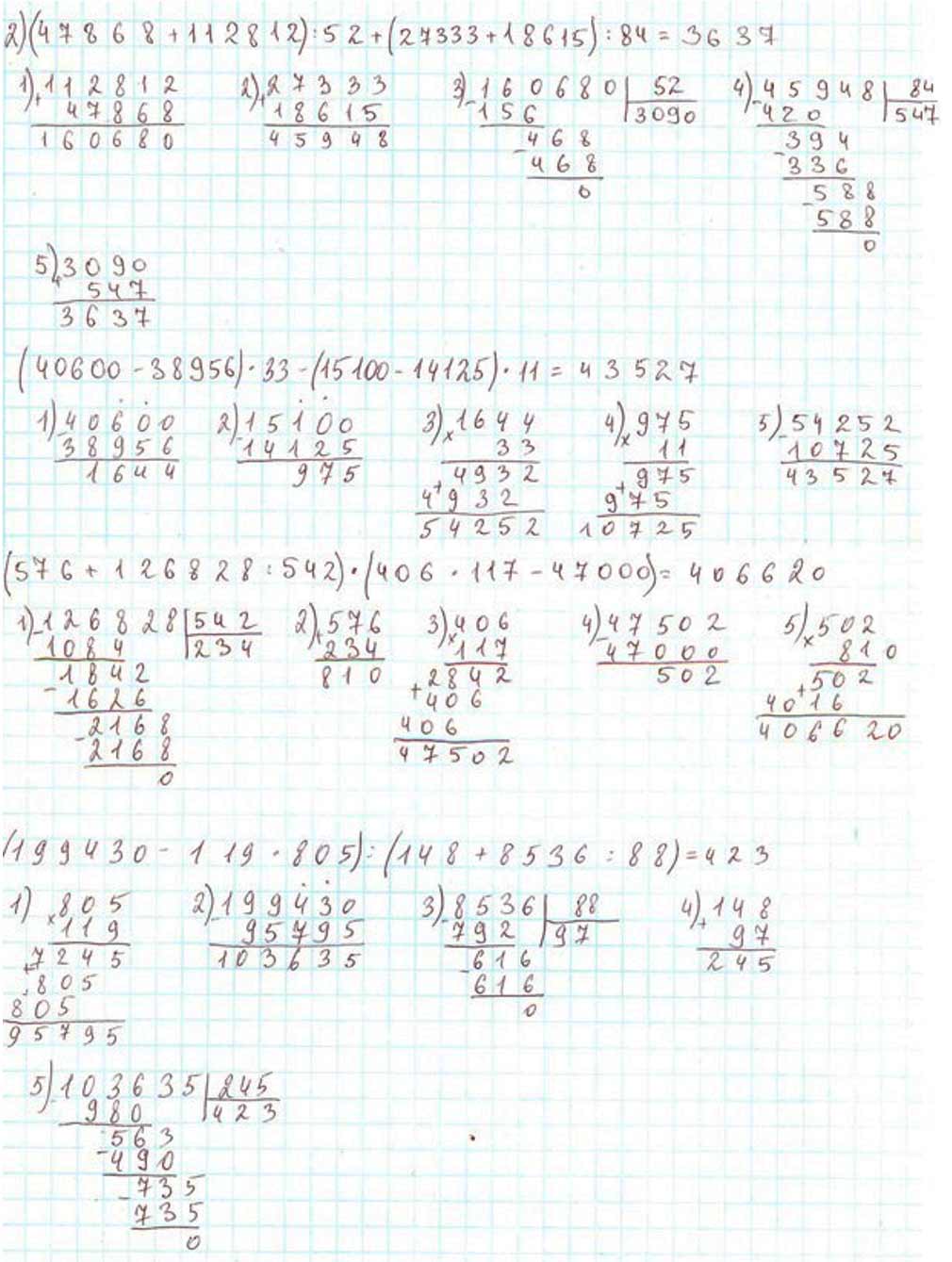
Оформляем задание в тетрадь.
Умножение и деление
Номер 1.
В каком случае сложение можно заменить умножением? Покажи на примерах.
Ответ:Умножение - более удобный способ нахождения суммы, состоящей из одинаковых слагаемых и повторяющихся несколько раз. Например: 5 + 5 + 5 = 5 ∙ 3 – можно заменить сложение умножением, а вот 4 + 4 + 4 + 2 – нельзя заменить, потому что сложение не состоит из одного вида слагаемого.
Номер 2.
Какими знаками обозначаются умножение и деление и как называются выражения, в которых числа соединены знаком умножения? знаком деления?
Ответ:Умножение обозначается знаком умножить “умножить” ( ∙ ). Деление обозначается знаком “разделить” ( : ). Выражения, в которых числа соединены знаком умножения, называются произведением. Выражения, в которых числа соединены знаком деления, называются частным.
Номер 3.
Покажи, как умножение можно заменить сложением.
Ответ:7 ∙ 3 = 7 + 7 + 7 38 ∙ 4 = 38 + 38 + 38 + 38 156 ∙ 2 = 156 + 156 9 ∙ 6 = 9 + 9 + 9 + 9 + 9 + 9
Номер 4.
Вставь знак >, < или = так, чтобы получилось верное равенство или неравенство.
Ответ:
37 ∙ 4 + 5 < 37 ∙ 5
Слева число 37 умножается на 4, значит это замена сложению 37 + 37 + 37 + 37.
Справа такое сложение выполняют 5 раз, то есть 37 + 37 + 37 + 37 + 37.
Слева прибавляется еще 5. Получается и слева и справа 5 слагаемых, но слева 5, а справа пятым является 37. 5 < 37, значит сумма слева меньше суммы справа.
68 ∙ 7 < 68 ∙ 7 + 68
Слева 68 ∙ 7 заменяет сумму, состоящую из 7 слагаемых каждое из которых равно 68, а справа сумма состоит из 8 слагаемых тоже равных 68.
Значение выражения слева меньше, чем значение выражения справа, так как справа большее число повторение слагаемых.
7 ∙ 9 = 7 ∙ 10 − 7
Слева 7 повторяют в сложении 9 раз и справа тоже, ведь выражение 7 ∙ 10 − 7 можно заменить выражением 7 ∙ 10 − 7 ∙ 1, а это равно 7 ∙ 9.
Номер 5.
Как называются при умножении и делении данные числа и число, которое получается в результате выполнения действия?
Ответ:
При умножении числа, которые умножаем называются первый множитель и второй множитель, а результат умножения − произведение.
Первый множитель ∙ второй множитель = произведение.
При делении число, которое делят, называется делимое, число, на которое делят − делитель, а результат − частное.
Делимое : делитель = частное.
Номер 6.
Прочитай, используя различные словесные формулировки, следующие равенства:
Ответ:
18 ∙ 3 = 54
1) Произведение 18 и 3 равно 54.
2) 18 умножить на 3 равно 54.
3) Если 18 умножить на 3, то получится 54.
4) Первый множитель 18, второй множитель 3, произведение 54.
128 : 4 = 32
1) 128 разделить на 4 равно 54.
2) Частное 128 и 4 равно 32.
3) Делимое 128, делитель 4, частное 32.
4) Если 128 разделить на 4, то получится 32.
Номер 7.
Составь и реши задачи на умножение и деление, используя слова: «Купили ... вещей по цене ... р.», «Сколько раз по ... содержится в ...?», «Сколько получится в каждой части, если ... разделить на ... равных частей?», «... больше в ... раз», «... меньше в ... раз», «Во сколько раз ... больше, чем ...?», «... в ... раз меньше, чем ...».
Ответ:
Задача 1:
Купили 5 альбомов по цене 25 р. Узнай стоимость покупки.
5 альбомов за ? р.
1 альбом – 25 р.
25 ∙ 5 = 125 (р.) – потратили на всю покупку.
Ответ: 125 рублей составляет общая стоимость покупки.
Задача 2:
В бочке 300 л воды, а в ведре 10 л. Сколько раз по 10 л содержится в 300 л?
В бочке – 300 л
В ведре – 10 л
? раз по 10 л в 300 л
300 : 10 = 30 (раз) – в 300 л содержится по 10 л.
Ответ: 30 раз в 300 л содержится по 10 л.
Задача 3:
Длина тесьмы 56 см. Сколько см получится в каждой части, если отрезок разделить на 7 одинаковых частей?
Длина всего – 56 см
Длина 1 части – ? см = 7 кусков
56 : 7 = 8 (см) – длина каждого куска, который получился при делении отрезка в 56 см на 7 кусков.
Ответ: длина каждого из семи кусков составляет 8 см.
Задача 4:
Велосипедист проехал 12 км. Ему осталось еще проехать в 2 раза больше. Сколько км велосипедист должен еще проехать?
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 94, номер 7, задача 4, 2024 год.")
12 ∙ 2 = 24 (км) – велосипедисту еще нужно проехать.
Ответ: 24 км всего нужно проехать велосипедисту.
Задача 5:
В корзине 18 кг яблок, а груш в 3 раза меньше. Сколько кг груш в корзине?
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 94, номер 7, задача 5, 2024 год.")
18 : 3 = 6 (кг) – груш лежат в корзине.
Ответ: 6 кг груш всего лежат в корзине.
Задача 6:
В автобусе 30 взрослых, а детей 10. Во сколько раз больше взрослых в автобусе, чем детей?
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 94, номер 7, задача 6, 2024 год.")
30 : 10 = 3 (раза) – во столько раз в автобусе больше взрослых, чем детей.
Ответ: в 3 раза больше человек в автобусе было взрослых, чем детей.
Задача 7:
Длина прямоугольного бассейна 8 м, а ширина 3 м. Длина стороны квадратной площадки 2 м. Во сколько раз площадь площадки меньше площади бассейна?
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 94, номер 7, задача 7, 2024 год.")
1) 8 ∙ 3 = 24 (м²) – площадь бассейна.
2) 2 ∙ 2 = 4 (м²) – площадь площадки.
3) 24 : 4 = 6 (раз) – во столько раз площадь площадки меньше, чем площадь бассейна.
Ответ: в 6 раз площадь площадки больше площади бассейна.
Номер 8.
Что получится, если 1) произведение двух чисел разделить на один из множителей; 2) умножить делитель на частное; 3) разделить делимое на частное?
Ответ:1) Получится другой множитель. 2) Получится делимое. 3) Получится делитель.
Номер 9.
1) Объясни два способа проверки умножения и деления.
2) Вычисли и сделай проверку.
1) Два способа проверки умножения и деления:
а) В первом случае для проверки произведение делят на второй множитель и получают первый, а во втором случае делят на первый множитель и получают второй.
б) В первом случае для проверки частное умножают на делитель и получают делимое, а во втором случае делимое делят на частное и получают делитель.
2)
Задание на полях страницы
Ребус.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽
Напишите свой комментарий.