Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 64
- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
.jpg "Математика 4 класс Моро, Волкова - 2 часть страница 64")
Номер 256.
Ответ:
Повтори алгоритм письменного деления и умножения на двузначные числа, вычитания многозначных чисел, а также порядок действий.
Выполняем вычисления по действиям.
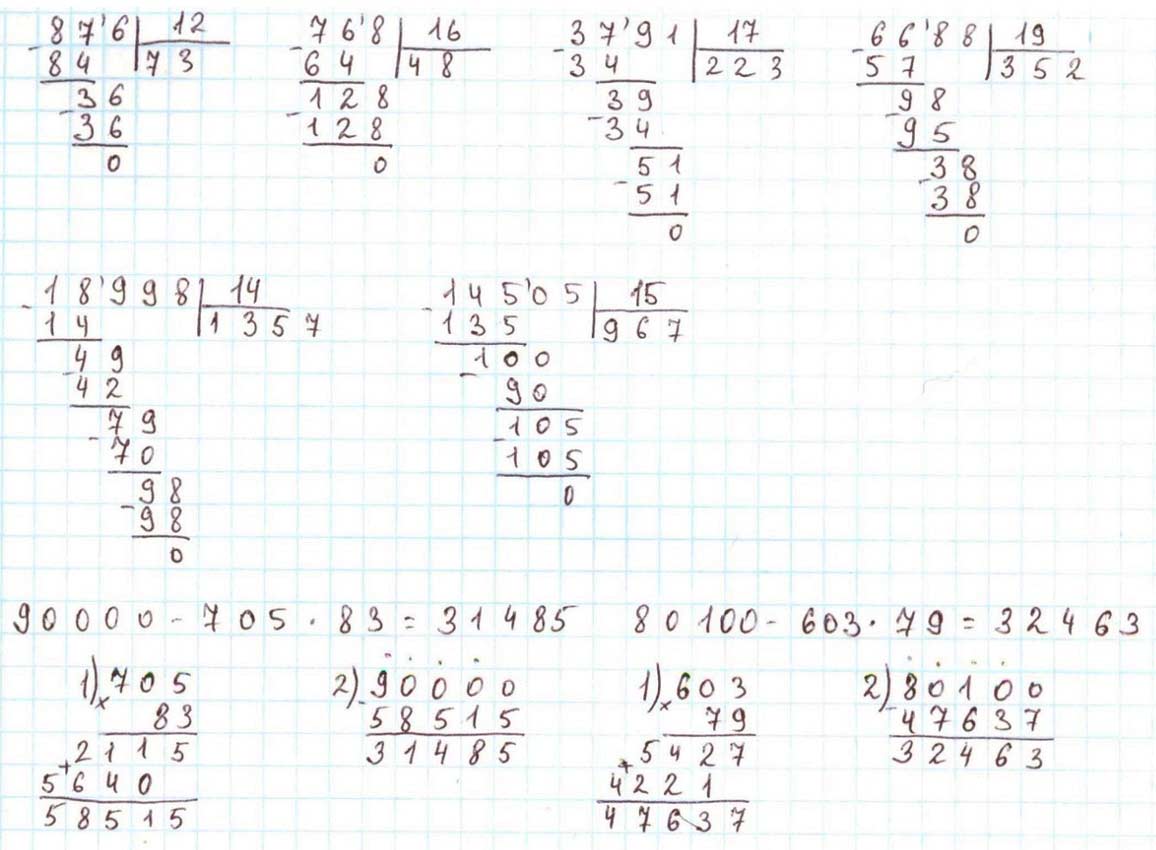
Оформляем задание в тетрадь.
90 000 – 705 ∙ 83 = 31 485
80 100 – 603 ∙ 79 = 32 463
Номер 257.
Реши задачи и сравни их решения.
1) Длина водохранилища 600 км, а его ширина 400 км. Поездка на катере через водохранилище по его длине занимает на 10 ч больше, чем по ширине. За сколько времени при одинаковой скорости можно пересечь водохранилище по его длине и по ширине?
2) Длина водохранилища на 200 км больше его ширины. Поездка на катере с одинаковой скоростью через водохранилище по его длине занимает 30 ч, а по ширине – 20 ч. Найди длину и ширину этого водохранилища.
Задача 1:
.jpg "Изображение математика 4 класс Моро, Бантова - 2 часть страница 64, номер 257 задача 1")
1) 600 − 400 = 200 (км) – расстояние, которое проходит катер за 10 ч.
2) 200 : 10 = 20 (км/ч) – скорость катера.
3) 600 : 20 = 30 (ч) – время поездки по длине водохранилища.
4) 400 : 20 = 20 (ч) – время поездки по ширине водохранилища.
Ответ: время поездки по длине водохранилища составляет 30 ч и время поездки по ширине водохранилища составляет 20 ч.
Задача 2:
.jpg "Изображение математика 4 класс Моро, Бантова - 2 часть страница 64, номер 257 задача 2")
1) 30 − 20 = 10 (ч) – время, за которое катер проходит расстояние в 200 км.
2) 200 : 10 = 20 (км/ч) – скорость катера.
3) 20 ∙ 30 = 600 (км) – длина водохранилища.
4) 20 ∙ 20 = 400 (км) – ширина водохранилища.
Ответ: длина водохранилища составляет 600 км и ширина водохранилища составляет 400 км.
Сравнение задач и их решений.
Эти задачи обратные. Рассмотрим решения задач. И в первой и во второй задаче сначала мы находили скорость катера, но в первой для этого мы искали неизвестное расстояние, которое проходят за 10 часов, а во второй - время, необходимое для прохождения расстояния в 200 км.
Затем искали нужное значение по вопросу задачи: в первой - время поездок по длине и ширине катера искали через деление: расстояние делили на найденную скорость, а во второй - длину и ширину водохранилища искали через умножение данных временных величин и найденной скорости.
Повтори взаимосвязь между скоростью, временем и расстоянием.
Шаг 1.
Оформляем условие в виде таблицы.
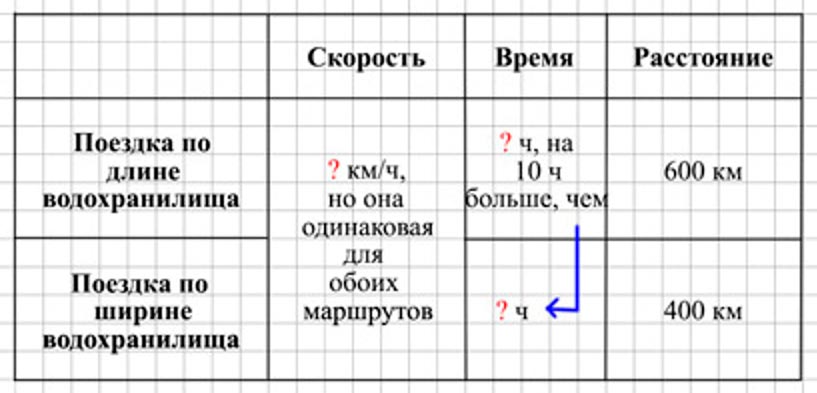
Рассуждаем.
Найдем расстояние, которое проходит катер за 10 часов.
1) 600 − 400 = 200 (км) – расстояние, которое проходит катер за 10 ч.
Продолжаем рассуждение.
Чтобы найти скорость катера, разделим расстояние на время.
2) 200 : 10 = 20 (км/ч) – скорость катера.
Продолжаем рассуждение.
Найдем, сколько времени катер будет ехать по длине водохранилища.
3) 600 : 20 = 30 (ч) – время поездки по длине водохранилища.
Продолжаем рассуждение.
Найдем, сколько времени катер будет ехать по ширине водохранилища.
4) 400 : 20 = 20 (ч) – время поездки по ширине водохранилища.
Записываем ответ.
Ответ: 30 ч и 20 ч.
Шаг 1.
Оформляем условие в виде таблицы.
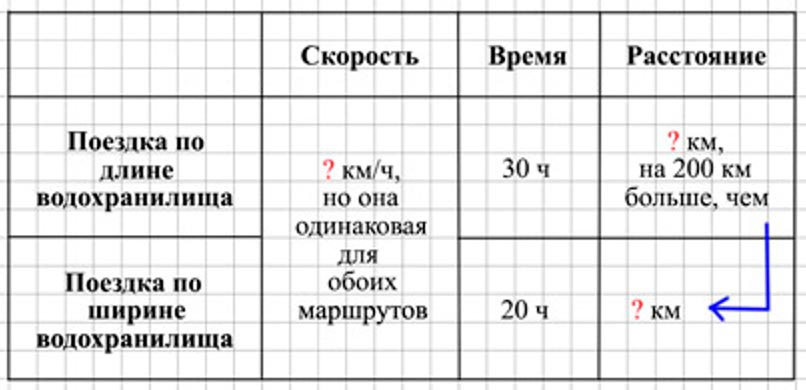
Рассуждаем.
Найдем время, за которое катер проходит расстояние в 200 км.
1) 30 − 20 = 10 (ч) – время, за которое катер проходит расстояние в 200 км.
Продолжаем рассуждение.
Чтобы найти скорость катера, разделим расстояние на время.
2) 200 : 10 = 20 (км/ч) – скорость катера.
Продолжаем рассуждение.
Найдем длину водохранилища, для этого скорость катера умножим на время в пути.
3) 20 ∙ 30 = 600 (км) – длина водохранилища.
Продолжаем рассуждение.
Найдем ширину водохранилища, для этого скорость катера умножим на время в пути.
4) 20 ∙ 20 = 400 (км) – ширина водохранилища.
Записываем ответ.
Ответ: 600 км и 400 км.
Сравниваем данные задачи и их решения.
Эти задачи обратные. Рассмотрим решения задач. И в первой и во второй задаче сначала мы находили скорость катера, но в первой для этого мы искали неизвестное расстояние, которое проходят за 10 часов, а во второй – время, необходимое для прохождения расстояния в 200 км.
Затем искали нужное значение по вопросу задачи: в первой – время поездок по длине и ширине катера искали через деление: расстояние делили на найденную скорость, а во второй – длину и ширину водохранилища искали через умножение данных временных величин и найденной скорости.
Номер 258.
В питомнике вырастили саженцы деревьев: елей было 360, а на каждый 8 елей приходилось 18 клёнов и 16 лип. Сколько всего елей, клёнов и лип вырастили в питомнике?
Ответ:
1) 360 : 8 = 45 (р.) – по 8 елей содержится в питомнике.
2) 18 ∙ 45 = 810 (шт.) – клёнов.
3) 45 ∙ 16 = 720 (шт.) – лип.
4) 360 + 810 + 720 = 1890 (шт.) – деревьев всего.
Ответ: 1890 елей, клёнов и лип вырастили в питомнике.
Повтори алгоритм сложения и деления трёхзначных чисел, умножения на двузначные числа, а также способы оформления краткой записи.
Оформляем условие в виде краткой записи.
Рассуждаем.
В питомнике было 360 елей, а на каждые 8 елей приходилось 18 кленов и 16 лип. Вычислим, сколько раз по 8 елей вырастили.
1) 360 : 8 = 45 (р.) – по 8 елей содержится в питомнике.
Продолжаем рассуждение.
Вырастили 45 раз по 18 кленов. Вычислим, сколько кленов вырастили.
2) 18 ∙ 45 = 810 (шт.) – клёнов.
Продолжаем рассуждение.
Вырастили 45 раз по 16 лип. Вычислим, сколько лип вырастили.
3) 45 ∙ 16 = 720 (шт.) – лип.
Продолжаем рассуждение.
Вырастили 360 елей, 810 кленов и 720 лип. Узнаем, сколько деревьев вырастили в питомнике.
4) 360 + 810 + 720 = 1890 (шт.) – деревьев, в питомнике.
Записываем ответ.
Ответ: 1890 деревьев.
Номер 259.
Ответ:
2 ц 50 кг ∙ 4 = 250 ц ∙ 4 = 1000 кг = 10 ц = 1 т
125 м ∙ 8 = 1000 м = 1 км
1 м 20 см ∙ 6 = 120 см ∙ 6 = 720 см = 7 м 20 см
1 м 20 см : 6 = 120 см : 6 = 20 см
2 мин 30 с ∙ 5 = 150 с ∙ 5 = 750 с = 12 мин 30 с
2 ч 30 мин : 5 = 150 мин : 5 = 30 мин
Повтори единицы массы – тонну, центнер и килограмм, единицы длины – километр, метр и сантиметр, а также единицы времени.
Выполняем вычисления с пояснениями.
1 ц = 100 кг, поэтому 2 ц 50 кг = 250 кг.
250 кг ∙ 4 = 1 000 кг = 1 т
125 м ∙ 8 = 1 000 м = 1 км
1 м = 100 см, поэтому 1 м 20 см = 120 см.
120 см ∙ 6 = 720 см = 7 м 20 см
120 см : 6 = 20 см
1 мин = 60 с, поэтому 2 мин 30 с = 150 с.
150 ∙ 5 = 750 с = 12 мин 30 с
1 ч = 60 мин, поэтому 2 ч 30 мин = 150 мин.
150 : 5 = 30 мин
Оформляем задание в тетрадь.
2 ц 50 кг ∙ 4 = 250 ц ∙ 4 = 1000 кг = 10 ц = 1 т
125 м ∙ 8 = 1000 м = 1 км
1 м 20 см ∙ 6 = 120 см ∙ 6 = 720 см = 7 м 20 см
1 м 20 см : 6 = 120 см : 6 = 20 см
2 мин 30 с ∙ 5 = 150 с ∙ 5 = 750 с = 12 мин 30 с
2 ч 30 мин : 5 = 150 мин : 5 = 30 мин
Номер 260.
Запиши неравенства и объясни, почему они верны.
1) Сумма чисел 289 и 1 больше их произведения.
2) Сумма чисел 289 и 0 больше их произведения.
3) Частное чисел 289 и 1 больше их разности.
1) 289 + 1 > 289 ∙ 1 − неравенство верно, так как когда мы прибавляем к числу 1, мы получаем число, большее на 1, а когда умножаем на 1, получаем число равное данному. 2) 289 + 0 > 289 ∙ 0 − неравенство верно, так как когда мы прибавляем к числу 0, мы получаем число, равное данному, а когда умножаем на 0, получаем 0. 3) 289 : 1 > 289 − 1 − неравенство верно, так как когда мы делим число на 1, то получаем число, равное данному, а когда вычитаем 1,получаем число, меньше данного на 1.
Повтори, как называются числа при сложении, вычитании, умножении и делении, а также что такое неравенства.
Выполняем вычисления с пояснениями.
1) 289 + 1 > 289 ∙ 1 − неравенство верно, так как когда мы прибавляем к числу 1, мы получаем число, большее на 1, а когда умножаем на 1, получаем число равное данному.
2) 289 + 0 > 289 ∙ 0 − неравенство верно, так как когда мы прибавляем к числу 0, мы получаем число, равное данному, а когда умножаем на 0, получаем 0.
3) 289 : 1 > 289 − 1 − неравенство верно, так как когда мы делим число на 1, то получаем число, равное данному, а когда вычитаем 1,получаем число, меньше данного на 1.
Оформляем задание в тетрадь.
289 + 1 > 289 ∙ 1
290 > 289
289 + 0 > 289 ∙ 0
289 > 0
289 : 1 > 289 – 1
289 > 288
Номер 261.
Реши те уравнения, в которых неизвестное находят умножением.
Ответ:
х : 100 = 90
х - неизвестное делимое.
Чтобы найти неизвестное делимое, нужно делитель умножить на частное.
Решается умножением.
Подходит.
х = 100 ∙ 90
х = 9000
1200 : х = 60
х - неизвестный делитель.
Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
Решается делением.
Не подходит.
30 ∙ х = 1800
х - неизвестный множитель.
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
Решается делением.
Не подходит.
х : 18 = 30
х - неизвестное делимое.
Чтобы найти неизвестное делимое, нужно делитель умножить на частное.
Решается умножением.
Подходит.
х = 30 ∙ 18
х = 540
Повтори, как решать уравнения.
Выполняем вычисления с объяснением.
х : 100 = 90
х – неизвестное делимое.
Чтобы найти неизвестное делимое, нужно делитель умножить на частное.
Решается умножением.
Подходит.
х = 100 ∙ 90
х = 9000
1200 : х = 60
х – неизвестный делитель.
Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
Решается делением.
Не подходит.
30 ∙ х = 1800
х – неизвестный множитель.
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
Решается делением.
Не подходит.
х : 18 = 30
х – неизвестное делимое.
Чтобы найти неизвестное делимое, нужно делитель умножить на частное.
Решается умножением.
Подходит.
х = 30 ∙ 18
х = 540
Оформляем задание в тетрадь.
Номер 262.
Докажи, что в каждой окружности все диаметры делятся центром окружности на 2 равных отрезка.
Ответ:
Диаметр – отрезок проходящий через центр окружности и ограниченный двумя точками окружности. Этим центром окружности диаметр делится на два равных радиуса. Все радиусы окружности равны, а значит все диаметры делятся центром окружности на 2 равных отрезка. Зелёные отрезки ОА, ОС, ОВ, OD равны по длине как радиусы одной окружности. Красные отрезки ОК, ОМ, ОР, ОL также равны как радиусы одной окружности.
Повтори, что такое окружность.
Рассмотрим данные окружности.
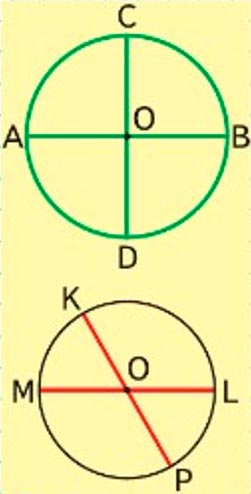
Доказываем.
Диаметр – отрезок, проходящий через центр окружности и ограниченный двумя точками окружности. Этим центром окружности диаметр делится на два равных радиуса. Все радиусы окружности равны, а значит, все диаметры делятся центром окружности на 2 равных отрезка.
Зелёные отрезки ОА, ОС, ОВ, OD равны по длине как радиусы одной окружности.
Красные отрезки ОК, ОМ, ОР, ОL также равны как радиусы одной окружности.
Номер 263.
Ответ:
Повтори алгоритм письменного вычитания, умножения и деления многозначных чисел, а также порядок действий.
Выполняем вычисления.
Оформляем задание в тетрадь.
17 256 – 256 ∙ 3 = 16 488
38 007 – 603 : 9 = 37 940
(205 167 – 123 068) ∙ 7 = 574 693
(31 280 + 14 320) ∙ 6 = 273 600
Номер 264.
Школьная хоккейная площадка длиной 50 м и шириной 20 м обнесена бортиком прямоугольной формы высотой 1 м. Сколько краски потребуется для окраски бортика с внешней и внутренней сторон, если расход краски на 1 м² составляет 140 г и краска должна быть нанесена в 2 слоя?
Ответ:
1) 50 ∙ 1 = 50 (м²) – площадь длинного бортика хоккейной площадки.
2) 20 ∙ 1 = 20 (м²) – площадь короткого бортика хоккейной площадки.
3) (50 + 20) ∙ 2 = 140 (м²) – площадь всех бортиков с одной стороны.
4) 140 ∙ 2 = 280 (м²) – площадь всех бортиков с двух сторон.
5) 280 ∙ 140 = 39200 (г) – расход краски, нужно для покраски бортиков в 1 слой.
6) 39200 ∙ 2 = 78400 (г) – краски нужно для покраски всех бортиков с двух сторон.
Ответ: 78400 грамм краски или 78 кг 400 грамм краски всего нужно для покраски всех бортиков с двух сторон.
Повтори единицу длины – метр, единицы массы – килограмм и грамм, а также единицы площади.
Оформляем условие в виде схематического чертежа.
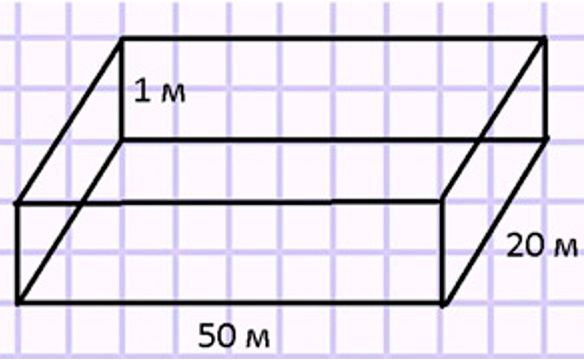
Рассуждаем.
Найдем площадь длинного бортика хоккейной площадки.
1) 50 ∙ 1 = 50 (м²) – площадь длинного бортика хоккейной площадки.
Продолжаем рассуждение.
Найдем площадь короткого бортика хоккейной площадки.
2) 20 ∙ 1 = 20 (м²) – площадь короткого бортика хоккейной площадки.
Продолжаем рассуждение.
Вычислим площадь всех бортиков с одной стороны площадки.
3) (50 + 20) ∙ 2 = 140 (м²) – площадь всех бортиков с одной стороны.
Продолжаем рассуждение.
Вычислим площадь всех бортиков с двух сторон.
4) 140 ∙ 2 = 280 (м²) – площадь всех бортиков с двух сторон.
Продолжаем рассуждение.
Вычислим расход краски, который нужен для покраски бортиков в 1 слой.
5) 280 ∙ 140 = 39200 (г) – расход краски, нужно для покраски бортиков в 1 слой.
Продолжаем рассуждение.
Вычислим расход краски, который нужен для покраски всех бортиков с двух сторон.
6) 39200 ∙ 2 = 78400 (г) – краски нужно для покраски всех бортиков с двух сторон.
Записываем ответ.
Ответ: 78400 грамм краски или 78 кг 400 грамм.
Задание внизу страницы
Вычисли.
Ответ:
Повтори единицы длины – метр и сантиметр.
Выполняем вычисления с пояснением.
1 м = 100 см, поэтому 5 м 30 см = 530 см
530 ∙ 6 = 3 180 см
3 180 см = 31 м 80 см
Оформляем задание в тетрадь.
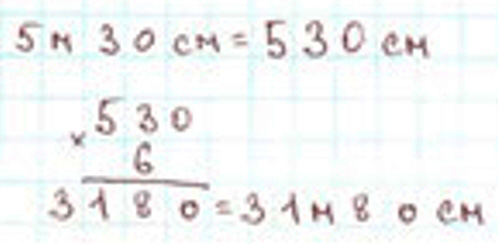
Задание на полях страницы
Ребус.
Ответ:
Перед нами ребус, для того чтобы найти недостающие цифры необходимо выполнить деление.
Рассмотрим ребус.
Разгадаем ребус.
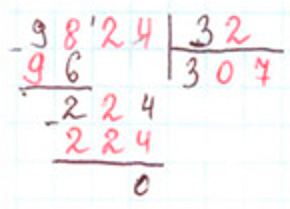
Первый неполный делитель – 98, так как при вычитании единиц вычли 6 и получился остаток 2, а 6 + 2 = 8.
На сколько надо умножить двузначное число с 3 десятками, чтобы получилось 96? Это число 3. Значит, первая цифра частного – 3, а делитель – 32, так как 32 ∙ 3 = 96.
Вторая цифра частного – 0, так как после того, как добавили к оставшимся сотням десятки, не получилось неполное делимое.
На какое число надо умножить 32, чтобы получилось трехзначное число с 2 сотнями и 4 единицами? Это число 7.
Пишу 7 в частное. 32 ∙ 7 = 224.
Оформим задание в тетрадь.
Номер 253.
Выполни деление с объяснением.
Ответ:
1) 5576 : 68 Для этого выделю первое неполное делимое – 557 (десятков). Нахожу первую цифру частного: 557 : 68 = 8 (десятков). Образую второе неполное делимое: 68 ∙ 8 = 544, 557 − 544 = 13 (десятков). Добавляю оставшиеся 6 единиц – 136. Нахожу вторую цифру частного: 136 : 68 = 2. Проверка:
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 64, номер 253, пример 1, 2024 год.")
Читаю ответ: при делении 5576 на 68 получается 82.
2) 1254 : 38
Для этого выделю первое неполное делимое – 125 (десятков).
Нахожу первую цифру частного: 125 : 38 = 3 (десятка).
Образую второе неполное делимое: 38 ∙ 3 = 114, 125 − 114 = 11 (десятков). Добавляю оставшиеся 4 единицы – 114.
Нахожу вторую цифру частного: 114 : 38 = 3.
Проверка:
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 64, номер 253, пример 2, 2024 год.")
Читаю ответ: при делении 1254 на 38 получится 33.
3) 23832 : 36
Для этого выделю первое неполное делимое – 238 (сотен).
Нахожу первую цифру частного: 238 : 36 = 6 (сотен).
Образую второе неполное делимое: 36 ∙ 6 = 216, 238 − 216 = 22 (сотни). Добавляю оставшиеся 3 десятка – 223.
Нахожу вторую цифру частного: 223 : 36 = 6 (десятков).
Образую третье неполное делимое: 36 ∙ 6 = 216, 223 − 216 = 7 (десятков). Добавлю оставшиеся 2 единицы – 72.
Нахожу третью цифру частного: 72 : 36 = 2.
Проверка:
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 64, номер 253, пример 3, 2024 год.")
Читаю ответ: при делении 23832 на 36 получится 662.
4) 11475 : 27
Для этого выделю первое неполное делимое – 114 (сотен).
Нахожу первую цифру частного: 114 : 27 = 4 (сотни).
Образую второе неполное делимое: 27 ∙ 4 = 108, 114 − 108 = 6 (сотен). Добавляю оставшиеся 7 десятков – 67.
Нахожу вторую цифру частного: 67 : 27 = 2 (десятка).
Образую третье неполное делимое: 27 ∙ 2 = 54, 67 − 54 = 13 (десятков). Добавлю оставшиеся 5 единиц – 135.
Нахожу третью цифру частного: 135 : 27 = 5.
Проверка:
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 64, номер 253, пример 4, 2024 год.")
Читаю ответ: при делении 11475 на 27 получится 425.
Номер 254.
Ответ:
Выражения 3 столбика, прежде чем решать, можно упростить.
Номер 255.
В торговом центре за день продали 52 одинаковых детских пальто и 8 костюмов по той же цене, что и пальто. За пальто получили на k р. больше, чем за костюмы. Запиши выражения, которые обозначают: 1) цену каждой вещи; 2) сколько денег получили за пальто и костюмы в отдельности.
Ответ:
1) k : (52 − 38) = k : 14 – цена одной вещи. 2) (k : 14) ∙ 52 – стоимость детских пальто. 3) (k : 14) ∙ 38 – стоимость костюмов.
Номер 256.
Масса угля в железнодорожном вагоне 60 т. Самосвал может взять третью часть этого груза. Сколько рейсов надо сделать на самосвале, чтобы разгрузить 6 таких вагонов?
Ответ:
1) 60 : 3 = 20 (т) – угля могут вместится в 1 самосвал.
2) 60 ∙ 6 = 360 (т) – масса угля в 6 вагонах.
3) 360 : 20 = 18 (р.) – нужно сделать самосвалу, чтобы разгрузить 6 вагонов.
Ответ: 18 рейсов всего нужно сделать самосвалу.
Номер 257.
В овощехранилище было 1280 ц моркови. Когда увезли морковь в магазины на 24 машинах, поровну на каждой, то в овощехранилище осталось 536 ц моркови. Сколько центнеров моркови увезли на каждой машине? Хватит ли 17 таких машин, чтобы вывезти оставшуюся морковь?
Ответ:
Было - 1280 ц моркови
Увезли - ? ц на 24 машинах одинаковой вместительности
Осталось - 536 ц на ? машинах той же вместительности
1) 1280 − 536 = 744 (ц) – моркови увезли.
2) 744 : 24 = 31 (ц) – моркови перевозит 1 машина.
3) 536 : 31 = 17 (ост.9)
536 : 31 = 17 (м) – 9 ц моркови останется в овощехранилище, значит, чтобы перевезти 536 ц моркови нужны 18 машин.
Ответ: 31 ц перевозит 1 машина; 17 машин не хватит, потому что останутся еще 9 центнеров моркови.
Номер 258.
Увеличь в 306 раз каждое из чисел: 780, 157, 407.
Ответ:
Номер 259.
Сумма трёх чисел равна 1480. Сумма первого и второго чисел равна 1230, сумма второго и третьего чисел - 1010. Найди каждое число.
Ответ:
1) 1480 − 1230 = 250 третье число.
2) 1010 − 250 = 760 второе число.
3) 1230 − 760 = 470 первое число.
Ответ: числа получились такими: первое число - 470, второе число - 760, третье число - 250.
Номер 260.
Спиши, заполняя пропуски.
Ответ:
4 м² = 400 дм²
8 м² = 80000 см²
63000 см² = 630 дм²
8100 дм² = 81 м²
5 сут. = 5 ∙ 24 = 120 ч
360 мин = 360 : 60 = 6 ч.
Номер 261.
Ответ:
Задание внизу страницы
Ответ:2 ч 30 мин = 150 мин 96 ч = 4 сут. 3 мин 26 с = 206 с
Задание на полях страницы
Ребус №1.
Ответ:
Ребус №2.
Ответ:
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 64, задание на полях страницы, ребус 2, 2024 год.")
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽
Напишите свой комментарий.