Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 55

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 12.
Сравни скорости, с которыми могут двигаться разные животные (с. 78–79).
Ответ:Переведем все представленные скорости в одной единице измерения (км/ч). Расстояние необходимо привести к единице км, а время – к часам.

Тогда табличка скоростей выглядит так:

Теперь сравним скорости животных.
А) По убыванию (начиная с самого быстрого):
1) стриж 120 км/ч;
2) гепард 108 км/ч;
3) антилопа 90 км/ч;
4) голубь 60 – 90 км/ч;
5) лев 80 км/ч;
6) зебра 60 км/ч;
7) воробей 30-60 км/ч;
8) жираф 45 км/ч;
9) аист 36 км/ч;
10) страус 30 км/ч.
Б) По возрастанию (начиная с самого медленного):
1) страус 30 км/ч;
2) аист 36 км/ч;
3) жираф 45 км/ч;
4) воробей 30 – 60 км/ч;
5) зебра 60 км/ч;
6) лев 80 км/ч;
7) голубь 60 – 90 км/ч;
8) антилопа 90 км/ч;
9) гепард 108 км/ч;
10) стриж 120 км/ч.
Повтори, в каких единицах измеряется скорость.
Переведем все представленные скорости к одной единице измерения.
Переведем все представленные скорости в одной единице измерения (км/ч).
Расстояние необходимо привести к единице км, а время – к часам.
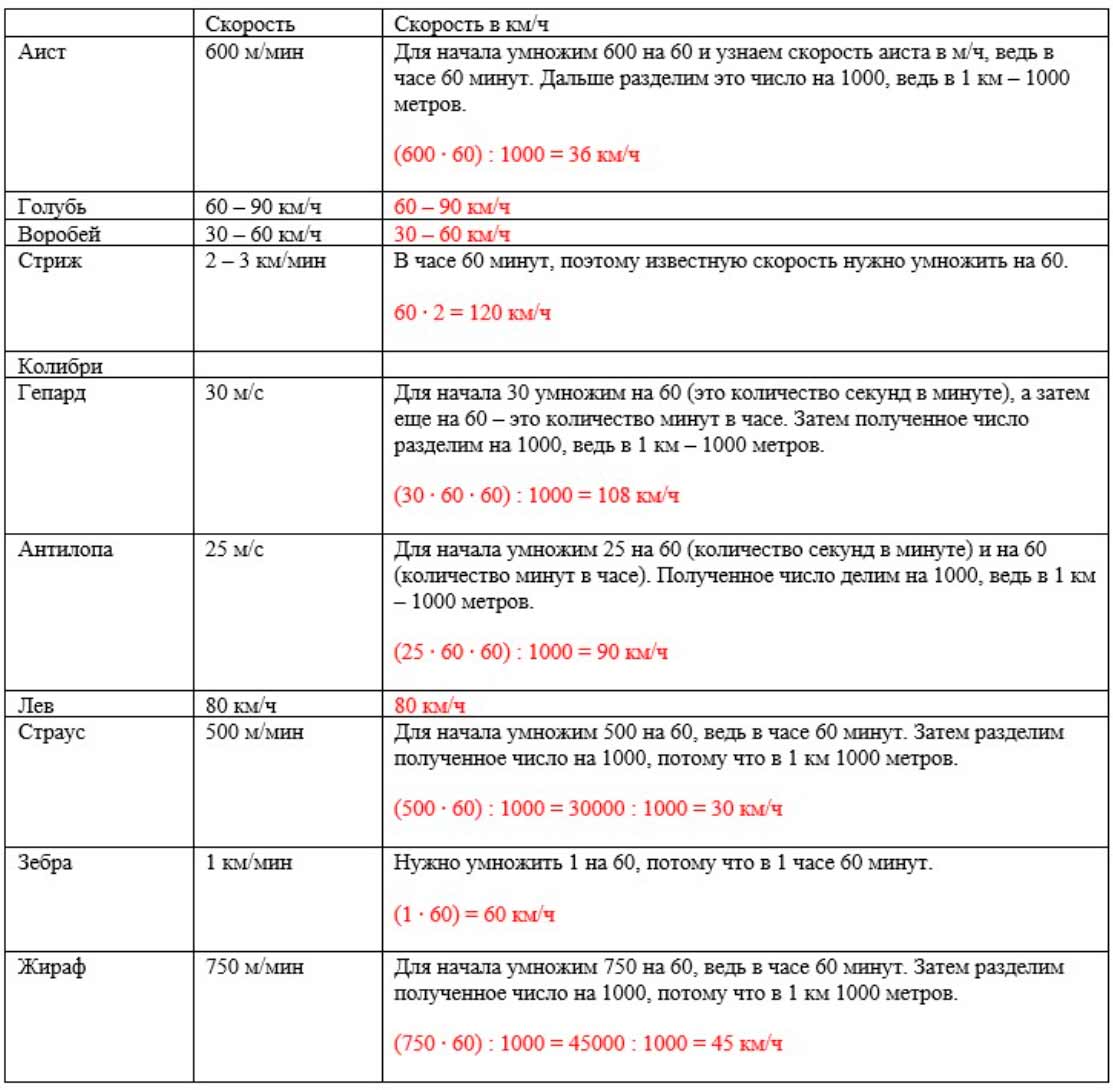
Тогда табличка скоростей выглядит так:
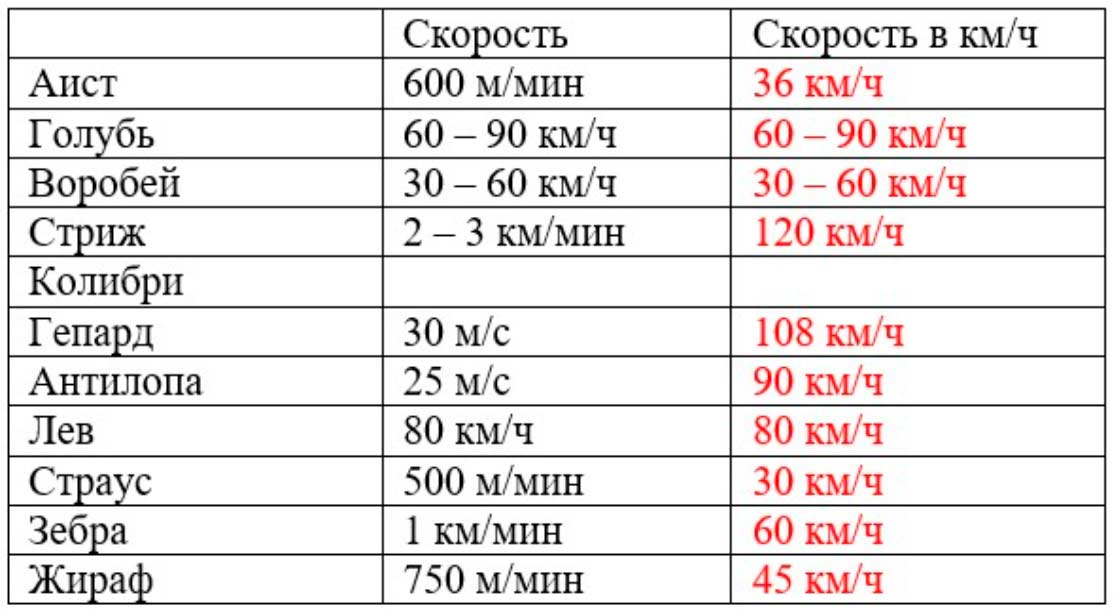
Сравним скорости животных.
А) По убыванию (начиная с самого быстрого):
1) стриж 120 км/ч;
2) гепард 108 км/ч;
3) антилопа 90 км/ч;
4) голубь 60 – 90 км/ч;
5) лев 80 км/ч;
6) зебра 60 км/ч;
7) воробей 30 – 60 км/ч;
8) жираф 45 км/ч;
9) аист 36 км/ч;
10) страус 30 км/ч.
Б) По возрастанию (начиная с самого медленного):
1) страус 30 км/ч;
2) аист 36 км/ч;
3) жираф 45 км/ч;
4) воробей 30 – 60 км/ч;
5) зебра 60 км/ч;
6) лев 80 км/ч;
7) голубь 60 – 90 км/ч;
8) антилопа 90 км/ч;
9) гепард 108 км/ч;
10) стриж 120 км/ч.
Оформим задание в тетрадь.
Номер 13.
1) Дана сумма 36 + 44. Каждое слагаемое увеличили в 20 раз. Проверь, увеличится ли в 20 раз значение суммы.
2) Дано произведение 15 ∙ 10. Первый множитель увеличили в 4 раза, а второй оставили без изменения. Проверь, увеличится ли в 4 раза значение произведения.
1) 36 + 44 = 80
20 ∙ 36 + 44 ∙ 20 = 720 + 880 = 1600
1600 : 80 = 20
Ответ: да, сумма увеличилась в 20 раз.
2) 15 ∙ 10 = 150
15 ∙ 4 ∙ 10 = 600
600 : 150 = 4
Ответ: да, произведение увеличилось в 4 раза.
Повтори, как называются числа при сложении и умножении.
Выполняем вычисления.
1) 36 + 44 = 80
20 ∙ 36 + 44 ∙ 20 = 720 + 880 = 1600
1600 : 80 = 20
Ответ: да, сумма увеличилась в 20 раз.
2) 15 ∙ 10 = 150
15 ∙ 4 ∙ 10 = 600
600 : 150 = 4
Ответ: да, произведение увеличилось в 4 раза.
Оформляем задание в тетрадь.
Номер 14.
Ответ:
Повтори алгоритм умножения на двузначные и трёхзначные числа, деления на двузначные, а также порядок действий.
Выполняем вычисления по действиям.
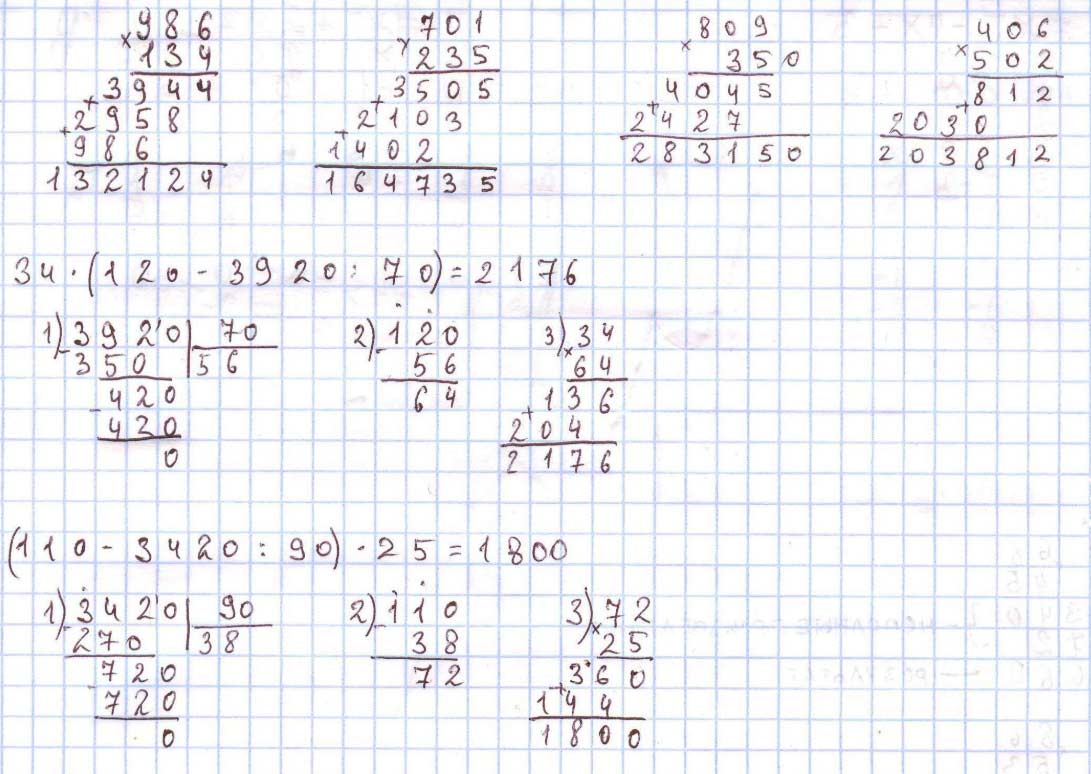
Оформляем задание в тетрадь.
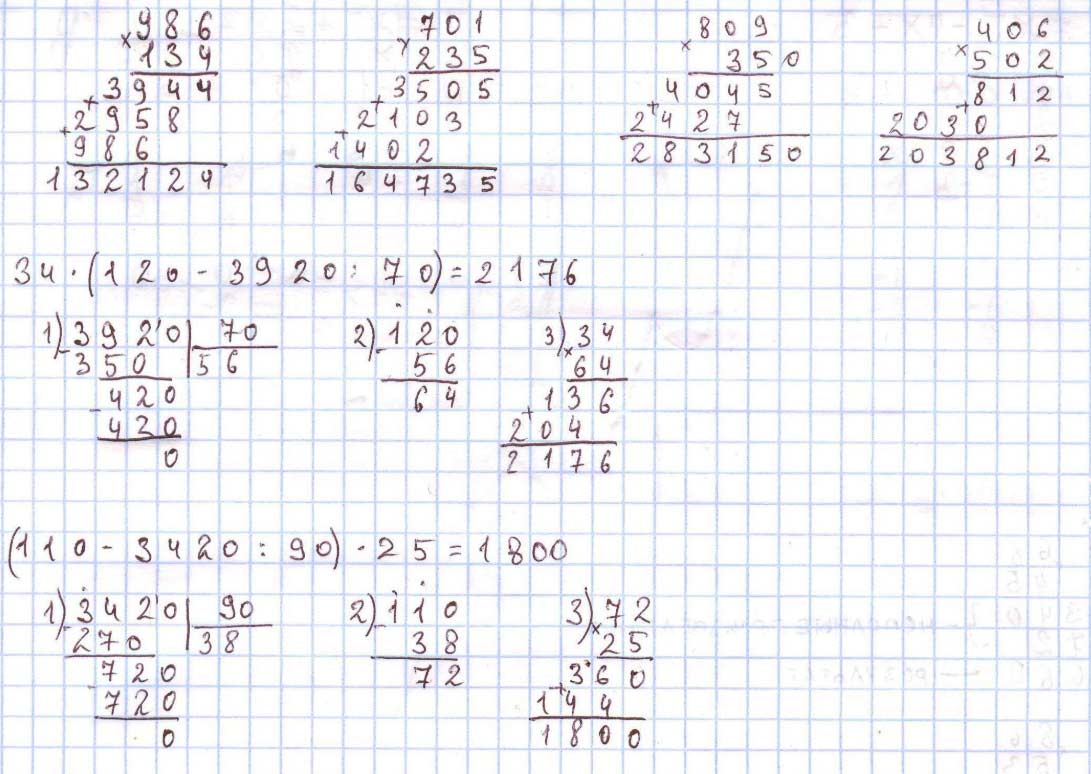
34 ∙ (120 – 3 920 : 70) = 2 176
(110 – 3 420 : 90) ∙ 25 = 1 800
Номер 15.
Выполни деление с остатком.
Ответ:
Повтори алгоритм деления с остатком.
Выполняем вычисление первого примера с пояснением.
Первое неполное делимое – 44 десятка. В записи частного будет 2 цифры.
Разделю 44 на 10. Для этого разделю 4 на 1, получу 4 – столько десятков будет в частном.
Умножу 10 на 4, получу 40 – столько десятков разделили.
Вычту 40 из 44, получу 4 – столько десятков осталось разделить.
Сравню остаток с делителем: десятков осталось меньше, чем 10.
Второе неполное делимое – 48 единиц.
Разделю 48 на 10. Для этого разделю 4 на 1, получу 4 – столько единиц будет в частном.
Умножу 10 на 4, получу 40 – столько единиц разделили.
Вычту 40 из 48, получу 8 – столько единиц осталось разделить.
Сравню остаток с делителем: единиц осталось меньше, чем 40.
Читаю ответ: частное равно 44, остаток 8.
Далее рассуждаю аналогично.
Выполняем вычисления и оформляем задание в тетрадь.
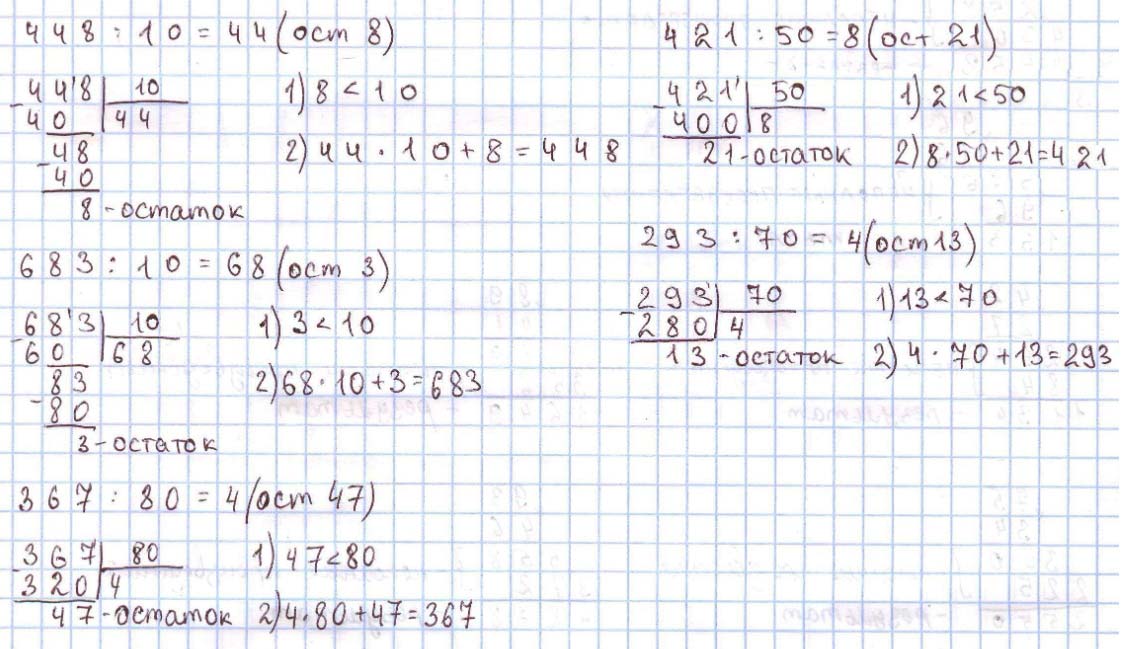
Номер 16.
Составь и реши задачи по рисункам животных (с. 79).
Ответ:Задача 1: Голубь и стриж одновременно вылетели из дома сороки и после сытного ужина решила немного пролететься. Голубь полетел налево, а воробей направо, причем в пути птицы были 2 часа. На каком расстоянии оказалась каждая птица от домика сороки, если известно, что скорость воробья 50 км/ч, а голубя на 30 км/ч больше?

1) 50 + 30 = 80 (км/ч) – скорость с которой летел голубь.
2) 80 ∙ 2 = 160 (км) – пролетел голубь.
3) 50 ∙ 2 = 100 (км) – пролетел воробей.
Ответ: 160 км пролетел голубь и 100 км пролетел воробей.
Задача 2:
Зебра и Жираф – два старых друга решили пойти к другу гепарду и заодно узнать, кто же придет быстрее. На сколько часов раньше придет в гости к гепарду зебра, если ее скорость 60 км/ч, а скорость жирафа – 45 км/ч. До домика Гепарда животным нужно бежать 180 км.
.jpg)
1) 180 : 60 = 3 (ч) – будет бежать зебра до домика гепарда.
2) 180 : 45 = 4 (ч) – будет бежать жираф до домика гепарда.
3) 4 − 3 = 1 (ч) – на столько часов раньше зебра доберется до дома гепарда.
Ответ: на 1 час раньше зебра доберётся до дома гепарда.
Задача 3:
Лев и страус бежали к водопою. Страусу до водопоя нужно было пройти 60 км, а льву 160. Кто первым придет к водопою, если скорость льва – 80 км/ч, а скорость страуса на 50 км/ч меньше?
.jpg)
1) 80 − 50 = 30 (км/ч) – скорость страуса.
2) 60 : 30 = 2 (ч) – потребуются страусу, чтобы добраться до водопоя.
3) 160 : 80 = 2 (ч) – потребуются льву, чтобы добежать до водопоя.
И льву и страусу потребуются 2 часа, чтобы добраться до водопоя, а это значит, что они придут туда в одно и тоже время.
Ответ: они доберутся до водопоя одновременно.
Повтори взаимосвязь между скоростью, временем и расстоянием.
Шаг 1.
Составляем первую задачу.
Голубь и стриж одновременно вылетели из дома сороки и после сытного ужина решили немного пролететь. Голубь полетел налево, а воробей направо, причем в пути птицы были 2 часа. На каком расстоянии оказалась каждая птица от домика сороки, если известно, что скорость воробья 50 км/ч, а голубя на 30 км/ч больше?
Оформляем условие в виде схематического чертежа.
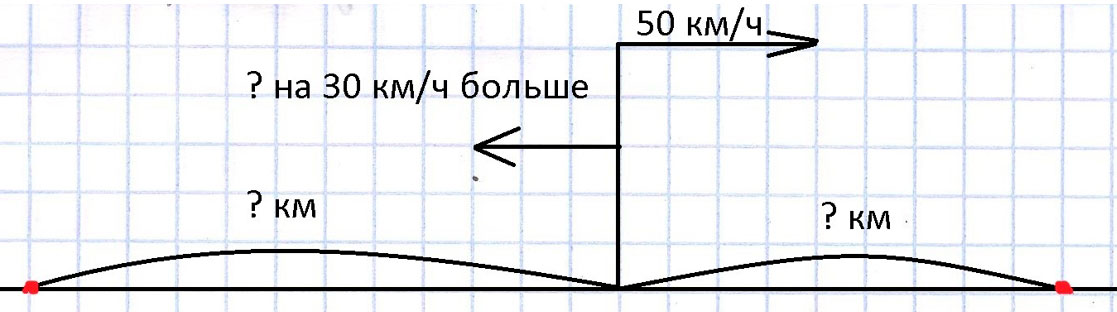
Рассуждаем.
Узнаем скорость, с которой летел голубь.
1) 50 + 30 = 80 (км/ч) – скорость, с которой летел голубь.
Продолжаем рассуждение.
Теперь мы можем узнать, какое расстояние пролетел голубь, для этого скорость умножим на время.
2) 80 ∙ 2 = 160 (км) – пролетел голубь.
Продолжаем рассуждение.
Теперь мы можем узнать, какое расстояние пролетел воробей, для этого скорость умножим на время.
3) 50 ∙ 2 = 100 (км) – пролетел воробей.
Записываем ответ.
Ответ: 160 км и 100 км.
Шаг 1.
Составляем вторую задачу.
Зебра и Жираф – два старых друга решили пойти к другу гепарду и заодно узнать, кто же придет быстрее. На сколько часов раньше придет в гости к гепарду зебра, если ее скорость 60 км/ч, а скорость жирафа – 45 км/ч. До домика Гепарда животным нужно бежать 180 км.
Оформляем условие в виде схематического чертежа.

Рассуждаем.
Узнаем, какое время будет бежать зебра до домика гепарда.
1) 180 : 60 = 3 (ч) – будет бежать зебра до домика гепарда.
Продолжаем рассуждение.
Узнаем, какое время будет бежать жираф до домика гепарда.
2) 180 : 45 = 4 (ч) – будет бежать жираф до домика гепарда.
Продолжаем рассуждение.
Узнаем, на сколько раньше зебра доберется до дома гепарда, чем жираф.
3) 4 − 3 = 1 (ч) – на столько часов раньше зебра доберется до дома гепарда.
Записываем ответ.
Ответ: на 1 час раньше.
Шаг 1.
Составляем третью задачу.
Лев и страус бежали к водопою. Страусу до водопоя нужно было пройти 60 км, а льву 160. Кто первым придет к водопою, если скорость льва – 80 км/ч, а скорость страуса на 50 км/ч меньше?
Оформляем условие в виде схематического чертежа.
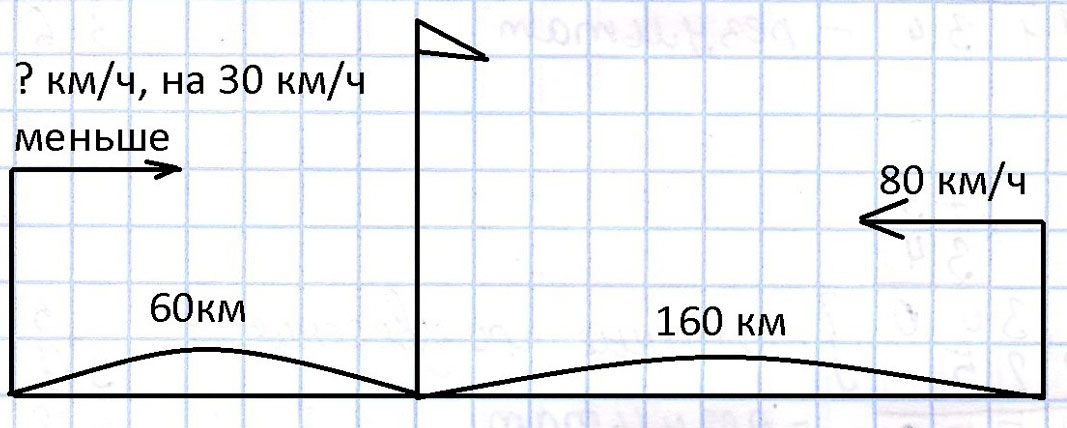
Рассуждаем.
Узнаем, какова скорость страуса.
1) 80 − 50 = 30 (км/ч) – скорость страуса.
Продолжаем рассуждение.
Узнаем, сколько времени потребуется страусу, чтобы добраться до водопоя.
2) 60 : 30 = 2 (ч) – потребуются страусу, чтобы добраться до водопоя.
Продолжаем рассуждение.
Узнаем, сколько времени потребуется льву, чтобы добраться до водопоя.
3) 160 : 80 = 2 (ч) – потребуются льву, чтобы добежать до водопоя.
И льву и страусу потребуются 2 часа, чтобы добраться до водопоя, а это значит, что они придут туда в одно и тоже время.
Записываем ответ.
Ответ: они доберутся до водопоя одновременно.
Номер 17.
Реши задачи и сравни их решения.
1) В один магазин привезли 18 одинаковых бидонов молока, а в другой – 12 таких же бидонов. В первый магазин привезли на 228 л молока больше, чем во второй. Сколько литров молока привезли в каждый магазин?
2) В один магазин привезли в одинаковых бидонах 684 л молока, а в другой – 456 л молока в таких же бидонах. В первый магазин привезли на 6 бидонов молока больше, чем во второй. Сколько бидонов молока привезли в каждый магазин?
Задача 1:

1) 18 − 12 = 6 (б.) – на столько больше бидонов привезли в первый магазин, чем во второй магазин. 2) 228 : 6 = 38 (л) – столько литров молока содержится в одном бидоне.

3) 38 ∙ 18 = 684 (л) – молока привезли в первый магазин.

4) 38 ∙ 12 = 456 (л) – молока привезли во второй магазин.

Ответ: 684 л молока привезли в первый магазин и 456 литров молока привезли во второй магазин.
Задача 2:

1) 684 − 456 = 228 (л) – на столько больше молока привезли в первый магазин, чем во второй.

2) 228 : 6 = 38 (л) – молока содержится в 1 бидоне.

3) 684 : 38 = 18 (б.) – молока привезли в первый магазин.

4) 456 : 38 = 12 (б.) – молока привезли во второй магазин.

Ответ: 18 бидонов молока всего привезли в первый магазин и 12 бидонов молока всего привезли во второй магазин.
Сравнение задач и их решений:
В первой задаче нам известно количество бидонов и то, на сколько литров больше привезли в первый магазин, чем во второй, а во второй задаче наоборот: нам известно количество литров молока, привезенных в магазины и сказано, что в первый магазин привезли на 6 бидонов больше.
Первым действием мы находим разницу количества молока, привезенного в два магазина-это в первой задаче, а во второй-между бидонами. Затем делим количество литров на количество бидонов и узнаем емкость одного бидона.
Также есть еще одно различие: в первой задаче мы умножаем полученное значение на количество бидонов, привезенных в каждый магазин, и находим количество молока(в литрах), а во второй наоборот делим известные величины(количество привезенного молока в литрах) на емкость одного бидона и находим количество бидонов, привезенных в каждый магазин.
Эти задачи можно считать обратными.
Повтори единицу объёма – литр.
Шаг 1.
Оформляем условие в виде схематического чертежа.

Рассуждаем.
Узнаем, насколько больше бидонов привезли во второй магазин.
1) 18 − 12 = 6 (б.) – настолько больше бидонов привезли во второй магазин, чем в первый магазин.
Продолжаем рассуждение.
Узнаем, сколько литров молока содержится в одном бидоне.
2) 228 : 6 = 38 (л) – столько литров молока содержится в одном бидоне.
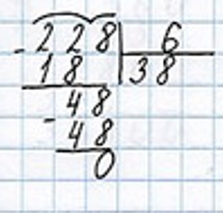
Продолжаем рассуждение.
Узнаем, сколько молока привезли в первый магазин.
3) 38 ∙ 18 = 684 (л) – молока привезли в первый магазин.

Продолжаем рассуждение.
Узнаем, сколько молока привезли во второй магазин.
4) 12 ∙ 38 = 456 (л) – молока привезли во второй магазин.
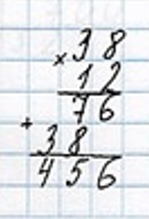
Записываем ответ.
Ответ: 684 и 456 литров.
Шаг 1.
Оформляем условие в виде схематического чертежа.

Рассуждаем.
Узнаем, насколько больше молока привезли в первый магазин, чем во второй.
1) 684 − 456 = 228 (л) – настолько больше молока привезли в первый магазин, чем во второй.
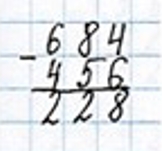
Продолжаем рассуждение.
Узнаем, сколько молока содержится в одном бидоне.
2) 228 : 6 = 38 (л) – молока содержится в 1 бидоне.
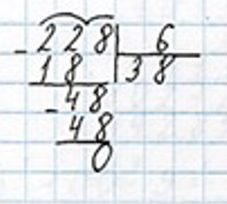
Продолжаем рассуждение.
Узнаем, сколько молока привезли в первый магазин.
3) 684 : 38 = 18 (б.) – молока привезли в первый магазин.
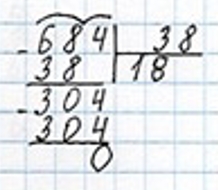
Продолжаем рассуждение.
Узнаем, сколько молока привезли во второй магазин.
4) 456 : 38 = 12 (б.) – молока привезли во второй магазин
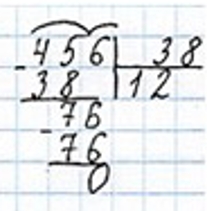
Записываем ответ.
Ответ: 18 и 12 бидонов.
Сравнение задач и их решений.
В первой задаче нам известно количество бидонов и то, на сколько литров больше привезли в первый магазин, чем во второй, а во второй задаче наоборот: нам известно количество литров молока, привезенных в магазины и сказано, что в первый магазин привезли на 6 бидонов больше.
Первым действием мы находим разницу количества молока, привезенного в два магазина – это в первой задаче, а во второй – между бидонами. Затем делим количество литров на количество бидонов и узнаем емкость одного бидона.
Также есть еще одно различие: в первой задаче мы умножаем полученное значение на количество бидонов, привезенных в каждый магазин, и находим количество молока (в литрах), а во второй наоборот делим известные величины (количество привезенного молока в литрах) на емкость одного бидона и находим количество бидонов, привезенных в каждый магазин.
Эти задачи можно считать обратными.
Номер 18.
Реши уравнения.
Ответ:
х − 12 = 0
х = 12 + 0
х = 12
Проверка:
12 - 12 = 0
0 = 0
Ответ: х = 12
25 + х = 25
х = 25 − 25
х = 0
Проверка:
25 + 0 = 25
25 = 25
Ответ: х = 0
х : 108 = 1
х = 108 ∙ 1
х = 108
Проверка:
108 : 108 = 1
1 = 1
Ответ: х = 108
у : 1 = 37
у = 37 ∙ 1
у = 37
Проверка:
37 : 1 = 37
37 = 37
Ответ: y = 37
х ∙ 15 = 0
х = 0 : 15
х = 0
Проверка:
0 * 15 = 0
0 = 0
Ответ: х = 0
х ∙ 18 = 18
х = 18 : 18
х = 1
Проверка:
1 * 18 = 18
18 = 18
Ответ: х = 1
Если из числа вычесть само себя, то получится нуль.
Если к числу прибавить нуль, то получится это же число.
Если число разделить на само себя, то получается 1.
Если число разделить на 1, то получится это же число.
Если при умножении числа на другое число получается нуль, то одно из чисел равно нулю.
Если число умножить на 1, то получится само число.
Повтори, как решать уравнения.
Выполняем вычисления с пояснениями.
1. Чтобы найти уменьшаемое, нужно к вычитаемому прибавить разность:
12 + 0 = 12.
Проверка:
12 – 12 = 0
0 = 0
2. Чтобы найти второе слагаемое, нужно из суммы вычесть первое слагаемое:
25 – 25 = 0.
Проверка:
25 + 0 = 25.
25 = 25
3. Чтобы найти делимое, нужно частное умножить на делитель:
108 ∙ 1 = 108.
Проверка:
108 : 108 = 1
1 = 1
4. Чтобы найти делимое, нужно частное умножить на делитель:
37 ∙ 1 = 37.
Проверка:
37 : 1 = 37
37 = 37
5. Чтобы найти первый множитель, нужно произведение разделить на второй множитель:
0 : 15 = 0.
Проверка:
0 ∙ 15 = 0
0 = 0
6. Чтобы найти первый множитель, нужно произведение разделить на второй множитель:
18 : 18 = 1.
Проверка:
1 ∙ 18 = 18
18 = 18
Оформляем задание в тетрадь.
х − 12 = 0
х = 12 + 0
х = 12
Проверка:
12 − 12 = 0
0 = 0
25 + х = 25
х = 25 − 25
х = 0
Проверка:
25 + 0 = 25
25 = 25
х : 108 = 1
х = 108 ∙ 1
х = 108
Проверка:
108 : 108 = 1
1 = 1
у : 1 = 37
у = 37 ∙ 1
у = 37
Проверка:
37 : 1 = 37
37 = 37
х ∙ 15 = 0
х = 0 : 15
х = 0
Проверка:
0 ∙ 15 = 0
0 = 0
х ∙ 18 = 18
х = 18 : 18
х = 1
Проверка:
1 ∙ 18 = 18
18 = 18
Номер 19.
Начерти и вырежи 4 квадрата со стороной 4 см. Составь из них 2 разных прямоугольника и найди периметр и площадь каждого из них.
Ответ:У нас есть 4 квадрата. Найдем сначала площадь одного из них. S квадрата = а ∙ а S квадрата = 4 ∙ 4 = 16 см²

Первый прямоугольник. Его площадь равна 4 площадям квадратов. Значит, S = 4 ∙ 16 = 64 см², или же можно перемножить ширину квадрата (4 см) на длину 4 сторон вместе взятых (16 см) и тоже получится 64 см².
.jpg)
Второй прямоугольник. Его площадь тоже равна 4 площадям квадратов, тоесть: 4 ∙ 16 = 64 см². Или же можно умножить сумму длин двух сторон квадрата (8 см) на сумму длин двух сторон квадрата (8 см) и тоже получится 64 см².
.jpg)
Периметр первого прямоугольника = (4 см + 4 см ∙ 4 см) ∙ 2 = 40 (см) Периметр второго прямоугольника = (4 см + 4 см + 4 см + 4 см) ∙ 2 = 32 (см)
Повтори, какие бывают многоугольники, а также как найти периметр и площадь прямоугольника.
Начертим и вырежем 4 квадрата с заданными сторонами.

У нас есть 4 квадрата. Найдем сначала площадь одного из них.
S квадрата = а ∙ а
S квадрата = 4 ∙ 4 = 16 см²
Составим первый прямоугольник и найдем его периметр и площадь.

Его площадь равна 4 площадям квадратов.
Значит, S = 4 ∙ 16 = 64 см², или же можно перемножить ширину квадрата (4 см) на длину 4 сторон вместе взятых (16 см) и тоже получится 64 см².
Периметр первого прямоугольника = (4 см + 4 см ∙ 4 см) ∙ 2 = 40 (см)
Составим второй прямоугольник и найдем его периметр и площадь.

Его площадь тоже равна 4 площадям квадратов, то есть:
4 ∙ 16 = 64 см².
Или же можно умножить сумму длин двух сторон квадрата (8 см) на сумму длин двух сторон квадрата (8 см) и тоже получится 64 см².
Периметр второго прямоугольника = (4 см + 4 см + 4 см + 4 см) ∙ 2 = 32 (см)
Оформляем задание в тетрадь.
Номер 20.
Рассмотри чертёж и выпиши названия всех треугольников с общей стороной АС; ВС.

Ответ:
Треугольники с общей стороной АС: АСВ, АСD, АСМ. Треугольники с общей стороной ВС: ВСМ, ВСА, ВСD, BCK, BCO.
Повтори, какие бывают треугольники.
Рассмотрим чертеж.
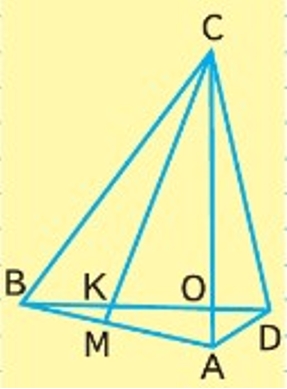
Выпишем названия заданных треугольников.
Треугольники с общей стороной АС: АСВ, АСD, АСМ.
Треугольники с общей стороной ВС: ВСМ, ВСА, ВСD, BCK, BCO.
Номер 21.
1) Объясни, почему на 2 делится без остатка любое число, в записи которого последняя цифра 0, 2, 4, 6 или 8.
2) Какой должна быть последняя цифра в записи числа, которое делится без остатка на 5?
1) Если в записи числа последняя цифра 0, 2, 4, 6 и 8, то это четное число, а все четные числа без остатка делятся на 2. 2) Число, которое без остатка делится на 5, должно на конце записи содержать 0 или 5.
Повтори, что такое деление с остатком.
Ответим на первый вопрос задания.
Если в записи числа последняя цифра 0, 2, 4, 6 и 8, то это четное число, а все четные числа без остатка делятся на 2.
Ответим на второй вопрос задания.
Число, которое без остатка делится на 5, должно на конце записи содержать 0 или 5.
Задание на полях страницы
Найди лишнее выражение.

Ответ:
Лишнее выражение – 120 ∙ 1, потому что это пример на умножение и выполнив действие мы найдем произведение, а все остальные действие на деление и решив их мы найдем частное.
Повтори действия умножение и деление.
Найдем лишнее выражение.
Лишнее выражение – 120 ∙ 1, потому что это пример на умножение и выполнив действие мы найдем произведение, а все остальные действие на деление и решив их мы найдем частное.
Оформим задание в тетрадь.
Номер 3.
Начерти и вырежи 2 таких квадрата (1 и 2). Первый квадрат разрежь на части, как показано на рисунке. Из полученных треугольников и квадрата 2 сложи квадрат 3. Найди его площадь.


Площадь искомого квадрата 1, который разрезали на 4 равных треугольника:
4 см ∙ 4 см = 16 см²
Значит, площадь одного треугольника = 16 : 4 = 4 см².
Площадь квадрата 2 = 2 см ∙ 2 см = 4 см²
Значит площадь построенного квадрата = 4 см² ∙ 4 + 4 см² = 20 см²
Ответ: площадь построенного квадрата составляет 20 см².
Номер 4.
Начерти и вырежи такие же фигуры. Разрежь каждую из них на 2 такие части, которые при наложении совпадут.


Номер 5.
Рассмотри чертёж. Начерти такие же узоры. Раскрась один из них. Сколько осей симметрии у первой фигуры?
Ответ:Смотри! Этот удивительный узор похож на цветочек. Раскрась его так, как тебе нравится. Поделись со взрослыми своим необычным рисунком.

4 оси симметрии у первой фигуры.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.