Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 43
- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Задание вверху страницы
Объясни, как выполнено умножение.
Ответ:Умножение выполнено так, что второй множитель представляется в виде суммы и первый множитель умножается отдельно на каждый из слагаемых, а результаты складываются.
Повтори свойства умножения.
Объясним, как выполнили первый пример.
12 ∙ 15 = 12 ∙ (15 + 5) = 12 ∙ 10 + 12 ∙ 5 = 180
Представим 15 в виде суммы слагаемых 10 и 5, тогда можно 12 сначала умножить на 10, потом на 5, а результаты сложить.
Объясним, как выполнили второй пример.
40 ∙ 32 = 40 ∙ (30 + 2) = 40 ∙ 30 + 40 ∙ 2 = 1 280
Представим 32 в виде суммы слагаемых 30 и 2, тогда можно 40 сначала умножить на 30, потом на 2, а результаты сложить.
Номер 146.
Вычисли с устным объяснением.
Ответ:30 · 16 = 30 · (10 + 6) = 30 · 10 + 30 · 6 = 300 + 180 = 480
Заменю второй множитель суммой удобных слагаемых. Получу выражение: 30 умножить на сумму чисел 10 и 16. Удобнее по правилу умножения числа на сумму умножить число на каждое из слагаемых, а полученные значения сложить. Вычисляю: 300 плюс 180 равно 480. Читаю ответ: произведение чисел 30 и 16 равно 480.
15 · 42 = 15 · (40 + 2) = 15 · 40 + 15 · 2= 600 + 30 = 630
Заменю второй множитель суммой удобных слагаемых. Получу выражение: 15 умножить на сумму чисел 40 и 2. Удобнее по правилу умножения числа на сумму умножить число на каждое из слагаемых, а полученные значения сложить. Вычисляю: 600 плюс 30 равно 630. Читаю ответ: произведение чисел 15 и 42 равно 630.
36 · 11=36 · (10 + 1) = 36 · 10 + 36 · 1 = 360 + 36 = 396
Заменю второй множитель суммой удобных слагаемых. Получу выражение: 36 умножить на сумму чисел 10 и 1. Удобнее по правилу умножения числа на сумму умножить число на каждое из слагаемых, а полученные значения сложить. Вычисляю: 360 плюс 36 равно 396. Читаю ответ: произведение чисел 36 и 11 равно 396.
60 · 42 = 60 · (40 + 2) = 60 · 40 + 60 · 2= 2400 + 120= 2520
Заменю второй множитель суммой удобных слагаемых. Получу выражение: 60 умножить на сумму чисел 40 и 2. Удобнее по правилу умножения числа на сумму умножить число на каждое из слагаемых, а полученные значения сложить. Вычисляю: 2400 плюс 120 равно 2520. Читаю ответ: произведение чисел 60 и 42 равно 2520.
70 · 25 = 70 · (20 + 5) = 70 · 20 + 70 · 5 = 1400 + 350 = 1750
Заменю второй множитель суммой удобных слагаемых. Получу выражение: 70 умножить на сумму чисел 20 и 5. Удобнее по правилу умножения числа на сумму умножить число на каждое из слагаемых, а полученные значения сложить. Вычисляю: 1400 плюс 350 равно 1750. Читаю ответ: произведение чисел 70 и 25 равно 1750.
Повтори таблицу и свойства умножения.
Выполняем вычисления с объяснением.
30 ∙ 16 = 30 ∙ (10 + 6) = 30 ∙ 10 + 30 ∙ 6 = 300 + 180 = 480
Заменю второй множитель суммой удобных слагаемых. Получу выражение: 30 умножить на сумму чисел 10 и 16. Удобнее по правилу умножения числа на сумму умножить число на каждое из слагаемых, а полученные значения сложить. Вычисляю: 300 плюс 180 равно 480. Читаю ответ: произведение чисел 30 и 16 равно 480.
15 ∙ 42 = 15 ∙ (40 + 2) = 15 ∙ 40 + 15 ∙ 2 = 600 + 30 = 630
Заменю второй множитель суммой удобных слагаемых. Получу выражение: 15 умножить на сумму чисел 40 и 2. Удобнее по правилу умножения числа на сумму умножить число на каждое из слагаемых, а полученные значения сложить. Вычисляю: 600 плюс 30 равно 630. Читаю ответ: произведение чисел 15 и 42 равно 630.
36 ∙ 11 = 36 ∙ (10 + 1) = 36 ∙ 10 + 36 ∙ 1 = 360 + 36 = 396
Заменю второй множитель суммой удобных слагаемых. Получу выражение: 36 умножить на сумму чисел 10 и 1. Удобнее по правилу умножения числа на сумму умножить число на каждое из слагаемых, а полученные значения сложить. Вычисляю: 360 плюс 36 равно 396. Читаю ответ: произведение чисел 36 и 11 равно 396.
60 ∙ 42= 60 ∙ (40 + 2) = 60 ∙ 40 + 60 ∙ 2= 2 400 + 120 = 2 520
Заменю второй множитель суммой удобных слагаемых. Получу выражение: 60 умножить на сумму чисел 40 и 2. Удобнее по правилу умножения числа на сумму умножить число на каждое из слагаемых, а полученные значения сложить. Вычисляю: 2400 плюс 120 равно 2520. Читаю ответ: произведение чисел 60 и 42 равно 2520.
70 ∙ 25 = 70 ∙ (20 + 5) = 70 ∙ 20 + 70 ∙ 5 = 1 400 + 350 = 1 750
Заменю второй множитель суммой удобных слагаемых. Получу выражение: 70 умножить на сумму чисел 20 и 5. Удобнее по правилу умножения числа на сумму умножить число на каждое из слагаемых, а полученные значения сложить. Вычисляю: 1400 плюс 350 равно 1750. Читаю ответ: произведение чисел 70 и 25 равно 1750
Оформляем задание в тетрадь.
30 ∙ 16 = 30 ∙ (10 + 6) = 30 ∙ 10 + 30 ∙ 6 = 300 + 180 = 480
15 ∙ 42 = 15 ∙ (40 + 2) = 15 ∙ 40 + 15 ∙ 2 = 600 + 30 = 630
36 ∙ 11 = 36 ∙ (10 + 1) = 36 ∙ 10 + 36 ∙ 1 = 360 + 36 = 396
60 ∙ 42= 60 ∙ (40 + 2) = 60 ∙ 40 + 60 ∙ 2= 2 400 + 120 = 2 520
70 ∙ 25 = 70 ∙ (20 + 5) = 70 ∙ 20 + 70 ∙ 5 = 1 400 + 350 = 1 750
Номер 147.
Выполни действия и сравни приёмы вычислений.
Ответ:
35 ∙ 14 = 35 ∙ (10 + 4) = 35 ∙ 10 + 35 ∙ 4 = 350 + 140 = 490
35 ∙ 40 = 35 ∙ (4 ∙ 10) = (35 ∙ 4) ∙ 10 = 1400
В первом примере второй множитель представляется в виде суммы и первый множитель умножается на каждый из слагаемых. Результаты складываются.
Во втором примере второй множитель представляется в виде произведения и, для удобства умножения, первый множитель умножают на один из получившихся при разложении. Затем результат умножают на оставшийся множитель.
16 ∙ 20 = 16 ∙ (2 ∙ 10) = (16 ∙ 2) ∙ 10 = 320
16 ∙ 12 = 16 ∙ (10 + 2) = 16 ∙ 10 + 16 ∙ 2 = 160 + 32 = 192
В первом примере второй множитель представляется в виде произведения и, для удобства умножения, первый множитель умножают на один из получившихся при разложении. Затем результат умножают на оставшийся множитель.
Во втором примере второй множитель представляется в виде суммы и первый множитель умножается на каждый из слагаемых. Результаты складываются.
Повтори таблицу и свойства умножения.
Выполняем вычисления в первом столбике и сравниваем их.
35 ∙ 14 = 35 ∙ (10 + 4) = 35 ∙ 10 + 35 ∙ 4 = 350 + 140 = 390
35 ∙ 40 = 35 ∙ (4 ∙ 10) = (35 ∙ 4) ∙ 10 = 1400
В первом примере второй множитель представляется в виде суммы и первый множитель умножается на каждый из слагаемых. Результаты складываются.
Во втором примере второй множитель представляется в виде произведения и, для удобства умножения, первый множитель умножают на один из получившихся при разложении. Затем результат умножают на оставшийся множитель.
Выполняем вычисления во втором столбике и сравниваем их.
16 ∙ 20 = 16 ∙ (2 ∙ 10) = (16 ∙ 2) ∙ 10 = 320
16 ∙ 12 = 16 ∙ (10 + 2) = 16 ∙ 10 + 16 ∙ 2 = 160 + 32 = 192
В первом примере второй множитель представляется в виде произведения и, для удобства умножения, первый множитель умножают на один из получившихся при разложении. Затем результат умножают на оставшийся множитель.
Во втором примере второй множитель представляется в виде суммы и первый множитель умножается на каждый из слагаемых. Результаты складываются.
Оформляем задание в тетрадь.
35 ∙ 14 = 35 ∙ (10 + 4) = 35 ∙ 10 + 35 ∙ 4 = 350 + 140 = 390
35 ∙ 40 = 35 ∙ (4 ∙ 10) = (35 ∙ 4) ∙ 10 = 1400
16 ∙ 20 = 16 ∙ (2 ∙ 10) = (16 ∙ 2) ∙ 10 = 320
16 ∙ 12 = 16 ∙ (10 + 2) = 16 ∙ 10 + 16 ∙ 2 = 160 + 32 = 192
Номер 148.
Ответ:70 ∙ 12 = 70 ∙ (10 + 2) = 70 ∙ 10 + 70 ∙ 2 = 840 70 ∙ 20 = 70 ∙ (2 ∙ 10) = (70 ∙ 2) ∙ 10 = 1400 15 ∙ 13 = 15 ∙ (10 + 3) = 15 ∙ 10 + 15 ∙ 3 = 150 + 45 = 195 15 ∙ 30 = 15 ∙ (10 ∙ 3) = (15 ∙ 3) ∙ 10 = 450
Повтори таблицу и свойства умножения.
Выполняем вычисления с пояснением.
Представляем один из множителей в виде суммы двух слагаемых, а затем используем распределительное свойство: при умножении суммы на число можно умножить на него каждое слагаемое в отдельности и полученные результаты сложить.
70 ∙ 12 = 70 ∙ (10 + 2) = 70 ∙ 10 + 70 ∙ 2 = 700 + 140 = 840
70 ∙ 20 = 70 ∙ (10 + 10) = 70 ∙ 10 + 70 ∙ 10 = 700 + 700 = 1 400
15 ∙ 13 = 15 ∙ (10 + 3) = 15 ∙ 10 + 15 ∙ 3 = 150 + 45 = 195
15 ∙ 30 = 15 ∙ (10 + 20) = 15 ∙ 10 + 15 ∙ 20 = 150 + 300 = 450
Оформляем задание в тетрадь.
70 ∙ 12 = 70 ∙ (10 + 2) = 70 ∙ 10 + 70 ∙ 2 = 840
70 ∙ 20 = 70 ∙ (2 ∙ 10) = (70 ∙ 2) ∙ 10 = 1400
15 ∙ 13 = 15 ∙ (10 + 3) = 15 ∙ 10 + 15 ∙ 3 = 150 + 45 = 195
15 ∙ 30 = 15 ∙ (10 ∙ 3) = (15 ∙ 3) ∙ 10 = 450
Номер 149.
Экскаватором можно выкопать за 1 ч канаву длиной 20 м. Одну канаву копали 10 ч, а другую – 12 ч. Найди общую длину канав, которые выкопали за это время. Реши задачу разными способами. Сравни их и выбери самый удобный.
Ответ:
1) 20 ∙ 10 = 200 (м) – длина 1-ой канавы. 2) 20 ∙ 12 = 240 (м) – длина 2-ой канавы. 3) 200 + 240 = 440 (м)
2-й способ решения:1) 10 + 12 = 22 (ч) – общее время. 2) 20 ∙ 22 = 440 (м) Выражение: 20 ∙ (10 + 12) = 440 (м) – составляет длина двух канав
Ответ: 440 м длина двух канав.
Более удобный способ решения данной задачи второй, так как всего два действия.
Длина – величина, характеризующая протяженность объекта на плоскости, выражается в таких единицах измерения, как миллиметр, сантиметр, дециметр, метр, километр.
Помни о соотношении числовых значений единиц измерения длины:
1 см = 10 мм
1 дм = 10 см
1 м = 100 см
1 м = 10 дм
1 км = 1000 м
Шаг 1.
Оформляем условие в виде таблицы.
Рассуждаем.
Найдем длину первой канавы, для этого количество метров, выкопанных за 1 час, умножаем на количество часов работы.
1) 20 ∙ 10 = 200 (м) – длина 1-ой канавы.
Продолжаем рассуждение.
Найдем длину второй канавы, для этого количество метров, выкопанных за 1 час, умножаем на количество часов работы.
2) 20 ∙ 12 = 240 (м) – длина 2-ой канавы.
Продолжаем рассуждение.
Узнаем, сколько метров длина обеих канав, для этого сложим длину каждой канавы вместе.
3) 200 + 240 = 440 (м)
Записываем ответ.
Ответ: 440 м длина двух канав.
Шаг 1.
Рассуждаем.
Найдем общее время копания канав.
1) 10 + 12 = 22 (ч) – общее время.
Продолжаем рассуждение.
Найдем длину двух канав, для этого количество метров, выкопанных за 1 час, умножаем на общее количество часов работы.
2) 20 ∙ 22 = 440 (м)
Записываем ответ.
Ответ: 440 м длина двух канав.
Вывод.
Более удобный способ решения данной задачи второй, так как всего два действия.
Номер 150.
В рыбном хозяйстве в одном пруду вырастили по 7 кг карпа на 1 м2 площади пруда и получили 67200 кг рыбы, а в другом пруду – по 8 кг карпа на 1 м2 площади и получили 61600 кг рыбы. На сколько квадратных метров площадь одного пруда больше площади другого?
Ответ:
Ответ: на 1900 м2 площадь первого пруда больше площади второго пруда.
Площадь – величина, которая характеризует размер части плоскости, занятой фигурой. Измеряется в таких единицах измерения, как: мм2, см2, дм2, м2, км2 и др.
Помни о соотношении числовых значений единиц измерения площади:
1 см2 = 100 мм2
1 дм2 = 100 см2
1 м2 = 10 000 см2
1 м2 = 100 дм2
Оформляем условие в виде таблицы.
Рассуждаем.
Найдем площадь первого пруда.
67 200 : 7 = 9 600 (м2) – площадь первого пруда
Продолжаем рассуждение.
Найдем площадь второго пруда.
61 600 : 8 = 7 700 (м2) – площадь второго пруда
Продолжаем рассуждение.
Найдем разницу между площадью прудов. Для этого из большего значения вычтем меньшее.
9 600 – 7 700 = 1 900 (м2)
Записываем ответ.
Ответ: на 1900 м2 площадь первого пруда больше площади второго пруда.
Оформляем задание в тетрадь.
Ответ: на 1900 м2 площадь первого пруда больше площади второго пруда.
Номер 151.
1) Сколько килограммов в одной десятой части тонны? в одной пятой части центнера?
2) Сколько сантиметров в одной десятой части метра?
1) 1000 : 10 = 100 кг – 10-ая часть тонны. 100 : 5 = 20 кг – 5-ая часть центнера. 2) 100 : 10 = 10 см – 10-ая часть метра.
Повтори единицы массы – тонну и центнер, единицы длины – сантиметр и метр, а также что такое доли.
Рассуждаем.
1 т = 1 000 кг, поэтому одна десятая часть тонны = 1 000 : 10 = 100 кг
1 ц = 100 кг, поэтому одна пятая часть центнера = 100 : 5 = 20 кг
1 м = 100 см, поэтому одна десятая часть метра = 100 : 10 = 10 см
Оформляем задание в тетрадь.
1) 1000 : 10 = 100 кг – 10-ая часть т.
100 : 5 = 20 кг – 5-ая часть ц.
2) 100 : 10 = 10 см – 10-ая часть м.
Номер 152.
1) Сколько квадратных метров в одной второй 1 км2?
2) Сколько квадратных дециметров в одной второй 1 м2?
1) 1000000 : 2 = 500000 м2 2) 100 : 2 = 50 дм2
Повтори единицы площади и что такое доли.
Рассуждаем.
1 км² = 1 000 000 м², значит одна вторая 1 км² = 1 000 000 : 2 = 500 000 м²
1 м² = 100 дм², значит одна вторая 1 м² = 100 : 2 = 50 дм²
Оформляем задание в тетрадь.
1) 1 000 000 : 2 = 500 000 м²
2) 100 : 2 = 50 дм²
Номер 153.
Ответ:
Повтори алгоритм письменного вычитания, умножения и деления многозначных чисел, а также порядок действий.
Выполняем вычисления по действиям.
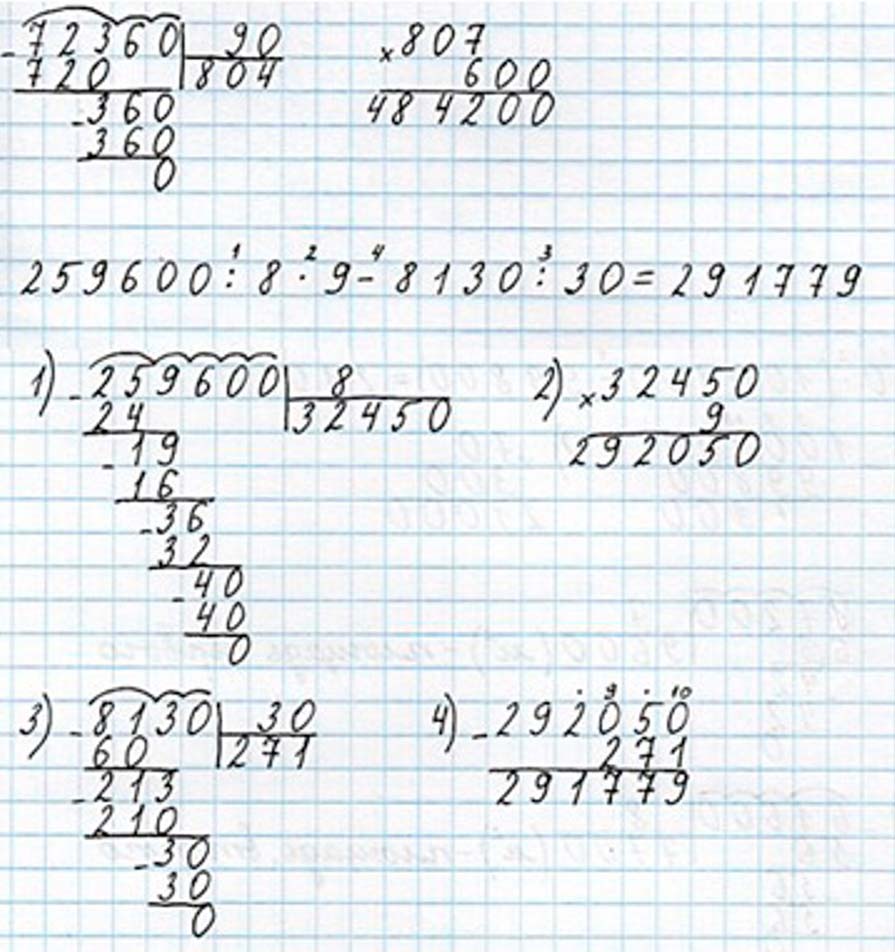
Оформляем задание в тетрадь.
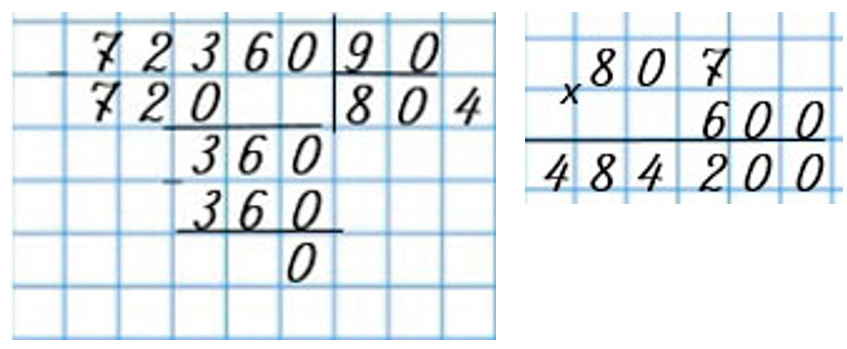
259 600 : 8 ∙ 9 – 8 130 : 30 = 291 779
Номер 154.
Рассмотри круги на рисунках 1 и 2, сравни их по взаимному расположению.
На рис. 1 круги с общим центром.
На рис. 2 круги пересекаются, центр второй окружности находится на окружности первой.
На рис.1 осей симметрии множество. Все они проходят через общий центр кругов и являются диаметрами.
На рис. 2 ось симметрии одна.
Повтори, что такое круг и окружность.
Рассмотрим данные круги.
Сравним.
На рис. 1 круги с общим центром.
На рис. 2 круги пересекаются, центр второй окружности находится на окружности первой.
На рис. 1 осей симметрии множество. Все они проходят через общий центр кругов и являются диаметрами.
На рис. 2 ось симметрии одна.
Номер 155.
Узнай, какое число задумано.
1) Если задуманное число увеличить в 2 раза, а результат увеличить на 20, то получится 120. 2) Если задуманное число уменьшить в 3 раза, а результат уменьшить на 30, то получится 60.
Ответ:
1) (х ∙ 2) + 20 = 120
х ∙ 2 = 120 − 20
х ∙ 2 = 100
х = 100 : 2
х = 50
2) (х : 3) − 30 = 60
х : 3 = 60 + 30
х : 3 = 90
х = 90 ∙ 3
х = 270
Ответ: 1) 50; 2) 270.
Уравнение – равенство с неизвестной, при подстановке числа в которую, получается верное равенство.
Вспомни названия компонентов действия умножения, и зависимость между компонентами и результатом действия умножения:
1 множитель ∙ 2 множитель = значение произведения.
Значение произведения : 1 множитель = 2 множитель.
Значение произведения : 2 множитель = 1 множитель.
Уменьшаемое – вычитаемое = значение разности.
Уменьшаемое – значение разности = вычитаемое.
Значение разности + вычитаемое = уменьшаемое.
Делимое : делитель = значение разности.
Делимое : значение разности = делитель.
Значение разности ∙ делитель = делимое
Выполняем вычисления с пояснением.
Чтобы определить, какое число задумано, обозначаем его буквой и составляем по данным условиям уравнения.
1) (х ∙ 2) + 20 = 120
х ∙ 2 = 120 − 20
х ∙ 2 = 100
х = 100 : 2
х = 50
2) (х : 3) − 30 = 60
х : 3 = 60 + 30
х : 3 = 90
х = 90 ∙ 3
х = 270
Оформляем задание в тетрадь.
1) Задумано число 50.
2) Задумано число 270.
Задание внизу страницы
Ответ:
Повтори алгоритм письменного вычитания, умножения и деления многозначных чисел, а также порядок действий.
Выполняем вычисления по действиям.
Оформляем задание в тетрадь.
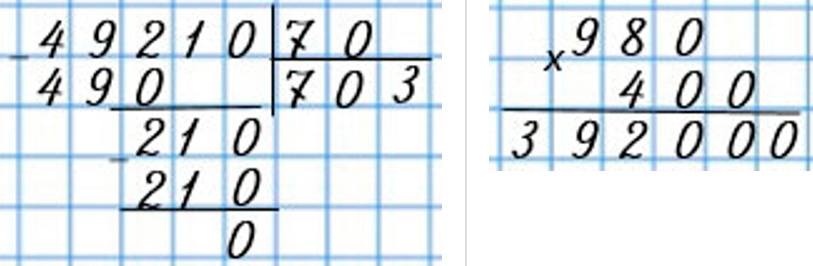
558 720 : 9 ∙ 5 – 6 140 : 20 = 310 093
Задание вверху страницы
Объясни, как выполнено умножение.
Ответ:Умножение выполнено так, что второй множитель представляется в виде суммы и первый множитель умножается отдельно на каждый из слагаемых, а результаты складываются.
1) Повтори таблицу и свойства умножения.
2) Повтори, как умножить число на сумму.
Рассуждаем.
Чтобы умножить число на сумму, можно сначала умножить число на каждое слагаемое, а затем сложить полученные результаты.
12 ∙ 15 = 12 ∙ (10 + 5) = 12 ∙ 10 + 12 ∙ 5 = 120 + 60 = 180
Представим 15 в виде суммы слагаемых 10 и 5, тогда можно 12 сначала умножить на 10, потом на 5, а результаты сложить.
Продолжаем рассуждения.
Чтобы умножить число на сумму, можно сначала умножить число на каждое слагаемое, а затем сложить полученные результаты.
40 ∙ 32 = 40 ∙ (30 + 2) = 40 ∙ 30 + 40 ∙ 2 = 1200 + 80 = 1280
Представим 32 в виде суммы слагаемых 30 и 2, тогда можно 40 сначала умножить на 30, потом на 2, а результаты сложить.
Номер 151.
Вычисли с устным объяснением.
Ответ:30 · 16 = 30 · (10 + 6) = 30 · 10 + 30 · 6 = 300 + 180 = 480
Заменю второй множитель суммой удобных слагаемых. Получу выражение: 30 умножить на сумму чисел 10 и 16. Удобнее по правилу умножения числа на сумму умножить число на каждое из слагаемых, а полученные значения сложить. Вычисляю: 300 плюс 180 равно 480. Читаю ответ: произведение чисел 30 и 16 равно 480.
15 · 42 = 15 · (40 + 2) = 15 · 40 + 15 · 2= 600 + 30 = 630
Заменю второй множитель суммой удобных слагаемых. Получу выражение: 15 умножить на сумму чисел 40 и 2. Удобнее по правилу умножения числа на сумму умножить число на каждое из слагаемых, а полученные значения сложить. Вычисляю: 600 плюс 30 равно 630. Читаю ответ: произведение чисел 15 и 42 равно 630.
36 · 11=36 · (10 + 1) = 36 · 10 + 36 · 1 = 360 + 36 = 396
Заменю второй множитель суммой удобных слагаемых. Получу выражение: 36 умножить на сумму чисел 10 и 1. Удобнее по правилу умножения числа на сумму умножить число на каждое из слагаемых, а полученные значения сложить. Вычисляю: 360 плюс 36 равно 396. Читаю ответ: произведение чисел 36 и 11 равно 396.
60 · 42 = 60 · (40 + 2) = 60 · 40 + 60 · 2= 2400 + 120= 2520
Заменю второй множитель суммой удобных слагаемых. Получу выражение: 60 умножить на сумму чисел 40 и 2. Удобнее по правилу умножения числа на сумму умножить число на каждое из слагаемых, а полученные значения сложить. Вычисляю: 2400 плюс 120 равно 2520. Читаю ответ: произведение чисел 60 и 42 равно 2520.
70 · 25 = 70 · (20 + 5) = 70 · 20 + 70 · 5 = 1400 + 350 = 1750
Заменю второй множитель суммой удобных слагаемых. Получу выражение: 70 умножить на сумму чисел 20 и 5. Удобнее по правилу умножения числа на сумму умножить число на каждое из слагаемых, а полученные значения сложить. Вычисляю: 1400 плюс 350 равно 1750. Читаю ответ: произведение чисел 70 и 25 равно 1750.
1) Повтори таблицу и свойства умножения.
2) Повтори, как умножить число на сумму.
Выполняем вычисления.
30 ∙ 16 = 30 ∙ (10 + 6) = 30 ∙ 10 + 30 ∙ 6 = 300 + 180 = 480
Представим число 16 в виде суммы двух слагаемых 10 и 6. Получим произведение числа и суммы: 30 ∙ (10 + 6).
Чтобы умножить число на сумму, можно сначала умножить число на каждое слагаемое, а затем сложить полученные результаты.
1) 30 ∙ 10 = 300
2) 30 ∙ 6 = 180
3) 300 + 180 = 480
15 ∙ 42 = 15 ∙ (40 + 2) = 15 ∙ 40 + 15 ∙ 2 = 600 + 30 = 630
Представим число 42 в виде суммы двух слагаемых 40 и 4. Получим произведение числа и суммы: 15 ∙ (40 + 2).
Чтобы умножить число на сумму, можно сначала умножить число на каждое слагаемое, а затем сложить полученные результаты.
1) 15 ∙ 40 = 600
2) 15 ∙ 2 = 30
3) 600 + 30 = 630
36 ∙ 11 = 36 ∙ (10 + 1) = 36 ∙ 10 + 36 ∙ 1 = 360 + 36 = 396
Представим число 11 в виде суммы двух слагаемых 10 и 1. Получим произведение числа и суммы: 36 ∙ (10 + 1).
Чтобы умножить число на сумму, можно сначала умножить число на каждое слагаемое, а затем сложить полученные результаты.
1) 36 ∙ 10 = 360
2) 36 ∙ 1 = 36
3) 360 + 36 = 396
60 ∙ 42 = 60 ∙ (40 + 2) = 60 ∙ 40 + 60 ∙ 2 = 2400 + 120 = 2520
Представим число 42 в виде суммы двух слагаемых 40 и 2. Получим произведение числа и суммы: 60 ∙ (40 + 2).
Чтобы умножить число на сумму, можно сначала умножить число на каждое слагаемое, а затем сложить полученные результаты.
1) 60 ∙ 40 = 2400
2) 60 ∙ 2 = 120
3) 2400 + 120 = 2520
70 ∙ 25 = 70 ∙ (20 + 5) = 70 ∙ 20 + 70 ∙ 5 = 1400 + 350 = 1750
Представим число 25 в виде суммы двух слагаемых 20 и 5. Получим произведение числа и суммы: 70 ∙ (20 + 5).
Чтобы умножить число на сумму, можно сначала умножить число на каждое слагаемое, а затем сложить полученные результаты.
1) 70 ∙ 20 = 1400
2) 70 ∙ 5 = 350
3) 1400 + 350 = 1750
Оформляем задание в тетрадь.
30 ∙ 16 = 30 ∙ (10 + 6) = 30 ∙ 10 + 30 ∙ 6 = 300 + 180 = 480
15 ∙ 42 = 15 ∙ (40 + 2) = 15 ∙ 40 + 15 ∙ 2 = 600 + 30 = 630
36 ∙ 11 = 36 ∙ (10 + 1) = 36 ∙ 10 + 36 ∙ 1 = 360 + 36 = 396
60 ∙ 42 = 60 ∙ (40 + 2) = 60 ∙ 40 + 60 ∙ 2 = 2400 + 120 = 2520
70 ∙ 25 = 70 ∙ (20 + 5) = 70 ∙ 20 + 70 ∙ 5 = 1400 + 350 = 1750
Номер 152.
Выполни действия и сравни приёмы вычислений.
Ответ:
35 ∙ 14 = 35 ∙ (10 + 4) = 35 ∙ 10 + 35 ∙ 4 = 350 + 140 = 490
35 ∙ 40 = 35 ∙ (4 ∙ 10) = (35 ∙ 4) ∙ 10 = 1400
В первом примере второй множитель представляется в виде суммы и первый множитель умножается на каждый из слагаемых. Результаты складываются.
Во втором примере второй множитель представляется в виде произведения и, для удобства умножения, первый множитель умножают на один из получившихся при разложении. Затем результат умножают на оставшийся множитель.
16 ∙ 20 = 16 ∙ (2 ∙ 10) = (16 ∙ 2) ∙ 10 = 320
16 ∙ 12 = 16 ∙ (10 + 2) = 16 ∙ 10 + 16 ∙ 2 = 160 + 32 = 192
В первом примере второй множитель представляется в виде произведения и, для удобства умножения, первый множитель умножают на один из получившихся при разложении. Затем результат умножают на оставшийся множитель.
Во втором примере второй множитель представляется в виде суммы и первый множитель умножается на каждый из слагаемых. Результаты складываются.
1) Повтори таблицу и свойства умножения.
2) Повтори, как умножить число на сумму.
3) Повтори, как умножить число на произведение.
Рассуждаем.
35 ∙ 14 = 35 ∙ (10 + 4) = 35 ∙ 10 + 35 ∙ 4 = 350 + 140 = 390
35 ∙ 40 = 35 ∙ (4 ∙ 10) = (35 ∙ 4) ∙ 10 = 140 ∙ 10 = 1400
В первом примере второй множитель представляется в виде суммы и первый множитель умножается на каждый из слагаемых. Результаты складываются.
Во втором примере второй множитель представляется в виде произведения и, для удобства умножения, первый множитель умножают на один из получившихся при разложении. Затем результат умножают на оставшийся множитель.
Продолжаем рассуждения.
16 ∙ 20 = 16 ∙ (2 ∙ 10) = (16 ∙ 2) ∙ 10 = 32 ∙ 10 = 320
16 ∙ 12 = 16 ∙ (10 + 2) = 16 ∙ 10 + 16 ∙ 2 = 160 + 32 = 192
В первом примере второй множитель представляется в виде произведения и, для удобства умножения, первый множитель умножают на один из получившихся при разложении. Затем результат умножают на оставшийся множитель.
Во втором примере второй множитель представляется в виде суммы и первый множитель умножается на каждый из слагаемых. Результаты складываются.
Оформляем задание в тетрадь.
35 ∙ 14 = 35 ∙ (10 + 4) = 35 ∙ 10 + 35 ∙ 4 = 350 + 140 = 390
35 ∙ 40 = 35 ∙ (4 ∙ 10) = (35 ∙ 4) ∙ 10 = 140 ∙ 10 = 1400
16 ∙ 20 = 16 ∙ (2 ∙ 10) = (16 ∙ 2) ∙ 10 = 32 ∙ 10 = 320
16 ∙ 12 = 16 ∙ (10 + 2) = 16 ∙ 10 + 16 ∙ 2 = 160 + 32 = 192
Номер 153.
Ответ:70 ∙ 12 = 70 ∙ (10 + 2) = 70 ∙ 10 + 70 ∙ 2 = 840 70 ∙ 20 = 70 ∙ (2 ∙ 10) = (70 ∙ 2) ∙ 10 = 1400 15 ∙ 13 = 15 ∙ (10 + 3) = 15 ∙ 10 + 15 ∙ 3 = 150 + 45 = 195 15 ∙ 30 = 15 ∙ (10 ∙ 3) = (15 ∙ 3) ∙ 10 = 450
1) Повтори таблицу и свойства умножения.
2) Повтори, как умножить число на сумму.
3) Повтори, как умножить число на произведение.
Выполняем вычисления.
Чтобы умножить число на сумму, можно сначала умножить число на каждое слагаемое, а затем сложить полученные результаты.
70 ∙ 12 = 70 ∙ (10 + 2) = 70 ∙ 10 + 70 ∙ 2 = 700 + 140 = 840
Представим число 12 в виде суммы двух слагаемых 10 и 2. Затем число 30 умножим на каждое из этих слагаемых, а полученные результаты сложим.
Чтобы умножить число на произведение, можно сначала умножить число на один из множителей, а затем полученный результат умножить на другой множитель.
70 ∙ 20 = 70 ∙ (2 ∙ 10) = (70 ∙ 2) ∙ 10 = 140 ∙ 10 = 1400
Представим число 20 в виде произведения двух множителей 2 и 10. Затем число 70 умножим на первый множитель, а полученный результат умножим на второй множитель.
Чтобы умножить число на сумму, можно сначала умножить число на каждое слагаемое, а затем сложить полученные результаты.
15 ∙ 13 = 15 ∙ (10 + 3) = 15 ∙ 10 + 15 ∙ 3 = 150 + 45 = 195
Представим число 13 в виде суммы двух слагаемых 10 и 3. Затем число 15 умножим на каждое из этих слагаемых, а полученные результаты сложим.
Чтобы умножить число на произведение, можно сначала умножить число на один из множителей, а затем полученный результат умножить на другой множитель.
15 ∙ 30 = 15 ∙ (10 ∙ 3) = (15 ∙ 3) ∙ 10 = 45 ∙ 10 = 450
Представим число 30 в виде произведения двух множителей 3 и 10. Затем число 15 умножим на первый множитель, а полученный результат умножим на второй множитель.
Оформляем задание в тетрадь.
70 ∙ 12 = 70 ∙ (10 + 2) = 70 ∙ 10 + 70 ∙ 2 = 700 + 140 = 840
70 ∙ 20 = 70 ∙ (2 ∙ 10) = (70 ∙ 2) ∙ 10 = 140 ∙ 10 = 1400
15 ∙ 13 = 15 ∙ (10 + 3) = 15 ∙ 10 + 15 ∙ 3 = 150 + 45 = 195
15 ∙ 30 = 15 ∙ (10 ∙ 3) = (15 ∙ 3) ∙ 10 = 45 ∙ 10 = 450
Номер 154.
Экскаватором можно выкопать за 1 ч канаву длиной 20 м. Одну канаву копали 10 ч, а другую – 12 ч. Найди общую длину канав, которые выкопали за это время. Реши задачу разными способами. Сравни их и выбери самый удобный.
1) 20 ∙ 10 = 200 (м) – длина 1-ой канавы. 2) 20 ∙ 12 = 240 (м) – длина 2-ой канавы. 3) 200 + 240 = 440 (м)
2-й способ решения:1) 10 + 12 = 22 (ч) – общее время. 2) 20 ∙ 22 = 440 (м) Выражение: 20 ∙ (10 + 12) = 440 (м) – составит длина двух каналов
Ответ: 440 м длина двух канав.
Более удобный способ решения данной задачи второй, так как всего два действия.
1) Длина – величина, характеризующая протяженность объекта на плоскости.
2) Помни о соотношении числовых значений единиц измерения длины.
Шаг 1.
Оформляем условие в виде таблицы.
Рассуждаем.
Найдем длину первой канавы, для этого количество метров, выкопанных за 1 час, умножаем на количество часов работы.
20 ∙ 10 = 200 (м) – длина 1-ой канавы.
Продолжаем рассуждение.
Найдем длину второй канавы, для этого количество метров, выкопанных за 1 час, умножаем на количество часов работы.
20 ∙ 12 = 240 (м) – длина 2-ой канавы.
Продолжаем рассуждение.
Узнаем, сколько метров длина обеих канав, для этого сложим длину каждой канавы вместе.
200 + 240 = 440 (м) – общая длина канав.
Записываем ответ.
Ответ: 440 м длина двух канав.
Шаг 1.
Рассуждаем.
Найдем общее время, за которое выкопали обе канавы.
10 + 12 = 22 (ч) – общее время.
Продолжаем рассуждение.
Найдем длину двух канав, для этого количество метров, выкопанных за 1 час, умножаем на общее количество часов работы.
20 ∙ 22 = 440 (м) – общая длина канав.
Записываем ответ.
Ответ: 440 м длина двух канав.
Делаем вывод.
Более удобный способ решения данной задачи второй, так как всего два действия.
Номер 155.
В рыбном хозяйстве в одном пруду вырастили по 7 кг карпа на 1 м2 площади пруда и получили 67200 кг рыбы, а в другом пруду – по 8 кг карпа на 1 м2 площади и получили 61600 кг рыбы. На сколько квадратных метров площадь одного пруда больше площади другого?
Ответ:
Ответ: на 1900 м2 площадь первого пруда больше площади второго пруда.
1) Площадь – величина, которая характеризует размер части плоскости, занятой фигурой.
2) Помни о соотношении числовых значений единиц измерения площади.
Оформляем условие в виде таблицы.
Рассуждаем.
Найдем площадь первого пруда.
67200 : 7 = 9600 (м2) – площадь первого пруда.
Продолжаем рассуждение.
Найдем площадь второго пруда.
61600 : 8 = 7700 (м2) – площадь второго пруда.
Продолжаем рассуждение.
Узнаем, на сколько площадь одного пруда больше площади другого. Для этого из большего значения вычтем меньшее.
9600 – 7700 = 1900 (м2) – на столько больше.
Записываем ответ.
Ответ: на 1900 м2 площадь одного пруда больше площади другого пруда.
Номер 156.
1) Сколько килограммов в одной десятой части тонны? в одной пятой части центнера? 2) Сколько сантиметров в одной десятой части метра?
Ответ:1) 1000 : 10 = 100 кг – 10-ая часть т. 100 : 5 = 20 кг – 5-ая часть ц. 2) 100 : 10 = 10 см – 10-ая часть м.
Повтори единицы массы – тонну и центнер, единицы длины – сантиметр и метр, а также что такое доли.
Рассуждаем.
Чтобы узнать, сколько килограмм в одной десятой части тонны, нужно перевести тонну в килограммы и разделить на 10 частей.
1 т = 1000 кг
1000 : 10 = 100 (кг) – в одной десятой части тонны.
Чтобы узнать, сколько килограмм в одной пятой части центнера, нужно перевести центнер в килограммы и разделить на 5 частей.
1 ц = 100 кг
100 : 5 = 20 (кг) – в одной пятой части центнера.
Продолжаем рассуждения.
Чтобы узнать, сколько сантиметров в одной десятой части метра, нужно перевести метр в сантиметры и разделить на 10 частей.
1 м = 100 см
100 : 10 = 10 (см) – в одной десятой части метра.
Оформляем задание в тетрадь.
1) 1000 : 10 = 100 (кг) – в одной десятой части тонны.
100 : 5 = 20 (кг) – в одной пятой части центнера.
2) 100 : 10 = 10 (см) – в одной десятой части метра.
Номер 157.
1) Сколько квадратных метров в одной второй 1 км2? 2) Сколько квадратных дециметров в одной второй 1 м2?
Ответ:1) 1000000 : 2 = 500000 м2 2) 100 : 2 = 50 дм2
Повтори единицы площади, и что такое доли.
Рассуждаем.
Чтобы узнать, сколько квадратных метров в одной второй 1 км², нужно перевести квадратный километр в квадратные метры и разделить на 2 части.
1 км² = 1000000 м²,
1000000 : 2 = 500000 (м²) – в одной второй 1 км².
Продолжаем рассуждения.
Чтобы узнать, сколько квадратных дециметров в одной второй 1 м², нужно перевести квадратный метр в квадратные дециметры и разделить на 2 части.
1 м² = 100 дм²
100 : 2 = 50 (дм²) – в одной второй 1 м².
Оформляем задание в тетрадь.
1) 1000000 : 2 = 500000 м²
2) 100 : 2 = 50 дм²
Номер 158.
Ответ:
Повтори алгоритм письменного вычитания, умножения и деления многозначных чисел, а также порядок действий.
Выполняем вычисления.
72360 : 90 = 7236 : 9 = (7200 + 36) : 9 = 800 + 4 = 804
Если делитель и делимое оканчиваются нулями, то можно опустить одинаковое количество нулей.
807 ∙ 600 = 484200
Чтобы умножить число 807 на число 600, достаточно число 807 умножить на 6 и к полученному результату справа дописать два нуля.
259600 : 8 ∙ 9 – 8130 : 30 = 291779
В данном выражении сначала необходимо выполнить действия второй ступени по порядку: деление, умножение и снова деление. А затем нужно выполнить вычитание.
1) 259600 : 8 = 32450
2) 32450 ∙ 9 = 292050
3) 8130 : 30 = 271
4) 292050 – 271 = 291779
Оформляем задание в тетрадь.
Номер 159.
Рассмотри круги на рисунках 1 и 2. По каким признакам круги на рисунках 1 и 2 похожи? По каким различаются?
На рис. 1 круги с общим центром.
На рис. 2 круги пересекаются, центр второй окружности находится на окружности первой.
На рис.1 осей симметрии множество. Все они проходят через общий центр кругов и являются диаметрами.
На рис. 2 ось симметрии одна.
Повтори, что такое круг и окружность.
Рассмотрим круги на рисунках.
Рассуждаем.
На рисунке 1 круги с общим центром.
На рисунке 2 круги пересекаются, центр второй окружности находится на окружности первой.
Продолжаем рассуждения.
На рисунке 1 осей симметрии множество. Все они проходят через общий центр кругов и являются диаметрами.
На рисунке 2 ось симметрии одна.
Номер 160.
Узнай, какое число задумано.
1) Если задуманное число увеличить в 2 раза, а результат увеличить на 20, то получится 120. 2) Если задуманное число уменьшить в 3 раза, а результат уменьшить на 30, то получится 60.
Ответ:
1) (х ∙ 2) + 20 = 120
х ∙ 2 = 120 − 20
х ∙ 2 = 100
х = 100 : 2
х = 50
2) (х : 3) − 30 = 60
х : 3 = 60 + 30
х : 3 = 90
х = 90 ∙ 3
х = 270
1) Уравнение – равенство с неизвестной, при подстановке числа в которую, получается верное равенство.
2) Вспомни названия компонентов действия умножения, и зависимость между компонентами и результатом действия умножения.
Выполняем вычисления.
Чтобы определить, какое число задумано, обозначаем его буквой и составляем по данным условиям уравнения.
Пусть х – задуманное число. Если увеличим его в 2 раза, а к полученному результату прибавим 20, то получим 120.
(х ∙ 2) + 20 = 120
х ∙ 2 = 120 − 20
х ∙ 2 = 100
х = 100 : 2
х = 50 – задуманное число.
Пусть х – задуманное число. Если уменьшим его в 3 раза, а от полученного результата отнимем 30, то получим 60.
(х : 3) − 30 = 60
х : 3 = 60 + 30
х : 3 = 90
х = 90 ∙ 3
х = 270 – задуманное число.
Оформляем задание в тетрадь.
(х ∙ 2) + 20 = 120
х ∙ 2 = 120 − 20
х ∙ 2 = 100
х = 100 : 2
х = 50 – задуманное число.
(х : 3) − 30 = 60
х : 3 = 60 + 30
х : 3 = 90
х = 90 ∙ 3
х = 270 – задуманное число.
Задание внизу страницы
Ответ:
Повтори алгоритм письменного вычитания, умножения и деления многозначных чисел, а также порядок действий.
Выполняем вычисления.
49210 : 70 = 4921 : 7 = (4900 + 21) : 7 = 700 + 3 = 703
Если делитель и делимое оканчиваются нулями, то можно опустить одинаковое количество нулей.
980 ∙ 400 = 392000
Чтобы умножить число 980 на число 400, достаточно число 98 умножить на 4 и к полученному результату справа дописать три нуля.
558720 : 9 ∙ 5 – 6140 : 20 = 310093
В данном выражении сначала необходимо выполнить действия второй ступени по порядку: деление, умножение и снова деление. А затем нужно выполнить вычитание.
1) 558720 : 9 = 62080
2) 62080 ∙ 5 = 310400
3) 6140 : 20 = 307
4) 310400 – 307 = 310093
Оформляем задание в тетрадь.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽
Напишите свой комментарий.