Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 24

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Странички для любознательных
Верно? Неверно?
Номер 1.
Велосипедист за 3 ч проехал 24 км, значит, он ехал со скоростью 8 км/ч.
Ответ:Верно. Скоростью велосипедиста 8 км/ч, потому что 24 км : 3 = 8 км/ч.
Чтобы определить верно ли данное высказывание, нужно его проверить, решив задание.
Проверяем правильность высказывания.
Чтобы найти скорость нужно расстояние разделить на время.
24 : 3 = 8 (км/ч) – скорость велосипедиста.
Делаем вывод.
Данное высказывание верно.
Номер 2.
16000 ∙ 20 = 32000
Ответ:Неверно 16 000 · 20 = 320 000.
Чтобы определить верно ли данное высказывание, нужно его проверить, решив задание.
Проверяем правильность высказывания.
16 000 ∙ 20 = 32 000 – неверно
16 000 ∙ 20 = 320 000 – верно
Делаем вывод.
Данное высказывание неверно.
Номер 3.
45 ∙ 8 = 45 ∙ 4 ∙ 4
Ответ:Неверно. 45 ∙ 8 = 45 ∙ 4 ∙ 2, ведь 360 = 360.
Чтобы определить верно ли данное высказывание, нужно его проверить, решив задание.
Проверяем правильность высказывания.
45 ∙ 8 = 45 ∙ 4 ∙ 4
45 ∙ 8 = 45 ∙ 16 – неверно
Делаем вывод.
Данное высказывание неверно.
Номер 4.
25 ∙ 18 = 25 ∙ 2 ∙ 9
Ответ:Верно.
Чтобы определить верно ли данное высказывание, нужно его проверить, решив задание.
Проверяем правильность высказывания.
25 ∙ 18 = 25 ∙ 2 ∙ 9
25 ∙ 18 = 25 ∙ 18 – верно
Делаем вывод.
Данное высказывание верно.
Номер 5.
В схеме порядок выполнения действий указан правильно.

Ответ:
Неверно. Сначала выполняется действие в скобках, а затем деление и умножение по порядку слева направо.
Чтобы определить верно ли данное высказывание, нужно его проверить, решив задание.
Проверяем правильность высказывания.
При решении данного выражения сначала надо выполнить действия в скобках, а затем по порядку слева направо надо выполнить действие деления и умножения.
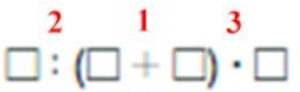
Делаем вывод.
Данное высказывание неверно.
Номер 6.
Если грузоподъёмность прицепа к машине 1 ц, то он сможет за один раз увезти груз массой 150 кг.
Ответ:Неверно. 1 ц = 100 кг
Чтобы определить верно ли данное высказывание, нужно его проверить, решив задание.
Проверяем правильность высказывания.
1 ц = 100 кг
100 кг < 150 кг – значит, увезти за один раз груз 150 кг прицеп не сможет
Делаем вывод.
Данное высказывание неверно.
Номер 7.
Если площадь прямоугольника 100 см², а длина одной его стороны 25 см, то длина другой стороны прямоугольника 4 см.
Ответ:Верно. S = а · b< a = 25 см b = 4 см Значит, 25 · 4 = 100 см2, а 100 см2 = 100 см2
Чтобы определить верно ли данное высказывание, нужно его проверить, решив задание.
Проверяем правильность высказывания.
Чтобы найти площадь прямоугольника нужно длину умножить на ширину.
25 ∙ 4 = 100 (см2) – площадь прямоугольника со сторонами 25 см и 4 см
Делаем вывод.
Данное высказывание верно.
Номер 8.
6899 + 9 ∙ 900 : 8100 = 6900
Ответ:Верно 6899 + 9 · 900 : 8 100 = 6 900 6 899 + 8100 : 8100 = 6900 6899 + 1 = 6900 6900 = 6900
Чтобы определить верно ли данное высказывание, нужно его проверить, решив задание.
Проверяем правильность высказывания.

Делаем вывод.
Данное высказывание верно.
Номер 9.
Периметр прямоугольника со сторонами 2 см и 8 см равен периметру квадрата со стороной 4 см.
Ответ:Неверно. Периметр прямоугольника: (2 + 8) ∙ 2 = 20 (см) Периметр квадрата: 4 ∙ 4 = 16 (см)
Чтобы определить верно ли данное высказывание, нужно его проверить, решив задание.
Проверяем правильность высказывания.
Найдем периметр прямоугольника и квадрата и сравним их.
1) (2 + 8) ∙ 2 = 10 ∙ 2 = 20 (см) – периметр прямоугольника со сторонами 2 см и 8 см.
2) 4 ∙ 4 = 16 (см) – периметр квадрата со стороной 4 см.
3) 20 см ≠ 16 см.
Делаем вывод.
Данное высказывание неверно.
Номер 10.
4 ч 40 мин = 440 мин
Ответ:Неверно. 4 ч 40 мин = 4 ∙ 60 + 40 = 240 + 40 = 280 мин.
Чтобы определить верно ли данное высказывание, нужно его проверить, решив задание.
Проверяем правильность высказывания.
Переведем в минуты данные значения и сравним их.
4 ч 40 мин = 440 мин
280 мин ≠ 440 мин
Делаем вывод.
Данное высказывание неверно.
Номер 11.
Задача «В магазин привезли 27 коробок с черешней. Это в 3 раза больше, чем коробок с вишней. Сколько коробок с вишней привезли в магазин?» решается с помощью действия умножения.
Ответ:Неверно Задача решается делением. 27 : 3 = 9.
Чтобы определить верно ли данное высказывание, нужно его проверить, решив задание.
Проверяем правильность высказывания.
Составим к задаче краткую запись, чтобы легче было определить каким действием она решается.

27 : 3 = 9 (шт.) – коробок с вишней привезли в магазин.
Задача решается с помощью действия деления.
Делаем вывод.
Данное высказывание неверно.
Номер 12.
Если площадь квадрата 49 см2, то его периметр 28 см.
Ответ:Верно. Площадь квадрата равна 49 см2, значит, длина стороны равна а см, ведь S = а · а. Р = а · 4, значит, 7 · 4 = 28 см2.
Чтобы определить верно ли данное высказывание, нужно его проверить, решив задание.
Проверяем правильность высказывания.
Найдем длину стороны квадрата и его площадь и сравним.
1) 28 : 4 = 7 (см) – сторона квадрата, периметр которого равен 28 см.
2) 7 ∙ 7 = 49 (см2) – площадь квадрата, периметр которого равен 28 см.
3) 49 см2 = 49 см2.
Делаем вывод.
Данное высказывание верно.
Номер 19.
Запиши 5 чисел, каждое из которых делится без остатка и на 5, и на 9.
Ответ:45, 90, 135, 180, 225.
Вспомни названия компонентов действия деления и зависимости между компонентами и результатом действия деления:
Делимое : делитель = частное
Делимое : частное = делитель
Частное ∙ делитель = делимое
Рассуждаем.
Число, которое без остатка делится на 5 и на 9, это их произведение.
5 ∙ 9 = 45
45 : 5 = 9
45 : 9 = 5
Прибавим к числу 45 число 45, получим число, которое тоже без остатка делится на 5 и на 9.
45 + 45 = 90
90 : 5 = (50 + 40) : 5 = 10 + 8 = 18
90 : 9 = 10
Снова к получившемуся числу прибавим 45, также получим число, которое без остатка делится на 5 и на 9.
90 + 45 = 135
135 : 5 = (100 + 35) : 5 = 20 + 7 = 27
135 : 9 = (90 + 45) : 9 = 10 + 5 = 15
Снова к получившемуся числу прибавим 45, также получим число, которое без остатка делится на 5 и на 9.
135 + 45 = 180
180 : 5 = (150 + 30) : 5 = 30 + 6 = 36
180 : 9 = 20
Снова к получившемуся числу прибавим 45, также получим число, которое без остатка делится на 5 и на 9.
180 + 45 = 225
225 : 5 = (200 + 25) : 5 = 40 + 5 = 45
225 : 9 = (180 + 45) : 9 = 20 + 5 = 25
Оформим задание в тетрадь.
Ответ: 45, 90, 135, 180, 225.
Номер 20.
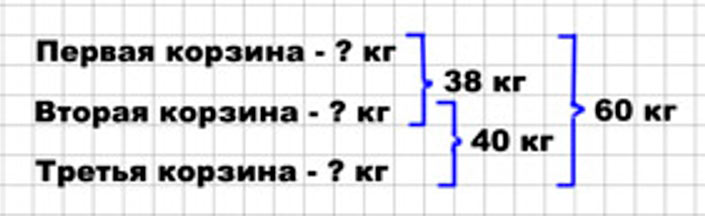
У хозяйки 3 корзины с яблоками. Всего в них 60 кг яблок. В первой и второй корзинах вместе 38 кг яблок, а во второй и третьей вместе 40 кг. Сколько килограммов яблок в каждой корзине?

1) 60 − 38 = 22 (кг) – яблок в третьей корзине.
2) 60 − 40 = 20 (кг) – яблок в первой корзине.
3) 60 − 20 − 22 = 18 (кг) – яблок во второй корзине.
Ответ: масса яблок в первой корзине составляет 20 кг, масса яблок во второй корзине составляет 18 кг, масса яблок третьей корзины составляет 22 кг.
Оформляем условие задачи в виде краткой записи.
Оформляем условие.
Рассуждаем.
Узнаем, сколько яблок в третьей корзине, для этого из всего количества яблок вычтем количество яблок в первой и второй корзинах вместе.
60 − 38 = 22 (кг) – яблок в третьей корзине.
Продолжаем рассуждение.
Узнаем, сколько яблок в первой корзине, для этого из всего количества яблок вычтем количество яблок во второй и третьей корзинах вместе.
60 − 40 = 20 (кг) – яблок в первой корзине.
Продолжаем рассуждение.
Узнаем сколько яблок во второй корзине, для этого из всего количества яблок вычтем количество яблок в первой и третьей корзинах вместе.
60 − 20 − 22 = 18 (кг) – яблок во второй корзине.
Записываем ответ.
Ответ: 20 кг яблок в первой корзине, 18 кг яблок во второй корзине, 22 кг яблок в третьей корзине.
Номер 21.
Ответ:
1) Чтобы умножить число на 10, нужно к нему приписать справа один нуль.
2) Вспомни, как умножать и складывать многозначные числа.
Выполняем вычисления.
2400 ∙ 30 = 24 ∙ 100 ∙ 3 ∙ 10 = 24 ∙ 3 ∙ 1000 = 72000
Достаточно 24 умножить на 3, а нули приписать справа.
24 ∙ 3 = (20 + 4) ∙ 3 = 60 + 12 = 12
450 ∙ 600 = 45 ∙ 10 ∙ 6 ∙ 100 = 45 ∙ 6 ∙ 1000 = 270000
Достаточно 45 умножить на 6, а нули приписать справа.
45 ∙ 6 = (40 + 5) ∙ 6 = 240 + 30 = 270
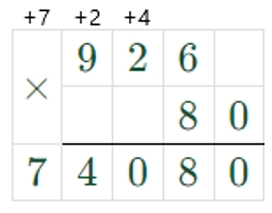
80 ∙ 926 = 926 ∙ 8 ∙ 10 = 74080
200 ∙ 75 = 75 ∙ 2 ∙ 100 = 150 ∙ 100 = 15000
Достаточно 75 умножить на 2, а нули приписать справа.
75 ∙ 2 = (70 + 5) ∙ 2 = 140 + 10 = 150
Выполним вычисления по действиям.
190 ∙ 300 + 929 ∙ 40 = 94160
Сначала выполним умножение по порядку, а затем – сложение.
1) 190 ∙ 300 = 19 ∙ 10 ∙ 3 ∙ 100 = 57000
Достаточно 19 умножить на 3, а нули приписать справа.
19 ∙ 3 = (10 + 9) ∙ 3 = 30 + 27 = 57
2) 929 ∙ 40 = 37160
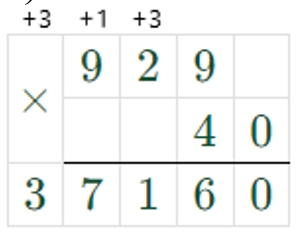
3) 57000 + 37160 = 94160
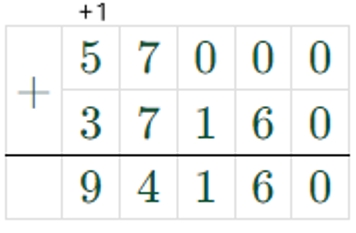
720 ∙ 100 – 28142 : 2 = 72000 – 14071 = 57929
Сначала выполним умножение, затем деление, а потом – вычитание.
1) 720 ∙ 100 = 72000
2) 28142 : 2 =
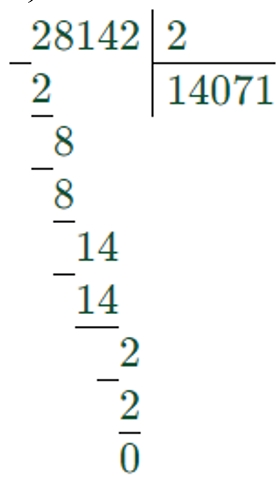
3) 72000 – 14071 = 57929
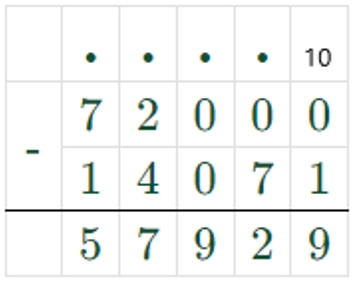
Оформляем задание в тетрадь.
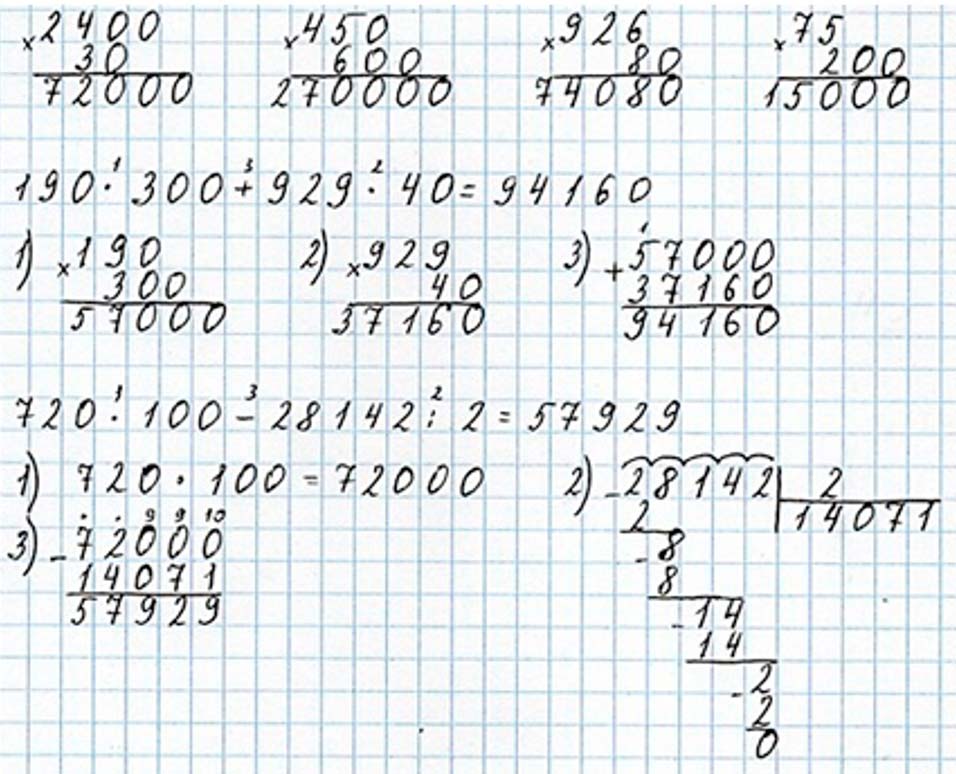
Номер 22.
Ответ:

1) Помни о порядке выполнения арифметических действий, и что скобки влияют на порядок выполнения действий.
2) Вспомни, как умножать и складывать многозначные числа.
Выполняем вычисления.
Выполняем вычисление по действиям.
3000 + (4800 + 1200) : 3 = 5000
Сначала выполняется действие в скобках – сложение, затем – деление, а потом – сложение вне скобок.
1) 4800 + 1200 = 48 сот. + 12 сот. = 60 сот. = 6000
2) 6000 : 3 = 6 тыс. : 3 = 2 тыс. = 2000
3) 3000 + 2000 = 3 тыс. + 2 тыс. = 5 тыс. = 5000
1000 – 900 : 2 + 1600 = 2150
Сначала выполним деление, затем – вычитание, а потом – сложение.
1) 900 : 2 = 90 дес. : 2 = 45 дес. = 450
2) 1000 – 450 = 500 + 500 – 450 = 500 + 50 = 550
3) 550 + 1600 = 500 + 50 + 1500 + 100 = (500 + 1500) + (50 + 100) = 2000 + 150 = 2150
95275 + 2937 ∙ 5 + 374698 = 484658
Сначала выполним умножение, затем – сложение по порядку слева направо.
1) 2937 ∙ 5 = 14685
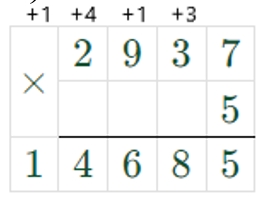
2) 95275 + 14685 = 109960
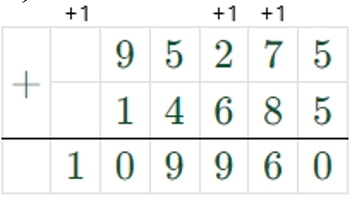
3) 109960 + 374698 = 484658
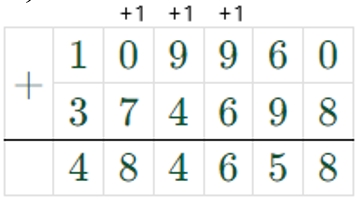
700010 + 190192 : 4 – 8645 = 738913
Сначала выполним деление, затем – сложение, а потом – вычитание.
1) 190192 : 4 = 47548
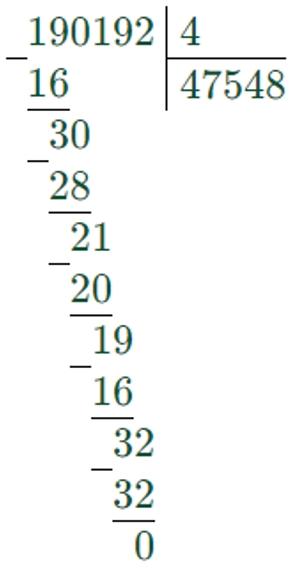
2) 700010 + 47548 = 747558
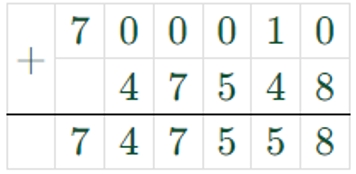
3) 747558 – 8645 = 738913
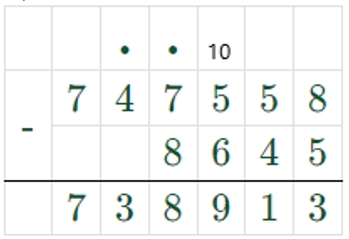
Оформляем задание в тетрадь.

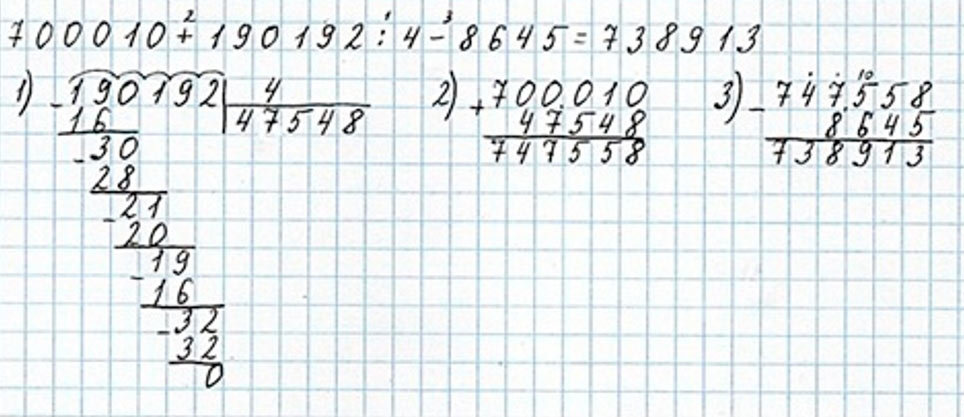
Номер 23.
Вычисли значение выражения а ∙ d, если: 1) а = 8090 и d = 90; 2) а = 108347 и d = 6.
Ответ:1) a ∙ d, если а = 8090, d = 90, то

2) a ∙ d, если а = 108347, d = 6, то

Вспомни, как умножать многозначные числа столбиком.
Выполняем вычисления.
1) Если а = 8090, d = 90, то
a ∙ d = 8090 ∙ 90 = 728100
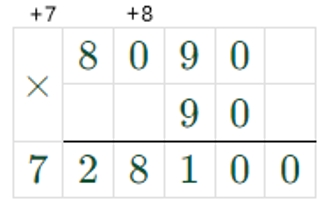
2) Если а = 108347, d = 6, то
a ∙ d = 108347 ∙ 6 = 650082
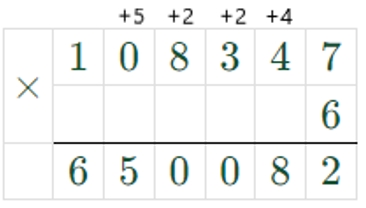
Оформляем задание в тетрадь.
1) a ∙ d = 8090 ∙ 90 = 728100
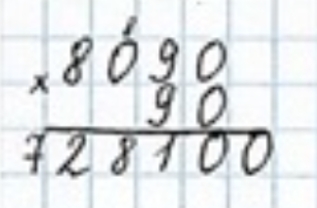
2) a ∙ d = 108347 ∙ 6 = 650082

Номер 24.
Ира задумала число, не равное 0. Увеличила его в 6 раз, результат уменьшила на 40 и получила 200. Какое число задумала Ира? Составь своё похожее задание и предложи другу узнать задуманное число.
Ответ:
Обозначим задуманное число за х, тогда
х · 6 – 40 = 200
х · 6 = 200 + 40
х · 6 = 240
х = 240 : 6
х = 40
Ира задумала число 40.
Ответ: 40.
Задание: Задуманное число, не равное 0, уменьшили в 3 раза, результат увеличили на 60 и получили 110. Узнай задуманное число.
Ответ: Задуманное число – 150.
Уравнение – равенство с неизвестной, при подстановке числа в которую, получается верное равенство.
Рассуждаем.
Ира задумала число, которое не равно нулю.
Обозначим это число за х, составим уравнение и решим его.
х ∙ 6 – 40 = 200
х ∙ 6 = 200 + 40
х ∙ 6 = 240
х = 240 : 6
х = 40 – число, которое задумала Ира.
Записываем ответ.
Ответ: Ира задумала число 40.
Составим задание.
Задуманное число, не равное 0, уменьшили в 3 раза, результат увеличили на 60 и получили 110. Узнай задуманное число.
Рассуждаем.
Обозначим задуманное число за х, составим уравнение и решим его.
х : 3 + 60 = 110
х : 3 = 110 – 60
х : 3 = 50
х = 50 ∙ 3
х = 150 – задуманное число
Записываем ответ.
Ответ: 150 – задуманное число.
Номер 25.
Директор предприятия часто ведёт международные переговоры по телефону. Одна минута разговора с Белоруссией стоит a р., с Францией – а ∙ 3 р., с Китаем – а ∙ 5 р. Состоялось 6 разговоров с Белоруссией, 4 разговора с Францией и 2 разговора с Китаем. Продолжительность каждого разговора 5 мин. Составь различные выражения по этому условию и поясни, что они означают.
Ответ:а ∙ 5 – стоимость одного разговора с Белоруссией. а ∙ 3 ∙ 5 – стоимость одного разговора с Францией. а ∙ 5 ∙ 5 – стоимость одного разговора с Китаем. а ∙ 6 ∙ 5 – стоимость разговоров за месяц с Белоруссией. а ∙ 3 ∙ 4 ∙ 5 – стоимость разговоров за месяц с Францией. а ∙ 5 ∙ 2 ∙ 5 – стоимость разговоров за месяц с Китаем.
Вспомни названия компонентов действия умножения и зависимости между компонентами и результатом действия умножения.
Оформляем краткую запись.
Белоруссия – 6 разговоров, 1 минута – а р.
Франция – 4 разговора, 1 минута – а ∙ 3 р.
Китай – 2 разговора, 1 минута – а ∙ 5 р.
1 разговор – 5 минут
Составляем выражения.
Чтобы узнать стоимость одного разговора, нужно стоимость одной минуты умножить на продолжительность разговора.
Чтобы узнать стоимость разговоров за месяц, нужно стоимость одного разговора умножить на количество разговоров.
а ∙ 5 – стоимость одного разговора с Белоруссией.
а ∙ 3 ∙ 5 – стоимость одного разговора с Францией.
а ∙ 5 ∙ 5 – стоимость одного разговора с Китаем.
а ∙ 5 ∙ 6 – стоимость разговоров за месяц с Белоруссией.
а ∙ 3 ∙ 5 ∙ 4 – стоимость разговоров за месяц с Францией.
а ∙ 5 ∙ 5 ∙ 2 – стоимость разговоров за месяц с Китаем.
Номер 26.
За 6 табуреток заплатили а р., а за 4 стула – b р.
1) Поставь к этому условию два разных вопроса, чтобы задача решалась так: b : 4 − а : 6; (b : 4) : (а : 6).
2) Найди значение каждого выражения при а = 1200 р. и b = 3200 р.
1) b : 4 − a : 6 – на сколько дороже стул табуретки.
(b : 4) : (a : 6) – во сколько раз больше стоит стул, чем табуретка.
2) b : 4 − а : 6 = 3200 : 4 − 1200 : 6 = 800 − 200 = 600
(b : 4) : (a : 6) = (3200 : 4) : (1200 : 6) = 800 : 200 = 4
Вспомни названия компонентов действия умножения и зависимости между компонентами и результатом действия умножения.
Оформляем краткую запись.
6 табуреток – а р.
4 стула – b р.
Рассуждаем.
Чтобы узнать стоимость одной табуретки, нужно сумму, которую заплатили за все табуретки, разделить на количество табуреток.
a : 6 (р.) – стоимость одной табуретки.
Чтобы узнать стоимость одного стула, нужно сумму, которую заплатили за все стулья, разделить на количество стульев.
b : 4 (р.) – стоимость одного стула.
Тогда,
b : 4 − a : 6 (р.) – на сколько стул дороже табуретки;
(b : 4) : (a : 6) (р.) – во сколько раз стул дороже табуретки.
Вычисляем.
Если а = 1200 р. и b = 3200 р., тогда
b : 4 − а : 6 = 3200 : 4 − 1200 : 6 = 800 − 200 = 600 (р.) – на столько стул дороже табуретки.
(b : 4) : (a : 6) = (3200 : 4) : (1200 : 6) = 800 : 200 = 4 (раза) – во столько раз стул дороже табуретки.
Записываем ответ.
1) На сколько стул дороже табуретки?
Во сколько раз стул дороже табуретки?
2) Стул дороже табуретки на 600 рублей.
Стул дороже табуретки в 4 раза.
Номер 27.
Журнал объявил конкурс детских рисунков, в котором приняла участие одна девятая часть его подписчиков. Сколько подписчиков у журнала, если редакция получила рисунки от 10000 детей?
Ответ:
10000 ∙ 9 = 90000 (чел.)
Ответ: 90000 подписчиков у журнала.
Оформляем условие задачи в виде схематического чертежа.
Оформляем условие.
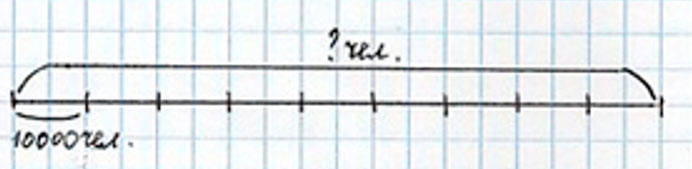
Рассуждаем.
Чтобы узнать, сколько подписчиков у журнала, нужно количество детей, принявших участие в конкурсе, умножить на 9. Так как нам известно, что в конкурсе детских рисунков приняла участие девятая часть от всех подписчиков.
10000 ∙ 9 = 90000 (чел.)
Записываем ответ.
Ответ: 90000 подписчиков у журнала.
Номер 28.
Найди ошибки в решении уравнений.
Ответ:
376 − х = 7 ∙ 9
376 − х = 63
х = 376 − 63
у : 3 = 720 : 9
у = 80 ∙ 3
90 : х = 15 ∙ 6
х = 90 : 90
1) Уравнение – равенство с неизвестной, при подстановке числа в которую, получается верное равенство.
2) Вспомни названия компонентов действия умножения и зависимость между компонентами и результатом действия умножения.
Рассуждаем.
Рассмотрим первое уравнение и решение.
376 − х = 7 ∙ 9
х = 376 + 63
В данном уравнении х – вычитаемое.
Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.
7 ∙ 9 = 63
х = 376 – 63
х = 313
Рассмотрим второе уравнение и решение.
у : 3 = 720 : 9
у = 8 ∙ 3
В данном уравнении у – делимое.
Чтобы найти делимое, нужно делитель умножить на частное.
720 : 9 = 80
у = 80 ∙ 3
у = 240
Рассмотрим третье уравнение и решение.
90 : х = 15 ∙ 6
х = 90 ∙ 90
В данном уравнении х – делитель.
Чтобы найти делитель, нужно делимое разделить на частное.
15 ∙ 6 = 90
х = 90 : 90
х = 1
Оформим задание в тетрадь.
376 − х = 7 ∙ 9
376 − х = 63
х = 376 – 63
х = 313
у : 3 = 720 : 9
у : 3 = 80
у = 80 ∙ 3
у = 240
90 : х = 15 ∙ 6
90 : х = 90
х = 90 : 90
х = 1
Задание на полях страницы
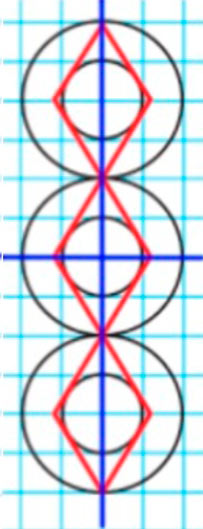
Начерти. Проведи все оси симметрии.
Ответ:
Фигура имеет горизонтальную и вертикальную оси симметрии.
Чтобы проще было перечертить узор, проведи оси симметрии.
Начертим рисунок.
Внимательно рассмотрим узор на полях страницы и с помощью линейки и циркуля начертим его в тетради.
Радиус большой окружности – 2 клетки.
Радиус малой окружности – 1 клетка.
Расстояние между центрами окружностей – 4 клетки.
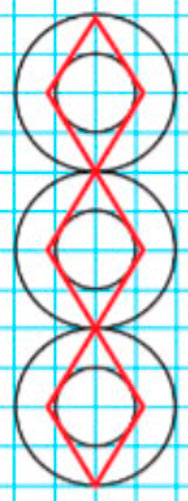
Проведём оси симметрии.
Синим цветом обозначены две оси симметрии: вертикальная и горизонтальная.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.