Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 113
- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Номер 1.
Возьми прямоугольный лист бумаги. Сверни его в трубочку (рис. 1) и склей. Получился предмет, похожий на трубу. Если с двух открытых сторон закрыть кругами, получится модель цилиндра (рис. 2).
Изготовим модель цилиндра: 1) Перечертим на клетчатую бумагу фигуры на рисунке ниже. Это развертка цилиндра. 2) Вырежем ее. 3) Перегнем по красным линиям, намажем клеем “язычки” и склеим.
Если прямоугольный лист бумаги свернуть в трубочку, склеить и с двух открытых сторон закрыть кругами, получится модель цилиндра.
Рассмотрим рисунок.
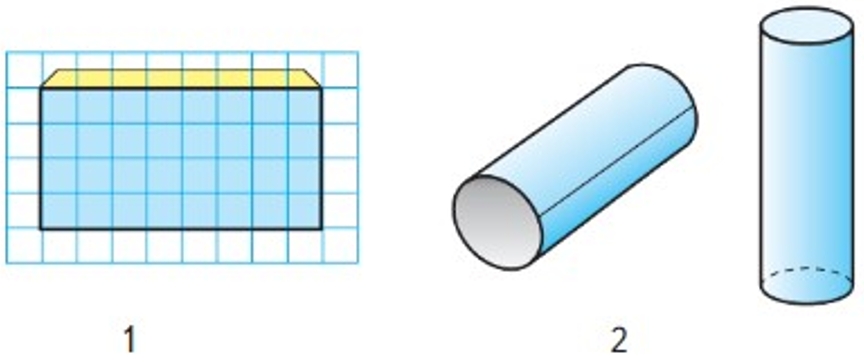
Изготовим модель цилиндра.
1) Перечертим на клетчатую бумагу фигуры на рисунке ниже. Это развертка цилиндра.
2) Вырежем ее.
3) Перегнем по красным линиям, намажем клеем “язычки” и склеим.
Номер 2.
Рассмотри рисунки и назови те предметы, которые имеют форму цилиндра.
Ответ:
На рисунке изображены: банка муки, пачка чая и коробка печенья. Форму цилиндра имеет банка муки и коробка печенья.
Если прямоугольный лист бумаги свернуть в трубочку, склеить и с двух открытых сторон закрыть кругами, получится модель цилиндра.
Рассмотрим рисунок.
Ответим на вопрос.
На рисунке изображены: банка муки, пачка чая и коробка печенья.
Форму цилиндра имеет банка муки и коробка печенья.
Номер 1.
Рассмотри рисунки. Назови нарисованные предметы. Что общего у этих предметов? Все они имеют одинаковую форму – форму шара (рис. 3).
Ответ:
На рисунке изображены: апельсин, арбуз, слепленный шарик. Все эти предметы объединяет то, что они имеют одинаковую форму − форму шара.
Повтори материал о круге.
Рассуждаем и выполняем вычисление.
Ответим на вопрос.
На рисунке изображены: апельсин, арбуз, слепленный шарик.
Все эти предметы объединяет то, что они имеют одинаковую форму − форму шара.
Номер 2.
1) Сравни: квадрат и круг; куб и шар; квадрат и куб; круг и шар.
2) Рассмотри рисунок и разбей фигуры на две группы разными способами.
1) Квадрат и круг.
Квадрат и круг являются симметричными геометрическими фигурами.
У квадрата есть вершины, углы и стороны, а у круга нет.
Куб и шар.
Куб и шар являются геометрическими телами.
У куба есть вершины, грани и ребра, а у шара нет.
Квадрат и куб.
Квадрат − это геометрическая фигура, а куб − это геометрическое тело.
У квадрата есть вершины и стороны, а у куба − вершины, ребра и грани.
Ребра и вершины куба − это стороны и вершины квадратов, из которых он состоит.
Грани куба являются квадратами.
Круг и шар.
Круг − это геометрическая фигура, а объемный, он является геометрическим телом.
У круга и у шара есть радиус и диаметр. Есть центр, от которого равноудалены все точки.
2) Способ 1 (по цвету):
Группа 1 (синие фигуры):
большой куб, малый синий куб и малый шар.
Группа 2 (красные фигуры):
большой шар и малый красный куб.
Способ 2 (по форме):
Группа 1 (кубы):
большой синий куб, малый синий куб, малый красный куб.
Группа 2 (шары):
большой шар и малый шар.
Способ 3 (по размеру):
Группа 1 (большие):
большой синий куб, большой красный шар.
Группа 2 (малые):
малый синий куб, малый красный куб, малый синий шар.
Повтори материал о квадрате и круге.
Рассуждаем и выполняем вычисление.
Выполним задания.
1) Квадрат и круг.
Квадрат и круг являются симметричными геометрическими фигурами.
У квадрата есть вершины, углы и стороны, а у круга нет.
Куб и шар.
Куб и шар являются геометрическими телами.
У куба есть вершины, грани и ребра, а у шара нет.
Квадрат и куб.
Квадрат − это геометрическая фигура, а куб − это геометрическое тело.
У квадрата есть вершины и стороны, а у куба − вершины, ребра и грани.
Ребра и вершины куба − это стороны и вершины квадратов, из которых он состоит.
Грани куба являются квадратами.
Круг и шар.
Круг − это геометрическая фигура, а объемный, он является геометрическим телом.
У круга и у шара есть радиус и диаметр. Есть центр, от которого равноудалены все точки.
2) Способ 1 (по цвету):
Группа 1 (синие фигуры):
большой куб, малый синий куб и малый шар.
Группа 2 (красные фигуры):
большой шар и малый красный куб.
Способ 2 (по форме):
Группа 1 (кубы):
большой синий куб, малый синий куб, малый красный куб.
Группа 2 (шары):
большой шар и малый шар.
Способ 3 (по размеру):
Группа 1 (большие):
большой синий куб, большой красный шар.
Группа 2 (малые):
малый синий куб, малый красный куб, малый синий шар.
Задания повышенного уровня сложности
Номер 1.
Определи, по какому правилу составлена последовательность чисел, и запиши в ней следующее число: 4073, 5075, 6077, 7079, ... .
Ответ:
Каждое последующее число больше предыдущего на 1002.
7079 + 1002 = 8081
Ответ: 4073, 5075, 6077, 7079, 8081.
Повтори состав многозначных чисел.
Рассуждаем.
Каждое последующее число больше предыдущего на 1002.
4073 + 1002 = 5075
5075 + 1002 = 6077
6077 + 1002 = 7079
7079 + 1002 = 8081
Записываем ответ.
Ответ: 4073, 5075, 6077, 7079, 8081.
Номер 2.
В магазин привезли 3 контейнера с овощами: морковью, свёклой и картофелем. Масса контейнера с картофелем 4 т, со свёклой 400 кг, а с морковью 440 кг. Расположи значения массы овощей в порядке их уменьшения.
Ответ:4 т = (4 ∙ 1000) кг = 4000 кг 4000 кг > 440 кг > 400 кг
Повтори единицы массы — тонну и килограмм.
Оформляем краткую запись.
Картофель — 4 т
Свёкла — 400 кг
Морковь — 440 кг
Рассуждаем.
Необходимо расположить значение массы овощей в порядке их уменьшения.
Для этого переведём их в одни единицы массы, в килограммы.
Так как 1 т = 1000 кг, то
4 т = 4000 кг
4000 кг > 440 кг > 400 кг
Номер 3.
Вычисли.
Ответ:
Повтори алгоритм письменного сложения, умножения и деления многозначных чисел, единицы массы — тонну, центнер и килограмм, а также порядок действий.
Выполняем вычисления.
(2846 + 1158) : 28 + 25 ∙ 36 = 1043
В данном выражении сначала выполняется действие в скобках, затем — деление, потом — умножение, а после — сложение.
1) 2846 + 1158 = 4004
2) 4004 : 28 = 143
3) 25 ∙ 36 = 900
4) 143 + 900 = 1043
3 т 8 ц ∙ 3 – 4 ц 90 кг = 10 т 9 ц 10 кг
В данном выражение сначала выполняется действие — умножение, а потом — вычитание.
1) 3 т 8 ц ∙ 3 = 38 ц ∙ 3 = 114 ц = 11 т 4 ц
2) 11 т 4 ц – 4 ц 90 кг = 11 т – 90 кг = 10 т 1000 кг – 90 кг = 10 т 910 кг = 10 т 9 ц 10 кг
Оформляем задание в тетрадь.
Номер 4.
Найди число, которое надо записать в окошко, чтобы равенство 3800 + 48 ∙ ☐ = 7400 стало верным.
Ответ:
Пусть число, которое нужно записать в окошко = х, тогда:
3800 + 48 ∙ х = 7400
48 ∙ х = 7400 − 3800
48 ∙ х = 3600
х = 3600 : 48
х = 75
Проверка:
3800 + 48 ∙ 75 = 7400
3800 + 3600 = 7400
7400 = 7400
Ответ: число, которое нужно записать в окошко равно 75.
Повтори алгоритм вычитания и деления многозначных чисел, а также как решать уравнения.
Рассуждаем.
Пусть х — число, которое нужно записать в окошко, тогда получим уравнение.
3800 + 48 ∙ х = 7400
48 ∙ х = 7400 − 3800
48 ∙ х = 3600
х = 3600 : 48
х = 75
Записываем ответ.
Ответ: число, которое нужно записать в окошко равно 75.
Номер 5.
На дорогу от города до деревни, расстояние между которыми 180 км, мотоциклист затратил 5 ч, а на обратный путь – 6 ч. На сколько меньше была скорость мотоциклиста на обратном пути?
Ответ:
1) 180 : 5 = 36 (км/ч) – скорость мотоциклиста на пути от города до деревни.
2) 180 : 6 = 30 (км/ч) – скорость мотоциклиста на пути от деревни до города.
3) 36 − 30 = 6 (км/ч) – на столько скорость мотоциклиста на обратном пути была меньше, чем его скорость на пути туда.
Ответ: на 6 км/ч скорость мотоциклиста на обратном пути меньше, чем скорость на пути туда.
Повтори взаимосвязь между скоростью, временем и расстоянием.
Оформляем условие в виде таблицы.
Рассуждаем.
Узнаем, какова скорость мотоциклиста на пути от города до деревни.
180 : 5 = 36 (км/ч) — скорость мотоциклиста на пути от города до деревни.
Продолжаем рассуждение.
Узнаем, какова скорость мотоциклиста на пути от деревни до города.
180 : 6 = 30 (км/ч) — скорость мотоциклиста на пути от деревни до города.
Продолжаем рассуждение.
Узнаем, на сколько скорость мотоциклиста на обратном пути была меньше, чем его скорость на пути туда.
36 − 30 = 6 (км/ч) — на столько меньше.
Записываем ответ.
Ответ: на 6 км/ч скорость была меньше.
Номер 6.
На двух полках количество книг сначала было одинаковым. После того как на эти две полки поставили ещё 60 книг, на одной полке стало 65 книг, а на другой – 55 книг. По скольку книг было на каждой полке сначала?
Ответ:
1) 65 + 55 = 120 (кн.) – всего на двух полках.
2) 120 − 60 = 60 (кн.) – было.
3) 60 : 2 = 30 (кн.) – было на каждой полке в начале.
Ответ: 30 книг всего было на каждой полке в начале.
Повтори, как делить круглые числа.
Оформляем условие в виде таблицы.
Рассуждаем.
Узнаем, сколько всего книг стало на двух полках.
65 + 55 = 120 (кн.) — стало на двух полках.
Продолжаем рассуждение.
Узнаем, сколько книг всего было.
120 − 60 = 60 (кн.) — было.
Продолжаем рассуждение.
Узнаем, сколько книг было на каждой полке сначала.
60 : 2 = 30 (кн.) — было на каждой полке.
Записываем ответ.
Ответ: по 30 книг было на каждой полке.
Номер 7.
Школьная экскурсия в соседний город продолжалась двое суток и 5 ч. Ученики вернулись с экскурсии 20 июля в 12 ч дня. Определи, в какой день, месяц и час дети уехали на экскурсию.
Ответ:
1) 20 июля 12 ч − 2 сут. = 18 июля 12 ч
2) 18 июля 12 ч − 5 ч = 18 июля 7 ч − время начала экскурсии.
Ответ: 18 июля в 7 часов утра начнутся школьная экскурсия в соседний город.
Повтори единицы времени — час, сутки и месяц.
Оформляем условие в виде схематического чертежа.
Рассуждаем.
Чтобы узнать, когда дети уехали на экскурсию, нужно из даты вычесть количество суток, а из времени — количество часов.
20 июля – 2 сут. = 18 июля — день и месяц отъезда
12 ч – 5 ч = 7 ч — время отъезда.
Записываем ответ.
Ответ: дети уехали на экскурсию 18 июля в 7 часов утра.
Номер 8.
Реши уравнение и выполни проверку:
Ответ:780 − х = 630 : 9 780 − х = 70 х = 780 − 70 х = 710 Проверка: 780 − 710 = 630 : 9 70 = 70 Ответ: х = 710
Повтори, как решать уравнения.
Рассуждаем.
780 − х = 630 : 9
Для начала вычислим правую часть уравнения.
780 − х = 70
х – неизвестное вычитаемое.
Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.
х = 780 − 70
х = 710
Продолжаем рассуждение.
Чтобы выполнить проверку, нужно найденное значение подставить в уравнение.
780 − 710 = 630 : 9
70 = 70
Номер 9.
Какими могу быть длины сторон прямоугольника в сантиметрах, площадь которого равна площади квадрата со стороной 4 см? Дай два ответа.
Ответ:Площадь квадрата 4 ∙ 4 = 16 см² Длины сторон прямоугольника могут быть: 1 см и 16 см; 2 см и 8 см;
Повтори единицу длины — сантиметр, единицы площади, а также как найти площадь прямоугольника.
Рассуждаем.
Для начала найдём площадь квадрата.
Чтобы вычислить площадь квадрата, нужно умножить его сторону саму на себя
4 ∙ 4 = 16 (см2) — площадь квадрата.
Продолжаем рассуждение.
Чтобы найти площадь прямоугольника, нужно его длину умножить на ширину. Значит, произведение длины и ширины прямоугольника равно 16 см2. Подходят 2 пары чисел:
1 ∙ 16 = 16
2 ∙ 8 = 16
Оформляем задание в тетрадь.
Площадь квадрата 4 ∙ 4 = 16 см²
Длины сторон прямоугольника могут быть:
1 см и 16 см; 2 см и 8 см.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽
Напишите свой комментарий.