Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 100
- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Номер 17.
Вместе 6 ручек и 6 карандашей стоят а р. Ручка стоит k р. Запиши выражения, которые показывают:
1) сколько стоит 1 карандаш;
2) сколько стоят 12 карандашей.
1) (а − 6 ∙ к) : 6 2) (а − 6 ∙ л) : 6 ∙ 12
Повтори взаимосвязь между ценой, количеством и стоимостью.
Рассуждаем.
6 ∙ k – стоимость шести ручек.
a – 6 ∙ k – стоимость шести карандашей.
Чтобы найти стоимость, нужно цену умножить на количество.
Чтобы найти цену, нужно стоимость разделить на количество.
Оформляем задание в тетрадь.
1) (а − 6 ∙ к) : 6
2) (а − 6 ∙ л) : 6 ∙ 12
Номер 18.
Составь по таблице задачу. Используя данные таблицы, запиши выражение, которое обозначает цену люстры.
Для школы закупили 25 светильников по цене b р. за штуку и 8 люстр. Сколько стоит люстра, если стоимость покупок одинаковая?
25 ∙ b : 8 – цена люстры.
Повтори взаимосвязь между ценой, количеством и стоимостью.
Рассмотрим таблицу.
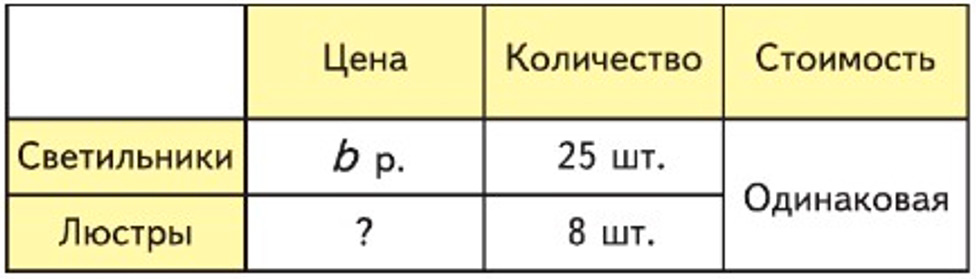
Составим задачу по данным таблицы.
Для школы закупили 25 светильников по цене b р. за штуку и 8 люстр. Сколько стоит люстра, если стоимость покупок одинаковая?
Рассуждаем.
Вычислим, чему равна стоимость люстры.
25 ∙ b : 8 – цена люстры.
Номер 19.
Два разных автомата выпускают каждый по 30000 спичек в минуту и упаковывают их в коробки: один по 50 штук, другой по 60 штук. Какой автомат упаковывает больше коробков спичек в минуту и на сколько коробков больше?
Ответ:
1) 30000 : 50 = 600 (к.) − упаковывает первый автомат.
2) 30000 : 60 = 500 (к.) − упаковывает второй автомат.
3) 600 − 500 = 100 (к.) − на столько больше коробок упаковывает первый автомат, чем второй.
Ответ: на 100 коробок больше упаковывает первый автомат, чем второй.
Оформляем условие задачи в виде таблицы.
Оформляем условие.
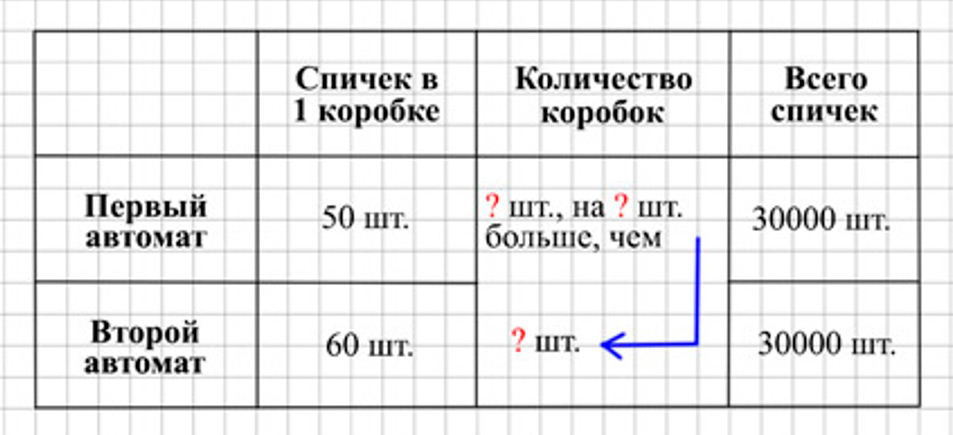
Рассуждаем.
Узнаем, сколько коробок со спичками упаковывает первый автомат.
1) 30000 : 50 = 600 (к.) – упаковывает первый автомат.
Продолжаем рассуждение.
Узнаем, сколько коробок со спичками упаковывает второй автомат.
2) 30000 : 60 = 500 (к.) – упаковывает второй автомат.
Продолжаем рассуждение.
Узнаем, на сколько больше коробок упаковывает первый автомат, чем второй.
3) 600 − 500 = 100 (к.) – на столько больше коробок упаковывает первый автомат, чем второй.
Записываем ответ.
Ответ: на 100 коробок больше.
Номер 20.
Путешественники проплыли на парусной лодке за первые сутки пути 160 км, что на 30 км больше, чем за вторые сутки, и в 2 раза больше, чем за третьи. Сколько всего километров проплыли путешественники за трое суток?
Ответ:
1) 160 − 30 = 130 (км) – проплыли за вторые сутки.
2) 160 : 2 = 80 (км) – проплыли за третьи сутки.
3) 130 + 80 + 160 = 370 (км) – проплыли путешественники за трое суток.
Ответ: 370 км всего проплыли путешественники за трое суток.
Повтори способы оформления краткой записи к задаче, а также единицу длины – километр.
Оформляем условие в виде краткой записи.
Рассуждаем.
Узнаем, сколько км проплыли путешественники за вторые сутки.
1) 160 − 30 = 130 (км) – проплыли за вторые сутки.
Продолжаем рассуждение.
Узнаем, сколько км проплыли путешественники за третьи сутки.
2) 160 : 2 = 80 (км) – проплыли за третьи сутки.
Продолжаем рассуждение.
Узнаем, сколько км проплыли путешественники за трое суток.
3) 130 + 80 + 160 = 370 (км) – проплыли путешественники за трое суток.
Записываем ответ.
Ответ: 370 км.
Номер 21.
Олег проехал на мотороллере 100 км за 3 ч. За сколько часов он может проехать с той же скоростью 200 км?
Ответ:
Проехал на мотороллере 100 км за 3 ч
Проехал на мотороллере 200 км за ? ч
1) 200 : 100 = 2 (раза) – во столько раз больше он проедет, значит и время будет во столько же раз больше.
2) 2 ∙ 3 = 6 (ч) – будет ехать Олег, чтобы проехать 200 км.
Ответ: за 6 часов Олег проедет 200 км.
Повтори взаимосвязь между скоростью, временем и расстоянием.
Оформляем условие в виде краткой записи.
Проехал на мотороллере 100 км за 3 ч
Проехал на мотороллере 200 км за ? ч
Рассуждаем
Узнаем, во сколько раз больше времени затратит Олег на путь 200 км.
1) 200 : 100 = 2 (раза) – во столько раз больше он проедет, значит и время будет во столько же раз больше.
Продолжаем рассуждение.
Вычислим, сколько часов будет ехать Олег, чтобы проехать 200 км.
2) 2 ∙ 3 = 6 (ч) – будет ехать Олег, чтобы проехать 200 км.
Записываем ответ.
Ответ: за 6 часов.
Номер 22.
Два одинаковых насоса выкачивали из подвала воду: первый работал 12 мин, второй – 18 мин, и он выкачал на 4320 л воды больше, чем первый. Сколько литров воды выкачал каждый насос?
Ответ:
2) 4320 : 6 = 720 (л) – воды выкачивает насос за 1 мин.
3) 720 ∙ 18 = 12960 (л) – воды выкачивает второй насос.
4) 720 ∙ 12 = 8640 (л) – воды выкачивает первый насос.
Ответ: 8640 л воды выкачивает первый насос, 12960 л воды выкачивает второй насос.
Повтори единицу времени – минуту и единицу объёма – литр.
Оформляем условие в виде таблицы.
Рассуждаем.
Узнаем, на сколько минут дольше работал второй насос, чем первый.
1) 18 − 12 = 6 (мин) – работал дольше второй насос, чем первый.
Продолжаем рассуждение.
Узнаем, сколько литров воды выкачивает насос за 1 минуту.
2) 4320 : 6 = 720 (л) – воды выкачивает насос за 1 мин.
Продолжаем рассуждение.
Узнаем, сколько литров воды выкачивает второй насос.
3) 720 ∙ 18 = 12960 (л) – воды выкачивает второй насос.
Продолжаем рассуждение.
Узнаем, сколько литров воды выкачивает первый насос.
4) 720 ∙ 12 = 8640 (л) – воды выкачивает первый насос.
Записываем ответ.
Ответ: 8640 л, 12960 л.
Номер 23.
С аэродрома одновременно поднялись два вертолёта, которые полетели в противоположных направлениях. Один из них летел со скоростью 240 км/ч, а другой – 180 км/ч. На каком расстоянии друг от друга будут вертолёты через 3 ч? Реши задачу разными способами.
Ответ:
1) 240 + 180 = 420 (км/ч) – скорость удаления вертолетов. 2) 420 ∙ 3 = 1260 (км) – расстояние между вертолетами через 3 ч.
1) 240 ∙ 3 = 720 (км) – пролетел первый вертолет за 3 ч. 2) 180 ∙ 3 = 540 (км) – пролетел второй вертолет за 3 ч. 3) 720 + 540 = 1260 (км) - расстояние между вертолетами через 3 часа.
Ответ: расстояние между вертолётами через 3 часа составит 1260 км.
Повтори взаимосвязь между скоростью, временем и расстоянием.
Оформляем условие в виде таблицы.
Шаг 1.
Рассуждаем.
Вычислим, чему равна скорость удаления вертолетов.
1) 240 + 180 = 420 (км/ч) – скорость удаления вертолетов.
Продолжаем рассуждение.
Вычислим, чему равно расстояние между вертолетами через 3 часа.
2) 420 ∙ 3 = 1260 (км) – расстояние между вертолетами через 3 ч.
Записываем ответ.
Ответ: 1260 км.
Шаг 1.
Рассуждаем.
Узнаем, сколько км пролетел первый вертолет за 3 часа.
1) 240 ∙ 3 = 720 (км) – пролетел первый вертолет за 3 ч.
Продолжаем рассуждение.
Узнаем, сколько км пролетел второй вертолет за 2 часа.br> 2) 180 ∙ 3 = 540 (км) – пролетел второй вертолет за 2 ч.
Продолжаем рассуждение.
Вычислим, чему равно расстояние между вертолетами через 3 часа.
3) 720 + 540 = 1260 (км) – расстояние между вертолетами через 3 часа.
Записываем ответ.
Ответ: 1260 км.
Задание на полях страницы
Ребус.
Ответ:
Перед нами ребус, для того чтобы найти недостающие цифры необходимо выполнить умножение.
Рассмотрим ребус.
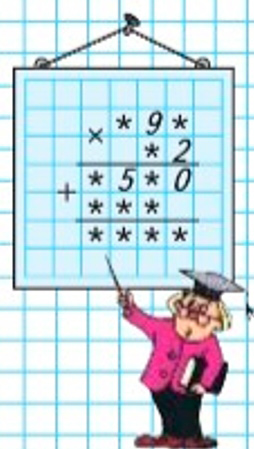
Разгадаем ребус.
Умножаем на единицы. Какое число надо умножить на 2, чтобы в единицах получилось 0? Это число 5. 5 ∙ 2 = 10. 1 дес. запомню и прибавлю к десяткам после умножения десятков.
9 ∙ 2 = 18, да еще 1 дес., который получился при умножении единиц. 18 + 1 = 19. Пишу 9, а 1 запомню и прибавлю к сотням после умножения сотен.
После умножения сотен получилось двузначное число с 5 единицами. 1 сотня оставалась после умножения десятков, значит после умножения на 2 получилось двузначное число с 4 единицами. 7 ∙ 2 = 14.
Умножаем на десятки. После умноженияя числа 795 получилось трехзначное число. Значит, умножали на 1, так как при умножении на большее число получится четырехзначное число. 795 ∙ 1 = 795.
Складываем неполные произведения, получится 9640.
Оформим задание в тетрадь.
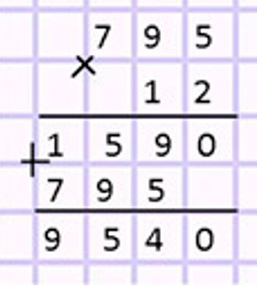
Номер 2.
В телевизионной игре одна женщина выиграла 25000 р. По правилам игры десятую часть своего выигрыша она подарила детской больнице. Сколько рублей она подарила детской больнице?
Ответ:
25000 : 10 = 2500 (р.) – женщина подарила детской больнице.
Ответ: 2500 рублей всего подарила женщина детской больнице.
Повтори способы оформления краткой записи к задаче и денежную единицу — рубль.
Оформляем условие в виде краткой записи.
Рассуждаем.
Чтобы узнать, сколько женщина подарила детской больнице, нужно сумму выигрыша разделить на 10.
25000 : 10 = 2500 (р.) — подарила.
Записываем ответ.
Ответ: 2500 рублей женщина подарила детской больнице.
Номер 3.
Папе 42 года, сыну 7 лет. Во сколько раз папа старше сына?
Ответ:
42 : 7 = 6 (раз) – во столько раз папа старше сына.
Ответ: в 6 раз папа старше сына.
Повтори способы оформления краткой записи к задаче.
Оформляем условие в виде краткой записи.
Рассуждаем.
Чтобы узнать, во сколько раз папа старше сына, нужно возраст папы разделить на возраст сына.
42 : 7 = 6 (раз) — во столько раз старше.
Записываем ответ.
Ответ: в 6 раз папа старше сына.
Номер 4.
Используя данные таблицы, составь и реши задачи, в которых нужно узнать, сколько краски или лака потребуется для покрытия пола комнаты площадью 16 м²; 24 м²; 19 м².
Задача 1:
Пол в трех комнатах площадью 16 м², 24 м², 19 м² нужно покрасить краской в 2 слоя. Расход краски 120 г на 1 м². Сколько краски потребуется для каждой комнаты?
120 ∙ 16 ∙ 2 = 1920 ∙ 2 = 3840 (г) = 3 кг 840 г
120 ∙ 24 ∙ 2 = 2880 ∙ 2 = 5760 (г) = 5 кг 760 г
120 ∙ 19 ∙ 2 = 2280 ∙ 2 = 4560 (г) = 4 кг 560 г
Ответ: 3 кг 840 г краски потребуется для покраски первой комнаты, 5 кг 760 г краски потребуется для покраски второй комнаты, 4 кг 560 г краски потребуется для покраски третьей комнаты.
Задача 2:
В трёх комнатах решили покрыть лаком пол в 3 слоя. Площадь одной комнаты 24 м², другой 19 м² и третьей 16 м². Расход лака составляет 100 г на 1 м². Сколько лака нужно купить для каждой комнаты?
24 ∙ 100 ∙ 3 = 2400 ∙ 3 = 7200 (г) = 7 кг 200 г
19 ∙ 100 ∙ 3 = 1900 ∙ 3 = 5700 (г) = 5 кг 700 г
16 ∙ 100 ∙ 3 = 1600 ∙ 3 = 4800 (г) = 4 кг 800 г
Ответ: 7 кг 200 г лака нужно для покраски пола первой комнаты, 5 кг 700г лака нужно для покраски пола второй полки, 4 кг 800 г лака нужно для покраски пола третьей комнаты.
Повтори единицы массы — килограмм и грамм и единицы площади.
Шаг 1.
Составим первую задачу.
Пол в трех комнатах площадью 16 м², 24 м², 19 м² нужно покрасить краской в 2 слоя. Расход краски 120 г на 1 м². Сколько краски потребуется для каждой комнаты?
Рассуждаем.
Узнаем, сколько краски потребуется для комнаты площадью 16 м².
120 ∙ 16 ∙ 2 = 1920 ∙ 2 = 3840 (г) = 3 кг 840 г
Продолжаем рассуждение.
Узнаем, сколько краски потребуется для комнаты площадью 24 м².
120 ∙ 24 ∙ 2 = 2880 ∙ 2 = 5760 (г) = 5 кг 760 г
Продолжаем рассуждение.
Узнаем, сколько краски потребуется для комнаты площадью 19 м².
120 ∙ 19 ∙ 2 = 2280 ∙ 2 = 4560 (г) = 4 кг 560 г
Записываем ответ.
Ответ: 3 кг 840 г, 5 кг 760 г, 4 кг 560 г.
Шаг 1.
Составим вторую задачу.
В трёх комнатах решили покрыть лаком пол в 3 слоя. Площадь одной комнаты 24 м², другой 19 м² и третьей 16 м². Расход лака составляет 100 г на 1 м². Сколько лака нужно купить для каждой комнаты?
Рассуждаем.
Узнаем, сколько краски потребуется для комнаты площадью 16 м².
16 ∙ 100 ∙ 3 = 1600 ∙ 3 = 4800 (г) = 4 кг 800 г
Продолжаем рассуждение.
Узнаем, сколько краски потребуется для комнаты площадью 24 м².
24 ∙ 100 ∙ 3 = 2400 ∙ 3 = 7200 (г) = 7 кг 200 г
Продолжаем рассуждение.
Узнаем, сколько краски потребуется для комнаты площадью 19 м².
19 ∙ 100 ∙ 3 = 1900 ∙ 3 = 5700 (г) = 5 кг 700 г
Записываем ответ.
Ответ: 7 кг 200 г, 5 кг 700г, 4 кг 800 г.
Номер 5.
Начерти план каждого участка и покажи на нём те объекты, о которых говорится в задачах.
1) Длина прямоугольного поля 500 м, а ширина на 220 м меньше. Седьмую часть этого поля занимает овёс, одну вторую часть – пшеница, а остальную площадь – рожь. Какую площадь занимает рожь?
2) Площадь садового участка 600 м². На нём стоит дом длиной 6 м и шириной 4 м. Из остальной площади участка одну третью часть отвели под сад, а одну четвёртую – под огород. Сколько свободного места осталось на этом участке?
Задача 1:
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 100, номер 5, задача 1, 2024 год.")
1) 500 − 220 = 280 (м) – ширина поля.
2) 500 ∙ 280 = 140000 (м²) – площадь поля.
3) 140000 : 7 = 20000 (м²) – занято овсом.
4) 140000 : 2 = 70000 (м²) – занято пшеницей.
5) 20000 + 70000 = 90000 (м²) – занято овсом и пшеницей.
6) 140000 − 90000 = 50000 (м²) – занято рожью.
Ответ: площадь, занятая рожью составляет 50000 м².
Задача 2:
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 100, номер 5, задача 2, 2024 год.")
1) 6 ∙ 4 = 24 (м²) – площадь дома.
2) 600 − 24 = 576 (м²) – площадь без учета дома.
3) 576 : 3 = 192 (м²) – сад.
4) 576 : 4 = 144 (м²) – огород.
5) 192 + 144 + 24 = 360 (м²) – занято.
6) 600 − 360 = 240 (м²) – свободно.
Ответ: свободная площадь составляет 240 м².
Повтори единицу длины — метр, единицы площади, что такое доли, а также как найти площадь прямоугольника.
Шаг 1.
Оформляем условие в виде краткой записи.
Рассуждаем.
Узнаем, чему равна ширина поля.
500 − 220 = 280 (м) — ширина поля.
Продолжаем рассуждение.
Узнаем, чему равна площадь поля.
500 ∙ 280 = 140000 (м²) — площадь поля.
Продолжаем рассуждение.
Узнаем, сколько м² занято овсом.
140000 : 7 = 20000 (м²) — занято овсом.
Продолжаем рассуждение.
Узнаем, сколько м² занято пшеницей.
140000 : 2 = 70000 (м²) — занято пшеницей.
Продолжаем рассуждение.
Узнаем, сколько м² занято овсом и пшеницей.
20000 + 70000 = 90000 (м²) — занято овсом и пшеницей.
Продолжаем рассуждение.
Узнаем, сколько м² занято рожью.
140000 − 90000 = 50000 (м²) — занято рожью.
Записываем ответ.
Ответ: 50000 м² занято рожью.
Шаг 1.
Оформляем условие в виде краткой записи.
Рассуждаем.
Вычислим, чему равна площадь дома.
6 ∙ 4 = 24 (м²) — площадь дома.
Продолжаем рассуждение.
Вычислим, чему равна площадь без учета дома.
600 − 24 = 576 (м²) — площадь без учета дома.
Продолжаем рассуждение.
Узнаем, сколько м² занимает сад.
576 : 3 = 192 (м²) — занимает сад.
Продолжаем рассуждение.
Узнаем, сколько м² занимает огород.
576 : 4 = 144 (м²) — занимает огород.
Продолжаем рассуждение.
Узнаем, сколько м² занято.
192 + 144 + 24 = 360 (м²) — всего занято.
Продолжаем рассуждение.
Узнаем, сколько м² свободно.
600 − 360 = 240 (м²) — свободно.
Записываем ответ.
Ответ: 240 м² свободно.
Номер 6.
Площадь огорода 500 м². На каждый квадратный метр площади высаживали по 300 г картофеля. Сколько килограммов картофеля собрали с этого огорода, если с каждого квадратного метра собирали в 6 раз больше, чем сажали?
Ответ:
1) 300 ∙ 500 = 150000 (г) = 150 (кг) – масса высаженного картофеля. 2) 150 ∙ 6 = 900 (кг) – масса собранного картофеля.
1) 300 ∙ 6 = 1800 (г) – картофеля собрали с 1 м². 2) 1800 ∙ 500 = 900000 (г) = 900 (кг) – масса собранного картофеля.
Ответ: масса собранного картофеля составляет 900 кг.
Повтори единицы массы — грамм и килограмм, а также единицы площади.
Оформляем условие в виде таблицы.
Рассуждаем.
Узнаем массу высаженного картофеля.
300 ∙ 500 = 150000 (г) = 150 (кг) — масса высаженного картофеля.
Продолжаем рассуждение.
Узнаем массу собранного картофеля.
150 ∙ 6 = 900 (кг) — картофеля собрали.
Записываем ответ.
Ответ: 900 кг картофеля собрали с огорода.
Номер 7.
Узнай площадь прямоугольного участка, если одна седьмая его часть составляет 28 м².
Ответ:
Площадь седьмой части – 28 м²
Площадь участка – ? м²
28 ∙ 7 = 196 (м²) – площадь прямоугольника.
Ответ: площадь прямоугольника составляет 196 м².
Повтори единицы площади, а также что такое доли.
Оформляем условие в виде краткой записи.
Площадь седьмой части — 28 м²
Площадь участка — ? м²
Рассуждаем.
Вычислим, чему равна площадь прямоугольника.
28 ∙ 7 = 196 (м²) — площадь прямоугольника.
Записываем ответ.
Ответ: 196 м² площадь прямоугольника.
Номер 8.
С каждых 100 м² опытного участка было собрано по 46 кг зерна нового сорта пшеницы. Сколько центнеров зерна при такой урожайности можно было бы получиться с 10000 м²?
Ответ:
100 м² – 46 кг
10000 м² – ? кг
1) 10000 : 100 = 100 (раз) – во столько раз пшеницы может быть собрано на возможном участке.
Во сколько раз больше участок, во столько раз больше и будет урожай пшеницы.
2) 100 ∙ 46 = 4600 (кг) = 4 т 6 ц – зерна можно было бы получить при такой же урожайности с участка площадью 10000 м².
Ответ: 4 т 6 ц зерна получается с участка площадью 10000 м2.
Повтори единицы массы — килограмм и центнер, а также единицы площади.
Оформляем условие в виде краткой записи.
100 м² — 46 кг
10000 м² — ? кг
Рассуждаем.
Узнаем, во столько раз больше возможный участок, чем опытный участок.
10000 : 100 = 100 (раз) — во столько больше.
Продолжаем рассуждение.
Во сколько раз больше участок, во столько раз больше и будет урожай пшеницы.
100 ∙ 46 = 4600 (кг) = 46 (ц) — зерна можно было бы получить.
Записываем ответ.
Ответ: 46 ц зерна можно было бы получить при такой же урожайности.
Задание на полях страницы
Ребус.
Перед нами ребус, для того чтобы найти недостающие цифры необходимо выполнить умножение.
Рассмотрим ребус.
Рассуждаем.
Умножаем на единицы. На какое число надо умножить 3, чтобы получилось 9? Это число 3. 3 ∙ 3 = 9
4 ∙ 3 = 12. Пишу 2 под десятками, а 1 сот. запомню и прибавлю к сотням после умножения сотен.
После того, как к сотням прибавили 1 сот., которая получилась при умножении десятков, под сотнями записали 7. 7 – 1 = 6.
Какое число надо умножить на 3, чтобы получилось 6? Это число 2.
Какое число надо умножить на 3, чтобы получилось двузначное число с 5 единицами? Это число 5. 5 ∙ 3 = 15
Умножаем на десятки. На какое число надо умножить 3, чтобы получилось 2 в конце числа? Это число 4. 3 ∙ 4 = 12.
Умножаем десятки. 4 ∙ 4 = 16. 16 + 1 = 17
Умножаем сотни. 2 ∙ 4 = 8. 8 + 1 = 9
5 ∙ 4 = 20
Складываем неполные произведения: 215449.
Оформим задание в тетрадь.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽
Напишите свой комментарий.