Математика 4 класс учебник Моро, Бантова 1 часть ответы – страница 78

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Задание вверху страницы.
Вспомни правила умножения с числами 0 и 1. Вычисли:
Ответ:
1 ∙ 8 = 8 312 ∙ 1 = 312 0 ∙ 35 = 0
1 ∙ 1 = 1 703 ∙ 1 = 703 0 ∙ 100 = 0
918 ∙ 0 = 0 10 ∙ 1 = 10
617 ∙ 0 = 0 10 ∙ 0 = 0
Разные арифметические действия основывают на разных свойствах и правилах, но есть и общие, характерные для всех арифметических действий.
Например, переместительное свойство, сочетательное свойство – они характерны для разных арифметических действий.
А такие свойства, как:
Правило прибавления числа к нулю, 0 + а;
Правило прибавления нуля к числу, а + 0;
Правило умножения числа на 1, а ∙ 1;
Правило умножения числа на 0, а ∙ 0;
Правило деления числа на 1, а : 1;
Правило деления 0 на число, 0 : а, являются специфичными.
Выполняем вычисления.
1 ∙ 8 = 8 312 ∙ 1 = 312 0 ∙ 35 = 0
1 ∙ 1 = 1 703 ∙ 1 = 703 0 ∙ 100 = 0
918 ∙ 0 = 0 10 ∙ 1 = 10
617 ∙ 0 = 0 10 ∙ 0 = 0
Оформляем задание в тетрадь.
Номер 340.
Ответ:
0 дес. ∙ 5 + 3 дес. = 3 дес.
0 тыс. ∙ 7 + 4 дес. = 4 дес.
0 сот. ∙ 3 + 2 сот. = 2 сот.
0 сот. ∙ 1 + 1 сот. = 1 сот.
Разные арифметические действия основывают на разных свойствах и правилах, но есть и общие, характерные для всех арифметических действий.
Например, переместительное свойство, сочетательное свойство – они характерны для разных арифметических действий.
А такие свойства, как:
Правило прибавления числа к нулю, 0 + а;
Правило прибавления нуля к числу, а + 0;
Правило умножения числа на 1, а ∙ 1;
Правило умножения числа на 0, а ∙ 0;
Правило деления числа на 1, а : 1;
Правило деления 0 на число, 0 : а, являются специфичными.
Выполняем вычисления устно.
0 дес. ∙ 5 + 3 дес. = 3 дес.
0 тыс. ∙ 7 + 4 дес. = 4 дес.
0 сот. ∙ 3 + 2 сот. = 2 сот.
0 сот. ∙ 1 + 1 сот. = 1 сот.
Оформляем задание в тетрадь при необходимости.
Номер 341.
Ответ:
803 ∙ 5 = 4015
4019 ∙ 7 = 28133
50801 ∙ 4 = 203204
90048 ∙ 7 = 630336
41008 ∙ 6 = 246048
70032 ∙ 8 = 560256
Решение столбиком:

Помни о том, что существует алгоритм объяснения умножения многозначного числа на однозначное. Следуй ему и помни, что записывать многозначные числа нужно предельно внимательно, не пропуская разрядов.
1) Записываю первый множитель так, чтобы каждая цифра стояла в своей клетке. Ставлю знак умножить.
2) Записываю второй множитель так, чтобы разряд стоял под разрядом.
3) Провожу черту, обозначающую знак равно.
4) Умножение начинаю с единиц низшего разряда.
5) Умножаю десятки (аналогично умножаю все разряды).
6) Умножение окончено. Читаю ответ.
Выполняем вычисления.

Оформляем задание в тетрадь.
803 ∙ 5 = 4015
4019 ∙ 7 = 28133
50801 ∙ 4 = 203204
90048 ∙ 7 = 630336
41008 ∙ 6 = 246048
70032 ∙ 8 = 560256
Номер 342.
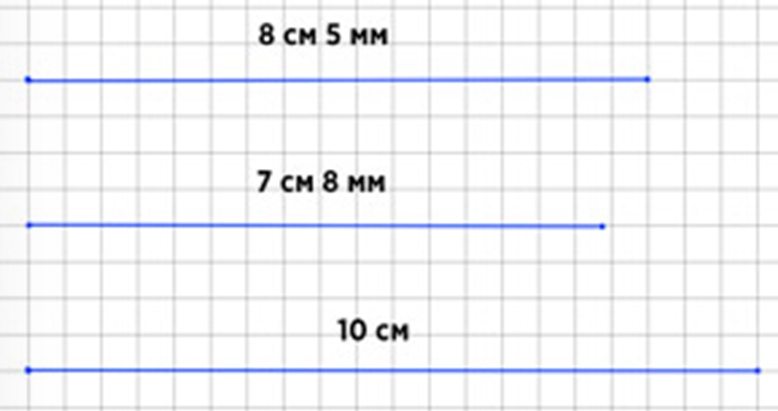
Начерти три отрезка. Длина первого 8 см 5 мм, что на 7 мм больше длины второго и на 1 см 5 мм меньше длины третьего отрезка.
Ответ:8 см 5 мм − 7 мм = 7 см 8 мм – длина второго отрезка. 8 см 5 мм + 1 см 5 мм = 10 см – длина третьего отрезка. 8 см 5 мм – длина первого отрезка.

Будь внимателен! Существуют два вида задач в зависимости от формулировки условия: в прямой и косвенной форме.
Задачи очень похожи по формулировкам, но их суть и соответственно решения будут отличаться. Отношение в прямой форме, т.е. зависимость очевидна: это больше, чем это. Условно задача в косвенной форме формулируется так: это на столько-то больше, чем то.
Решаются эти задачи из-за этого по-разному. Задача в прямой форме решается вычитанием, если условие: «на х меньше», сложением: «на х больше».
Задача в косвенной форме решается тоже в зависимости от вопроса: «это на х больше», значит, решается вычитанием, а если: «это на х меньше», значит, решается сложением.
Оформляем условие в виде краткой записи.
1 отрезок – 8 см 5 мм
2 отрезок – ?, на 7 мм > и на 1 см 5 мм <
3 отрезок – ?
Рассуждаем.
Чтобы узнать, чему равна длина второго отрезка, нужно из длины первого вычесть 7 мм.
8 см 5 мм − 7 мм = 7 см 8 мм – длина второго отрезка.
Продолжаем рассуждение.
Чтобы узнать, чему равна длина третьего отрезка, нужно к длине первого прибавить 1 см 5 мм.
8 см 5 мм + 1 см 5 мм = 10 см – длина третьего отрезка.
Оформляем задание в тетрадь.
Чертим 3 отрезка длинами 8 см 5 мм, 7 см 8 мм и 10 см.
Номер 343.
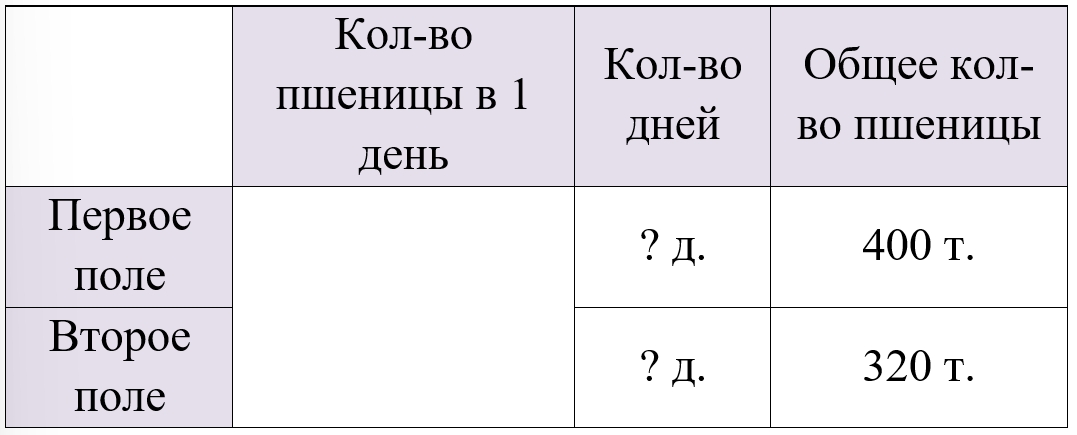
Комбайнер убирал 9 дней пшеницу на двух полях. На первом поле он собрал 400 т пшеницы, а на втором – 320 т. Сколько тонн зерна убирал комбайнер за 1 день, если ежедневная выработка была одинаковой?
Ответ:
1) 400 + 320 = 720 (т) – пшеницы убрали за 9 дней.
2) 720 : 9 = 80 (т)
Ответ: 80 тонн пшеницы убирают за 1 день всего.
Помни о том, каков конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а ∙ 3, а – первый множитель, а 3 – количество множителей.
Помни о зависимости между компонентами и результатом действия умножения:
1 множитель ∙ 2 множитель = значение произведения.
Значение произведения : 1 множитель = 2 множитель.
Значение произведения : 2 множитель = 1 множитель.
Данная задача: вида «количество пшеницы в 1 день, количество дней, общее количество пшеницы» характеризуется зависимостями между компонентами:
Количество пшеницы в 1 день ∙ кол-во дней = общее кол-во пшеницы.
Общее кол-во пшеницы : количество пшеницы в 1 день = кол-во дней.
Общее кол-во пшеницы : кол-во дней = количество пшеницы в 1 день.
Оформляем условие в виде таблицы.
Рассуждаем.
Чтобы узнать, сколько пшеницы было собрано с обоих полей, складываю количество пшеницы каждого поля.
1) 400 + 320 = 720 (т) – пшеницы убрали за 9 дней.
Продолжаем рассуждение.
Чтобы узнать, сколько пшеницы было собрано за 1 день, нужно общее количество пшеницы разделить на количество дней.
2) 720 : 9 = 80 (т)
Записываем ответ.
Ответ: 80 тонн пшеницы убирают за 1 день.
Решение выражением:
(400 + 320) : 9, где 400 + 320 – общее количество собранной пшеницы с обоих полей за 9 дней
Номер 344.
На мельницу отправили пшеницу на 10 машинах, по 42 ц на каждой, а ячменя в 3 раза меньше, чем пшеницы. На сколько центнеров больше отправили пшеницы, чем ячменя?
Ответ:
1) 42 ∙ 10 = 420 (ц) – отправили пшеницы.
2) 420 : 3 = 140 (ц) – отправили ячменя.
3) 420 − 140 = 280 (ц) – пшеницы больше
Ответ: на 280 ц больше отправили пшеницы.
Помни о том, каков конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а ∙ 3, а – первый множитель, а 3 – количество множителей.
Помни о зависимости между компонентами и результатом действия умножения:
1 множитель ∙ 2 множитель = значение произведения.
Значение произведения : 1 множитель = 2 множитель.
Значение произведения : 2 множитель = 1 множитель.
Данная задача: вида «кол-во пшеницы в 1 машине, количество машин, общее количество пшеницы» характеризуется зависимостями между компонентами:
Кол-во пшеницы 1 машины ∙ кол-во машин = общее кол-во пшеницы.
Общее кол-во пшеницы : кол-во машин = кол-во пшеницы 1 машин.
Общее кол-во пшеницы : кол-во пшеницы 1 машины = кол-во машин.
Оформляем условие в виде краткой записи.

Рассуждаем.
Чтобы узнать, сколько пшеницы отправили на мельницу, нужно количество центнеров в одной машине умножить на количество машин.
1) 42 ∙ 10 = 420 (ц) – отправили пшеницы.
Продолжаем рассуждение.
Чтобы узнать, сколько ячменя отправили на мельницу, нужно количество центнеров пшеницы разделить на 3, потому что известно, что ячменя в 3 раза меньше.
2) 420 : 3 = 140 (ц) – отправили ячменя.
Продолжаем рассуждение.
Чтобы узнать, на сколько больше было привезено пшеницы, чем ячменя, нужно из количества пшеницы вычесть количество ячменя.
3) 420 − 140 = 280 (ц)
Записываем ответ.
Ответ: на 280 ц больше отправили пшеницы.
Решение выражением: 420 – (42 ∙ 10 : 3)
Номер 345.
Запиши выражения и вычисли их значения.
1) Произведение чисел 8 и 3125 уменьшить на 5186. 2) Наименьшее шестизначное число увеличить в 10 раз, а результат уменьшить в 1000 раз. 3) Частное чисел 872 и 8 увеличить в 7 раз.
Ответ:1)

2)
100 000 · 10 : 1000 = 1000
3)

1) Произведение – умножение – множители
Уменьшить на – вычесть – вычитание – знак минус
2) а ∙ 10, увеличить в 10 раз, умножить на 10, добавить к записи числа один ноль
а : 1 000, уменьшить в 1 000 раз, разделить на 1 000, убрать в записи числа три нуля
3) частное – деление
увеличить в 7 раз – умножить
Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий. Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
Выполняем вычисления.
8 ∙ 3 125 - 5 186 = 19 814

100 000 ∙ 10 : 1 000 = 1 000
1) 100 000 ∙ 10 = 1 000 000
2) 1 000 000 : 1 000 = 1 000
872 : 8 ∙ 7 = 763
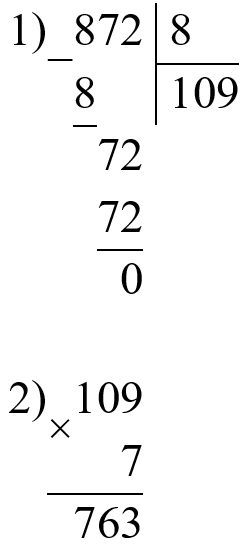
Выполняем проверку.
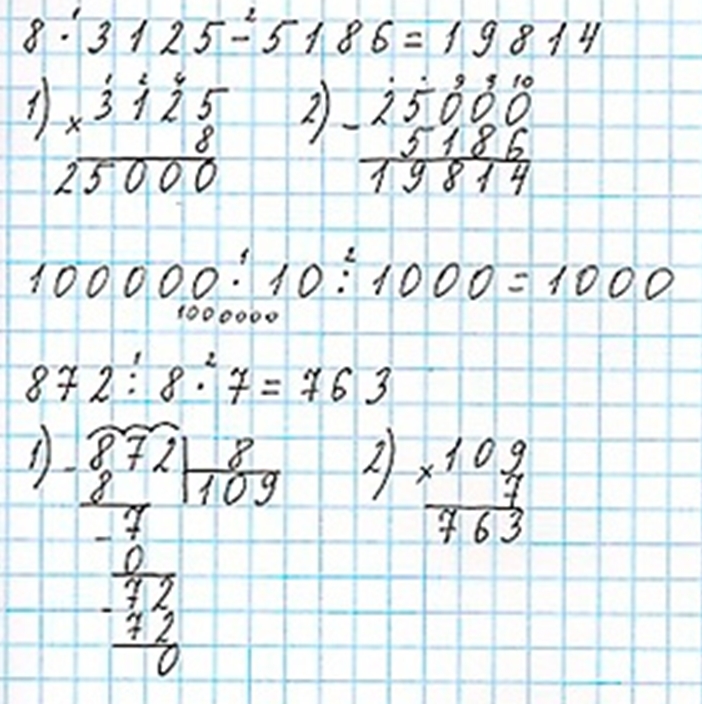
Номер 346.
Рассмотри рисунки и объясни, чем похожи и чем различаются рисунки: 1 и 2, 2 и 3, 3 и 4, 1 и 4.

Рисунки похожи тем, что у них есть два круга (красный и синий) и есть центр окружность. Рисунки отличаются тем, что: 1 – окружности находятся рядом; 2 – окруж. касаются друг друга; 3 – окруж. пересекаются; 4 – одна окружность находится в центре другой окружности.
Для того, чтобы объяснить схожести и различия рисунков, опишем каждый рисунок по всем возможным признакам: цвет, размер, количество, взаимное расположение и т.д.
Рассмотри рисунки на полях страницы.
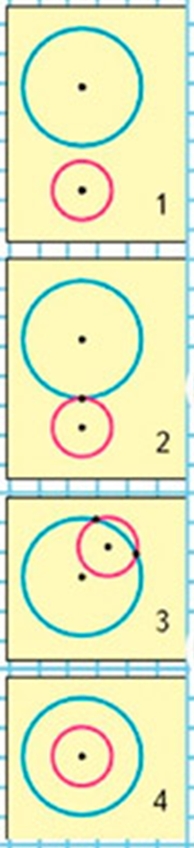
Определим, чем они похожи.
Рисунки похожи тем, что у них есть два круга (красный и синий) и есть центр окружность.
Определим, чем они отличаются.
Рисунки отличаются тем, что:
1 – окружности находятся рядом;
2 – окружности касаются друг друга;
3 – окружности пересекаются;
4 – одна окружность находится в центре другой окружности.
Номер 347.
Сколько в числе 15400 десятков? сотен? тысяч? Сколько единиц в числе, содержащем 208 дес.? 32 сот.?
Ответ:15400 – 1540 д., 154 сот., 15 тыс. 208 дес. – 2080 ед. 32 сот. – 3200 ед.
Помни о том, что одна и та же цифра, стоя на разных позициях в записи числа может обозначать количество единиц разных разрядов.
Помни о том, в каком порядке следуют разряды:
единицы,
десятки,
тысячи,
единицы тысяч,
десятки тысяч,
сотни тысяч.
При необходимости обращайтесь к таблице, чтобы вспомнить классово-разрядный состав числа.
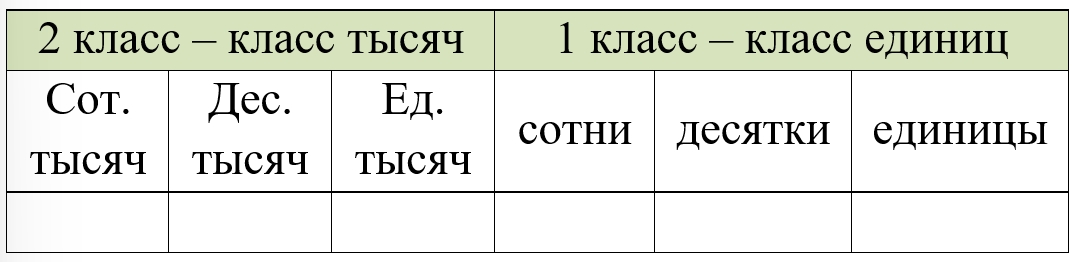
Запишем все числа, чтобы понять, сколько в них единиц какого разряда.
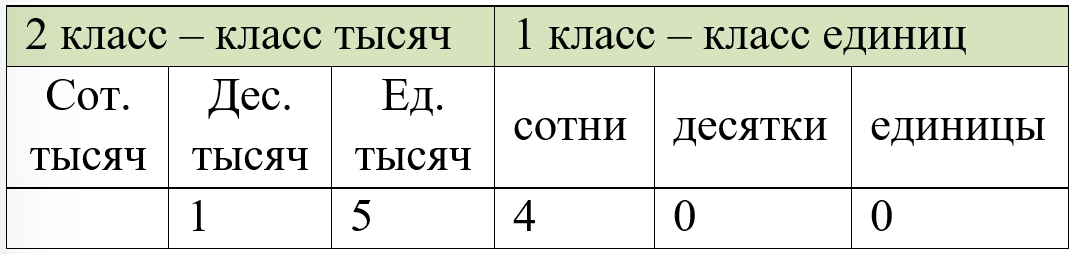
В числе 15 400: 0 десятков, 4 сотни, 5 тысяч или если смотреть на общее количество разрядов: 1 540 десятков, 154 сотни, 15 тысяч.
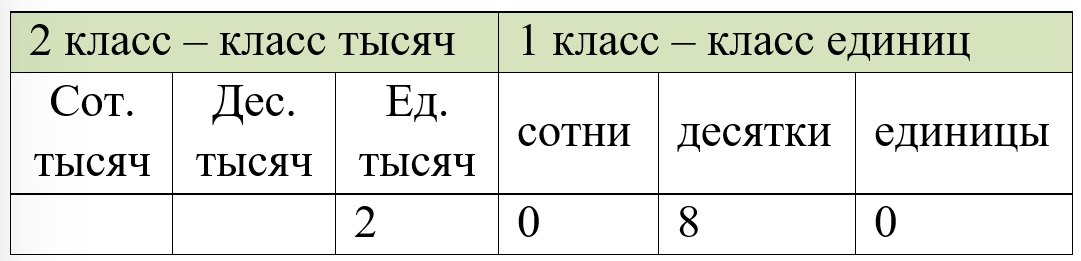
Число, в котором 208 десятков – 2 080 ед., значит в этом числе 2080 единиц.
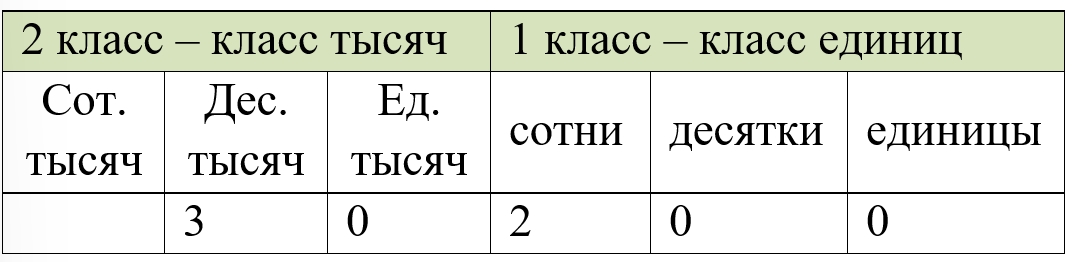
Число, в котором 32 сотни – это число 3 200 ед., значит, в этом числе 3 200 единиц.
Оформим задание в тетрадь.
15400 – 1540 д., 154 сот., 15 тыс.
208 дес. – 2080 ед.
32 сот. – 3200 ед.
Номер 348.
Ответ:
Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий. Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Помни о том, что существует алгоритм письменного деления. Следуй ему, объясняя, как выполняешь деление:
1) Выделю первое неполное делимое, чтобы определить количество цифр в частном;
2) Нахожу цифру сотен в частном;
3) Нахожу, сколько сотен разделили;
4) Нахожу, сколько сотен осталось разделить;
5) Образую второе неполное делимое;
6) Нахожу, количество десятков в частном;
7) Нахожу, сколько десятков разделили;
8) Нахожу, сколько десятков осталось разделить;
9) Образую третье неполное делимое;
10) Нахожу количество единиц в частном;
11) Нахожу, сколько единиц разделили;
12) Нахожу, сколько единиц осталось разделить;
13) Читаю ответ
Помни о том, что существует алгоритм объяснения умножения трехзначного числа на однозначное. Следуй ему:
1) Записываю первый множитель так, чтобы каждая цифра стояла в своей клетке. Ставлю знак умножить;
2) Записываю второй множитель так, чтобы разряд стоял под разрядом;
3) Провожу черту, обозначающую знак равно;
4) Умножение начинаю с единиц низшего разряда;
5) Умножаю десятки;
6) Умножаю сотни;
7) Умножение окончено. Читаю ответ.
Следуй плану при устном объяснении вычитания в столбик:
1) Записываю уменьшаемое так, чтобы каждая цифра стояла в своей клетке. Ставлю знак минус;
2) Записываю вычитаемое так, чтобы разряд стоял под разрядом;
3) Провожу черту, обозначающую знак равно;
4) Вычитание начинаю с единиц низшего разряда. Вычитаю единицы;
5) Вычитаю десятки;
6) Вычитаю сотни;
7) Вычитание окончено. Читаю ответ.
Выполняем вычисления по действиям.
45 010 − (3 908 + 17 613) = 23 489

60 000 − 2 407 + 5 849 = 63 442
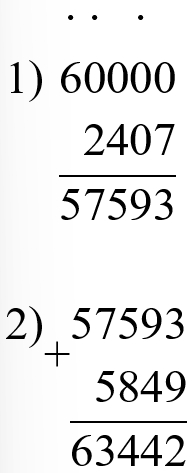
Выполняем умножение с устным пояснением.
Пишу: 91 005 ∙ 3.
Умножаю единицы: 5 ∙ 3 = 15. 15 ед. – это 1 дес. и 5 ед., 5 ед. пишу под единицами, а 1 дес. запомню и прибавлю к десяткам после умножения десятков.
Умножаю десятки: 0 ∙ 3 = 0. К 0 дес. прибавляю 1 дес., который получен при умножении единиц: 0 + 1 = 1. Пишу 1 под десятками.
Умножаю сотни: 0 ∙ 3 = 0. Пишу 0 под сотнями.
Умножаю единицы тысяч: 1 ∙ 3 = 3. Пишу 3 под единицами тысяч.
Умножаю десятки тысяч: 9 ∙ 3 = 27. 27 ед. тыс. – это 2 сот. тыс. и 7 дес. тыс.; 7 дес. тыс. пишу под десятками тысяч, а 2 сот. тыс. запишу под сотнями тысяч, так как других сотен тысяч для умножения нет.
Читаю ответ: 273 015.
Далее рассуждаю аналогично.
Выполняем вычисления и оформляем задание в тетрадь.

Номер 349.
Переставляя карточки с цифрами сделай равенство верным.

63 : 21 = 3
Переставляй карточки, пока не получишь верное равенство. Можешь сделать карточки с цифрами и знаками и переставлять их, пока не найдешь верно решение.
Выполняем вычисления.
63 : 21 = 3, потому что 21 ∙ 3 = 63, это по 21 – 3 раза, где 21 – одинаковое слагаемое, а 3 – количество одинаковых слагаемых
Оформляем задание в тетрадь.
63 : 21 = 3
Задание внизу страницы
Вычисли.
Ответ:
Помни о том, что существует алгоритм объяснения умножения многозначного числа на однозначное. Следуй ему и будь предельно внимателен при записи многозначного числа – не пропускай разрядов.
1) Записываю первый множитель так, чтобы каждая цифра стояла в своей клетке. Ставлю знак умножить.
2) Записываю второй множитель так, чтобы разряд стоял под разрядом.
3) Провожу черту, обозначающую знак равно.
4) Умножение начинаю с единиц низшего разряда.
5) Умножаю десятки.
6) Умножаю сотни.
7) Умножение окончено. Читаю ответ.
Составляем алгоритм.
609 ∙ 7 (аналогично 32 0009 ∙ 3)
1) Записываю первый множитель так, чтобы каждая цифра стояла в своей клетке. Ставлю знак умножить.
2) Записываю второй множитель так, чтобы разряд стоял под разрядом.
3) Провожу черту, обозначающую знак равно.
4) Умножение начинаю с единиц низшего разряда; 9 ед. ∙ 7 = 63 ед. – это 6 дес. 3 ед., значит, 3 единиц записываю в разряд единиц, а 6 десятков запоминаю.
5) Умножаю десятки; 0 де. ∙ 7 = 0 дес., да еще 6 дес. – 6 дес.
6) Умножаю сотни; 6 сот. ∙ 7 = 42 сот., это 3 тыс. 2 сот., значит, 2 сот. записываю в разряд сотен, а 4 тыс. записываю в разряд единиц тысяч.
7) Умножение окончено. Читаю ответ. Значение произведения от умножения 609 на 7 равно 4 263.
Выполняем вычисления.
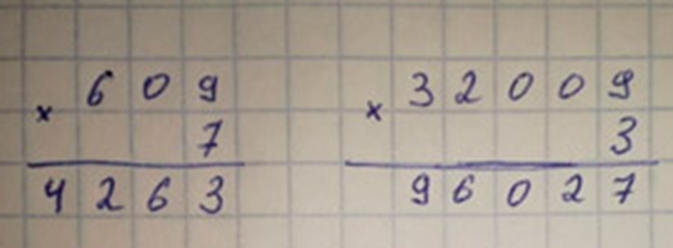
Оформляем задание в тетрадь.
Задание на полях страницы
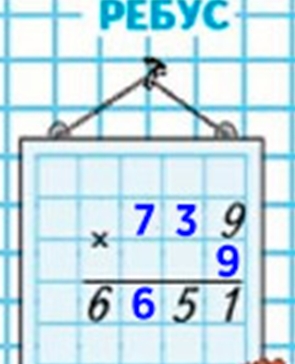
Ребус.


Вспомни названия компонентов действия умножения и зависимость между компонентами и результатом действия умножения:
1 множитель ∙ 2 множитель = значение произведения.
Значение произведения : 1 множитель = 2 множитель.
Значение произведения : 2 множитель = 1 множитель.
Рассуждаем и выполняем вычисления.
Количество единиц первого множителя – 9, а значения произведения – 1. Значит, необходимо вспомнить, при умножении какого числа на 9 получается число с единицей на конце. Это число 9. Потому что 9 ∙ 9 = 81, значит, второй множитель равен 9.
Тогда, 9 ед. ∙ 9 = 81 ед. – это 1 ед., 8 дес, значит 8 дес. запоминаем.
Узнаем количество десятков первого множителя: х ∙ 9 + 8 = число у которого 5 в кол-ве единиц.
Тогда, получается, что х ∙ 9 = число с 7 на конце.
Это число 27, потому что 3 ∙ 9 = 27.
Значит, количество десятков в первом множителе – 3 дес.
Тогда, 3 дес. ∙ 9 = 27 дес. - это 2 сот. 7 дес. тогда 2 сот запоминаем.
Узнаем количество сотен: х ∙ 9 + 2 = число, в котором 6 дес. Это может быть число 7, потому что 7 сот. ∙ 9 = 63 сот. + 2 сот. - 65 сот. , значит, в значении произведения 6 сотен.
Получаем равенство: 739 ∙ 9 = 6 651
Оформляем задание в тетрадь.
Вспомни правила умножения с числами 0 и 1. Вычисли:
Ответ:
1 ∙ 8 = 8 312 ∙ 1 = 312 0 ∙ 35 = 0
1 ∙ 1 = 1 703 ∙ 1 = 703 0 ∙ 100 = 0
918 ∙ 0 = 0 10 ∙ 1 = 10
617 ∙ 0 = 0 10 ∙ 0 = 0
Номер 344.
Ответ:
0 дес. ∙ 5 + 3 дес. = 3 дес.
0 тыс. ∙ 7 + 4 дес. = 4 дес.
0 сот. ∙ 3 + 2 сот. = 2 сот.
0 сот. ∙ 1 + 1 сот. = 1 сот.
Номер 345.
Ответ:
803 ∙ 5 = 4015
4019 ∙ 7 = 28133
50801 ∙ 4 = 203204
90048 ∙ 7 = 630336
41008 ∙ 6 = 246048
70032 ∙ 8 = 560256
Решение столбиком:

Номер 346.
Начерти три отрезка. Длина первого 8 см 5 мм, что на 7 мм больше длины второго и на 1 см 5 мм меньше длины третьего отрезка.
Ответ:8 см 5 мм − 7 мм = 7 см 8 мм – длина второго отрезка. 8 см 5 мм + 1 см 5 мм = 10 см – длина третьего отрезка. 8 см 5 мм – длина первого отрезка.

Номер 347.
Комбайнер убирал 9 дней пшеницу на двух полях. На первом поле он собрал 400 т пшеницы, а на втором — 320 т. Сколько тонн зерна убирал комбайнер за 1 день, если ежедневная выработка была одинаковой?
Ответ:
1) 400 + 320 = 720 (т) – пшеницы убрали за 9 дней.
2) 720 : 9 = 80 (т) – пшеницы за день
Ответ: 80 тонн пшеницы убирают за 1 день.
Номер 348.
На мельницу отправили пшеницу на 10 машинах, по 42 ц на каждой, а ячменя в 3 раза меньше, чем пшеницы. На сколько центнеров больше отправили пшеницы, чем ячменя?
Ответ:
1) 42 ∙ 10 = 420 (ц) – отправили пшеницы. 2) 420 : 3 = 140 (ц) – отправили ячменя. 3) 420 − 140 = 280 (ц) – пшеницы больше Ответ: на 280 ц больше отправили пшеницы.
Номер 349.
Запиши выражения и вычисли их значения.
1) Произведение чисел 8 и 3125 уменьшить на 5186. 2) Наименьшее шестизначное число увеличить в 10 раз, а результат уменьшить в 1000 раз. 3) Частное чисел 872 и 8 увеличить в 7 раз.
Ответ:1)

2)
100 000 · 10 : 1000 = 1000
3)

Номер 350.
Рассмотри рисунки и объясни, чем похожи и чем различаются рисунки: 1 и 2, 2 и 3, 3 и 4, 1 и 4.

Рисунки похожи тем, что у них есть два круга (красный и синий) и есть центр окружность. Рисунки отличаются тем, что: 1 – окружности находятся рядом; 2 – окруж. касаются друг друга; 3 – окруж. пересекаются; 4 – одна окружность находится в центре другой окружности.
Номер 351.
Сколько в числе 15400 десятков? сотен? тысяч? Сколько единиц в числе, содержащем 208 дес.? 32 сот.?
Ответ:15400 – 1540 д., 154 сот., 15 тыс. 208 дес. – 2080 ед. 32 сот. – 3200 ед.
Номер 352.
Ответ:
Номер 353.
Как сделать равенство верным, не заменяя карточки с цифрами на другие?

63 : 21 = 3
Задание внизу страницы
Вычисли.
Ответ:
Задание на полях страницы
Ребус.


С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.