Математика 4 класс учебник Моро, Бантова 1 часть ответы – страница 66

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 306.
Масса тыквы, арбуза и дыни вместе 16 кг, масса тыквы и арбуза 13 кг, масса арбуза и дыни 8 кг. Найди массу дыни, арбуза и тыквы в отдельности.

1-й способ решения:
1) 16 – 8 = 8 (кг) – тыква.
2) 16 – 13 = 3 (кг) – дыня.
3) 8 – 3 = 5 (кг) – арбуз.
Ответ: 8 кг весит тыква, 3 кг весит дыня, 5 кг весит арбуз.
2-й способ решения:
1) 16 – 13 = 3 (кг) – дыня
2) 8 – 3 = 5 (кг) – арбуз
3) 13 – 5 = 8 (кг) – тыква
Ответ: 8 кг, 3 кг, 5 кг.
Для того, чтобы решить задачу, обращайтесь к рисунку, составленному к задаче. По нему легко увидеть решение. Попытайтесь выразить значение массы любого овоща, потому что найти массы других овощей потом будет легко.
Рассуждайте так: «если арбуз и дыня вместе весят 8 кг, а все три овоща – 16 кг, то получается, что на тыкву приходится ...»
Рассмотрим схематический чертеж к заданию.

1) 16 – 8 = 8 (кг) – весит тыква.
2) 16 – 13 = 3 (кг) – дыня.
3) 8 – 3 = 5 (кг) – арбуз.
Ответ: 8 кг, 3 кг, 5 кг.
Рассуждаем.
Если арбуз и дыня вместе весят 8 кг, а все три овоща – 16 кг, то получается, что на тыкву приходится оставшаяся часть массы, потому что общая масса трех овощей складывается из массы тыквы, арбуза и дыни. Значит, чтобы узнать, сколько весит тыква, нужно из общей массы овощей вычесть массу дыни и арбуза.
1) 16 – 8 = 8 (кг) – весит тыква.
Продолжаем рассуждение.
Мы узнали, что масса тыквы – 8 кг. А общая масса тыквы и арбуза – 13 кг. При этом общая масса тыквы и дыни, складывается из массы обоих предметов. Значит, чтобы узнать, сколько весит арбуз, нужно из общей массы вычесть массу тыквы.
2) 13 кг – 8 кг = 5 (кг) – весит арбуз.
Продолжаем рассуждение.
Общая масса арбуза и дыни равна 8 кг. Арбуз весит 5 кг. Значит, чтобы узнать, сколько весит один предмет, нужно из общей массы вычесть массу другого предмета.
3) 8 кг – 5 кг = 3 (кг) – масса дыни.
Проверка.
Проверка: общая масса всех предметов – 16 кг.
8 кг + 5 кг + 3 кг = 16 кг – верно.
Записываем ответ.
Ответ: тыква – 8 кг, арбуз – 5 кг, дыня – 3 кг.
Номер 307.
В трёх школах 1945 учеников. В первой и второй школах вместе 1225 учеников, а во второй и третьей — 1300 учеников. Сколько учеников в каждой школе? Реши и проверь решение.
Ответ:1-й способ решения:

1) 1945 – 1225 = 720 (уч.) – в 3-ей школе.
2) 1945 – 1300 = 645 (уч.) – в 1-ой школе.
3) 1300 – 720 = 580 (уч.) – во 2-ой школе.
Ответ: 720 учеников в третьей школе., 645 учеников в первой школе., 580 учеников во второй школе.
1) 720 + 645 + 580 = 1945 (уч.)
Проверка: 720 + 645 + 580 = 1945 (уч.)
2-й способ решения:
1) 1 945 – 1 300 = 645 (уч.) – в 1 школе
2) 1 225 – 645 = 580 (уч.) – во 2 школе
3) 1 300 – 580 = 720 (уч.) – в 3 школе
Ответ: 645 уч., 580 уч., 720 уч.
Данная задача аналогична задаче 306. Значит, для решения также необходимо составить схематический рисунок или краткую запись.
По эти моделям будет легко увидеть решение. Попытайтесь выразить количество человек любой школы, потому что вычислить количество человек в оставшихся школах будет легко.
Оформляем условие в виде схематического чертежа.

Рассуждаем.
В первой и второй школе вместе 1 225 учеников, а всего учеников – 1 945. И общее количество учащихся складывается из количества учеников каждой из трех школ. Значит, чтобы узнать, сколько учеников в третьей школе, из общего количества учеников вычитаем количество учеников первой и второй школы.
1) 1945 – 1225 = 720 (уч.) – в 3-ей школе.
Продолжаем рассуждение.
Во второй и третьей школе вместе 1 300 учеников, а всего учеников в трех школах – 1945. Мы знаем, что общее количество учеников в школах складывается из количества учеников каждой школы. Значит, чтобы узнать, сколько учеников в первой школе, нужно из общего количества учеников вычесть количество учеников второй и третьей школы.
2) 1945 – 1300 = 645 (уч.) – в 1-ой школе.
Продолжаем рассуждение.
В третьей и второй школах вместе 1 300 учеников, а в третьей – 720 уч. Значит, чтобы узнать, сколько учеников во второй школе, нужно из общего количества вычесть количество учеников третьей школы.
3) 1300 – 720 = 580 (уч.) – во 2-ой школе.
Проверка.
720 + 645 + 580 = 1945 (уч.).
Записываем ответ.
Ответ: 720 уч., 645 уч., 580 уч.
Номер 308.
Расставь скобки, чтобы равенства стали верными.
Ответ:
Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий. Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
а · 10, значит, увеличить в 10 раз, т.е. умножить, значит, добавить к записи числа один ноль.
Вычисление значений выражения сводится к применению правил:
Правило прибавления суммы к числу:
а + (в + с) = (а + в) + с.
Правило вычитания суммы из числа:
а – (в + с) = (а – в) – с.
Правило вычитания числа из суммы:
(а + в) – с = (а – с) + в.
Выполняем вычисления.
(640 – 480) : 4 + 360 = 400
1) 640 – 480 = 640 – (440 + 40) = (640 – 440) – 40 = 200 – 40 = 160, по правилу вычитания суммы из числа.
2) 160 : 4 = 16 дес. : 4 = 4 дес. = 40
3) 40 + 360 = 40 + (300 + 60) = 300 + (40 + 60) = 300 + 100 = 400, по правилу прибавления суммы к числу.
120 + 120 : (4 + 6) = 132
1) 4 + 6 = 10
2) 120 : 10 = 12, по правилу деления числа на 10.
3) 120 + 12 = 120 + (10 + 2) = (120 + 10) + 2 = 130 + 2 = 132, по правилу прибавления суммы к числу.
160 : (4 · 2) + 10 = 30
1) 4 · 2 = 8
2) 160 : 8 = 16 дес. : 8 = 2 дес. = 20
3) 20 + 10 = 30
(60 – 54 : 6) : 3 = 17
1) 54 : 6 = 9
2) 60 – 9 = (50 + 10) – 9 = 50 + (10 – 9) = 50 + 1 = 51, по правилу вычитания числа из суммы.
3) 51 : 3 = 17
Оформляем задание в тетрадь.

Номер 309.
Реши задачи, составив уравнения.
1) Разность неизвестного числа и числа 80 равна сумме чисел 360 и 140. Найди неизвестное число. 2) Из числа 430 вычли задуманное число и получили частное чисел 640 и 8. Какое число задумали?
Ответ:1)

2)

Уравнение – равенство с неизвестной, при подстановке числа в которую, получается верное равенство.
Вспомни названия компонентов действия умножения, и зависимость между компонентами и результатом действия умножения:
1 множитель · 2 множитель = значение произведения.
Значение произведения : 1 множитель = 2 множитель.
Значение произведения : 2 множитель = 1 множитель.
Уменьшаемое – вычитаемое = значение разности.
Уменьшаемое – значение разности = вычитаемое.
Значение разности + вычитаемое = уменьшаемое.
Делимое : делитель = значение разности.
Делимое : значение разности = делитель.
Значение разности · делитель = делимое.
Составляем первое уравнение и вычисляем его.
Записываем уравнение:
x – 80 = 360 + 140
Преобразуем правую часть уравнения, вычисляя ее:
x – 80 = 500
Данное уравнение основано на арифметическом действии вычитания, где х – неизвестное уменьшаемое. Чтобы найти неизвестное уменьшаемое, нужно к значению разности прибавить вычитаемое:
x = 500 + 80
x = 580
Выполняем проверку, через подстановку числа в неизвестную. Значения совпали, значит, уравнение решено верно.
580 – 80 = 360 + 140
500 = 500
Записываем ответ:
Ответ: х = 500.
Составляем второе уравнение и вычисляем его.
Записываем уравнение:
430 – x = 640 : 8
Преобразуем правую часть уравнения, вычисляя значение суммы:
430 – x = 80
Данное уравнение основано на арифметическом действии вычитания, где х – неизвестное вычитаемое. Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть значение разности:
x = 430 – 80
x = 350
Выполняем проверку, через подстановку числа в неизвестную. Значения совпали, значит, уравнение решено верно.
430 – 350 = 640 : 8
80 = 80
Записываем ответ:
Ответ: x = 350
Оформляем задание в тетрадь.

Номер 310.
Расстояние между двумя посёлками 96 км. Мотоциклист отправился из первого посёлка и проехал до остановки четвёртую часть пути. Сколько километров ему осталось проехать?

1-й способ решения:
1) 96 : 4 = 24 (км) – проехал мотоциклист.
2) 96 – 24 = 72 (км) – осталось.
Ответ: 72 км осталось проехать мотоциклисту.
2-й способ решения:
если одну четвертую часть пути мотоциклист проехал, то осталось ему проехать три части из четырех или три четвертых части пути. Это в 3 раза больше, чем проехал мотоциклист.
1) 4 – 1 = 3 (части) – осталось проехать
2) 96 : 4 = 24 (км) – проехал или одна четвертая часть пути
3) 24 ∙ 3 = (20 + 4) ∙ 3 = 60 + 12 = 72 (км) – осталось проехать
Ответ: 72 км.
Доля – одна часть из тех, на которые разделили целое. Например, если целое разделили на 4 части, то доля – это одна четвертая, т.е. одна часть из четырех.
Одна вторая – половина целого.
Одна третья – третья часть от целого.
Одна четвертая – четвертинка или четвертая часть от целого.
Одна пятая – пятая часть от целого и т.д.
Первое слово в названии долей указывает на количество долей, которые взяли, а второе – на сколько частей разделили целое.
Помни о зависимости между частью и целым:
часть + часть = целое.
целое – 1 часть = 2 часть.
целое – 2 часть = 1 часть.
Рассмотрим схематический чертеж в учебнике.

Рассуждаем.
Расстояние между двумя поселками равно 96 км. Мотоциклист проехал до остановки одну четвертую часть пути. Одна четвертая, т.е. одна из четырех. Значит, общую длину пути разделили на 4, а взяли только одну.
1) 96 : 4 = 24 (км) – проехал мотоциклист.
Продолжаем рассуждение.
Длина всего пути складывается из длины части до остановки и оставшейся. Значит, чтобы узнать, какую часть пути осталось проехать, нужно из длины всего пути вычесть длину пути до остановки.
2) 96 – 24 = 72 (км) – осталось.
Записываем ответ.
Ответ: 72 км.
Номер 311.
Ответ:2000 см2 = 20 дм2
3 ч 10 мин = 190 мин
45 ц = 4500 кг
23 т = 23000 кг
23 км = 23000 м
600 с = 10 мин
Длина – величина, характеризующая протяженность объекта на плоскости, выражается в таких единицах измерения, как миллиметр, сантиметр, дециметр, метр, километр.
Помни о соотношении числовых значений единиц измерения длины:
1 см = 10 мм.
1 дм = 10 см.
1 м = 100 см.
1 м = 10 дм.
1 км = 1000 м.
Площадь – величина, которая характеризует размер части плоскости, занятой фигурой. Измеряется в таких единицах измерения, как: мм2, см2, дм2, м2, км2 и др.
Помни о соотношении числовых значений единиц измерения площади:
1 см2 = 100 мм2.
1 дм2 = 100 см2.
1 м2 = 10 000 см2.
1 м2 = 100 дм2.
Время – величина, характеризующая продолжительность какого-либо события и отношения его к временной прямой: прошлому, настоящему или будущему. Измеряется в таких единицах измерения, как: 1 секунда, 1 минута, 1 час, 1 сутки, 1 неделя, 1 месяц, 1 год, 1 век.
Помни о соотношении числовых значений единиц измерения времени:
1 мин – 60 сек.
1 час – 60 мин.
1 сут – 24 час.
1 мес – 28, 29, 30 или 31 сут.
1 год – 12 мес.
1 год – 356 сут.
Масса – величина, которая характеризует вес предмета, то, сколько он весит. Масса может измеряться в таких единицах измерения, как грамм, килограмм, центнер, тонна.
Помни о соотношении числовых значений единиц измерения времени:
1 кг = 1000 г.
1 ц = 100 кг.
1 т = 1000 кг.
Выполняем вычисления.
2 000 см2; 1 дм2 – 100 см2, потому что 10 см · 10 см = 100 см, значит, 2 000 см2 : 100 см2 = 20 дм2.
3 ч 10 мин; 1 час – 60 мин, значит, 60 мин · 3 = 180 мин да еще 10 минут – 190 минут.
45 ц; 1 ц – 100 кг, значит, 100 кг · 45 = 4 500 кг.
23 т; 1 т – 1 000 кг, значит, 1 000 · 23 = 23 000 кг.
23 км; 1 км – 1 000 м, значит, 1 000 · 23 = 23 000 м.
600 с; 1 мин – 60 сек, значит, 600 сек : 60 = 10 мин.
Оформляем задание в тетрадь.
2000 см2 = 20 дм2.
3 ч 10 мин = 190 мин.
45 ц = 4500 кг.
23 т = 23000 кг.
23 км = 23000 м.
600 с = 10 мин.
Номер 312.
Ответ:
Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий. Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Помни о том, что существует алгоритм письменного деления. Следуй ему, объясняя, как выполняешь деление:
1) Выделю первое неполное делимое, чтобы определить количество цифр в частном.
2) Нахожу цифру сотен в частном:
3) Нахожу, сколько сотен разделили:
4) Нахожу, сколько сотен осталось разделить:
5) Образую второе неполное делимое:
6) Нахожу, количество десятков в частном:
7) Нахожу, сколько десятков разделили:
8) Нахожу, сколько десятков осталось разделить:
9) Образую третье неполное делимое:
10) Нахожу количество единиц в частном:
11) Нахожу, сколько единиц разделили:
12) Нахожу, сколько единиц осталось разделить:
13) Читаю ответ.
Помни о том, что существует алгоритм объяснения умножения трехзначного числа на однозначное. Следуй ему:
1) Записываю первый множитель так, чтобы каждая цифра стояла в своей клетке. Ставлю знак умножить;
2) Записываю второй множитель так, чтобы разряд стоял под разрядом;
3) Провожу черту, обозначающую знак равно;
4) Умножение начинаю с единиц низшего разряда;
5) Умножаю десятки;
6) Умножаю сотни;
7) Умножение окончено. Читаю ответ.
Следуй плану при устном объяснении вычитания в столбик:
1) Записываю уменьшаемое так, чтобы каждая цифра стояла в своей клетке. Ставлю знак минус;
2) Записываю вычитаемое так, чтобы разряд стоял под разрядом;
3) Провожу черту, обозначающую знак равно;
4) Вычитание начинаю с единиц низшего разряда. Вычитаю единицы;
5) Вычитаю десятки;
6) Вычитаю сотни;
7) Вычитание окончено. Читаю ответ.
Выполняем вычисления по действиям.
32 546 + 7 008 + 82 309 = 121 863
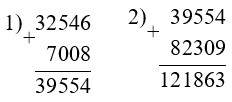
1 200 – 172 · 3 + 308 = 992
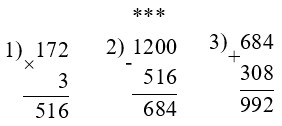
Оформляем задание в тетрадь.

Задание внизу страницы.
Ответ:
Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий. Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
Помни о том, что существует алгоритм письменного деления. Следуй ему, объясняя, как выполняешь деление:
1) Выделю первое неполное делимое, чтобы определить количество цифр в частном.
2) Нахожу цифру сотен в частном:
3) Нахожу, сколько сотен разделили:
4) Нахожу, сколько сотен осталось разделить:
5) Образую второе неполное делимое:
6) Нахожу, количество десятков в частном:
7) Нахожу, сколько десятков разделили:
8) Нахожу, сколько десятков осталось разделить:
9) Образую третье неполное делимое:
10) Нахожу количество единиц в частном:
11) Нахожу, сколько единиц разделили:
12) Нахожу, сколько единиц осталось разделить:
13) Читаю ответ.
Помни о том, что существует алгоритм объяснения умножения трехзначного числа на однозначное. Следуй ему:
1) Записываю первый множитель так, чтобы каждая цифра стояла в своей клетке. Ставлю знак умножить;
2) Записываю второй множитель так, чтобы разряд стоял под разрядом;
3) Провожу черту, обозначающую знак равно;
4) Умножение начинаю с единиц низшего разряда;
5) Умножаю десятки;
6) Умножаю сотни;
7) Умножение окончено. Читаю ответ.
Следуй плану при устном объяснении вычитания в столбик:
1) Записываю уменьшаемое так, чтобы каждая цифра стояла в своей клетке. Ставлю знак минус;
2) Записываю вычитаемое так, чтобы разряд стоял под разрядом;
3) Провожу черту, обозначающую знак равно;
4) Вычитание начинаю с единиц низшего разряда. Вычитаю единицы;
5) Вычитаю десятки;
6) Вычитаю сотни;
7) Вычитание окончено. Читаю ответ.
Выполняем вычисления по действиям.
20 782 + 5 203 + 63 870 = 89 855
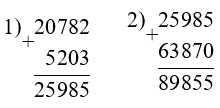
4 508 + 498 : 6 – 892 = 3 699
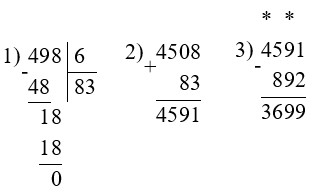
Оформляем задание в тетрадь.

Задание на полях страницы.
Магический квадрат.


Проверка: 130 + 120 + 170 = 300 + 120 = 420 180 + 140 + 100 = 320 + 100 = 420 110 + 160 + 150 = 110 + 310 = 420 130 + 180 + 110 = 310 + 110 = 420 120 + 140 + 160 = 120 + 300 = 420 170 + 100 + 150 = 320 + 100 = 420 130 + 140 + 150 = 270 + 150 = 420 110 + 140 + 170 = 250 + 170 = 420
Магический квадрат – квадрат, в котором все числа, стоящие на одной прямой по горизонтали, вертикали и диагонали в сумме образую одно и то же число.
Вычисление значений выражения сводится к применению правил:
Правило прибавления числа к сумме:
(а + в) + с = (а + с) + в.
Правило прибавления суммы к числу:
а + (в + с) = (а + в) + с.
Выполняем вычисления.
130 + 120 + 170 = 300 + 120 = 300 + (100 + 20) = (300 + 100) + 20 = 400 + 20 = 420, по правилу прибавления числа к сумме.
180 + 140 + 100 = 320 + 100 = (300 + 20) + 100 = (300 + 100) + 20 = 400 + 20 = 420, по правилу прибавления числа к сумме.
110 + 160 + 150 = 270 + 150 = 270 + (130 + 20) = (270 + 130) + 20 = 400 + 20 = 420, по правилу прибавления суммы к числу.
110 + 160 + 150 = 260 + 160 = 260 + (140 + 20) = (260 + 140) + 20 = 400 + 20 = 420, по правилу прибавления суммы к числу.
130 + 180 + 100 = 240 + 180 = (220 + 20) + 180 = (180 + 20) + 220 = 200 + 220 = 420, по правилу прибавления числа к сумме.
120 + 140 + 160 = 260 + 160 = 260 + (140 + 20) = (260 + 140) + 20 = 400 + 20 = 420, по правилу прибавления суммы к числу.
170 + 100 + 150 = 170 + 250 = (150 + 20) + 250 = (150 + 250) + 20 = 400 = 20 = 420, по правилу прибавления суммы к числу.
130 + 140 + 150 = 270 + 150 = 270 + (130 + 20) = (270 + 130) = 20 = 400 + 20 = 420, по правилу прибавления суммы к числу.
110 + 140 + 170 = 170 + 250 = (150 + 20) + 250 = (150 + 250) + 20 = 400 = 20 = 420, по правилу прибавления суммы к числу.
Оформляем задание в тетрадь.

Сравни площади фигур.

Площадь второй фигуры больше, чем площадь первой фигуры. S1 – 11 клеток; S2 – 14 клеток.
Чтобы понять, площадь какой фигуры больше, нужно для начала вычислить их. Но из-за того, что фигуры сложные, т.е. для вычисления их площадей не существует формул, то придется считать клетки или воспользоваться палеткой.
Помни, что две половинки клетки в сумме дают одну клетку.
Рассмотрим первую фигуру и вычислим ее площадь.

6 полных клеток и 10 половинок клеток.
Согласно правилу подсчета клеток, количество неполных делим на два и прибавляем к количеству полных.
Тогда, 6 + (10 : 2) = 6 + 5 = 11 кл.
Рассмотрим вторую фигуру и вычислим ее площадь.
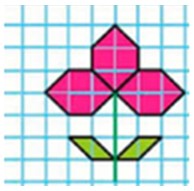
6 полных клеток и 16 половинок клеток.
Согласно правилу подсчета клеток, количество неполных делим на два и прибавляем к количеству полных.
Тогда, 6 + (16 : 2) = 6 + 8 = 14 кл.
Сравним площади фигур.
11 < 14, значит, что площадь второй фигуры больше, чем площадь первой.
Номер 310.
Масса тыквы, арбуза и дыни вместе 16 кг, масса тыквы и арбуза 13 кг, масса арбуза и дыни 8 кг. Найди массу дыни, арбуза и тыквы в отдельности.

1) 16 − 8 = 8 (кг) – тыква.
2) 16 − 13 = 3 (кг) – дыня.
3) 8 − 3 = 5 (кг) – арбуз.
Ответ: масса тыквы составляет 8 кг, масса дыни составляет 3 кг, масса арбуза составляет 5 кг.
Номер 311.
В трёх школах 1945 учеников. В первой и второй школах вместе 1225 учеников, а во второй и третьей — 1300 учеников. Сколько учеников в каждой школе? Реши и проверь решение.
Ответ:
1) 1945 − 1225 = 720 (уч.) – в 3-ей школе.
2) 1945 − 1300 = 645 (уч.) – в 1-ой школе.
3) 1300 − 720 = 580 (уч.) – во 2-ой школе.
Ответ: 720 учеников в третьей школе, 645 ученика в первой школе, 580 учеников во второй школе
1) 720 + 645 + 580 = 1945 (уч.)
Проверка: 720 + 645 + 580 = 1945 (уч.)
Номер 312.
Расставь скобки, чтобы равенства стали верными.
Ответ:
Номер 313.
Реши задачи, составив уравнения.
1) Разность неизвестного числа и числа 80 равна сумме чисел 360 и 140. Найди неизвестное число. 2) Из числа 430 вычли задуманное число и получили частное чисел 640 и 8. Какое число задумали?
Ответ:1)

2)

Номер 314.
Расстояние между двумя посёлками 96 км. Мотоциклист отправился из первого посёлка и проехал до остановки четвёртую часть пути. Сколько километров ему осталось проехать?

1) 96 : 4 = 24 (км) — проехал мотоциклист.
2) 96 − 24 = 72 (км) — осталось.
Ответ: 72 км дороги осталось проехать мотоциклисту.
Номер 315.
Ответ:2000 см2 = 20 дм2.
3 ч 10 мин = 190 мин.
45 ц = 4500 кг.
23 т = 23000 кг.
23 км = 23000 м.
600 с = 10 мин.
Номер 316.
Ответ:
Задание внизу страницы.
Ответ:
Задание на полях страницы.
Магический квадрат.


Проверка: 130 + 120 + 170 = 300 + 120 = 420 180 + 140 + 100 = 320 + 100 = 420 110 + 160 + 150 = 110 + 310 = 420 130 + 180 + 110 = 310 + 110 = 420 120 + 140 + 160 = 260 + 160 = 420 170 + 100 + 150 = 320 + 100 = 420 130 + 140 + 150 = 270 + 150 = 420 110 + 140 + 170 = 250 + 170 = 420
Сравни площади фигур.

Площадь второй фигуры больше, чем площадь первой фигуры. S1 – 11 клеток; S2 – 14 клеток.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.