Математика 4 класс учебник Моро, Бантова 1 часть ответы – страница 65

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 296.
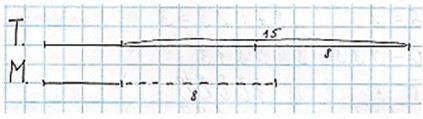
Какую часть отрезка АВ составляет отрезок CD на чертеже 1? отрезок МК на чертеже 2?

На первом рисунке CD составляет одну третью длины AB. На втором рисунке МК составляет две третьих или четыре шестых длины АВ.
Доля – одна часть из тех, на которые разделили целое. Например, если целое разделили на 4 части, то доля – это одна четвертая, т.е. одна часть из четырех.
Одна вторая – половина целого.
Одна третья – третья часть от целого.
Одна четвертая – четвертинка или четвертая часть от целого.
Одна пятая – пятая часть от целого и т.д.
Первое слово в названии долей указывает на количество долей, которые взяли, а второе – на сколько частей разделили целое.
Рассмотрим первый отрезок.
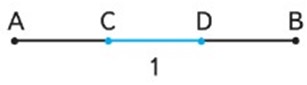
Отрезок АВ разбит на 3 отрезка: АС, CD и DB, каждому из которых соответствует единичный отрезок. Три отрезка, а СD – одна часть из трех частей. Значит, одна третья.
Рассмотрим второй отрезок.
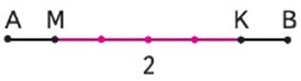
Отрезок АВ разбит на 6 единичных отрезков. Отрезку АМ и КВ соответствуют по одному единичному отрезку, а отрезку МК – 4 единичных отрезка. Значит, четыре отрезка из шести, т.е. четыре шестых.
Оформляем задание в тетрадь.
На первом рисунке CD составляет одну третью длины AB.
На втором рисунке МК составляет две третьих или четыре шестых длины АВ.
Номер 297.
Начерти отрезок, длина восьмой части которого 8 мм.
Ответ:8 ∙ 8 = 64 (мм) – длина отрезка. 64 мм = 6 см 4 мм

Доля – одна часть из тех, на которые разделили целое. Например, если целое разделили на 4 части, то доля – это одна четвертая, т.е. одна часть из четырех.
Одна вторая – половина целого.
Одна третья – третья часть от целого.
Одна четвертая – четвертинка или четвертая часть от целого.
Одна пятая – пятая часть от целого и т.д.
Первое слово в названии долей указывает на количество долей, которые взяли, а второе – на сколько частей разделили целое.
Оформляем условие в виде схематического чертежа.
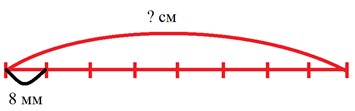
Рассуждаем.
Одна восьмая часть отрезка – 8 мм. Одна восьмая, т.е. одна часть из восьми. Значит, что целый отрезок разбили на 8 частей, а длина одной части 8 мм. Чтобы узнать, какова длина всего отрезка, нужно длину одной части умножить на количество частей.
8 ∙ 8 = 64 (мм) – длина отрезка.
64 мм = 6 см 4 мм.
Чертим отрезок.

Оформляем задание в тетрадь.
8 ∙ 8 = 64 (мм) – длина отрезка.
64 мм = 6 см 4 мм.

Номер 298.
Найди площадь прямоугольника ABCD в квадратных сантиметрах.
1) На сколько равных треугольников разделён прямоугольник ABCD? 2) Найди площадь закрашенной части прямоугольника. 3) Найди площадь не закрашенной части прямоугольника.

S = 2 ∙ 6 = 12 см2
1) Прямоугольник разделён на 12 равных треугольников.
12 : 12 = 1 см2;
2) 5 ∙ 1 = 5 см2 – площадь закр. части.
3) 12 - 5 = 7 см2 – площадь незакрытой части.
Площадь фигуры – часть плоскости, занятая фигурой. Площадь может измеряться в единицах измерения: мм2, см2, дм2, м2, км2 и др.
Площадь прямоугольника – произведение длин его сторон. Вычисляется по формуле: а · в, где а и в – стороны прямоугольника.
Рассмотрим прямоугольник и найдем его площадь.

ABCD – прямоугольник.
АВ = СD = 6 см.
BC = АD = 2 см.
S = ? см2.
S = АВ · BC.
S = 6 см · 2 см = 12 см2.
Ответим на первый вопрос.
Посчитаем количество равных частей, на которые разделен прямоугольник, т.е. практическим методом.
Мы узнали, что равных частей – 12 штук.
Они равны, т.е. их площади одинаковы, а при наложении фигуры совпадают.
Тогда, чтобы узнать, чему равна площадь одной части, нужно общую площадь разделить на количество равных частей.
Получается, 12 см2 : 12 = 1 см2 – площадь одной части.
Ответим на второй вопрос.
Закрашены 5 частей. Площадь одной части – 1 см2, а общая площадь неизвестна. Но она складывается из площади частей, из которых она состоит. Значит, площадь одной части умножаю на количество частей.
Тогда, 1см2 · 5 = 5 см2.
Ответим на третий вопрос.
Площадь не закрашенной части можно найти двумя способами: способами:
Способ 1
Общая площадь фигуры складывается из площади закрашенной части и не закрашенной. Значит, чтобы узнать, чему равна площадь не закрашенной части, нужно из общей площади фигуры вычесть площадь закрашенной.
Тогда, 12 см2 – 5 см2 = 7 см2.
Способ 2
Не закрашенную часть составляют 7 частей, общая площадь которых складывается из площади каждой части. Значит, чтобы узнать, чему равна площадь не закрашенной части, умножаю площадь части на их количество.
Тогда, 1 см2 · 7 = 7 см2.
Номер 299.
Для школы купили 5 мотков электрического провода, по 56 м в каждом. Израсходовали две седьмых части всего провода. Сколько метров провода осталось?
Ответ:Всего 5 м. по 56 м – 7 частей.
Израсходовали – 2 части.
Осталось – ? м.
1) 5 ∙ 56 = 280 (м) – провода купили.
2) 280 : 7 = 40 (м) – в 1 части.
3) 40 ∙ 2 = 80 (м) – израсходовали.
4) 280 − 80 = 200 (м).
Ответ: 200 метров провода осталось после ремонта.
Доля – одна часть из тех, на которые разделили целое. Например, если целое разделили на 4 части, то доля – это одна четвертая, т.е. одна часть из четырех.
Одна вторая – половина целого.
Одна третья – третья часть от целого.
Одна четвертая – четвертинка или четвертая часть от целого.
Одна пятая – пятая часть от целого и т.д.
Первое слово в названии долей указывает на количество долей, которые взяли, а второе – на сколько частей разделили целое.
Помни о зависимости между частью и целым:
часть + часть = целое.
целое – 1 часть = 2 часть.
целое – 2 часть = 1 часть.
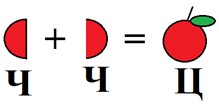
Оформляем условие в виде краткой записи.
Всего 5 м. по 56 м – 7 частей.
Израсходовали – 2 части.
Осталось – ? м.
Рассуждаем.
Чтобы узнать, сколько всего провода было куплено, складываем количество провода каждого мотка.
1) 5 ∙ 56 = 280 (м) – провода купили.
Продолжаем рассуждение.
Узнаем, сколько провода в одной части мотка. Для этого, разделим длину всего провода 7 частей.
2) 280 : 7 = 40 (м) – в 1 части.
Продолжаем рассуждение.
Чтобы узнать, сколько метров провода израсходовали, нужно длину одной части умножить на 2, потому что известно, что израсходовали 2 части.
3) 40 ∙ 2 = 80 (м) – израсходовали.
Продолжаем рассуждение.
Чтобы узнать, сколько провода осталось, из общей длины провода вычитаю длину израсходованной.
4) 280 − 80 = 200 (м).
Записываем ответ.
Ответ: 200 метров провода осталось.
Номер 300.
За 3 ч работы бульдозер разровнял 234 м2 дороги. Сколько квадратных метров дороги разровняет бульдозер за 10 ч, если будет работать с такой же производительностью?
Ответ:.jpg)
1) 234 : 3 = 78 (м2) – за 1 час.
2) 78 ∙ 10 = 780 (м2).
Ответ: 780 м2 дороги разровняет бульдозер за 10 часов.
Помни о том, каков конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а · 3, а – первый множитель, а 3 – количество множителей.
Помни о зависимости между компонентами и результатом действия умножения:
1 множитель · 2 множитель = значение произведения.
Значение произведения : 1 множитель = 2 множитель.
Значение произведения : 2 множитель = 1 множитель.
Данная задача: вида «объем работы в 1 час, количество часов, общий объем работы» характеризуется зависимостями между компонентами:
Объем работы в 1 час · количество часов = общий объем работы.
Общий объем работы : количество часов = объем работы в 1 час.
Общий объем работы : объем работы в 1 час = количество часов.
Оформляем условие в виде таблицы.

Рассуждаем.
Чтобы узнать, какую работу бульдозер выполняет в час, необходимо общий объем работы разделить на количество часов.
1) 234 : 3 = 78 (м2) – за 1 час.
Продолжаем рассуждение.
Чтобы узнать, какую работу бульдозер выполняет за 10 часов, необходимо объем работы в 1 час умножить на количество часов.
2) 78 ∙ 10 = 780 (м2).
Записываем ответ.
Ответ: 780 м2 разровняет за 10 часов.
Решение выражением:
(234 : 3) · 10, где 234 : 3 – объем выполняемой работы в 1 час.
Номер 301.
Ответ:92 : 46 = 2 87 : 29 = 3

Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий. Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
Помни о том, что существует алгоритм письменного деления. Следуй ему, объясняя, как выполняешь деление:
1) Выделю первое неполное делимое, чтобы определить количество цифр в частном.
2) Нахожу цифру сотен в частном:
3) Нахожу, сколько сотен разделили:
4) Нахожу, сколько сотен осталось разделить:
5) Образую второе неполное делимое:
6) Нахожу, количество десятков в частном:
7) Нахожу, сколько десятков разделили:
8) Нахожу, сколько десятков осталось разделить:
9) Образую третье неполное делимое:
10) Нахожу количество единиц в частном:
11) Нахожу, сколько единиц разделили:
12) Нахожу, сколько единиц осталось разделить:
13) Читаю ответ.
Помни о том, что существует алгоритм объяснения умножения трехзначного числа на однозначное. Следуй ему:
1) Записываю первый множитель так, чтобы каждая цифра стояла в своей клетке. Ставлю знак умножить;
2) Записываю второй множитель так, чтобы разряд стоял под разрядом;
3) Провожу черту, обозначающую знак равно;
4) Умножение начинаю с единиц низшего разряда;
5) Умножаю десятки;
6) Умножаю сотни;
7) Умножение окончено. Читаю ответ.
Следуй плану при устном объяснении вычитания в столбик:
1) Записываю уменьшаемое так, чтобы каждая цифра стояла в своей клетке. Ставлю знак минус;
2) Записываю вычитаемое так, чтобы разряд стоял под разрядом;
3) Провожу черту, обозначающую знак равно;
4) Вычитание начинаю с единиц низшего разряда. Вычитаю единицы;
5) Вычитаю десятки;
6) Вычитаю сотни;
7) Вычитание окончено. Читаю ответ.
Выполняем вычисления по действиям.
92 : 46 = 2 (вычисляем путём подбора)
87 : 29 = 3 (вычисляем путём подбора)
10 000 – 935 : 5 = 9 813

20 000 – 198 · 4 = 19 208
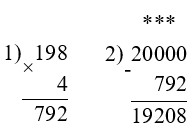
7 · (948 – 833) : 5 = 161
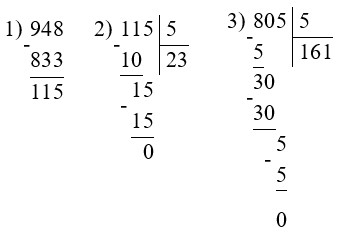
(159 + 837) : 6 · 4 = 664
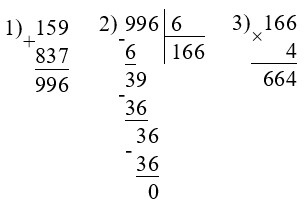
Оформляем задание в тетрадь.
92 : 46 = 2
87 : 29 = 3

Номер 302.
Проверь правильно ли выполнено деление с остатком.
Ответ:

Вспомни названия компонентов действия деления и зависимость между компонентами и результатами действия деления:
Делимое : делитель = значение частного.
Значение частного · делитель = делимое.
Делимое : значение частного = делитель.
Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий. Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Рассуждаем.
Самопроверкой в ходе и результате вычислений является то, что: 1) Мы постоянно сравниваем остаток с делителем. Он всегда должен быть меньше делителя. В противном случае деление выполнении неверно или не завершено; 2) Мы проверяем, правильно ли подобрана цифра того или иного разряда через умножение на делитель. Цифра единиц разряда подобрана верно тогда, когда число от умножения меньше чем неполное делимое. 3) Мы получаем искомое число, выполняя умножения результата деления на делитель и прибавления остатка. Если число и делимое совпали, то деление выполнено верно. В противном случае, была допущена ошибка.
Выполняем вычисления и проверку.
76 : 8 = 9 (ост. 6)
1) 6 < 8
2) 9 · 8 = 72
3) 72 + 6 = 78
78 > 76, неверно.
793 : 6 = 132 (ост. 1)
1) 1 < 6
2) 132 · 6 = 792
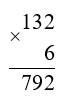
3) 792 + 1 = 793
793 = 793, верно.
54 : 11 = 4 (ост. 10)
1) 10 < 11
2) 11 · 4 = 44
3) 44 + 10 = 54
54 = 54, верно.
612 : 7 = 87 (ост. 4)
1) 4 < 7
2) 87 · 7 = 609
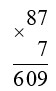
3) 609 + 4 = 613
613 > 612, неверно.
Оформляем задание в тетрадь.


Номер 303.
Лимоны раскладывали в корзины, по 100 штук в каждую. Сколько было лимонов, если их разложили в 15 корзин и еще осталось 30 лимонов?
Ответ:Всего – ? шт.
Разложили – 15 к. по 100 шт.
Осталось – 30 шт.
1) 100 ∙ 15 = 1500 (шт.) – разложили.
2) 1500 + 30 = 1530 (шт.).
100 ∙ 15 + 30 = 1530 (шт.).
Ответ: 1530 лимонов всего было.
Помни о том, каков конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а · 3, а – первый множитель, а 3 – количество множителей.
Помни о зависимости между компонентами и результатом действия умножения:
1 множитель · 2 множитель = значение произведения.
Значение произведения : 1 множитель = 2 множитель.
Значение произведения : 2 множитель = 1 множитель.
Данная задача: вида «кол-во лимонов в 1 корзине, кол-во корзин, общее количество лимонов» характеризуется зависимостями между компонентами:
Кол-во лимонов в 1 корзине · кол-во корзин = общее кол-во лимонов.
Общее кол-во лимонов : кол-во корзин = кол-во лимонов в 1 корзине.
Общее кол-во лимонов : кол-во лимонов в 1 корзине = кол-во корзин.
Оформляем условие в виде краткой записи.
Всего – ? шт.
Разложили – 15 к. по 100 шт.
Осталось – 30 шт.
Рассуждаем.
Чтобы узнать, сколько всего лимонов разложили, необходимо количество лимонов одной корзины умножить на количество корзин.
1) 100 ∙ 15 = 1500 (шт.) – разложили.
Продолжаем рассуждение.
Мы узнали, что в корзины разложили 1500 лимонов и еще 30 осталось. Общее количество лимонов складывается из количества разложенных лимонов и оставшихся. Значит, чтобы узнать, сколько лимонов было, нужно сложить количество разложенных и оставшихся.
2) 1500 + 30 = 1530 (шт.).
Записываем ответ.
Ответ: 1530 лимонов было.
Решение выражением: 100 ∙ 15 + 30 = 1530 (шт.).
Номер 304.
Сравни значения величин.
Ответ:5 м = 50 дм 5 м2 > 50 дм2
(50 дм = 50 дм) (500 дм2 > 50 дм2)
400 м < 1 км 400000 м2 < 1 км2
(400 м < 1000 м) (400000 м2 < 1000000 м2)
Длина – величина, характеризующая протяженность объекта на плоскости, выражается в таких единицах измерения, как миллиметр, сантиметр, дециметр, метр, километр.
Помни о соотношении числовых значений единиц измерения длины:
1 см = 10 мм.
1 дм = 10 см.
1 м = 100 см.
1 м = 10 дм.
1 км = 1000 м.
Площадь – величина, которая характеризует размер части плоскости, занятой фигурой. Измеряется в таких единицах измерения, как: мм2, см2, дм2, м2, км2 и др.
Помни о соотношении числовых значений единиц измерения площади:
1 см2 = 100 мм2.
1 дм2 = 100 см2.
1 м2 = 10 000 см2.
1 м2 = 100 дм2.
Сравниваем значения величин.
5 м и 50 дм
5м; 1 м – 10 дм, значит, 10 дм · 5 = 50 дм
50 дм = 50 дм
Значит, 5 м = 50 дм
400 м и 1 км
1 км; 1 км – 1000 м
400 м > 1000
Значит, 400 м > 1000 м
5 м2 и 50 дм2
5 м2; 1 м2 – 100 дм2, потому что 10 дм · 10 дм = 100 дм2, значит, 100 дм2 · 5 = 500 дм2
500 дм2 > 50 дм2
Значит, 5 м2 > 50 дм2
400 000 м2 и 1 км2
1 км2; 1 км2 – это 1 000 000 м2, потому что 1 000 м · 1 000 м = 1 000 000 м2
400 000 м2 < 1 000 000 м2
Значит, 400 000 м2 < 1 км2
Оформляем задание в тетрадь.
5 м = 50 дм
(50 дм = 50 дм)
5 м2 > 50 дм2
(500 дм2 > 50 дм2)
400 м < 1 км
(400 м < 1000 м)
400000 м2 < 1 км2
(400000 м2 < 1000000 м2)
Номер 305.
Таня нашла на 15 орехов больше, чем Марина. Таня отдала Марине 8 орехов. У кого из девочек стало больше орехов и на сколько?
Ответ:1-й способ решения:

1) 15 – 8 = 7 (ор.) – у Тани.
2) 8 – 7 = 1 (ор.)
Ответ: у Марины на 1 орех больше, чем у Тани.
2-й способ решения:
Если Таня отдала 8 орехов Марине, значит у Тани стало на 8 орехов меньше, а у Марины на 8 орехов больше.
8 + 8 – 15 = 16 – 15 = 1 (ор.) – разница между Таней и Мариной.
Ответ: на 1 орех.
Оформляем условие задачи в виде схематического чертежа.
Оформляем условие в виде схематического чертежа.
Рассуждаем.
После того, как Таня отдала Марине орехи, то:
1) 15 – 8 = 7 (ор.) – осталось из разницы в 15 орехов.
Продолжаем рассуждение.
Так как у Марины стало на 8 орехов больше, то:
2) 8 – 7 = 1 (ор.) – у Марины стало на один орех больше, чем у Тани.
Записываем ответ.
Ответ: у Марины стало на 1 орех больше.
Задание внизу страницы.
Начерти отрезок, длина третьей части которого 20 мм.
Ответ:20 ∙ 3 = 60 мм. 60 мм = 6 см.

Доля – одна часть из тех, на которые разделили целое. Например, если целое разделили на 4 части, то доля – это одна четвертая, т.е. одна часть из четырех.
Одна вторая – половина целого.
Одна третья – третья часть от целого.
Одна четвертая – четвертинка или четвертая часть от целого.
Одна пятая – пятая часть от целого и т.д.
Первое слово в названии долей указывает на количество долей, которые взяли, а второе – на сколько частей разделили целое.
Оформляем условие в виде схематического чертежа.
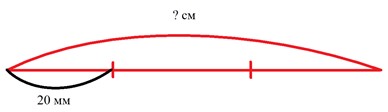
Рассуждаем.
Длина третьей части отрезка – 20 мм. Третья часть, значит, одна из трех. Получается, чтобы узнать длину всего отрезка, нужно умножить длину одной части на количество частей.
Тогда, 20 мм · 3 = 60 мм или 6 см, потому что 1 см = 10 мм.
Оформляем задание в тетрадь.
20 ∙ 3 = 60 мм.
60 мм = 6 см.

Номер 300.
Какую часть отрезка АВ составляет отрезок CD на чертеже 1? отрезок МК на чертеже 2?

На первом рисунке CD составляет одну третью длины AB. На втором рисунке МК составляет две третьих или четыре шестых длины АВ.
Номер 301.
Начерти отрезок, длина восьмой части которого 8 мм.
Ответ:8 ∙ 8 = 64 (мм) – длина отрезка. 64 мм = 6 см 4 мм

Номер 302.
Найди площадь прямоугольника ABCD в квадратных сантиметрах.
1) На сколько равных треугольников разделён прямоугольник ABCD? 2) Найди площадь закрашенной части прямоугольника. 3) Найди площадь не закрашенной части прямоугольника.

S = 2 ∙ 6 = 12 см2
1) Прямоугольник разделён на 12 равных треугольников.
12 : 12 = 1 см2;
2) 5 ∙ 1 = 5 см2 – площадь закр. части.
3) 12 - 5 = 7 см2 – площадь незакрытой части.
Номер 303.
Для школы купили 5 мотков электрического провода, по 56 м в каждом. Израсходовали две седьмых части всего провода. Сколько метров провода осталось?
Ответ:Всего 5 м. по 56 м – 7 частей
Израсходовали – 2 части
Осталось – ? м
1) 5 ∙ 56 = 280 (м) – провода купили.
2) 280 : 7 = 40 (м) – в 1 части.
3) 40 ∙ 2 = 80 (м) – израсходовали.
4) 280 − 80 = 200 (м)
Ответ: 200 метров провода осталось всего после ремонта.
Номер 304.
За 3 ч работы бульдозер разровнял 234 м2 дороги. Сколько квадратных метров дороги разровняет бульдозер за 10 ч, если будет работать с такой же производительностью?
Ответ:.jpg)
1) 234 : 3 = 78 (м2) – за 1 час.
2) 78 ∙ 10 = 780 (м2)
Ответ: 780 м2 дороги разровняет за 10 часов.
Номер 305.
Ответ:92 : 46 = 2 87 : 29 = 3

Номер 306.
Проверь правильно ли выполнено деление с остатком.
Ответ:

Номер 307.
Лимоны раскладывали в корзины, по 100 штук в каждую. Сколько было лимонов, если их разложили в 15 корзин и еще осталось 30 лимонов?
Ответ:Всего – ? шт.
Разложили – 15 к. по 100 шт.
Осталось – 30 шт.
1) 100 ∙ 15 = 1500 (шт.) – разложили.
2) 1500 + 30 = 1530 (шт.)
100 ∙ 15 + 30 = 1530 (шт.)
Ответ: 1530 лимонов было всего.
Номер 308.
Сравни значения величин.
Ответ:5 м = 50 дм 5 м2 > 50 дм2
(50 дм = 50 дм) (500 дм2 > 50 дм2)
400 м < 1 км 400000 м2 < 1 км2
(400 м < 1000 м) (400000 м2 < 1000000 м2)
Номер 309.
Таня нашла на 15 орехов больше, чем Марина. Таня отдала Марине 8 орехов. У кого из девочек стало больше орехов и на сколько?
Ответ:
1) 15 − 8 = 7 (ор.) – у Тани.
2) 8 − 7 = 1 (ор.)
Ответ: у Марины на 1 орех больше, чем у Тани.
Задание внизу страницы.
Начерти отрезок, длина третьей части которого 20 мм.
Ответ:20 ∙ 3 = 60 мм. 60 мм = 6 см.

С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.