Математика 4 класс учебник Моро, Бантова 1 часть ответы – страница 42

Учебник 1 часть. Математика 4 класс. Учебник Моро.

Тип: ГДЗ, Решебник.
Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
Часть: 1.
Год: 2020-2024.

Серия: Школа России (ФГОС).
Издательство: Просвещение.

Автор

Материал подготовила:

Ольга Дмитриева

Отличается задание? Переключите год учебника.

2020 2023

математика 4 класс Моро, Бантова - 1 часть страница 42

Номер 185.

1) В магазин привезли 48 коробок с зелёным и чёрным виноградом. В 16 коробках был чёрный виноград, по 9 кг в каждой, а в остальных – зелёный, по 8 кг в каждой. Сколько всего килограммов винограда привезли в магазин?
2) В магазин привезли 400 кг зелёного и чёрного винограда. В нескольких коробках был чёрный виноград по 9 кг в каждой, а в 32 коробках – зелёный виноград, по 8 кг в каждой. Сколько коробок чёрного винограда привезли в магазин?

Ответ:

Задача 1:

математика 4 класс Моро, Бантова - 1 часть страница 42, номер 185-2

1) 9 ∙ 16 = 144 (кг) – черный виноград. 2) 48 − 16 = 32 (к.) – с зелёным виноградом. 3) 8 ∙ 32 = 256 (кг) – зеленый виноград. 4) 144 + 256 = 400 (кг)
Ответ: 400 кг чёрного винограда всего привезли всего в магазин.
Задача 2:

математика 4 класс Моро, Бантова - 1 часть страница 42, номер 185-4

1) 8 ∙ 32 = 256 (кг) – зеленого винограда. 2) 400 − 256 = 144 (кг) – черного винограда. 3) 144 : 9 = 16 (к.)
Ответ: 16 коробок с черным виноградом всего привезли в магазин.

Подсказка:

Помним конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а · 3, а – первый множитель, а 3 – количество множителей.
Помним о зависимости между компонентами и результатом действия умножения:

   1 множитель · 2 множитель = значение произведения.
   Значение произведения : 1 множитель = 2 множитель.
   Значение произведения : 2 множитель = 1 множитель.

Данная задача характеризуется зависимостями между компонентами:

   Масса 1 ящика · количество ящиков = общее количество винограда.
   Общее количество винограда : масса 1 ящика = количество ящиков.
   Общее количество винограда : количество ящиков = масса 1 ящика.

Задача 1.

Шаг 1.
Оформляем условие в виде таблицы.

Шаг 2.
Рассуждаем.

Общее количество винограда складывается из количества винограда каждого ящика, при этом количества винограда в одном ящике одинаково. Значит, чтобы узнать, сколько всего винограда было, нужно массу одного ящика умножаю на количество ящиков.
1) 9 ∙ 16 = 144 (кг) – черный виноград.

Шаг 3.
Продолжаем рассуждение.

Общее количество коробок складывается из количество коробок с черным виноградом и зеленым. Значит, чтобы узнать, сколько коробок в зеленым виноградом было, нужно из общего количества коробок вычесть количество коробок с черным виноградом.
2) 48 – 16 = 32 (к.) – с зелёным виноградом.

Общее количество винограда складывается из количества винограда каждого ящика, при этом количества винограда в одном ящике одинаково. Значит, чтобы узнать, сколько всего винограда было, нужно массу одного ящика умножаю на количество ящиков.
3) 8 ∙ 32 = 256 (кг) – зеленый виноград.

Шаг 4.
Продолжаем рассуждение.

Общее количество привезенного винограда складывается из количества привезенного зеленого и черного винограда. Значит, чтобы узнать, сколько винограда было привезено, нужно сложить количество привезенного винограда обоих видов.
4) 144 + 256 = 400 (кг).

Шаг 5.
Записываем ответ.

Ответ: 400 кг винограда всего.
Решение выражением: 8 · (48 – 16) + 9 · 16

Задача 2.

Шаг 1.
Оформляем условие в виде таблицы.

Шаг 2.
Рассуждаем.

Чтобы узнать, сколько килограммов зелёного винограда привезли, нужно массу одного ящика умножить на количество ящиков.
1) 8 ∙ 32 = 256 (кг) – зеленого винограда.

Шаг 3.
Продолжаем рассуждение.

Общее количество привезенного винограда складывается из количества привезенного зеленого и черного винограда. Значит, чтобы узнать, черного винограда привезли, нужно из общего количества винограда вычесть количество зеленого.
2) 400 – 256 = 144 (кг) – черного винограда.

Шаг 4.
Продолжаем рассуждение.

Нам известная масса одного ящика и общее количество винограда, а количество коробок – нет. При этом, общее количество винограда складывается из количества винограда каждого ящика. Значит, чтобы узнать, сколько ящиков с виноградом привезли, нужно общее количество винограда разделить на количество винограда в 1 ящике.
3) 144 : 9 = 16 (к.).

Шаг 5.
Записываем ответ.

Ответ: 16 коробок с черным виноградом.
Решение выражением: (400 – (8 · 32)) : 9 = 16 (к.)

Номер 186.

На своём приусадебном участке семья вырастила 56 кг огурцов, а перца – в 8 раз меньше, чем огурцов. На сколько килограммов перца было меньше, чем огурцов?

Ответ:

математика 4 класс Моро, Бантова - 1 часть страница 42, номер 186

1) 56 : 8 = 7 (кг) – перца. 2) 56 – 7 = 49 (кг)
Ответ: было на 49 кг перца меньше, чем огурцов.

Подсказка:

«в 8 раз меньше», значит, вычисляется делением.
Чтобы узнать, на сколько одно число меньше другого, нужно из большего числа вычесть меньшее. Вычисляется вычитанием.

Шаг 1.
Оформляем условие в виде краткой записи.

Шаг 2.
Рассуждаем.

Семья вырастила 56 кг огурцов, а перца – в 8 раз меньше. Значит, чтобы узнать, сколько было выращено перца, нужно общее количество огурцов разделить на 8.
1) 56 : 8 = 7 (кг) – перца.

Шаг 3.
Продолжаем рассуждение.

Чтобы узнать, на сколько одно число больше другого, нужно из большего числа вычесть меньшее. Значит, чтобы узнать, на сколько кг меньше было выращено перца, чем огурца, нужно из количества огурцов вычесть количество перца.
2) 56 – 7 = 49 (кг).

Шаг 4.
Записываем ответ.

Ответ: на 49 кг было перца меньше.
Решение выражением: 56 – (56 : 8) = 49 (кг)

Номер 187.

Сравни уравнения в каждом столбике и, не вычисляя, скажи, в котором из них неизвестное число больше. Проверь вычислением:

Ответ:

х + 37 = 78 х = 78 − 37 х = 41
х + 37 = 80 х = 80 − 37 х = 43
43 > 41 При одинаковом втором слагаемом, чем больше сумма уравнения, тем больше будет неизвестное число.
45 + х = 63 х = 63 − 45 х = 18
45 + х = 68 х = 68 − 45 х = 23
23 > 18 При одинаковом втором слагаемом, чем больше сумма уравнения, тем больше будет неизвестное число.
90 − х = 47 х = 90 − 47 х = 43
90 − х = 50 х = 90 − 50 х = 40
43 > 40 При одинаковом уменьшаемом, чем меньше разность в уравнении, тем больше будет неизвестное число.
х − 28 = 32 х = 32 + 28 х = 60
х − 28 = 22 х = 22 + 28 х = 50
60 > 50 При одинаковом уменьшаемом, чем меньше разность в уравнении, тем больше будет неизвестное число.

Подсказка:

Уравнение – равенство с неизвестной, при подстановке числа в которую, получается верное равенство.
Помним названия компонентов действия умножения, и зависимость между компонентами и результатом действия умножения:

   Уменьшаемое – вычитаемое = значение разности.
   Уменьшаемое – значение разности = вычитаемое.
   Значение разности + вычитаемое = уменьшаемое.

   1 слагаемое + 2 слагаемое = значение суммы.
   Значение суммы – 1 слагаемое = 2 слагаемое.
   Значение суммы – 2 слагаемое = 1 слагаемое.

Шаг 1.
Сравним.

х + 37 = 78, х – неизвестное слагаемое. Чтобы найти неизвестное слагаемое, нужно из значения суммы вычесть известное слагаемое.
х + 37 = 80, х – неизвестное слагаемое. Чтобы найти неизвестное слагаемое, нужно из значения суммы вычесть известное слагаемое.
При одинаковом втором слагаемом, чем больше сумма уравнения, тем больше будет неизвестное число.

45 + х = 63, х – неизвестное слагаемое. Чтобы найти неизвестное слагаемое, нужно из значения суммы вычесть известное слагаемое.
45 + х = 68, х – неизвестное слагаемое. Чтобы найти неизвестное слагаемое, нужно из значения суммы вычесть известное слагаемое.
При одинаковом втором слагаемом, чем больше сумма уравнения, тем больше будет неизвестное число.

90 – х = 47, х – неизвестное вычитаемое. Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть значение разности.
90 – х = 50, х – неизвестное вычитаемое. Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть значение разности.
При одинаковом уменьшаемом, чем меньше разность в уравнении, тем больше будет неизвестное число.

х – 28 = 32, х – неизвестное уменьшаемое. Чтобы найти неизвестное уменьшаемое, нужно к значению разности прибавить вычитаемое.
х – 28 = 22, х – неизвестное уменьшаемое. Чтобы найти неизвестное уменьшаемое, нужно к значению разности прибавить вычитаемое.
При одинаковом уменьшаемом, чем меньше разность в уравнении, тем больше будет неизвестное число.

Шаг 2.
Проверим вычислениями.

х + 37 = 78
х = 78 – 37
х = 41
х + 37 = 80
х = 80 – 37
х = 43
43 > 41

45 + х = 63
х = 63 – 45
х = 18
45 + х = 68
х = 68 – 45
х = 23
23 > 18

90 – х = 47
х = 90 – 47
х = 43
90 – х = 50
х = 90 – 50
х = 40
43 > 40

х – 28 = 32
х = 32 + 28
х = 60
х − 28 = 22
х = 22 + 28
х = 50
60 > 50

Номер 188.

Ответ:

1) 1 000 000 : 1 000 − 999 = 1 000 − 999 = 1 1 000 000 : 1 000 + 1 = 1 000 + 1 = 1 001 420 000 − 20 000 = 400 000 28 000 : 4 ∙ 100 = 7 000 ∙ 100 = 700 000
2)

математика 4 класс Моро, Бантова - 1 часть страница 42, номер 188

Подсказка:

Помним о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Разделить число на 1000, значит, уменьшить его в 1000 раз, т.е. убрать в записи числа три нуля.
Умножить на 100, значит, увеличить его в 100 раз, т.е. приписать к записи числа два нуля.
Помним алгоритм объяснения умножения трехзначного числа на однозначное:

1) Записываю первый множитель так, чтобы каждая цифра стояла в своей клетке. Ставлю знак умножить;
2) Записываю второй множитель так, чтобы разряд стоял под разрядом;
3) Провожу черту, обозначающую знак равно;
4) Умножение начинаю с единиц низшего разряда;
5) Умножаю десятки;
6) Умножаю сотни;
7) Умножение окончено. Читаю ответ.

Следуйте плану при устном объяснении вычитания в столбик:

1) Записываю уменьшаемое так, чтобы каждая цифра стояла в своей клетке. Ставлю знак минус;
2) Записываю вычитаемое так, чтобы разряд стоял под разрядом;
3) Провожу черту, обозначающую знак равно;
4) Вычитание начинаю с единиц низшего разряда. Вычитаю единицы;
5) Вычитаю десятки;
6) Вычитаю сотни;
7) Вычитание окончено. Читаю ответ.

Помним алгоритм письменного деления:

1) Выделю первое неполное делимое, чтобы определить количество цифр в частном.
2) Нахожу цифру сотен в частном:
3) Нахожу, сколько сотен разделили:
4) Нахожу, сколько сотен осталось разделить:
5) Образую второе неполное делимое:
6) Нахожу, количество десятков в частном:
7) Нахожу, сколько десятков разделили:
8) Нахожу, сколько десятков осталось разделить:
9) Образую третье неполное делимое:
10) Нахожу количество единиц в частном:
11) Нахожу, сколько единиц разделили:
12) Нахожу, сколько единиц осталось разделить:
13) Читаю ответ

Шаг 1.
Расставляем порядок действий и выполняем вычисления.

1 000 000 : 1 000 – 999 = 1
1) 1 000 000 : 1 000 = 1 000
2) 1 000 – 999 = 1

1 000 000 : 1 000 + 1 = 1 001
1) 1 000 000 : 1 000 = 1 000
2) 1 000 + 1 = 1 001, потому что если к любому числу прибавить единицу, то получится число следующее за данным.

420 000 – 20 000 = (400 000 + 20 000) – 20 000 = 400 000 + (20 000 – 20 000) = 400 000, по правилу вычитания числа из суммы.

28 000 : 4 · 100 = 700 000
1) 28 000 : 4 = 7 000
2) 7 000 · 100 = 700 000

Шаг 2.
Оформляем задание в тетрадь.

Номер 189.

Игра «Отгадай число». Задумай любое однозначное число, кроме нуля. Умножь его на 5. Произведение увеличь в 2 раза. К результату прибавь 14. Из суммы вычти 8. Отбрось первую слева цифру результата. Оставшееся число умножь на 7 и раздели на 2. Объясни, почему в результате всегда будет 21.

Ответ:

Задуманное число 7. 7 ∙ 5 = 35 35 ∙ 2 = 70 70 + 14 = 84 84 − 8 = 76 6 ∙ 7 = 42 42 : 2 = 21
Задуманное число 3. 3 ∙ 5 = 15 15 ∙ 2 = 30 30 + 14 = 44 44 − 8 = 36 6 ∙ 7 = 42 42 : 2 = 21
При умножении числа на 5, затем на 2 получается двухзначное число, оканчивающееся на 0. При прибавлении 14, затем вычитании 8, получается двухзначное число оканчивающееся на 6. Соответственно при отбрасывании первой цифры слева оставшееся число равно 6. 6 ∙ 7 = 42 42 : 2 = 21

Подсказка:

Следуй плану, выполняй действия, пытайся заметить закономерность и объяснить, почему всегда получается число 21.
1. Умножь на 5 значит, увеличь в 5 раз – вычисляется умножением.
2. Увеличь в 2 раза, значит, умножь на 2 – вычисляется умножением.
3. Прибавь 14, т.е. увеличь число на 14 единиц, вычисляется сложением.
4. Вычти 8, т.е. уменьши число на 8 единиц. Вычисляется вычитанием.
5. Отбрось первую слева цифру результата – т.е. цифру высшего разряда.
6. Умножь на 7, т.е. увеличь в 7 раз, вычисляется умножением.
7. Раздели на 2, т.е. уменьши в 2 раза, вычисляется делением.

Шаг 1.
Сыграем в «Отгадай число».

Задуманное число 7.
7 ∙ 5 = 35
35 ∙ 2 = 70
70 + 14 = 84
84 − 8 = 76
6 ∙ 7 = 42
42 : 2 = 21

Задуманное число 3.
3 ∙ 5 = 15
15 ∙ 2 = 30
30 + 14 = 44
44 − 8 = 36
6 ∙ 7 = 42
42 : 2 = 21

Шаг 2.
Проанализируем.

Каждый раз мы следуем плану.
1) умножении на 5
    При умножении числа на 5 единиц может получиться 0 или 5, значит, общий вид числа: х5 или х0.
2) увеличить число в 2 раза, т.е. умножить на 2.
    При умножении числа на 2 с единицами, которые равны 5 или 0, получается, что в обоих случаях количество единиц обращается в 0, потому что 0 · 2 = 0 и 5 · 2 = 0 общий вид становится х0.
3) прибавить к числу 14.
    Мы работаем только с единицами, поэтому количество единиц в числе становится равно 4, потому что 0 + 14 = 14 - 1 дес. 4 ед. Общий вид становится: х4.
4) вычесть 8 единиц из числа, уменьшить на 8.
    Значит, х4 – 8 = х6, потому что мы занимаем десяток и получаем 14 ед., а 14 ед. - 8 ед. = 6 ед. Значит, теперь общий вид – х6.
5) отбрасываем первую слева цифру, т.е. цифру высшего разряда и получается, что общий вид теперь – число 6.
6) умножить число на 7
    Значит, 6 · 7 = 42. Общий Вид числа – 42
7) разделить число на 2. т.е. уменьшить в 2 раза.
    Значит, 42 : 2 = 21.

Шаг 3.
Сделаем вывод.

Вывод: все изменения количества единиц в числе приводят к тому, что в результате всегда получается 21.

Номер 190.

Вычислительная машина работает так, как показано на рисунке. Составь план её работы. Какое число будет получаться на выходе из машины, если на входе будет число 7; 8; 10; 200; 12; 158?

Ответ:

План работы вычислительной машины: 1. Вводится некоторое число; 2. Это число сравнивается с 100; 3. Если это число > 100, то оно сразу попадает на выход, а если число < 100, то сначала умножается на 6 и потом попадает на выход.
7 ∙ 6 = 42 8 ∙ 6 = 48 10 ∙ 6 = 60
200 = 200 12 ∙ 6 = 72 158 = 158

Подсказка:

Вычислительная машина – машина, которая производит некоторые числа с числом.
Проанализируйте ее схему, чтобы узнать, какие именно действия она производит и как изменяется число. Чтобы проверить правильность составления плана, введите в вычислительную машину число.

Шаг 1.
Составляем план работы.

План работы вычислительной машины:
1. Вводится некоторое число;
2. Это число сравнивается с 100;
3. Если это число > 100, то оно сразу попадает на выход, а если число < 100, то сначала умножается на 6 и потом попадает на выход.

Шаг 2.
Вычисления.

Проведем все числа через вычислительную машину по плану:

Если 7, то 7 < 100, значит, 7 · 6 = 42
Если 8, то 8 < 100, значит, 8 · 6 = 48
Если 10, то 10 < 100, значит, 10 · 6 = 60
Если 200, то 200 > 100, значит, 200
Если 12, то 12 < 100, значит, 12 · 6 = 72
Если 158, то 158 > 100, значит, 158

Задание внизу страницы.

Вычисли.

Ответ:

математика 4 класс Моро, Бантова - 1 часть страница 42, Задание внизу страницы

Подсказка:

Помним о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Помним алгоритм объяснения умножения трехзначного числа на однозначное:

1) Записываю первый множитель так, чтобы каждая цифра стояла в своей клетке. Ставлю знак умножить;
2) Записываю второй множитель так, чтобы разряд стоял под разрядом;
3) Провожу черту, обозначающую знак равно;
4) Умножение начинаю с единиц низшего разряда;
5) Умножаю десятки;
6) Умножаю сотни;
7) Умножение окончено. Читаю ответ.

Следуйте плану при устном объяснении вычитания в столбик:

1) Записываю уменьшаемое так, чтобы каждая цифра стояла в своей клетке. Ставлю знак минус;
2) Записываю вычитаемое так, чтобы разряд стоял под разрядом;
3) Провожу черту, обозначающую знак равно;
4) Вычитание начинаю с единиц низшего разряда. Вычитаю единицы;
5) Вычитаю десятки;
6) Вычитаю сотни;
7) Вычитание окончено. Читаю ответ.

Помним алгоритм письменного деления:

1) Выделю первое неполное делимое, чтобы определить количество цифр в частном.
2) Нахожу цифру сотен в частном:
3) Нахожу, сколько сотен разделили:
4) Нахожу, сколько сотен осталось разделить:
5) Образую второе неполное делимое:
6) Нахожу, количество десятков в частном:
7) Нахожу, сколько десятков разделили:
8) Нахожу, сколько десятков осталось разделить:
9) Образую третье неполное делимое:
10) Нахожу количество единиц в частном:
11) Нахожу, сколько единиц разделили:
12) Нахожу, сколько единиц осталось разделить:
13) Читаю ответ.

Шаг 1.
Расставляем порядок действий и выполняем вычисления.

900 – 756 : 9 – 84 = 732

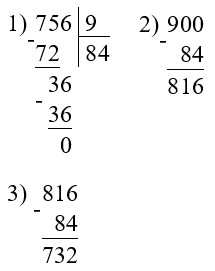
906 : 6 · 100 = 15 100

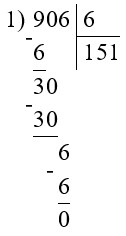
2) 151 · 100 = 15 100

1 000 – 806 = 194

Шаг 2.
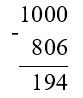
Оформляем задание в тетрадь.

Задание на полях страницы.

Какая фигура лишняя?

математика 4 класс Моро, Бантова - 1 часть страница 42, задание на полях

Ответ:

Лишней может быть: Тупоугольный треугольник, потому что остальные – остроугольные треугольники. Равносторонний треугольник, потому что остальные – неравносторонние. Синий треугольник, потому что остальные – зеленые треугольники.

Подсказка:

Для того, чтобы понять, какая фигура лишняя, проанализируй все по всем возможным признакам: цвет, форма, количество углов и виды, количество сторон и их вид, размер.

Шаг 1.
Рассуждаем.

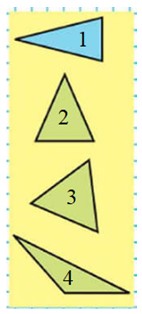
1. Голубой равнобедренный остроугольный треугольник.
2. Зеленый равнобедренный остроугольный треугольник.
3. Зеленый равнобедренный равносторонний остроугольный треугольник.
4. Зеленый разносторонний тупоугольный треугольник.

Шаг 2.
Сравним и сделаем вывод.

Таким образом, лишним может быть :
треугольник номер 1, потому что он единственный голубой;
треугольник номер 3, потому что он единственный равносторонний;
треугольник номер 4, потому что он не равнобедренный;
треугольник номер 4, потому что он единственный тупоугольный;

математика 4 класс Моро, Бантова - 1 часть страница 42. Год 2023

Номер 191.

1) В магазин привезли 48 коробок с зелёным и чёрным виноградом. В 16 коробках был чёрный виноград, по 9 кг в каждой, а в остальных – зелёный, по 8 кг в каждой. Сколько всего килограммов винограда привезли в магазин? 2) В магазин привезли 400 кг зелёного и чёрного винограда. В нескольких коробках был чёрный виноград по 9 кг в каждой, а в 32 коробках – зелёный виноград, по 8 кг в каждой. Сколько коробок чёрного винограда привезли в магазин?

Ответ:

Задача 1:

математика 4 класс Моро, Бантова - 1 часть страница 42. Год 2023. номер 191-2

1) 9 ∙ 16 = 144 (кг) – черный виноград. 2) 48 − 16 = 32 (к.) – с зелёным виноградом. 3) 8 ∙ 32 = 256 (кг) – зеленый виноград. 4) 144 + 256 = 400 (кг) – винограда всего
Ответ: 400 кг винограда всего.
Задача 2:

математика 4 класс Моро, Бантова - 1 часть страница 42. Год 2023. номер 191-4

1) 8 ∙ 32 = 256 (кг) – зеленого винограда. 2) 400 − 256 = 144 (кг) – черного винограда. 3) 144 : 9 = 16 (к.) – винограда
Ответ: 16 коробок с черным виноградом.

Номер 192.

Робот-пылесос на одной зарядке убирает 50 м² площади. Сколько раз надо зарядить робот-пылесос для уборки дома площадью 120 м²?

Ответ:

120 : 50 = 2 (ост. 20) – это значит робот-пылесос нужно зарядить 3 раза.
Ответ: 3 раза всего нужно зарядить робот-пылесос.

Номер 193.

Чем похожи, чем различаются уравнения каждой пары? В каком уравнении каждой пары неизвестное число больше? Сделай вывод. Проверь решением.

х + 37 = 78 х + 37 = 80
90 − х = 47 90 − х = 50
х − 28 = 32 х − 28 = 22
45 + х = 63 45 + х = 68

Ответ:

Номер 194.

Ответ:

1) 1 000 000 : 1 000 − 999 = 1 000 − 999 = 1 1 000 000 : 1 000 + 1 = 1 000 + 1 = 1 001 420 000 − 20 000 = 400 000 28 000 : 4 ∙ 100 = 7 000 ∙ 100 = 700 000
2)