Математика 3 класс учебник Моро, Волкова 2 часть ответы – страница 19

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2021-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 1.
Вычисли и проверь решение делением.
Ответ:
27 ∙ 3 = 81 32 ∙ 2 = 64
Проверка: Проверка:
81 : 3 = 27 64 : 2 = 32
27 = 27 32 = 32
17 ∙ 5 = 85 14 ∙ 6 = 84
Проверка: Проверка:
85 : 5 = 17 84 : 6 = 14
17 = 17 14 = 14
Вспомни зависимость между компонентами и результатом действия умножения и деления.
Вычислим.
27 ∙ 3 = (20 + 7) ∙ 3 = 20 ∙ 3 + 7 ∙ 3 = 60 + 21 = 81
Число 27 представим в виде суммы 20 и 7, и каждое слагаемое умножим на 3, а полученные числа сложим.
32 ∙ 2 = (30 + 2) ∙ 2 = 30 ∙ 2 + 2 ∙ 2 = 60 + 4 = 64
Число 32 представим в виде суммы 30 и 2, и каждое слагаемое умножим на 2, а полученные числа сложим.
17 ∙ 5 = (10 + 7) ∙ 5 = 10 ∙ 5 + 7 ∙ 5 = 50 + 35 = 85
Число 17 представим в виде суммы 10 и 7, и каждое слагаемое умножим на 5, а полученные числа сложим.
14 ∙ 6 = (10 + 4) ∙ 6 = 10 ∙ 6 +4 ∙ 6 = 60 + 24 = 84
Число 14 представим в виде суммы 10 и 4, и каждое слагаемое умножим на 6, а полученные числа сложим.
Сделаем проверку.
Умножение двух чисел можно проверить так:
Произведение делят на один множитель.
Должен получиться другой множитель.
Если этого не произойдёт, значит, в вычислениях
допущена ошибка.
Умножение двух чисел можно проверить так:
1) Произведение делят на один множитель.
2) Должен получиться другой множитель.
3) Если этого не произойдёт, значит, в вычислениях допущена ошибка.
27 ∙ 3 = 81
Проверка:
1) 81 : 3 = (60 + 21) : 3 = 20 + 7 = 27
2) 27 = 27
3) Вычисление выполнено верно
32 ∙ 2 = 64
Проверка:
1) 64 : 2 = (60 + 4) : 2 = 60 : 2 + 4 : 2 = 30 + 2 = 32
2) 32 = 32
3) Вычисление выполнено верно
17 ∙ 5 = 85
Проверка:
1) 85 : 5 = (50 + 35) : 5 = 10 + 7 = 17
2) 17 = 17
3) Вычисление выполнено верно
14 ∙ 6 = 84
Проверка:
1) 84 : 6 = (60 + 24) : 6 = 10 + 4 = 14
2) 14 = 14
3) Вычисление выполнено верно
Оформляем задание в тетрадь.
27 ∙ 3 = 81
Проверка:
1) 81 : 3 = 27
2) 27 = 27
32 ∙ 2 = 64
Проверка:
1) 64 : 2 = (60 + 4) : 2 = 60 : 2 + 4 : 2 = 30 + 2 = 32
2) 32 = 32
17 ∙ 5 = 85
Проверка:
1) 85 : 5 = 17
2) 17 = 17
14 ∙ 6 = 84
Проверка:
1) 84 : 6 = 14
2) 14 = 14
Номер 2.
Вычисли и проверь решение умножением.
Ответ:
84 : 3 = 28 72 : 2 = 36
Проверка: Проверка:
28 ∙ 3 = 84 36 ∙ 2 = 72
84 = 84 72 = 72
52 : 4 = 13 76 : 2 = 38
Проверка: Проверка:
13 ∙ 4 = 52 38 ∙ 2 = 76
52 = 52 76 = 76
Вспомни зависимость между компонентами и результатом действия умножения и деления.
Вычислим.
84 : 3 = (60 + 24) : 3 = 60 : 3 + 24 : 3 = 20 + 8 = 28
Число 84 представим в виде суммы 60 и 24, и каждое слагаемое разделим на 3, а полученные числа сложим.
72 : 2 = (60 + 12) : 2 = 60 : 2 + 12 : 2 = 30 + 6 = 36
Число 72 представим в виде суммы 60 и 12, и каждое слагаемое разделим на 2, а полученные числа сложим.
52 : 4 = (40 + 12) : 4 = 40 : 4 + 12 : 4 = 10 + 3 = 13
Число 52 представим в виде суммы 40 и 12, и каждое слагаемое разделим на 4, а полученные числа сложим.
76 : 2 = (60 + 16) : 2 = 60 : 2 + 16 : 2 = 30 + 8 = 38
Число 76 представим в виде суммы 60 и 16, и каждое слагаемое разделим на 2, а полученные числа сложим.
Сделаем проверку.
Деление можно проверить так:
Частное умножают на делитель и должно получиться делимое;
Если этого не произошло, значит, в вычислениях допущена ошибка.
84 : 3 = 28
Проверка:
1) 28 ∙ 3 = (20 + 8) ∙ 3 = 60 + 24 = 84
2) 84 = 84
3) Вычисление выполнено верно
72 : 2 = 36
Проверка:
1) 36 ∙ 2 = (30 + 6) ∙ 2 = 60 + 12 = 72
2) 72 = 72
3) Вычисление выполнено верно
52 : 4 = 13
Проверка:
1) 13 ∙ 4 = (10 + 3) ∙ 4 = 40 + 12 = 52
2) 52 = 52
3) Вычисление выполнено верно
76 : 2 = 38
Проверка:
1) 38 ∙ 2 = (30 + 8) ∙ 2 = 60 + 16 = 76
2) 76 = 76
3) Вычисление выполнено верно
Оформляем задание в тетрадь.
84 : 3 = 28
Проверка:
1) 28 ∙ 3 = 84
2) 84 = 84
72 : 2 = 36
Проверка:
1) 36 ∙ 2 = 72
2) 72 = 72
52 : 4 = 13
Проверка:
1) 13 ∙ 4 = 52
2) 52 = 52
76 : 2 = 38
Проверка:
1) 38 ∙ 2 = 76
2) 76 = 76
Номер 3.
Начерти три отрезка: длина первого отрезка 8 см, длина второго составляет одну четвертую длины первого, а длина третьего на 6 см больше длины второго.
Ответ:8 : 4 = 2 (см) – длина второго отрезка. 2 + 6 = 8 (см) – длина третьего отрезка.

1) Отрезок – геометрическая фигура, представляющая собой часть прямой, ограниченную с двух сторон точками.
2) Длина отрезка – расстояние между точками.
3) Доля – одна часть из тех, на которые разделили целое.
4) Первое слово в названии долей указывает на количество долей, которые взяли, а второе – на сколько частей разделили целое.
Оформляем условие в виде краткой записи.
.jpg)
Рассуждаем.
Длина первого отрезка 8 см. Длина второго – одна четвертая часть первого отрезка. Значит 8 см разделим на 4 части и возьмём только одну такую часть.
8 : 4 = 2 (см) – длина второго отрезка.
Продолжаем рассуждение.
Длина третьего отрезка на 6 см больше длины второго отрезка. Это значит, столько же, но плюс ещё 6 см.
2 + 6 = 8 (см) – длина третьего отрезка.
Начертим.
С помощью линейки начертим три отрезка длиной 8 см, 2 см и 8 см.
.jpg)
Номер 4.
Объясни решение уравнения и его проверку.

Чтобы найти неизвестный множитель х, надо произведение разделить на известный множитель 96 : 8 будет 12. Проверка: Вместо х представим 12 умножим 12 на 8 будет 96. 96 равно 96.
Уравнение – равенство, которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
Рассуждаем.
х ∙ 8 = 96
х – первый множитель
8 – второй множитель
96 – произведение
Чтобы найти один из множителей нужно произведение разделить на другой множитель.
х = 96 : 8 = 12
96 : 8 = (80 + 16 ) : 8 = 10 + 2 = 12
Ответ: 12.
Делаем проверку.
Чтобы произвести проверку нужно вместо х подставить найденный множитель. Должно получиться верное равенство. Если этого не произойдёт, значит, в вычислениях допущена ошибка.
х ∙ 8 = 96
Вместо х подставляем число 12, получим
12 ∙ 8 = (10 + 2) ∙ 8 = 80 + 16 = 96
96 = 96
Уравнение решено верно.
Номер 5.
Цена одной столовой ложки ☐ р., а чайной – ☐ р., купили по 3 тех и других ложек. Сколько рублей стоила покупка?
Подбери числа и реши задачу.
Цена одной столовой ложки 20 р., а чайной 10 р. Купили по 3 тех и других ложек. Сколько рублей стоила покупка?

1-й способ решения:
1) 20 · 3 = 60 (р.) – стоили столовые ложки.
2) 10 · 3 = 30 (р.) – заплатили за чайные ложки.
3) 60 + 30 = 90 (р.) – стоила покупка.
Ответ: 90 р. стоила покупка.
2-й способ решения:
1) 20 + 10 = 30 (р.) – стоят 1 столовая и 1 чайная ложка.
2) 30 · 3 = 90 (р.)
Ответ: 90 рублей стоит вся покупка.
Цена одной столовой ложки 21 р., а чайной 15 р. Купили по 3 тех и других ложек. Сколько рублей стоила покупка?
1-й способ решения:
1) 21 + 15 = 36 (р.) – стоимость столовой и чайной вместе.
2) 36 · 3 = 108 (р.) – вся покупка.
Ответ: 108 рублей.
2-й способ решения:
21 · 3 + 15 · 3 = 63 + 45 = 108 (р.) – вся покупка
или
(21 + 15) · 3 = 36 · 3 = 108 (р.) – вся покупка
Ответ: 108 рублей.
Данная задача: вида «цена, количество стоимость» характеризуется зависимостями между компонентами:
Цена ∙ количество = стоимость.
Стоимость: количество = цена.
Стоимость : цена = количество.
Дополняем условие недостающими данными.
Задача: Цена одной столовой ложки 21 р., а чайной – 15 р., купили по 3 тех и других ложек. Сколько рублей стоила покупка?
Оформляем условие в виде таблицы.
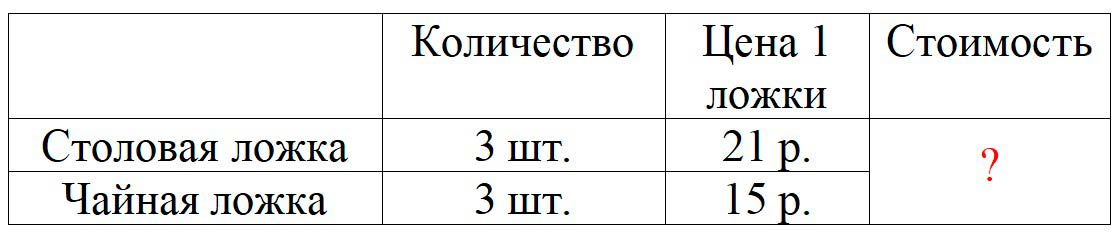
Рассуждаем.
Узнаем общую стоимость столовых ложек. Цена каждой ложки одинакова. Для этого нужно цену одной ложки умножить на количество ложек.
21 ∙ 3 = 63 (р.) – стоимость столовых ложек.
Продолжаем рассуждение.
Узнаем общую стоимость чайных ложек. Цена каждой ложки одинакова. Для этого нужно цену одной ложки умножить на количество ложек.
15 ∙ 3 = 45 (р.) – стоимость чайных ложек.
Продолжаем рассуждение.
Узнаем стоимость общей покупки. Общая покупка состоит из покупки столовый и чайных ложек. Чтобы узнать общую стоимость стоимости этих двух покупок нужно сложить.
63 + 45 = 108 (р.) – вся покупка.
Записываем ответ.
Ответ: 108 рублей.
Решение выражением:
21 ∙ 3 + 15 ∙ 3 = 108 (р.) –вся покупка, где 21 ∙ 3 – стоимость столовых ложек; 15 ∙ 3 – стоимость чайных ложек.
Рассуждаем.
Вычислим стоимость одного набора «столовая ложка + чайная ложка».
Набор состоит из двух частей, значит, чтобы узнать, сколько стоит набор, нужно сложить обе группы денег.
21 + 15 = 36 (р.) – стоимость столовой и чайной вместе.
Продолжаем рассуждение.
Вычислим сколько стоят 3 таких набора.
Нужно сложить стоимость трёх наборов. Но они одинаковы, значит
сложение одинаковых слагаемых можно заменить умножением.
36 ∙ 3 = 108 (р.) – вся покупка.
Записываем ответ.
Ответ: 108 рублей.
Решение выражением:
(21 + 15) ∙ 3 = 108 (р.) – вся покупка, где 21 + 15 – стоимость набора «столовая ложка + чайная ложка».
Номер 6.
Найди значения выражения c : d при с = 80, d = 4; с = 40, d = 2; с = 20, d = 1.
Ответ:с : d если с = 80, d = 4, то 80 : 4 = 20 с : d если с = 40, d = 2, то 40 : 2 = 20 с : d если с = 20, d = 1, то 20 : 1 = 20
1) с · d, значит, значение с нужно умножить на d.
2) Помни, что 10 = 1 дес.
Рассуждаем.
с : d, если
с = 80, d = 4, то 80 : 4 = 8 дес. : 4 = 2 дес. = 20
с : d, если
с = 40, d = 2, то 40 : 2 = 4 дес. : 2 = 2 дес. = 20
с : d, если
с = 20, d = 1, то 20 : 1 = 20
Если число разделить единицу, то получится это число.
Оформляем задание в тетрадь.
с : d, если
с = 80, d = 4, то 80 : 4 = 20
с : d, если
с = 40, d = 2, то 40 : 2 = 20
с : d, если
с = 20, d = 1, то 20 : 1 = 20
Номер 7.
Ответ:
1) Помни о порядке выполнения арифметических действий.
2) Сначала выполняются действия умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Вспомни, как найти деление методом подбора.
Расставляем порядок действий и выполняем вычисления.
Найдём частное методом подбора.
36 : 12 = ?
Пробуем в частном 2 и проверяем: 12 ∙ 2 = 24, 24 < 36, число 2 не подходит.
Пробуем в частном 3 и проверяем: 12 ∙ 3 = 36, 36 = 36, значит 36 : 12 = 3.
Ответ: 3.
36 : 18 = 2, так как 18 ∙ 2 = 36
Пробуем в частном 2 и проверяем: 18 ∙ 2 = 36, 36 = 36, значит 36 : 18 = 2.
Ответ: 2.
Вычислим значение выражения по действиям.
48 – 3 ∙ 7 = 27
В данном выражении присутствуют действия вычитание и умножение. Вначале выполняем действие умножение, а потом – вычитание.
1) 3 ∙ 7 = 21
2) 48 – 21 = 27
6 ∙ 9 – 38 = 16
В данном выражении присутствуют действия вычитание и умножение. Вначале выполняем действие умножение, а потом – вычитание.
1) 6 ∙ 9 = 54
2) 54 – 38 = 16
63 + 81 : 9 = 72
В данном выражении присутствуют действия сложение и деление. Вначале выполняем действие деление, а потом – сложение.
1) 81 : 9 = 9
2) 63 + 9 = 72
47 – 54 : 6 = 38
В данном выражении присутствуют действия вычитание и деление. Вначале выполняем действие деление, а потом – вычитание.
1) 54 : 6 = 9
2) 47 – 9 = 38
Оформляем задание в тетрадь.
36 : 12 = 3, так как 12 ∙ 3 = 36
36 : 18 = 2, так как 18 ∙ 2 = 36
48 – 3 ∙ 7 = 48 – 21 = 27
6 ∙ 9 – 38 = 54 – 38 = 16
63 + 81 : 9 = 63 + 9 = 72
47 – 54 : 6 = 47 – 9 = 38
Задание внизу страницы
Вычисли и выполни проверку.
Ответ:18 ∙ 4 = (10 + 8) ∙ 4 = 10 ∙ 4 + 8 ∙ 4 = 40 + 32 = 72
Проверка:
72 : 18 = 4
72 : 4 = 18
27 ∙ 3 = (20 + 7) ∙ 3 = 20 ∙ 3 + 7 ∙ 3 = 60 + 21 = 81
Проверка:
81 : 3 = 27
81 : 27 = 3
1) Помни, чтобы умножить сумму на число, можно вычислить сумму и умножить её на число.
2) Помни, чтобы умножить сумму на число, можно умножить на число каждое слагаемое и полученные результаты сложить.
Рассуждаем.
18 ∙ 4 = (10 + 8) ∙ 4 = 10 ∙ 4 + 8 ∙ 4 = 40 + 32 = 72
Представим число 18 в виде суммы чисел 10 и 8. Каждое слагаемое умножим на 4 и полученные числа сложим.
27 ∙ 3 = (20 + 7) ∙ 3 = 20 ∙ 3 + 7 ∙ 3 = 60 + 21 = 81
Представим число 27 в виде суммы чисел 20 и 7. Каждое слагаемое умножим на 3 и полученные числа сложим.
Сделаем проверку.
18 ∙ 4 = 72
Проверка:
1) 72 : 4 = (40 + 32) : 4 = 10 + 8 = 18
2) 18 = 18
3) Решено верно.
27 ∙ 3 = 81
Проверка:
1) 81 : 3 = (60 + 21) : 3 = 20 + 7 = 27
2) 27 = 27
3) Решено верно.
Оформляем задание в тетрадь.
18 ∙ 4 = 72
Проверка:
1) 72 : 4 = 18
2) 18 = 18
27 ∙ 3 = 81
Проверка:
1) 81 : 3 = 27
2) 27 = 27
Задание на полях страницы
Ребусы:



1) Вспомни зависимость между компонентами умножения и деления.
2) Внимательно рассмотри ряды выражений и подставь такие числа, чтобы равенства были верными.
Рассуждаем.
Вспомни таблиц умножения. Произведение каких двух чисел оканчивается на 1.
Варианты ответов:
3 ∙ 7 = 21 или 7 ∙ 3 = 21
9 ∙ 9 = 81
Вспомни таблиц умножения. На какое число нужно умножить число 8, чтобы произведение оканчивалось на 2.
Варианты ответов:
9 ∙ 8 = 72
4 ∙ 8 = 32
Вспомни таблицу умножения на 7. На какое число нужно умножить число 7, чтобы произведение оканчивалось на 2.
7 ∙ 6 = 42 или 6 ∙ 7 = 42
Вспомни таблиц умножения. Произведение каких двух чисел оканчивается на 7.
3 ∙ 9 = 27 или 9 ∙ 3 = 27
Оформляем задание в тетрадь.
Объясни решение уравнений и проверку.
Ответ:
х – неизвестный делитель. Чтобы найти неизвестный делитель, нужно делимое разделить на частное. Чтобы это проверить, подставляем вместо х полученное значение.

х – неизвестный множитель. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель. Чтобы это проверить, подставляем вместо х полученное значение.

х – неизвестное делимое. Чтобы найти неизвестное делимое, нужно делитель умножить на частное. Чтобы это проверить, подставляем вместо х полученное значение.
Уравнение – равенство, которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
Рассуждаем.
76 : х = 38
х – неизвестный делитель.
Чтобы найти делитель, нужно делимое разделить на частное.
Чтобы найти х, нужно 76 разделить на 38, получим:
х = 76 : 38
Пробуем в частном 2 и проверяем:
38 ∙ 2 = 76,
76 = 76, значит,
76 : 36 = 2.
х = 2
х ∙ 7 = 84
х – неизвестный множитель.
Чтобы найти один из множителей, нужно произведение разделить на другой множитель.
Чтобы найти х, нужно 84 разделить на 7, получим:
х = 84 : 7
84 : 7 = (70 + 14) : 7 = 70 : 7 + 14 : 7 = 10 + 2 = 12
Число 84 представим в виде суммы 70 и 14, и каждое слагаемое разделим на 7, а полученные числа сложим.
х = 12
х : 3 = 24
х – неизвестное делимое.
Чтобы найти делимое, нужно частное умножить на делимое.
Чтобы найти х, нужно 24 умножить на 3, получим:
х = 24 ∙ 3
24 ∙ 3 = (20 + 4) ∙ 3 = 20 ∙ 3 + 4 ∙ 3 = 60 + 12 = 72
Число 24 представим в виде суммы 20 и 4, и каждое слагаемое умножим на 3, а полученные числа сложим.
х = 72
Делаем проверку.
Чтобы произвести проверку, нужно вместо х подставить найденный множитель. Должно получиться верное равенство. Если этого не произойдёт, значит, в вычислениях допущена ошибка.
76 : х = 38
Проверка:
Вместо неизвестного х нужно подставить число 2.
76 : 2 = (60 + 16) : 2 = 60 : 2 + 16 : 2 = 30 + 8 = 38
38 = 38
х ∙ 7 = 84
Проверка: вместо неизвестного х нужно подставить число 12.
12 ∙ 7 = (10 + 2) ∙ 7 = 10 ∙ 7 + 2 ∙ 7 = 70 + 14 = 84
84 = 84
х : 3 = 24.
Проверка: вместо неизвестного х нужно подставить число 72.
72 : 3 = (60 + 12) : 3 = 60 : 3 + 12 : 3 = 20 + 4 = 24
24 = 24
Оформляем задание в тетрадь.
76 : х = 38
Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
х = 76 : 38
х = 2
Проверка: чтобы это проверить, подставляем вместо х полученное значение.
76 : 2 = 38
38 = 38
х ∙ 7 = 84
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
х = 84: 7
х = 12
Проверка: чтобы это проверить, подставляем вместо х полученное значение.
12 ∙ 7 = 84
84 = 84
х : 3 = 24
Чтобы найти неизвестное делимое, нужно делитель умножить на частное.
х = 24 ∙ 3
х = 72
Проверка: чтобы это проверить, подставляем вместо х полученное значение.
72 : 3 = 24
24 = 24
Номер 1.
Реши уравнения с объяснением.
Ответ:
Уравнение – равенство, которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
Рассуждаем.
18 ∙ х = 54
18 – первый множитель.
х – второй множитель.
54 – произведение.
Чтобы найти неизвестный множитель, нужно произведение разделить на другой множитель.
Чтобы найти х, нужно 54 разделить на 18.
х = 54 : 18
Пробуем в частном 3 и проверяем:
18 ∙ 3 = (10 + 8) ∙ 3 = 10 ∙ 3 + 8 ∙ 3 = 30 + 24 = 54
54 = 54, значит,
54 : 18 = 3
х = 3
х : 16 = 3
х – делимое.
16 – делитель.
3 – частное.
Чтобы найти делимое, нужно делитель умножить на частное.
Чтобы найти х, нужно 16 умножить на 3.
х = 16 ∙ 3
16 ∙ 3 = (10 + 6) ∙ 3 = 10 ∙ 3 + 6 ∙ 3 = 30 + 18 = 48
х = 48
57 : х = 3
57 – делимое.
х – делитель.
3 – частное.
Чтобы найти делитель, нужно делимое разделить на частное.
Чтобы найти, х нужно 57 разделить на 3.
х = 57 : 3
57 : 3 = (30 + 27) : 3 = 30 : 3 + 27 : 3 = 10 + 9 = 19
х = 19
Делаем проверку.
Чтобы произвести проверку нужно вместо х подставить найденный множитель. Должно получиться верное равенство. Если этого не произойдёт, значит, в вычислениях допущена ошибка.
18 ∙ х = 54
Проверка: вместо неизвестного х подставим число 3.
18 ∙ 3 = (10 + 8) ∙ 3 = 10 ∙ 3 + 8 ∙ 3 = 30 + 24 = 54
54 = 54
х : 16 = 3
Проверка: вместо неизвестного х подставим число 48.
48 : 16 = 3
Пробуем в частном 3 и проверяем:
16 ∙ 3 = (10 + 6) ∙ 3 = 10 ∙ 3 + 6 ∙ 3 = 30 + 18 = 48
48 = 48, значит,
48 : 16 = 3
3 = 3
57 : х = 3
Проверка: вместо неизвестного х подставим число 19.
57 : 19 = 3
Пробуем в частном 3 и проверяем:
19 ∙ 3 = (10 + 9) ∙ 3 = 10 ∙ 3 + 9 ∙ 3 = 30 + 27 = 57
57 = 57, значит,
57 : 19 = 3
3 = 3
Оформляем задание в тетрадь.
18 ∙ х = 54
Чтобы найти неизвестный множитель, нужно произведение разделить на другой множитель.
х = 54 : 18
х = 3
Проверка: чтобы это проверить, подставляем вместо х полученное значение.
18 ∙ 3 = 54
54 = 54
х : 16 = 3
Чтобы найти делимое, нужно делитель умножить на частное.
х = 16 ∙ 3
х = 48
Проверка: чтобы это проверить, подставляем вместо х полученное значение.
48 : 16 = 3
3 = 3
57 : х = 3
Чтобы найти делитель, нужно делимое разделить на частное.
х = 57 : 3
х = 19
Проверка: чтобы это проверить, подставляем вместо х полученное значение.
57 : 19 = 3
3 = 3
Номер 2.
Закончи выводы:
1) Чтобы найти неизвестный множитель, надо ... . 2) Чтобы найти неизвестное делимое, надо ... . 3) Чтобы найти неизвестный делитель, надо ... .
Ответ:1) ... произведение поделить на известный множитель. 2) ... частное умножить на делитель. 3) ... делимое поделить на частное.
Помни о зависимости между элементами и результатом действия умножения и деления.
Рассуждаем.
Вспомним зависимость между умножением и делением:
1 множитель · 2 множитель = произведение.
Произведение : 1 множитель = 2 множитель.
Произведение : 2 множитель = 1 множитель.
Делимое : делитель = частное.
Делимое : частное = делитель.
Частное · делитель = делимое.
Оформляем задание в тетрадь.
Закончим выводы.
1) Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
2) Чтобы найти неизвестное делимое, надо делитель умножить на частное.
3) Чтобы найди неизвестный делитель, надо делимое разделить на частное.
Номер 3.
Ответ:

1) a · b, значит, значение a нужно умножить на b.
2) c : k, значит, значение c нужно разделить на k.
Рассуждаем.
Представим данные выражения в виде уравнений.
17 ∙ х = 51
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
х = 51 : 17
Пробуем в частном 3 и проверяем:
17 ∙ 3 = (10 + 7) ∙ 3 = 10 ∙ 3 + 7 ∙ 3 = 30 + 21 = 51
51 = 51, значит,
51 : 17 = 3
х = 3
х ∙ 4 = 68
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
х = 68 : 4
68 : 4 = (40 + 28) : 4 = 40 : 4 + 28 : 4 = 10 + 7 = 17
х = 17
16 ∙ х = 96
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
х = 96 : 16
Пробуем в частном 6 и проверяем:
16 ∙ 6 = (10 + 6) ∙ 6 = 10 ∙ 6 + 6 ∙ 6 = 60 + 36 = 96
96 = 96, значит,
96 : 16 = 6
х = 6
64 : х = 4
Чтобы найди неизвестный делитель, надо делимое разделить на частное.
х = 64 : 4
64 : 4 = (40 + 24) : 4 = 40 : 4 + 24 : 4 = 10 + 6 = 16
х = 16
х : 6 = 13
Чтобы найти неизвестное делимое, надо делитель умножить на частное.
х = 13 ∙ 6
13 ∙ 6 = (10 + 3) ∙ 6 = 10 ∙ 6 + 3 ∙ 6 = 60 + 18 = 78
х = 78
80 : х = 5
Чтобы найди неизвестный делитель, надо делимое разделить на частное.
х = 80 : 5
80 : 5 = (50 + 30) : 5 = 50 : 5 + 30 : 5 = 10 + 6 = 16
х = 16
Оформляем задание в тетрадь.
Подставим полученные значения в таблицу.
.jpg)
Номер 4.
В туристский поход пошли 19 человек. На каждого взяли по 2 банки мясных консервов и по 3 банки овощных. Сколько всего банок с консервами взяли?
Ответ:
Можно оформить с помощью таблицы:

1-й способ решения:
1) 2 + 3 = 5 (б.) – консервов взяли.
2) 5 ∙ 19 = 95 (б.)
Ответ: 95 банок взяли всего.
2-й способ решения:
1) 2 ∙ 19 = 38 (б.) – мясных консервов взяли.
2) 3 ∙ 19 = 57 (б.) – овощных консервов взяли.
3) 38 + 57 = 95 (б.)
Ответ: 95 банок взяли всего.
Данная задача: вида «на 1 человека, кол-во человек, всего банок» характеризуется зависимостями между компонентами:
На 1 человека ∙ кол-во человек = всего банок.
Всего банок : на 1 человека = кол-во человек.
Всего банок : кол-во человек = на 1 человека.
Оформляем краткую запись.
-(2024).jpg)
Краткую запись можно оформить в виде таблицы:
-(2024).jpg)
Рассуждаем.
Узнаем сколько всего банок взяли на одного человека. Общее количество банок складывается из количества мясных и овощных банок. Значит, чтобы узнать, сколько всего взяли банок на одного человека, нужно сложить количество данных банок.
2 + 3 = 5 (б.) – консервов взяли на 1 человека.
Продолжаем рассуждение.
Мы знаем количество банок на одного человека и количество человек. Также известно, что на каждого человека взяли одинаковое количество банок. Чтобы узнать, сколько всего взяли банок, нужно количество человек умножить на количество банок на одного человека.
19 ∙ 5 = (10 + 9) ∙ 5 = 10 ∙ 5 + 9 ∙ 5 = 50 + 45 = 95 (б.) – консервов всего взяли.
Записываем ответ.
Ответ: 95 банок с консервами взяли.
Решение выражением: (2 + 3) ∙ 19 = 95 (б.), где 2 + 3 – количество банок на одного человека.
Рассуждаем.
Для каждого человека взяли одинаковое количество банок мясных консервов. Чтобы узнать, сколько всего взяли банок мясных консервов, нужно количество банок умножить на количество человек.
19 ∙ 2 = (10 + 9) ∙ 2 = 20 + 18 = 38 (б.) – мясных консервов взяли.
Продолжаем рассуждение.
Для каждого человека взяли одинаковое количество банок овощных консервов. Чтобы узнать сколько всего взяли банок овощных консервов, нужно количество банок умножить на количество человек.
19 ∙ 3 = (10 + 9) ∙ 3 = 30 +27 = 57 (б.) – овощных консервов взяли.
Продолжаем рассуждение.
Общее количество банок складывается из мясных и овощных консервов. Значит, чтобы узнать, сколько всего банок консервов взяли, нужно сложить количество банок мясных и овощных консервов.
38 + 57 = 95 (б.) – консервов всего взяли.
Записываем ответ.
Ответ: 95 банок с консервами взяли.
Решение выражением: 19 ∙ 2 + 19 ∙ 3 = 95 (б.), где 19 ∙ 2 – мясных консервов; 19 ∙ 3 – овощных консервов.
Номер 5.
Составь задачу по выражению (18 + 42) : 6.
Ответ:В ящики, каждый из которых вмещает по 6 кг разложили 18 кг мандарин и 42 кг апельсин. Сколько всего ящиков потребовалось?

(18 + 42) : 6 = 10 (ящ.)
Ответ: 10 ящиков потребовалось всего.
1) Чтобы разделить сумму на число можно вычислить сумму и разделить её на число;
2) Чтобы разделить сумму на число можно разделить на число каждое слагаемое и полученные результаты сложить.
Составляем задачу.
В ящики, каждый из которых вмещает по 6 кг разложили 18 кг мандарин и 42 кг апельсин. Сколько всего ящиков потребовалось?
Оформляем краткую запись в виде таблицы.
.jpg)
Рассуждаем.
Общее число фруктов складывается из количества мандарин и апельсин. Чтобы узнать, сколько всего фруктов разложили, нужно сложить количество мандарин и апельсин.
18 + 42 = 60 (кг) – всего фруктов разложили.
Продолжаем рассуждение.
В каждом ящике одинаковое количество фруктов. Чтобы узнать, сколько фруктов в каждом ящике, нужно общее количество фруктов разделить на количество ящиков.
60 : 6 = 10 (ящ.) – потребовалось.
Записываем ответ.
Ответ: 10 ящиков потребовалось.
Решение выражением: (18 + 42) : 6 = 10 (ящ.) – потребовалось, где 18 + 42 – всего фруктов.
Номер 6.
(Устно.) Назови числа от 7 до 70, которые делятся на 7 без остатка.
Ответ:7, 14, 21, 28, 35, 42, 49, 56, 63, 70.
Для выполнения задания обращайся к таблице умножения и деления на 7.
Рассуждаем.
Делятся на 7, значит, являются результатом таблицы умножения и деления 7.
7 ∙ 1 = 7
7 ∙ 2 = 14
7 ∙ 3 = 21
7 ∙ 4 = 28
7 ∙ 5 = 35
7 ∙ 6 = 42
7 ∙ 7 = 49
7 ∙ 8 = 56
7 ∙ 9 = 63
7 ∙ 10 = 70
Записываем ответ.
7, 14, 21, 28, 35, 42, 49, 56, 63, 70.
Номер 7.
Ответ:

1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем, действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Расставляем порядок действий и выполняем вычисления.
1 2
28 ∙ 3 − 57 = 27
1) 28 ∙ 3 = (20 + 8) ∙ 3 = 60 + 24 = 84
2) 84 – 57 = 27
2 1
34 + 13 ∙ 5 = 99
1) 13 ∙ 5 = (10 + 3) ∙ 5 = 50 + 15 = 65
2) 34 + 65 = 99
2 1 3
98 – 23 ∙ 4 + 24 = 30
1) 23 ∙ 4 = (20 + 3) ∙ 4 = 80 + 12 = 92
2) 98 – 92 = 6
3) 6 + 24 = 30
1 3 2
28 ∙ 2 – 13 ∙ 4 = 4
1) 28 ∙ 2 = (20 + 8) ∙ 2 = 40 + 16 = 56
2) 13 ∙ 4 = (10 + 3) ∙ 4 = 30 + 12 = 52
3) 56 – 52 = 4
(49 + 28) : 7 = 49 : 7 + 28 : 7 = 7 + 4 = 11
Каждое слагаемое разделим на 7 и полученные результаты сложим.
(64 + 24) : 4 = 88 : 4 = 22
1) 64 + 24 = 88
2) 88 : 4 = (80 + 8) : 4 = 20 + 2 = 22
Сложим слагаемые и полученную сумму разделим на 4.
Оформляем задание в тетрадь.
1 2
28 ∙ 3 − 57 = 84 − 57 = 27
2 1
34 + 13 ∙ 5 = 15 + 65 = 99
2 1 3
98 – 23 ∙ 4 + 24 = 98 – 92 + 24 = 6 + 24 = 30
1 3 2
28 ∙ 2 – 13 ∙ 4 = 56 – 52 = 4
(49 + 28) : 7 = 49 : 7 + 28 : 7 = 7 + 4 = 11
(64 + 24) : 4 = 88 : 4 = 22
Номер 8.
Узнай площадь каждого квадрата и закрашенной его части.

Площадь квадратов 2 ∙ 2 = 4 см2.
Первый квадрат разбит на 4 равные части, значит, площадь одной – 1 см2.
Второй квадрат разбит на 4 равные части, значит, площадь закрашенной – 3 см2.
Третий квадрат разбит на 4 равные части, значит, площадь закрашенной – 2 см2.
1) Чтобы вычислить площадь квадрата, нужно длину умножить на ширину.
2) Доля – одна часть из тех, на которые разделили целое.
3) Первое слово в названии долей указывает на количество долей, которые взяли, а второе – на сколько частей разделили целое.
Рассуждаем.
Все три квадрата равны.
Сторона каждого квадрата – 4 клетки = 2 см
2 см ∙ 2 см = 4 см2 – площадь каждого квадрата.
Продолжаем рассуждение.
Узнаем какая часть квадрата закрашена.
Квадрат 1. Фигура разделена на 4 равные части и закрашена одна из этих частей, значит закрашена одна четвертая часть.
Квадрат 2. Фигура разделена на 4 равные части и закрашено 3 из этих частей, значит закрашено три четвёртые части.
Квадрат 3. Фигура разделена на 4 равные части и закрашено 2 из этих частей, значит закрашено две четвёртые части.
Продолжаем рассуждение.
Узнаем площадь закрашенной части.
1) Чтобы найти площадь закрашенной части, нужно площадь квадрата разделить на 4 одинаковые части и взять одну такую часть:
4 см2 : 4 = 1 см2 – площадь голубой части.
2) Чтобы найти площадь закрашенной части нужно площадь квадрата разделить на 4 одинаковые части и взять три такие части:
4 см2 : 4 ∙ 3 = 1 см2 ∙ 3 = 3 см2 – площадь розовой части.
3) Чтобы найти площадь закрашенной части нужно площадь квадрата разделить на 4 одинаковые части и взять две такие части:
4 см2 : 4 ∙ 2 = 1 см2 ∙ 2 = 2 см2 – площадь желтой части.
Оформляем задание в тетрадь.
2 см ∙ 2 см = 4 см2 – площадь каждого квадрата.
4 см2 : 4 = 1 см2 – площадь голубой части.
4 см2 : 4 ∙ 3 = 3 см2 – площадь розовой части.
4 см2 : 4 ∙ 2 = 2 см2 – площадь желтой части.
Задание внизу страницы
Реши уравнения.
19 · х = 38 32 : х = 2
Ответ:19 · х = 38
х = 38 : 19
х = 2
Проверка:
19 · 2 = 38
38 = 38
Ответ: х = 2
32 : х = 2
х = 32 : 2
х = 16
Проверка:
32 : 16 = 2
2 = 2
Ответ: х = 16
Уравнение – равенство, которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
Рассуждаем.
19 ∙ х = 38
х – неизвестный множитель.
Чтобы найти неизвестный множитель, нужно значение произведения разделить на известный множитель.
32 : х = 2
х – неизвестный делитель.
Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
Решаем уравнение.
19 ∙ х = 38
х = 38 : 19
Пробуем в частном 2 и проверяем:
19 ∙ 2 = (10 + 9) ∙ 2 = 10 ∙ 2 + 9 ∙ 2 = 20 + 18 = 38
38 = 38, значит,
38 : 19 = 2
х = 2
32 : х = 2
х = 32 : 2
32 : 2 = (20 + 12) : 2 = 10 + 6 = 16
х = 16
Оформляем задание в тетрадь.
19 ∙ х = 38
х = 38 : 19
х = 2
Проверка:
19 ∙ 2 = 38
38 = 38
Ответ: х = 2
32 : х = 2
х = 32 : 2
х = 16
Проверка:
32 : 16 = 2
2 = 2
Ответ: х = 16
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.