Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 46

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2023.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 1.
За 5 дней в семье израсходовали 10 кг овощей. Сколько овощей израсходовали за 3 дня, если каждый день расходовали овощей поровну?

1-й способ решения: 1) 10 : 5 = 2 (кг) – овощей, за один день. 2) 2 ∙ 3 = 6 (кг) – овощей, за три дня. Ответ: 6 кг овощей расходовали каждый день.
2-й способ решения: 10 : 5 ∙ 3 = 2 ∙ 3 = 6 (кг) – израсходовали за 3 дня. Ответ: 6 кг.
Данная задача: вида «расход в 1 день, количество дней, общий расход» характеризуется зависимостями между компонентами:
Расход в 1 день · количество дней = общий расход.
Общий расход : расход в 1 день = количество дней.
Общий расход : количество дней = расход в 1 день.
Оформляем условие в виде таблицы.
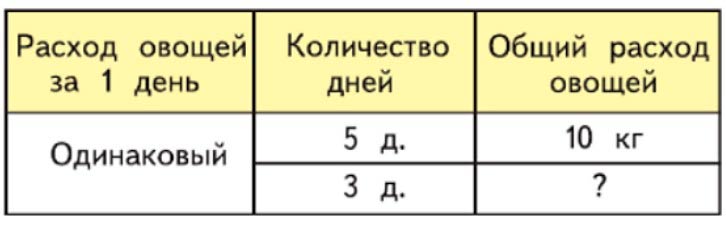
Рассуждаем.
За 5 дней в семье израсходовали 10 кг овощей, но неизвестно, сколько кг овощей расходовали в каждый из дней. При этом, расход в каждый день одинаковый. Поэтому, чтобы узнать, сколько овощей расходовали за 1 день, нужно общий расход овощей разделить на количество дней.
10 : 5 = 2 (кг) – овощей, за один день.
Продолжаем рассуждение.
В первом действии мы узнали расход овощей в 1 день. Теперь, зная расход и количество дней, нужно узнать общий расход овощей. Значит, чтобы узнать каков общий расход овощей, нужно сложить расход овощей в каждый из 3 дней.
Но расход овощей в каждый из дней одинаковый, поэтому сложение одинаковых слагаемых можно заменить умножением.
2 · 3 = 6 (кг) – овощей за три дня.
Записываем ответ.
Ответ: 6 кг овощей.
Решение выражением:
10 : 5 ∙ 3 = 6 (кг)
Номер 2.
За 6 м ленты заплатили 18 р. Сколько рублей стоит 9 м такой ленты?
Ответ:
1-й способ решения: 1) 18 : 6 = 3 (руб.) – стоит 1 м ленты. 2) 3 ∙ 9 = 27 (руб.) Ответ: 27 рублей стоит 9 м ленты.
2-й способ решения: 18 : 6 ∙ 9 = 3 ∙ 9 = 27 (руб.) – стоит 9 метров. Ответ: 27 рублей.
Данная задача: вида «цена, количество, стоимость» характеризуется зависимостями между компонентами:
Цена · количество = стоимость.
Стоимость : цена = количество.
Стоимость : количество = цена.
Оформляем условие в виде таблицы.
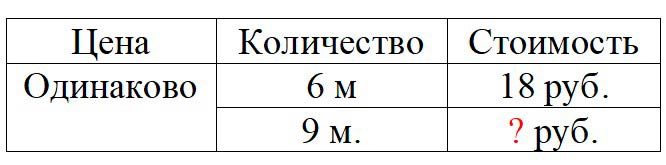
Рассуждаем.
За 6 метров ленты заплатили 18 рублей. Соответственно, неизвестна цена одного метра ленты.
При этом цена метра ленты одинаковая, и что чтобы узнать цену метра ленты, нужно стоимость всех метров ленты разделить на количество купленной ленты.
18 : 6 = 3 (руб.) – стоимость 1 метра ленты.
Продолжаем рассуждение.
Теперь мы знаем цену одного метра ленты. Количество купленной ленты – 9 метров.
Неизвестна общая стоимость ленты. Чтобы узнать, сколько стоит лента, нужно сложить стоимости каждого купленного метра ленты.
Но цена ленты при этом одинаковая, значит, что за каждый метр ленты заплатили равное количество денег. Соответственно, сложение одинаковых слагаемых можно заменить умножением.
3 · 9 = 27 (руб.) – стоимость 9 метров ленты.
Записываем ответ.
Ответ: 27 рублей.
Решение выражением:
18 : 6 ∙ 9 = 27 (руб.).
Номер 3.
Ответ:54 : 6 = 9 9 : 3 = 3 42 : 6 = 7 16 : 4 = 4 36 : 9 = 4 25 : 5 = 5 40 : 8 = 5 36 : 6 = 6

1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
4) Для выполнения задания обращайся к таблице умножения и деления с числом 2, 3,4, 5, 6.
Выполним деление.
54 : 6 = 9
Вспомним таблицу умножения на 6. При умножении какого числа на 6 получится 54? Это число 9, так как 6 · 9 = 54.
42 : 6 = 7
Вспомним таблицу умножения на 6. При умножении какого числа на 6 получится 42? Это число 7, так как 6 · 7 = 42.
36 : 9 = 4
Вспомним таблицу умножения. При умножении какого числа на 9 получится 36? Это число 4, так как 4 · 9 = 36.
40 : 8 = 5
Вспомним таблицу умножения. При умножении какого числа на 8 получится 40? Это число 5, так как 5 · 8 = 40.
Выполним вычисления по действиям.
Расставим порядок действий и вычислим.
Так как в данных выражениях присутствуют скоби, поэтому первым действием выполняем действие в скобках, па потом действие вне скобок.
1 2
(52 − 31) : 3 = 7
1) 52 − 31 = (50 − 20) + (2 − 1) = 20 + 1 = 21
2) 21 : 3 = 7,так как 3 · 7 = 21
2 1
54 : (16 − 7) = 6
1) 16 – 7 = 16 – (6 + 1) = (16 – 6) – 1 = 10 – 1 = 9
2) 54 : 9 = 6, так как 6 · 9 = 54
1 2
(12 + 18) : 6 = 5
1) 12 + 18 = (10 + 10) + (2 + 8) = 20 + 10 = 30
2) 30 : 6 = 5, так как 6 · 5 = 30
2 1
35 : (30 – 23) = 5
1) 30 – 23 = (20 + 10) – (20 + 3) = (20 – 20) + (10 – 3) = 7
2) 35 : 7 = 5, так как 5 · 7 = 35
Выполним деление.
9 : 3 = 3
Вспомним таблицу умножения на 3. При умножении какого числа на 3 получится 9? Это число 3, так как 3 · 3 = 9.
16 : 4 = 4
Вспомним таблицу умножения на 4. При умножении какого числа на 4 получится 16? Это число 4, так как 4 · 4 = 16.
25 : 5 = 5
Вспомним таблицу умножения на 5. При умножении какого числа на 5 получится 25? Это число 5, так как 5 · 5 = 25.
36 : 6 = 6
Вспомним таблицу умножения на 6. При умножении какого числа на 6 получится 36? Это число 6, так как 6 · 6 = 36.
Выполним вычисления по действиям.
Расставим порядок действий и вычислим.
В данных выражениях присутствуют действия умножение и деление – они равносильны, поэтому выполняем действия по порядку слева направо.
1 2
6 ∙ 5 : 10 = 3
1) 6 · 5 = 30
2) 30 : 10 = 3, так как 3 · 10 = 30
1 2
3 · 8 : 6 = 4
1) 3 · 8 = 24
2) 24 : 6 = 4, так как 6 · 4 = 24
1 2
5 · 7 : 5 = 7
1) 5 · 7 = 35
2) 35 : 5 = 7
1 2
5 · 4 : 10 = 2
1) 5 · 4 = 20
2) 20 : 10 = 2, так как 2 · 10 = 20
Оформим задание в тетрадь.
54 : 6 = 9
42 : 6 = 7
36 : 9 = 4
40 : 8 = 5
(52 − 31) : 3 = 21 : 3 = 7
54 : (16 − 7) = 54 : 9 = 6
(12 + 18) : 6 = 30 : 6 = 5
35 : (30 − 23) = 35 : 7 = 5
9 : 3 = 3
16 : 4 = 4
25 : 5 = 5
36 : 6 = 6
6 ∙ 5 : 10 = 30 : 10 = 3
3 ∙ 8 : 6 = 24 : 6 = 4
5 ∙ 7 : 5 = 35 : 5 = 7
5 ∙ 4 : 10 = 20 : 10 = 2
Номер 4.
Ответ:
1) b · 6, значит, увеличить число b в 6 раз, вычисляется умножением.
2) Вспомни, переместительное свойство умножения – а · b = b · a – от перестановки мест слагаемых, произведение не изменяется.
Промежуточные вычисления.
При вычислении значении буквенного выражения нужно вместо неизвестной буквы подставить заданное число.
b · 6
При b = 1, 1 · 6 = 6
где 1 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
При b = 2, 2 · 6 = 12
где 2 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
При b = 3, 3 · 6 = 18
где 3 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
При b = 4, 4 · 6 = 24
где 4 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
При b = 5, 5 · 6 = 30
где 5 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
При b = 6, 6 · 6 = 36
где 6 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
При b = 7, 7 · 6 = 6 · 7 = 42
где 6 – это одинаковое слагаемое, а 7– количество одинаковых слагаемых.
Применяем переместительное свойство умножения.
При b = 8, 8 · 6 = 6 · 8 = 48
где 6 – это одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
Применяем переместительное свойство умножения.
При b = 9, 9 · 6 = 6 · 9
где 6 – это одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
Применяем переместительное свойство умножения.
Заполним таблицу.
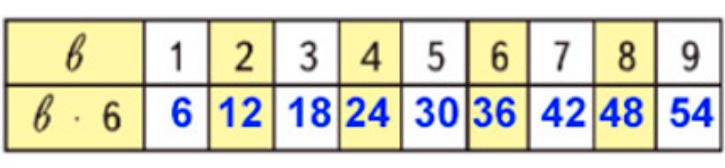
Номер 5.
С первого поля вывезли 16 стогов сена, а со второго – на 8 стогов больше, чем с первого. Сколько стогов сена вывезли с этих двух полей?
Ответ:

1-й способ решения:
1) 16 + 8 = 24 (ст.) – сена вывезли со второго поля.
2) 16 + 24 = 40 (ст.)
Ответ: 40 стогов сена вывезли с двух полей.
2-й способ решения: 16 + (16 + 8) = 16 + 24 = 40 (ст.) – вывезли с двух полей. Ответ: 40 стогов сена.
1) «на 8 стогов больше», значит, вычисляется сложением, знак плюс.
2) «всего», значит, вычисляется сложением, знак плюс.
Оформляем условие в виде краткой записи.
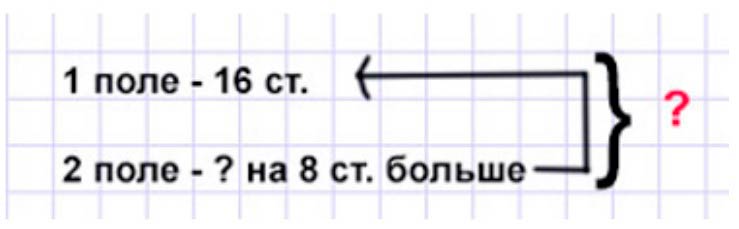
Рассуждаем.
С первого поля вывезли 16 стогов сена, а со второго – на 8 стогов больше. Значит, со второго поля вывезли столько стогов, сколько с первого и еще 8 стогов. Соответственно, чтобы узнать, сколько стогов сена было на втором поле, нужно к количеству стогов первого прибавить 8 стогов.
16 + 8 = 24 (ст.) – сена вывезли со второго поля.
Продолжаем рассуждение.
Общее количество стогов сена на полях складывается из количества сена первого и второго поля. Значит, чтобы узнать, сколько стогов сена было всего, нужно сложить количество сена обоих стогов.
16 + 24 = 40 (ст.) – сена вывезли с двух полей.
Записываем ответ.
Ответ: 40 стогов сена.
Решение выражением:
16 + (16 + 8) = 40 (ст.)
Задание внизу страницы
6 одинаковых игрушечных машинок стоят 48 р. Сколько рублей стоят 5 таких машинок?
Ответ:
1-й способ решения: 1) 48 : 6 = 8 (р.) – цена 1 машинки. 2) 8 ∙ 5 = 40 (р.) Ответ: 5 машинок стоят 40 рублей.
2-й способ решения: 48 : 6 ∙ 5 = 8 ∙ 5 = 40 (руб.) – стоят 5 машинок. Ответ: 40 рублей.
Данная задача: вида «цена, количество, стоимость» характеризуется зависимостями между компонентами:
Цена · количество = стоимость.
Стоимость : цена = количество.
Стоимость : количество = цена.
Оформляем условие в виде таблицы.

Рассуждаем.
6 одинаковых игрушечных машинок стоит 48 рублей. Соответственно, неизвестна цена одной машинки.
При этом цена машинок одинаковая, и что чтобы узнать цену машинки, нужно стоимость машинок разделить на количество.
48 : 6 = 8 (руб.) – цена одной машинки.
Продолжаем рассуждение.
Теперь нам известна цена машинки. Количество машинок – 5 штук.
Нам неизвестная общая стоимость всех машинок. Она складывается из цен всех 5 машинок. Значит, чтобы узнать, сколько стоят все машинки, нужно стоимости машинок сложить.
Но цена машинок одинаковая, т.е, каждая стоит равное количество денег. Поэтому сложением одинаковых слагаемых можно заменить умножением.
8 · 5 = 40 (руб.) – цена 5 машинок.
Записываем ответ.
Ответ: 40 рублей.
Решение выражением:
48 : 6 ∙ 5 = 40 (руб.).
Задание на полях страницы
Какое выражение лишнее?

Ответ:
Лишнее выражение 7 ∙ 6 так как это пример на умножение, а все прочие на деление.
Чтобы понять, какое выражение лишнее, нужно рассмотреть их и сравнить: из каких компонентов состоит, на каких арифметических действиях основаны, каковы их значения.
Вычислим выражения.
Опишем все выражения, вычислим их значения.
48 : 6 = 8,
так как 6 · 8 = 48,
где 6 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
12 : 6 = 2,
так как 6 · 2 = 12,
где 6 – одинаковое слагаемое, а 2 – количество одинаковых слагаемых.
24 : 6 = 4,
так как 6 · 4 = 24,
где 6 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.
6 : 6 = 1, так как 6 · 1 = 6, где 6 – одинаковое слагаемое, а 1 – количество одинаковых слагаемых.
54 : 6 = 9,
так как 6 · 9 = 54,
где 6 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
42 : 7 = 6,
так как 6 · 7 = 42,
где 6 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
7 · 6 = 6 · 7 = 42
Применяем переместительное свойство умножения,
где 6 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
Делаем вывод.
Получается, что лишним может быть выражение: 7 · 6, потому что это единственное выражение, основанное на арифметическом действии умножения.
Ответ: 7 · 6 – лишнее выражение.
Номер 1.
12 + 38 - 33 8 ∙ 3 : 6
55 - (20 + 8) 3 ∙ (8 : 2)
42 - 16 - 20 36 : 9 ∙ 7
(48 - 16) : 8 3 ∙ 4 : 6
14 + 35 : 7 9 ∙ 2 : 3
6 ∙ (20 - 16) 6 ∙ 4 : 8

1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Рассуждаем.
12 + 38 – 33
В данном выражении присутствуют действия сложение и вычитание – они равносильны, поэтому выполняем действия по порядку слева направо.
55 – (20 + 8)
В данном выражении присутствуют действия сложение и вычитание, а также скобки. Поэтому вначале выполняем действие в скобках – сложение, а потом вне скобок – вычитание.
42 – 16 – 20
В данном выражении присутствуют действия вычитание, поэтому выполняем действия по порядку слева направо.
8 · 3 : 6
В данном выражении присутствуют действия умножение и деление – они равносильны, поэтому выполняем действия по порядку слева направо.
3 · (8 : 2)
В данном выражении присутствуют действия умножение и деление, а также скобки. Поэтому вначале выполняем действие в скобках – деление, а потом вне скобок – умножение.
36 : 9 · 7
В данном выражении присутствуют действия умножение и деление – они равносильны, поэтому выполняем действия по порядку слева направо.
(48 – 16) : 8
В данном выражении присутствуют действия вычитание и деление, а также скобки. Поэтому вначале выполняем действие в скобках – вычитание, а потом вне скобок – деление.
14 + 35 : 7
В данном выражении присутствуют действия сложение и деление. Вначале выполняем действие деление, а потом сложение.
6 · (20 – 16)
В данном выражении присутствуют действия вычитание и умножение, а также скобки. Поэтому вначале выполняем действие в скобках – вычитание, а потом вне скобок – умножение.
3 · 4 : 6
В данном выражении присутствуют действия умножение и деление – они равносильны, поэтому выполняем действия по порядку слева направо.
9 · 2 : 3
В данном выражении присутствуют действия умножение и деление – они равносильны, поэтому выполняем действия по порядку слева направо.
6 · 4 : 8
В данном выражении присутствуют действия умножение и деление – они равносильны, поэтому выполняем действия по порядку слева направо.
Расставим действия и вычислим по действиям.
1 2
12 + 38 − 33 = 17
1) 12 + 38 = 50
2) 50 − 33 = 17
2 1
55 − (20 + 8) = 27
1) 20 + 8 = 28
2) 55 − 28 = 27
1 2
42 − 16 − 20 = 6
1) 42 – 16 = 26
2) 26 − 20 = 6
1 2
8 · 3 : 6 = 4
1) 8 ∙ 3 = 24
2) 24 : 6 = 4
2 1
3 ∙ (8 : 2) = 12
1) 8 : 2 = 4
2) 3 ∙ 4 = 12
1 2
36 : 9 ∙ 7 = 28
1) 36 : 9 = 4
2) 4 ∙ 7 = 28
1 2
(48 − 16) : 8 = 4
1) 48 – 16 = 32
2) 32 : 8 = 4
2 1
14 + 35 : 7 = 19
1) 35 : 7 = 5
2) 14 + 5 = 19
2 1
6 ∙ (20 − 16) = 24
1) 20 – 16 = 4
2) 6 ∙ 4 = 24
1 2
3 ∙ 4 : 6 = 2
1) 3 ∙ 4 = 12
2) 12 : 6 = 2
1 2
9 ∙ 2 : 3 = 6
1) 9 ∙ 2 = 18
2) 18 : 3 = 6
1 2
6 ∙ 4 : 8 = 3
1) 6 ∙ 4 = 24
2) 24 : 8 = 3
Оформим задание в тетрадь.
12 + 38 − 33 = 50 – 33 = 17
55 − (20 + 8) = 55 – 28 = 27
42 − 16 − 20 = 26 – 20 = 6
8 ∙ 3 : 6 = 24 : 6 = 4
3 ∙ (8 : 2) = 3 · 4 = 12
36 : 9 ∙ 7 = 4 · 7 = 28
(48 − 16) : 8 = 32 : 8 = 4
14 + 35 : 7 = 14 + 5 = 19
6 ∙ (20 − 16) = 6 · 4 = 24
3 ∙ 4 : 6 = 12 : 6 = 2
9 ∙ 2 : 3 = 18 : 3 = 6
6 ∙ 4 : 8 = 14 : 8 = 3
Номер 2.
Расставь скобки так, чтобы равенства стали верными.
31 - 10 - 3 = 24 54 - 12 + 8 = 34
Ответ:
1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
Расставим скобки и порядок действий.
2 1
31 − (10 − 3) = 24
2 1
54 − (12 + 8) = 34
Шаг 2 Сделаем проверку и вычисления по действиям.
31 − (10 − 3) = 24
1) 10 – 3 = 7
2) 31 − 7 = 24
54 − (12 + 8) = 34
1) 12 + 8 = 20
2) 54 − 20 = 34
Оформим задание в тетрадь.
31 − (10 − 3) = 31 – 7 = 24
54 − (12 + 8) = 54 – 20 = 34
Номер 3.
3 ◯ 6 ◯ 2 = 9 9 ◯ 3 ◯ 6 = 18
7 ◯ 3 ◯ 9 = 30 2 ◯ 8 ◯ 9 = 7

Производи разные действия с числами, меняй знаки арифметических действий, пока не придешь к верному решению.
Расставим знаки арифметических действий.
3 · 6 : 2 = 9
Первым действием поставим знак умножение, а вторым – деление.
7 · 3 + 9 = 30
Первым действием поставим знак умножение, а вторым – сложение.
9 + 3 + 6 = 18
Поставим первым и вторым действием знаки сложения.
2 · 8 – 9 = 7
Первым действием поставим знак умножение, а вторым – вычитание.
Выполняем проверку, вычислив по действиям.
1 2
3 · 6 : 2 = 9
1) 3 ∙ 6 = 18
2) 18 : 2 = 9
1 2
7 ∙ 3 + 9 = 30
1) 7 ∙ 3 = 21
2) 21 + 9 = 30
1 2
9 + 3 + 6 = 18
1) 9 + 3 = 12
2) 12 + 6 = 18
1 2
2 ∙ 8 − 9 = 7
1) 2 ∙ 8 = 18
2) 18 – 9 = 7
Оформляем задание в тетрадь.
3 ∙ 6 : 2 = 18 : 2 = 9
7 ∙ 3 + 9 = 21 + 9 = 30
9 + 3 + 6 = 12 + 6 = 18
2 ∙ 8 − 9 = 18 – 9 = 7
Номер 4.

Увеличь в 7 раз
8 ∙ 7 = 56
6 ∙ 7 = 42
9 ∙ 7 = 63
4 ∙ 7 = 28
3 ∙ 7 = 21
1 ∙ 7 = 7
Уменьши в 6 раз
42 : 6 = 7
30 : 6 = 5
54 : 6 = 9
36 : 6 = 6
18 : 6 = 36 : 6 = 1
1) Увеличь в 7 раз, значит, умножь на 7, вычисляется умножением.
2) Уменьши в 6 раз, значит, раздели на 6, вычисляется делением.
Выполняем вычисления с пояснениями.
Увеличь в 7 раз – это значит данное число умножить на 7.
8 · 7 = 7 · 8 = 56,
где 7 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
Применяем переместительный закон умножения.
6 · 7 = 42,
где 6 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
9 · 7 = 7 · 9 = 63,
где 7 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
Применяем переместительный закон умножения.
4 · 7 = 28,
где 4 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
3 · 7 = 21,
где 3 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
1 · 7 = 7,
где 1 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
Уменьши в 6 раз – это значит данное число разделить на 6.
42 : 6 = 7,
так как 6 · 7 = 42,
где 6 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
30 : 6 = 5,
так как 6 · 5 = 30,
где 6 – одинаковое слагаемое, а 5 – количество одинаковых слагаемых.
54 : 6 = 9,
так как 6 · 9 = 54,
где 6 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
36 : 6 = 6,
так как 6 · 6 = 36,
где 6 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
18 : 6 = 3,
так как 6 · 3 = 18,
где 6 – одинаковое слагаемое, а 3 – количество одинаковых слагаемых.
6 : 6 = 1,
так как 6 · 1 = 6,
где 6 – одинаковое слагаемое, а 1 – количество одинаковых слагаемых.
Оформляем задание в тетрадь.
Увечить в 7 раз:
8 ∙ 7 = 56
6 ∙ 7 = 42
9 ∙ 7 = 63
4 ∙ 7 = 28
3 ∙ 7 = 21
1 ∙ 7 = 7
Уменьши в 6 раз:
42 : 6 = 7
30 : 6 = 5
54 : 6 = 9
36 : 6 = 6
18 : 6 = 3
6 : 6 = 1
Номер 5.

Увеличь на 7
14 + 7 = 21
35 + 7 = 42
63 + 7 = 70
56 + 7 = 63
42 + 7 = 49
21 + 7 = 28
Уменьши на 6
30 - 6 = 24
12 - 6 = 6
24 - 6 = 18
42 - 6 = 36
6 - 6 = 0
18 - 6 = 12
1) Увеличь на 7, значит, прибавить 7, вычисляется сложением.
2) Уменьши на 6, значит, вычти 6, вычисляется вычитанием.
Выполняем вычисления с пояснениями.
Увеличь на 7 – это значит к данному числу прибавить число 7.
14 + 7 = 14 + (6 + 1) = (14 + 6) + 1 = 20 + 1 = 21
Число 7 разложим на сумму чисел 6 и 1. Вначале к числу 14 прибавим число 6, а потом прибавим число 1.
35 + 7 = 35 + (5 + 2) = (35 + 5) + 2 = 40 + 2 = 42
Число 7 разложим на сумму чисел 5 и 2. Вначале к числу 35 прибавим число 5, а потом прибавим число 2.
63 + 7 = (60 + 3) + 7 = 60 + (3 + 7) + 60 + 10 = 70
Сложим по разрядам: вначале сложим единицы, а потом десятки.
56 + 7 = 56 + (4 + 3) = (56 + 4) + 3 = 60 + 3 = 63
Число 7 разложим на сумму чисел 4 и 3. Вначале к числу 56 прибавим число 4, а потом прибавим число 3.
42 + 7 = (40 + 2) + 7 = 40 + (2 + 7) = 40 + 9 = 49
Сложим по разрядам: вначале сложим единицы, а потом десятки.
21 + 7 = (20 + 1) + 7 = 20 + (1 + 7) = 20 + 8 = 28
Сложим по разрядам: вначале сложим единицы, а потом десятки.
Уменьши на 6 – это значит из данного числа вычесть число 6.
30 – 6 = (20 + 10) – 6 = 20 + (10 – 6) = 20 + 4 = 24
Вычитаем единицы. От числа 0 мы не можем отнять 6.
Занимаем 1 дес. = 10 ед., 10 – 6 = 4 – получилось единиц.
Записываем в разряде единиц число 4.
Вычитаем десятки. Было 3 дес., мы занимали 1 дес, осталось 3 – 1 = 2 дес.,
Записываем в разряде десятков число 2.
Читаем ответ: 24.
12 – 6 = 12 – (2 + 4) = (12 – 2) – 4 = 10 – 4 = 6
Число 6 разложим на сумму чисел 2 и 4. Из числа 12 вначале вычтем число 2, а потом вычтем число 4.
24 – 6 = 24 – (4 + 2) = (24 – 4) – 2 = 20 – 2 = 18
Число 6 разложим на сумму чисел 4 и 2. Из числа 24 вычтем сначала число 4, а потом вычтем число 2.
42 – 6 = 42 – (2 + 4) = (42 – 2) – 4 = 40 – 4 = 36
Число 6 разложим на сумму чисел 2 и 4. Из числа 42 вначале вычтем число 2, а потом вычтем число 4.
6 – 6 = 0
Если из числа вычесть само число, то получится нуль.
18 – 6 = (10 + 8) – 6 = 10 + (8 – 6) = 10 + 2 = 12
Вычитаем единицы из единиц, а десятки из десяток.
Оформляем задание в тетрадь.
Увеличь на 7:
14 + 7 = 21
35 + 7 = 42
63 + 7 = 70
56 + 7 = 63
42 + 7 = 49
21 + 7 = 28
Уменьши на 6:
30 − 6 = 24
12 − 6 = 6
24 − 6 = 18
42 − 6 = 36
6 − 6 = 0
18 − 6 = 12
Номер 6.
5 ∙ 9 36 : 4
9 ∙ 3 28 : 7
4 ∙ 9 21 : 3
8 ∙ 4 - 18 : 6 47 + 4 ∙ 3 - 18
32 : 4 + 3 ∙ 4 51 - 32 + 6 ∙ 3
24 : 3 - 2 ∙ 4 27 : 9 + 29 - 7
5 ∙ 9 = 45 36 : 4 = 9
9 ∙ 3 = 27 28 : 7 = 4
4 ∙ 9 = 36 21 : 3 = 7

1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
4) Для выполнения задания обращайся к таблице умножения и деления с числом 2, 3,4, 5, 6, 7.
Выполним умножение.
5 · 9 = 45,
где 5 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
9 · 3 = 3 · 9 = 27,
где 3 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
Применяем переместительный закон умножения.
4 · 9 = 36,
где 4 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
Выполним деление.
36 : 4 = 9,
так как 4 · 9 = 36,
где 4 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
28 : 7 = 4,
так как 7 · 4 = 28,
где 7 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.
21 : 3 = 7,
так как 3 · 7 = 21,
где 3 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
Выполним вычисления по действиям.
1 3 2
8 · 4 − 18 : 6 = 29
1) 8 · 4 = 32
2) 18 : 6 = 3
3) 32 − 3 = 29
1 3 2
32 : 4 + 3 · 4 = 20
1) 32 : 4 = 8
2) 3 ∙ 4 = 12
3) 8 + 12 = (8 + 2) + 10 = 10 + 10 = 20
1 3 2
24 : 3 − 2 ∙ 4 = 0
1) 24 : 3 = 8
2) 2 ∙ 4 = 8
3) 8 − 8 = 0
2 1 3
47 + 4 ∙ 3 − 18 = 41
1) 4 ∙ 3 = 12
2) 47 + 12 = 59
3) 59 − 18 = (50 – 10) + (9 – 8) = 40 + 1 = 41
2 3 1
51 − 32 + 6 ∙ 3 = 37
1) 6 ∙ 3 = 18
2) 51 − 32 = 19
3) 19 + 18 = 19 + (1 + 17) = (19 + 1) + 17 = 20 + 17 = 37
1 3 2
27 : 9 + 29 − 7 = 25
1) 27 : 9 = 3
2) 3 + 29 = (1 + 2) + 29 = 2 + (29 + 1) = 2 + 30 = 32
3) 32 − 7 = 32 – (2 + 5) = (32 – 2) – 5 = 30 – 5 = 25
Оформим задание в тетрадь.
5 ∙ 9 = 45
9 ∙ 3 = 27
4 ∙ 9 = 36
36 : 4 = 9
28 : 7 = 4
21 : 3 = 7
8 ∙ 4 − 18 : 6 = 32 – 3 = 29
32 : 4 + 3 ∙ 4 = 8 + 12 = 20
24 : 3 − 2 ∙ 4 = 8 – 8 = 0
47 + 4 ∙ 3 − 18 = 47 + 12 – 18 = 59 –18 = 41
51 − 32 + 6 ∙ 3 = 51 – 32 + 18 = 19 + 18 = 37
27 : 9 + 29 − 7 = 3 + 29 – 7 = 32 – 7 = 25
Номер 7.
В зале музея выставили 20 картин, из них 6 портретов, остальные − пейзажи. На сколько больше выставили пейзажей, чем портретов?
Начерти, какой может быть тень на стене от картины с семейным портретом.

1) 20 - 6 = 14 (к.) – выставили в галерее.
2) 14 - 6 = 8 (к.)
Ответ: пейзажей на 8 картин больше, чем портретов.

«На сколько больше», значит, вычисляется вычитанием.
Оформляем условие в виде краткой записи.
-(2023).jpg)
Рассуждаем.
В зале музея выставили 20 картин. Общее количество картин складывается из количества портретов и пейзажей. Значит, чтобы узнать, сколько пейзажей было в музее, нужно из количества всех картин вычесть количества портретов.
20 − 6 = 14 (к.) – выставили в галерее.
Продолжаем рассуждение.
В зале музея выставили 6 портретов и 12 пейзажей. Чтобы узнать, на сколько больше пейзажей, чем портретов, нужно из количества пейзажей вычесть количество портретов.
14 − 6 = 8 (к.) – на сколько больше.
Запишем ответ.
Ответ: пейзажей на 8 картин больше, чем портретов.
Решение выражением:
(20 – 6) : 6 = 8 (к.)
Отвечаем на вопрос.
Рамка имеет форму прямоугольника со сторонами 30 мм и 15 мм, значит, что и печать на стене такая же, как картины – прямоугольник со сторонами 30 мм и 15 мм.
-(2023).jpg)
Задание на полях страницы.
Какое число лишнее?

48 – лишнее число, потому что оно не делится на 7 без остатка или 7, потому что оно однозначное.
Чтобы понять, какое число лишнее, нужно рассмотреть все числа, проанализировать. Какие они, из каких знаков состоят, на что делятся.
Опишем все числа и на что они делятся.
7 – однозначное число, делится без остатка на 7.
14 – двузначное число, делится без остатка на 2 и на 7.
21 – двузначное число, делится без остатка на 3 и на 7.
28 – двузначное число, делится без остатка на 2, на 4 и на 7.
35 – двузначное число, делится без остатка на 5 и на 7.
42 – двузначное число, делится без остатка на 2, на 3, на 6 и на 7.
48 – двузначное число, делится без остатка на 2, на 3, на 4, на 6 и на 8.
56 – двузначное число, делится без остатка на 2, на 4, на 6, на 7 и на 8.
Делаем вывод.
Решение 1: лишним может быть число 7, потому что оно единственное однозначное число;
Решение 2: лишним может быть число 35 – оно единственное делится на 5.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.