Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 98
- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
.jpg "Математика 4 класс Моро, Волкова - 2 часть страница 98")
Номер 2.
В телевизионной игре одна женщина выиграла 25000 р. По правилам игры десятую часть своего выигрыша она подарила детской больнице. Сколько рублей она подарила детской больнице?
Ответ:
25000 : 10 = 2500 (р.) – женщина подарила детской больнице.
Ответ: 2500 рублей всего женщина подарила детской больнице.
Повтори способы оформления краткой записи к задаче и денежную единицу – рубль.
Оформляем условие в виде краткой записи.
Рассуждаем.
Чтобы узнать, сколько женщина подарила детской больнице, нужно сумму выигрыша разделить на 10.
25000 : 10 = 2500 (р.)
Записываем ответ.
Ответ: 2500 рублей женщина подарила детской больнице.
Номер 3.
Папе 42 года, сыну 7 лет. Во сколько раз папа старше сына?
Ответ:
42 : 7 = 6 (раз) – во столько раз папа старше сына.
Ответ: в 6 раз папа старше сына.
Повтори способы оформления краткой записи к задаче.
Оформляем условие в виде краткой записи.
Рассуждаем.
Чтобы узнать, во сколько раз папа старше сына, нужно возраст папы разделить на возраст сына.
42 : 7 = 6 (раз)
Записываем ответ.
Ответ: в 6 раз во столько раз папа старше сына.
Номер 4.
Используя данные таблицы, составь и реши задачи, в которых нужно узнать, сколько краски или лака потребуется для покрытия пола комнаты площадью 16 м²; 24 м²; 19 м².
Задача 1:
Пол в трех комнатах площадью 16 м², 24 м², 19 м² нужно покрасить краской в 2 слоя. Расход краски 120 г на 1 м². Сколько краски потребуется для каждой комнаты?
120 ∙ 16 ∙ 2 = 1920 ∙ 2 = 3840 (г) = 3 кг 840 г
120 ∙ 24 ∙ 2 = 2880 ∙ 2 = 5760 (г) = 5 кг 760 г
120 ∙ 19 ∙ 2 = 2280 ∙ 2 = 4560 (г) = 4 кг 560 г
Ответ: 3 кг 840 г краски нужно на покрас первой комнаты, 5 кг 760 г краски нужно на покрас второй комнаты, 4 кг 560 г краски нужно на покрас третьей комнаты.
Задача 2:
В трёх комнатах решили покрыть лаком пол в 3 слоя. Площадь одной комнаты 24 м², другой 19 м² и третьей 16 м². Расход лака составляет 100 г на 1 м². Сколько лака нужно купить для каждой комнаты?
24 ∙ 100 ∙ 3 = 2400 ∙ 3 = 7200 (г) = 7 кг 200 г
19 ∙ 100 ∙ 3 = 1900 ∙ 3 = 5700 (г) = 5 кг 700 г
16 ∙ 100 ∙ 3 = 1600 ∙ 3 = 4800 (г) = 4 кг 800 г
Ответ: 7 кг 200 г лака нужно для первой комнаты, 5 кг 700г лака нужно для второй комнаты, 4 кг 800 г лака нужно для третьей комнаты.
Повтори единицы массы – килограмм и грамм и единицы площади.
Шаг 1.
Составим первую задачу.
Пол в трех комнатах площадью 16 м², 24 м², 19 м² нужно покрасить краской в 2 слоя. Расход краски 120 г на 1 м². Сколько краски потребуется для каждой комнаты?
Рассуждаем.
Узнаем, сколько краски потребуется для комнаты площадью 16 м².
120 ∙ 16 ∙ 2 = 1920 ∙ 2 = 3840 (г) = 3 кг 840 г
Продолжаем рассуждение.
Узнаем, сколько краски потребуется для комнаты площадью 24 м².
120 ∙ 24 ∙ 2 = 2880 ∙ 2 = 5760 (г) = 5 кг 760 г
Продолжаем рассуждение.
Узнаем, сколько краски потребуется для комнаты площадью 19 м².
120 ∙ 19 ∙ 2 = 2280 ∙ 2 = 4560 (г) = 4 кг 560 г
Записываем ответ.
Ответ: 3 кг 840 г, 5 кг 760 г, 4 кг 560 г.
Шаг 1.
Составим вторую задачу.
В трёх комнатах решили покрыть лаком пол в 3 слоя. Площадь одной комнаты 24 м², другой 19 м² и третьей 16 м². Расход лака составляет 100 г на 1 м². Сколько лака нужно купить для каждой комнаты?
Рассуждаем.
Узнаем, сколько краски потребуется для комнаты площадью 16 м².
16 ∙ 100 ∙ 3 = 1600 ∙ 3 = 4800 (г) = 4 кг 800 г
Продолжаем рассуждение.
Узнаем, сколько краски потребуется для комнаты площадью 24 м².
24 ∙ 100 ∙ 3 = 2400 ∙ 3 = 7200 (г) = 7 кг 200 г
Продолжаем рассуждение.
Узнаем, сколько краски потребуется для комнаты площадью 19 м².
19 ∙ 100 ∙ 3 = 1900 ∙ 3 = 5700 (г) = 5 кг 700 г
Записываем ответ.
Ответ: 7 кг 200 г, 5 кг 700г, 4 кг 800 г.
Номер 5.
Начерти план каждого участка и покажи на нём те объекты, о которых говорится в задачах.
1) Длина прямоугольного поля 500 м, а ширина на 220 м меньше. Седьмую часть этого поля занимает овёс, одну вторую часть – пшеница, а остальную площадь – рожь. Какую площадь занимает рожь?
2) Площадь садового участка 600 м². На нём стоит дом длиной 6 м и шириной 4 м. Из остальной площади участка одну третью часть отвели под сад, а одну четвёртую – под огород. Сколько свободного места осталось на этом участке?
Задача 1:
.jpg "Изображение математика 4 класс Моро, Бантова - 2 часть страница 98, номер 5, задача 1")
1) 500 − 220 = 280 (м) – ширина поля.
2) 500 ∙ 280 = 140000 (м²) – площадь поля.
3) 140000 : 7 = 20000 (м²) – занято овсом.
4) 140000 : 2 = 70000 (м²) – занято пшеницей.
5) 20000 + 70000 = 90000 (м²) – занято овсом и пшеницей.
6) 140000 − 90000 = 50000 (м²) – занято рожью.
Ответ: площадь, занятая рожью составляет 50000 м².
Задача 2:
.jpg "Изображение математика 4 класс Моро, Бантова - 2 часть страница 98, номер 5, задача 2")
1) 6 ∙ 4 = 24 (м²) – площадь дома.
2) 600 − 24 = 576 (м²) – площадь без учета дома.
3) 576 : 3 = 192 (м²) – сад.
4) 576 : 4 = 144 (м²) – огород.
5) 192 + 144 + 24 = 360 (м²) – занято.
6) 600 − 360 = 240 (м²) – свободно.
Ответ: 240 м² поля свободно от посевов.
Повтори единицу длины – метр, единицы площади, что такое доли, а также как найти площадь прямоугольника.
Шаг 1.
Оформляем условие в виде краткой записи и схематического чертежа.
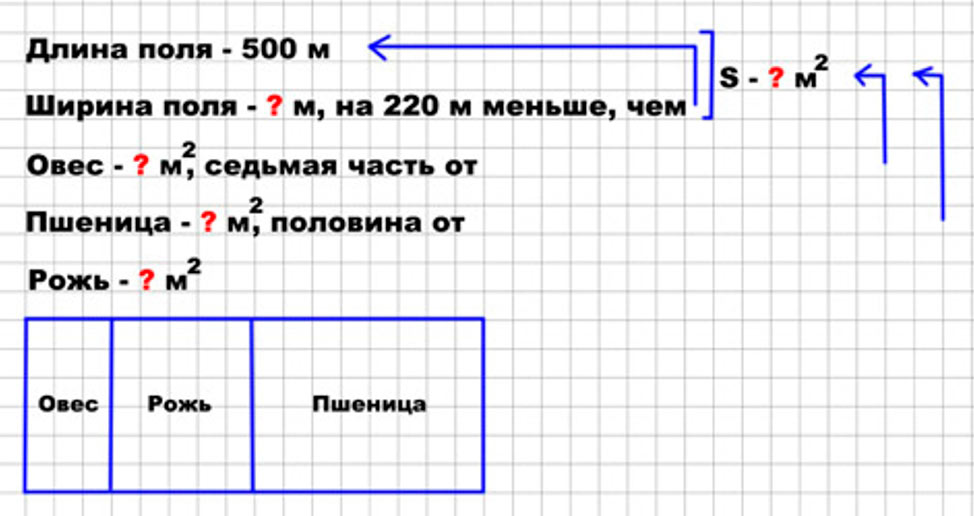
Рассуждаем.
Узнаем, чему равна ширина поля.
1) 500 − 220 = 280 (м) – ширина поля.
Продолжаем рассуждение.
Узнаем, чему равна площадь поля.
2) 500 ∙ 280 = 140000 (м²) – площадь поля.
Продолжаем рассуждение.
Узнаем, сколько м² занято овсом.
3) 140000 : 7 = 20000 (м²) – занято овсом.
Продолжаем рассуждение.
Узнаем, сколько м² занято пшеницей.
4) 140000 : 2 = 70000 (м²) – занято пшеницей.
Продолжаем рассуждение.
Узнаем, сколько м² занято овсом и пшеницей.
5) 20000 + 70000 = 90000 (м²) – занято овсом и пшеницей.
Продолжаем рассуждение.
Узнаем, сколько м² занято рожью.
6) 140000 − 90000 = 50000 (м²)
Записываем ответ.
Ответ: 50000 м² занято рожью.
Шаг 1.
Оформляем условие в виде краткой записи и схематического чертежа.
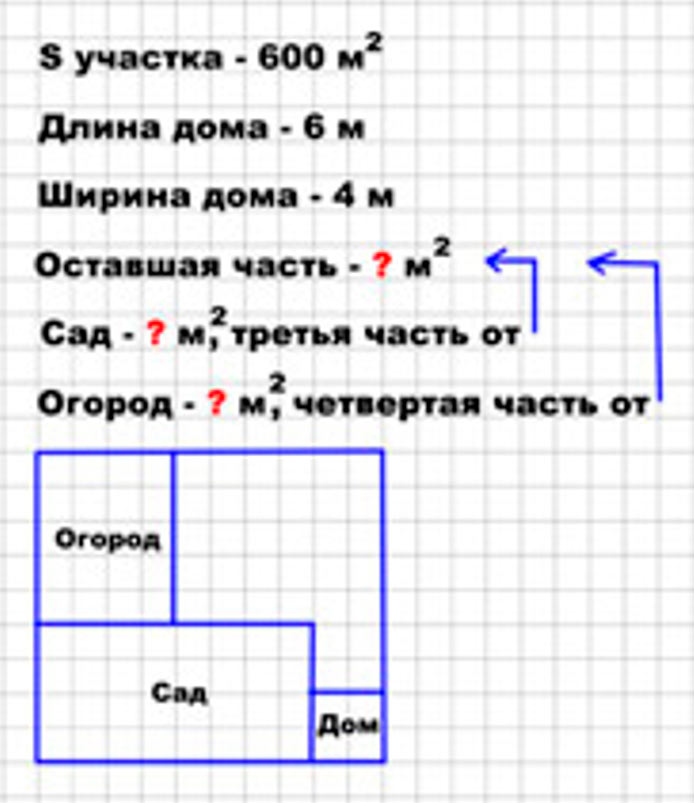
Рассуждаем.
Вычислим, чему равна площадь дома.
1) 6 ∙ 4 = 24 (м²) – площадь дома.
Продолжаем рассуждение.
Вычислим, чему равна площадь без учета дома.
2) 600 − 24 = 576 (м²) – площадь без учета дома.
Продолжаем рассуждение.
Узнаем, сколько м² занимает сад.
3) 576 : 3 = 192 (м²) – сад.
Продолжаем рассуждение.
Узнаем, сколько м² занимает огород.
4) 576 : 4 = 144 (м²) – огород.
Продолжаем рассуждение.
Узнаем, сколько м² занято.
5) 192 + 144 + 24 = 360 (м²) – занято.
Продолжаем рассуждение.
Узнаем, сколько м² свободно.
6) 600 − 360 = 240 (м²)
Записываем ответ.
Ответ: 240 м² свободно.
Номер 6.
Площадь огорода 500 м². На каждый квадратный метр площади высаживали по 300 г картофеля. Сколько килограммов картофеля собрали с этого огорода, если с каждого квадратного метра собирали в 6 раз больше, чем сажали?
Ответ:
1) 300 ∙ 500 = 150000 (г) = 150 (кг) – масса высаженного картофеля. 2) 150 ∙ 6 = 900 (кг) – масса собранного картофеля.
1) 300 ∙ 6 = 1800 (г) – картофеля собрали с 1 м². 2) 1800 ∙ 500 = 900000 (г) = 900 (кг) – масса собранного картофеля.
Ответ: общая масса собранного картофеля составляет 900 кг.
Повтори единицы массы – грамм и килограмм, а также единицы площади.
Оформляем условие в виде таблицы.
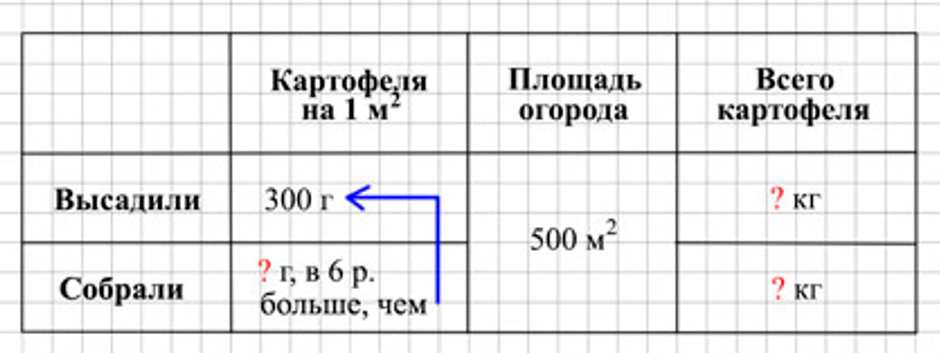
Рассуждаем.
Узнаем массу высаженного картофеля.
1) 300 ∙ 500 = 150000 (г) = 150 (кг) – масса высаженного картофеля.
Продолжаем рассуждение.
Узнаем массу собранного картофеля.
2) 150 ∙ 6 = 900 (кг)
Записываем ответ.
Ответ: 900 кг масса собранного картофеля.
Номер 7.
Узнай площадь прямоугольного участка, если одна седьмая его часть составляет 28 м².
Ответ:
Площадь седьмой части – 28 м²
Площадь участка – ? м²
28 ∙ 7 = 196 (м²) – площадь прямоугольника.
Ответ:площадь прямоугольника составляет 196 м².
Повтори единицы площади, а также что такое доли.
Оформляем условие в виде краткой записи.
Площадь седьмой части – 28 м²
Площадь участка – ? м²
Рассуждаем.
Вычислим, чему равна площадь прямоугольника.
28 ∙ 7 = 196 (м²)
Записываем ответ.
Ответ: 196 м² площадь прямоугольника.
Номер 8.
С каждых 100 м² опытного участка было собрано по 46 кг зерна нового сорта пшеницы. Сколько центнеров зерна при такой урожайности можно было бы получиться с 10000 м²?
Ответ:
100 м² – 46 кг
10000 м² – ? кг
1) 10000 : 100 = 100 (раз) – во столько раз пшеницы может быть собрано на возможном участке.
Во сколько раз больше участок, во столько раз больше и будет урожай пшеницы.
2) 100 ∙ 46 = 4600 (кг) = 46 ц – зерна можно было бы получить при такой же урожайности с участка площадью 10000 м².
Ответ: 46 ц зерна можно было получить при такой урожайности.
Повтори единицы массы – килограмм и центнер, а также единицы площади.
Оформляем условие в виде краткой записи.
100 м² – 46 кг
10000 м² – ? кг
Рассуждаем.
Узнаем, во столько раз пшеницы может быть собрано на возможном участке.
1) 10000 : 100 = 100 (раз) – во столько раз пшеницы может быть собрано на возможном участке.
Продолжаем рассуждение.
Во сколько раз больше участок, во столько раз больше и будет урожай пшеницы.
2) 100 ∙ 46 = 4600 (кг) = 4 т 6 ц
Записываем ответ.
Ответ: 4 т 6 ц зерна можно было бы получить при такой же урожайности с участка площадью 10000 м².
Задание на полях страницы
Ребус.
Ответ:
Перед нами ребус, для того чтобы найти недостающие цифры необходимо выполнить умножение.
Рассмотрим ребус.
Разгадаем ребус.
Умножаем на единицы. На какое число надо умножить 3, чтобы получилось 9? Это число 3. 3 ∙ 3 = 9
4 ∙ 3 = 12. Пишу 2 под десятками, а 1 сот. запомню и прибавлю к сотням после умножения сотен.
После того, как к сотням прибавили 1 сот., которая получилась при умножении десятков, под сотнями записали 7. 7 – 1 = 6.
Какое число надо умножить на 3, чтобы получилось 6? Это число 2.
Какое число надо умножить на 3, чтобы получилось двузначное число с 5 единицами? Это число 5. 5 ∙ 3 = 15
Умножаем на десятки. На какое число надо умножить 3, чтобы получилось 2 в конце числа? Это число 4. 3 ∙ 4 = 12.
Умножаем десятки. 4 ∙ 4 = 16. 16 + 1 = 17
Умножаем сотни. 2 ∙ 4 = 8. 8 + 1 = 9
5 ∙ 4 = 20
Складываем неполные произведения. 215449.
Оформим задание в тетрадь.
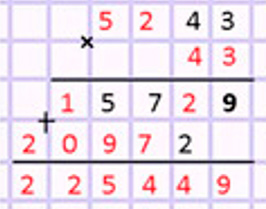
Геометрические фигуры
Номер 1.
Назови знакомые тебе геометрические фигуры, начерти их в тетради и обозначь буквами.
Ответ:
Номер 2.
Что ты знаешь о многоугольниках? Сколько вершин, углов и сторон у двенадцатиугольника?
Ответ:Многоугольник это плоская замкнутая ломаная без самопересечений. Вершины ломаной называются вершинами многоугольника, а её звенья — сторонами многоугольника. Многоугольники называются по количеству углов-3 угла это треугольник, 4 угла это четырехугольник и т.д. В любом многоугольнике число углов равно числу сторон и вершин. В двенадцатиугольнике 12 углов, 12 вершин и 12 сторон.
Номер 3.
Какие виды треугольников ты знаешь? Может ли прямоугольный треугольник быть равносторонним? разносторонним? Может ли тупоугольный треугольник быть равнобедренным? Начерти в тетради равнобедренный прямоугольный треугольник.
Ответ:
Номер 4.
Какие виды четырёхугольников ты знаешь? Продолжи предложения:
Ответ:
Виды четырехугольников: прямоугольник, квадрат, ромб.
1) Прямоугольник – это четырехугольник, у которого все углы прямые.
2) Квадрат – это прямоугольник, у которого все стороны равны.
Номер 5.
1) Среди четырёхугольников, изображённых на рисунке 1, найди прямоугольники и запиши их названия; подчеркни название квадрата.
2) Найди периметр прямоугольника ОРКС и площадь квадрата. Объясни, почему четырёхугольник ABCD нельзя назвать квадратом.
Ответ:
2) Периметр ОРКС = (15 мм + 9 мм) ∙ 2 = 30 мм + 18 мм = 48 мм = 4 см 8 мм.
Площадь FEKM = 9 мм ∙ 9 мм = 81 м².
Прямоугольник АBCD нельзя назвать квадратом, потому что квадрат-прямоугольник, а у прямоугольника углы прямые. В ромбе ABCD углы не прямые.
Номер 6.
Определи вид каждого треугольника, если его периметр находят так: 1) 3 + 4 + 5 = 12 (см); 2) 3 ∙ 2 + 4 = 10 (см); 3) 5 ∙ 3 = 15 (см).
Ответ:1) Так находят периметр разностороннего треугольника, ведь он имеет разные длины сторон. В данном случае 3, 4 и 5. 2) Так находят периметр равнобедренного треугольника, ведь две его стороны равны (умножением нашли их сумму) и прибавили 4 – длина третьей стороны. 3) Так находят периметр равностороннего треугольника, стороны которого равны.
Номер 7.
Рассмотри рисунок 2 на полях и запиши названия всех прямоугольных, остроугольных и тупоугольных треугольников; подчеркни названия равнобедренных треугольников.
Прямоугольные треугольники: KAD, KBO, ABO, KBC, DCO.
.jpg "Математика 4 класс Моро, Бантова - 2 часть страница 98, номер 7, 2024 год.")
Номер 8.
Начерти 2 окружности с радиусами 2 см и 3 см сначала с общим центром, а потом с разными центрами.
Ответ:
Номер 9.
Найди длину ломаной АОКС (рис. 2).
Ответ:AOKC = АО + ОК + КС = 30 + 30 + 40 = 100 мм = 10 см
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽
Напишите свой комментарий.