Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 6

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Задание вверху страницы.
1) Черепаха двигалась со скоростью 5 м/мин. Какое расстояние прошла она за 3 мин?
2) Слон двигался со скоростью 100 м/мин. Какое расстояние он прошел за 10 мин?
3) Рассмотри таблицу и объясни, как можно найти расстояние, если известны скорость и время движения.

1) Ответ: чтобы найти расстояние, нужно скорость умножить на время. S = 5 ∙ 3 = 15 (м) – прошла черепаха за 3 минуты. 2) Ответ: чтобы найти расстояние, нужно скорость умножить на время. S = 100 ∙ 10 = 1000 (м) – прошёл слон за 10 минут. 3) Ответ: чтобы найти расстояние, нужно известные скорость и время перемножить, то есть S = V ∙ t.
S = V ∙ t: Чтобы найти расстояние, надо скорость умножить на время.
V = S : t: Чтобы найти скорость, надо расстояние разделить на время.
t = S : V: Чтобы найти время, надо расстояние разделить на скорость.
Рассмотрим таблицу и ответим на вопросы задания.
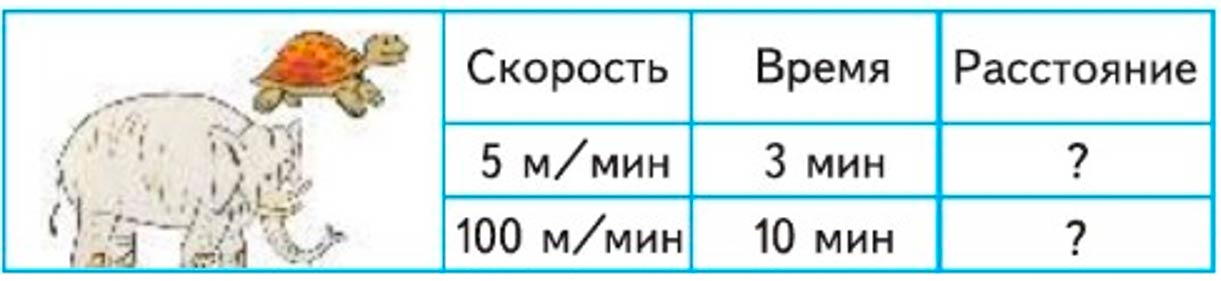
Найдем расстояние, которое прошла черепаха.
Чтобы найти расстояние, нужно скорость умножить на время.
5 ∙ 3 = 15 (м) – прошла черепаха за 3 минуты.
Найдем расстояние, которое прошел слон.
Чтобы найти расстояние, нужно скорость умножить на время.
100 ∙ 10 = 1000 (м) – прошёл слон за 10 минут.
Ответим на вопрос задания.
S = V ∙ t: Чтобы найти расстояние, надо скорость умножить на время.
Номер 14.
Таня пробежала 30 м за 6 с. С какой скоростью она бежала?
Ответ:
30 : 6 = 5 (м/с)
Ответ: скорость, с которой бежала Таня - 5 м/с.
S = V ∙ t: Чтобы найти расстояние, надо скорость умножить на время.
V = S : t: Чтобы найти скорость, надо расстояние разделить на время.
t = S : V: Чтобы найти время, надо расстояние разделить на скорость.
Оформляем условие в виде таблицы.

Рассуждаем
Чтобы узнать скорость, с которой двигалась Таня, нужно расстояние разделить на время.
30 : 6 = 5 (м/с)
Записываем ответ.
Ответ: 5 м/с скорость.
Номер 15.
Мотоциклист ехал 3 ч со скоростью 60 км/ч и 2 ч со скоростью 70 км/ч. Какое расстояние он проехал за всё это время? Объясни, что обозначает выражение 60 ∙ 3 - 70 ∙ 2.

1) 60 ∙ 3 = 180 (км) – проехал за 3 часа.
2) 70 ∙ 2 = 140 (км) – проехал за 2 часа.
3) 180 + 140 = 320 (км)
60 ∙ 3 + 70 ∙ 2 = 320 (км)
Ответ: 320 км проехал мотоциклист.
60 ∙ 3 − 70 ∙ 2 – на сколько км больше проехал за 1-ые три часа, чем за 2-ые два часа
S = V ∙ t: Чтобы найти расстояние, надо скорость умножить на время.
V = S : t: Чтобы найти скорость, надо расстояние разделить на время.
t = S : V: Чтобы найти время, надо расстояние разделить на скорость.
Оформляем условие в виде таблицы.

Рассуждаем.
Узнаем, какое расстояние мотоциклист проехал за три часа.
1) 3 ∙ 60 = 180 (км) − проехал мотоциклист со скоростью 60 км/ч;
Продолжаем рассуждение.
Узнаем, какое расстояние мотоциклист проехал за два часа.
2) 2 ∙ 70 = 140 (км) − проехал мотоциклист со скоростью 70 км/ч;
Продолжаем рассуждение.
Узнаем, какое расстояние мотоциклист проехал за все это время.
3) 180 + 140 = 320 (км) − мотоциклист проехал всего.
Записываем ответ.
Ответ: 320 км.
Объясним, что обозначает данное выражение.
60 ∙ 3 − 70 ∙ 2 = 180 − 140 = на 40 (км) − больше проехал мотоциклист со скоростью 60 км/ч, чем со скоростью 70 км/ч.
Номер 16.
Составь по выражению 80 ∙ 4 − 60 ∙ 4 задачи с величинами: скорость, время, расстояние (с. 10 – 11).
Ответ:
Петя вместе с родителями поехали на своей машине летом к бабушке в деревню. Сначала они ехали 4 часа по асфальтированной дороге со скоростью 80 км/ч. После небольшой остановки с посещением кафе, они продолжили свой путь. Дальше они ехали 4 часа по грунтовой дороге со скоростью 60 км/ч. На сколько километров больше они проехали до остановки, чем после неё?
1) 80 ∙ 4 − 60 ∙ 4 = 80 (км)
Ответ: на 80 км больше они проехали до остановки, чем после неё.
S = V ∙ t: Чтобы найти расстояние, надо скорость умножить на время.
V = S : t: Чтобы найти скорость, надо расстояние разделить на время.
t = S : V: Чтобы найти время, надо расстояние разделить на скорость.
Составим и решим первую задачу по данному выражению.
Папа ехал из дома в деревню 4 часа со скоростью 80 км/ч, а затем возвращался по той же дороге, но уже со скоростью 60 км/ч. Какое расстояние осталось проехать папе до дома после 4 часов пути обратно?
Решение:
80 ∙ 4 − 60 ∙ 4 = 320 − 240 = 80 (км) − осталось проехать папе до дома.
Ответ: 80 км.
Составим и решим вторую задачу по данному выражению.
Со станции в одно и тоже время выехали два поезда: пассажирский и товарный. На сколько км больше проехал пассажирский поезд, чем товарный за 4 часа пути, если скорость пассажирского поезда − 80 км/ч, а товарного − 60 км/ч?
Решение:
80 ∙ 4 − 60 ∙ 4 = 320 − 240 = на 80 (км) − пассажирский поезд проехал больше, чем товарный.
Ответ: на 80 км.
Номер 17.

Длина и ширина одной из комнат дачного дома 6 м и 5 м, а другой – 5 м и 4 м. Узнай, сколько граммов лака расходуется на 1 м2 пола, и рассчитай, сколько лака потребуется, чтобы покрыть пол в этих комнатах (с. 98, № 4).
Ответ:а1 = 6 м
b1 = 5 м
а2= 5 м
b2 = 4 м
S – ? м2
S = a ∙ b
1) 6 ∙ 5 + 5 ∙ 4 = 50 (м2) – площадь всех комнат.

2) 100 ∙ 50 = 5000 (г)
Ответ: 5 кг лака потребуется.
1) 6 ∙ 5 = 30 (м2) – площадь 1 комнаты
2) 5 ∙ 4 = 20 (м2) – площадь 2 комнаты
3) 100 ∙ 3 = 300 (г) – расходуется лака на 1 м2
4) 300 ∙ 30 = 9 000 (г) = 9 (кг) – потребуется лака для 1 комнаты
5) 300 ∙ 20 = 6 000 (г) – 6 (кг) – потребуется лака для 2 комнаты
6) 9 + 6 = 15 (кг) – потребуется лака
Ответ: 300 г; 15 кг.
Длина – величина, характеризующая протяженность объекта на плоскости, выражается в таких единицах измерения, как миллиметр, сантиметр, дециметр, метр, километр.
Помни о соотношении числовых значений единиц измерения длины:
1 см = 10 мм
1 дм = 10 см
1 м = 100 см
1 м = 10 дм
1 км = 1000 м
Площадь – величина, которая характеризует размер части плоскости, занятой фигурой. Измеряется в таких единицах измерения, как: мм2, см2, дм2, м2, км2 и др.
Помни о соотношении числовых значений единиц измерения площади:
1 см2 = 100 мм2
1 дм2 = 100 см2
1 м2 = 10 000 см2
1 м2 = 100 дм2
Оформляем условие в виде краткой записи.
а1 = 6 м
b1 = 5 м
а2= 5 м
b2 = 4 м
S – ? м2
Рассуждаем.
Найдем площадь двух комнат. Для этого воспользуемся формулой нахождения площади.
S = a ∙ b
1) 6 ∙ 5 + 5 ∙ 4 = 50 (м2) – площадь 2-х комнат.
Продолжаем рассуждение.
Составим таблицу и вычислим, сколько лака потребуется для этих комнат.

2) 50 ∙ 100 = 5000 (г)
5000 г = 5 кг
Записываем ответ.
Ответ: 5 кг лака потребуется.
Длина и ширина одной из комнат дачного дома 6 м и 5 м, а другой – 5 м и 4 м. Сколько граммов лака потребуется, чтобы покрыть пол в этих двух комнатах в 2 слоя? Дополни текст необходимыми для задачи данными (с. 100, № 4) и реши задачу.
Ответ:Таблица со с. 100, № 4.

а1 = 6 м
b1 = 5 м
а2 = 5 м
b2 = 4 м
S – ? м2
1) 6 ∙ 5 = 30 (м2) – площадь 1 комнаты.
2) 5 ∙ 4 = 20 (м2) – площадь 2 комнаты.
3) 30 + 20 = 50 (м2) – общая площадь.
4) 50 · 100 = 5000 (г) = 5 (кг) – потребуется лака на 1 слой.
5) 5 · 2 = 10 (кг) – потребуется лака на 2 слоя.
Ответ: 10 кг лака всего потребуется для покрытия на 2 слоя.
1) Длина – величина, характеризующая протяженность объекта на плоскости.
2) Помни о соотношении числовых значений единиц измерения длины:
1 см = 10 мм, 1 дм = 10 см, 1 м = 100 см, 1 м = 10 дм, 1 км = 1000 м.
3) Площадь – величина, которая характеризует размер части плоскости, занятой фигурой.
4) Помни о соотношении числовых значений единиц измерения площади:
1 см2 = 100 мм2, 1 дм2 = 100 см2, 1 м2 = 10 000 см2, 1 м2 = 100 дм2.
Оформляем краткую запись.
а1 = 6 м
b1 = 5 м
а2 = 5 м
b2 = 4 м
S – ? м2
Рассуждаем.
Чтобы найти площадь двух комнат, нужно найти площадь каждой из комнат, а потом сложить их. Для этого воспользуемся формулой нахождения площади.
S = a ∙ b
6 ∙ 5 = 30 (м2) – площадь одной комнаты;
5 ∙ 4 = 20 (м2) – площадь другой комнаты;
30 + 20 = 50 (м2) – общая площадь.
Продолжаем рассуждение.
На 1 м2 нужно 100 г лака для пола, чтобы покрыть в 1 слой. Но по условию задачи требуется покрыть пол двумя слоями лака.
50 ∙ 100 = 5000 (г) = 5 (кг) – лака потребуется на 1 слой;
5 ∙ 2 = 10 (кг) – лака потребуется на 2 слоя.
Записываем ответ.
Ответ: 10 кг лака потребуется.
Номер 18.
В каком уравнении каждой пары значение x будет больше? Подтверди свои ответы решениями уравнений.
Ответ:
При одинаковой сумме значение х будет больше в том уравнении, где известный множитель меньше (20 < 120).
х + 120 = 40 ∙ 5
х + 120 = 200
х = 200 − 120
х = 80
80 + 120 = 40 ∙ 5
200 = 200
Ответ: х = 80.
х + 20 = 40 ∙ 5
х + 20 = 200
х = 200 − 20
х = 180
180 + 20 = 40 ∙ 5
200 = 200
Ответ: х = 180.
При одинаковом значении произведения Х будет больше в том уравнении, где известный множитель меньше (5 < 10). Значит, в первом уравнении значение Х будет больше.
х ∙ 5 = 240
х = 240 : 5
х = 48
48 ∙ 5 = 240
240 = 240
Ответ: х = 48.
х ∙ 10 = 240
х = 240 : 10
х = 24
24 ∙ 10 = 240
240 = 240
Ответ: х = 24.
При одинаковом значении произведения Х будет больше в том уравнении, где известный множитель меньше (8 < 9). Значит, во втором уравнении значение Х будет больше.
9 ∙ х = 72
х = 72 : 9
х = 8
9 ∙ 8 = 72
72 = 72
Ответ: х = 8.
8 ∙ х = 72
х = 72 : 8
х = 9
8 ∙ 9 = 72
72 = 72
Ответ: х = 9.
Уравнение – равенство с неизвестной, при подстановке числа в которую, получается верное равенство.
Вспомни названия компонентов действия умножения, и зависимость между компонентами и результатом действия умножения:
1 множитель ∙ 2 множитель = значение произведения.
Значение произведения : 1 множитель = 2 множитель.
Значение произведения : 2 множитель = 1 множитель.
Уменьшаемое – вычитаемое = значение разности.
Уменьшаемое – значение разности = вычитаемое.
Значение разности + вычитаемое = уменьшаемое.
Делимое : делитель = значение разности.
Делимое : значение разности = делитель.
Значение разности ∙ делитель = делимое
Рассмотрим первую пару уравнений и вычислим их значения.
При одинаковой сумме значение х будет больше в том уравнении, где известный множитель меньше (20 < 120).
х + 120 = 40 ∙ 5
х + 120 = 200
х = 200 − 120
х = 80
Проверка:
80 + 120 = 40 ∙ 5
200 = 200
Ответ: х = 80.
х + 20 = 40 ∙ 5
х + 20 = 200
х = 200 − 20
х = 180
Проверка:
180 + 20 = 40 ∙ 5
200 = 200
Ответ: х = 180.
Рассмотрим вторую пару уравнений и вычислим их значения.
При одинаковом значении произведения х будет больше в том уравнении, где известный множитель меньше (5 < 10). Значит, в первом уравнении значение х будет больше.
х ∙ 5 = 240
х = 240 : 5
х = 48
Проверка:
48 ∙ 5 = 240
240 = 240
Ответ: х = 48.
х ∙ 10 = 240
х = 240 : 10
х = 24
Проверка:
24 ∙ 10 = 240
240 = 240
Ответ: х = 24.
Рассмотрим третью пару уравнений и вычислим их значения.
При одинаковом значении произведения х будет больше в том уравнении, где известный множитель меньше (8 < 9). Значит, во втором уравнении значение х будет больше.
9 ∙ х = 72
х = 72 : 9
х = 8
Проверка:
9 ∙ 8 = 72
72 = 72
Ответ: х = 8.
8 ∙ х = 72
х = 72 : 8
х = 9
Проверка:
8 ∙ 9 = 72
72 = 72
Ответ: х = 9.
Номер 19.
Ответ:

Помним о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Выполняем вычисления по действиям.


Оформляем задание в тетрадь.

Номер 20.
Какой будет площадь квадрата, который можно составить из этих фигур? Составь и начерти его.


S к. = 5 кл. ∙ 5 кл. = 25 кл2
2-й способ решения:
Способ решения 1: посчитать все квадратики с площадью 1 см2 всех фигур.
Все фигуры по 5 квадратов.
5 + 5 + 5 + 5 + 5 = 5 ∙ 5 = 25 (см2) – площадь квадрата
Способ решения 2: умножить длину и ширину получившегося квадрата.
5 ∙ 5 = 25 (см2) – площадь квадрата
Ответ: 25 см2.
Площадь фигуры – часть плоскости, занятая фигурой. Площадь может измеряться в единицах измерения: мм2, см2, дм2, м2, км2 и др. Площадь прямоугольника – произведение длин его сторон. Вычисляется по формуле: а ∙ в, где а и в – стороны прямоугольника.
Рассмотрим фигуры на полях учебника.

Составим квадрат из данных фигур и найдём его площадь.
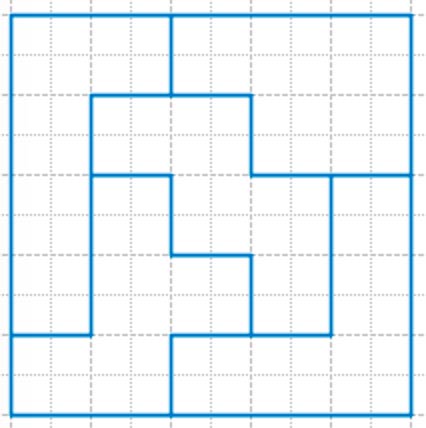
S = 5 ∙ 5 = 25 (см2)
Оформим задание в тетрадь.
Задание внизу страницы
Ответ:
Помним о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Выполняем вычисления по действиям.
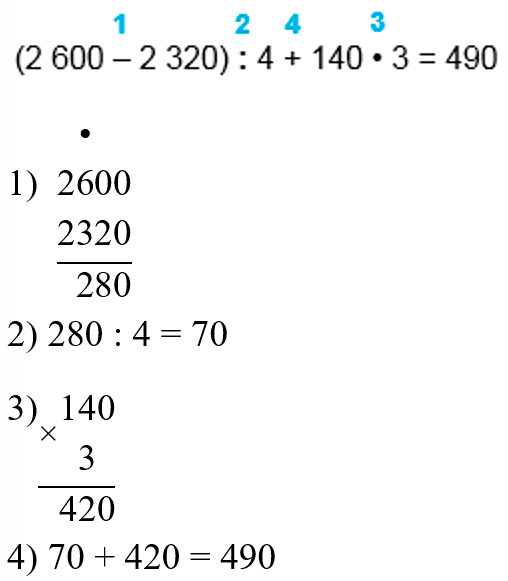
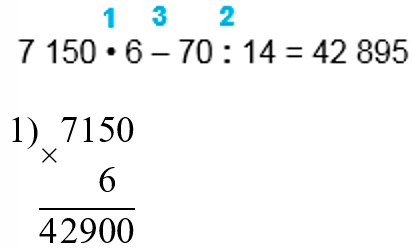
2) 70 : 14 = 5
3) 42 900 – 5 = 42 895
Оформляем задание в тетрадь.
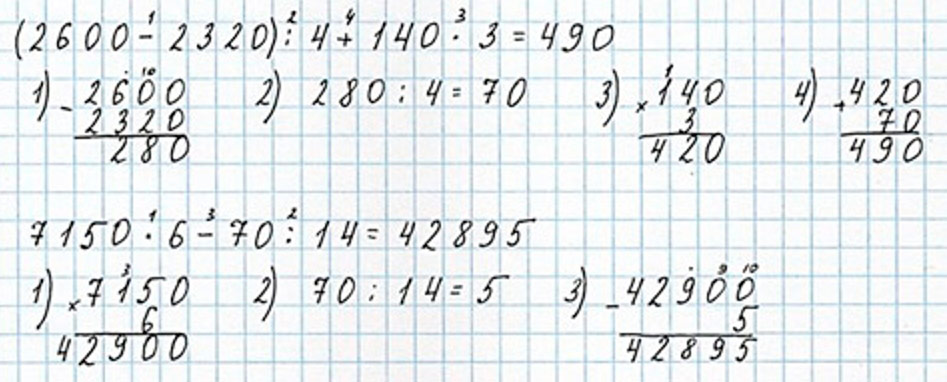
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.