Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 54
- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
.jpg "Математика 4 класс Моро, Волкова - 2 часть страница 54")
Что узнали. Чему научились
Номер 1.
Проверь, верны ли равенства.
Ответ:
13 ∙ (10 + 2) = 13 ∙ 10 + 13 ∙ 2 – верно.
15 ∙ (10 ∙ 2) = 15 ∙ 10 ∙ 2 – верно.
(20 + 5) ∙ 4 = 20 + 5 ∙ 4 – неверно, потому что (20 + 5) ∙ 4 = 20 ∙ 4 + 5 ∙ 4.
72 : (8 ∙ 3) = 72 : 8 ∙ 3 – неверно, потому что 72 : (8 ∙ 3) = 72 : 8 : 3.
Повтори свойства умножения.
Проверим равенства, поясняя свои действия.
Распределительное свойство: при умножении числа на сумму можно умножить его на каждое слагаемое в отдельности и полученные результаты сложить, поэтому
13 ∙ (10 + 2) = 13 ∙ 10 + 13 ∙ 2 – верное равенство.
Проверка:
13 ∙ (10 + 2) = 13 ∙ 12 = 156
13 ∙ 10 + 13 ∙ 2 = 130 + 26 = 156
Сочетательное свойство: два соседних множителя можно заменить их произведением, поэтому
15 ∙ (10 ∙ 2) = 15 ∙ 10 ∙ 2 – верное равенство.
Проверка:
15 ∙ (10 ∙ 2) = 15 ∙ 20 = 300
15 ∙ 10 ∙ 2 = 150 ∙ 2 = 300
Распределительное свойство: при умножении числа на сумму можно умножить его на каждое слагаемое в отдельности и полученные результаты сложить. Поэтому
(20 + 5) ∙ 4 = 20 + 5 ∙ 4 – неверное равенство.
Проверка:
(20 + 5) ∙ 4 = 25 ∙ 4 = 100
20 + 5 ∙ 4 = 20 + 20 = 40
Верным было бы равенство:
(20 + 5) ∙ 4 = 20 ∙ 4 + 5 ∙ 4.
Чтобы разделить какое-нибудь число на произведение, можно разделить это число на первый множитель и полученное частное разделить на второй множитель. Поэтому
72 : (8 ∙ 3) = 72 : 8 ∙ 3 – неверное равенство.
72 : (8 ∙ 3) = 72 : 24 = 3
72 : 8 ∙ 3 = 9 ∙ 3 = 27
Верным было бы равенство:
72 : (8 ∙ 3) = 72 : 8 : 3.
Оформим задание в тетрадь.
13 ∙ (10 + 2) = 13 ∙ 10 + 13 ∙ 2 – верно.
15 ∙ (10 ∙ 2) = 15 ∙ 10 ∙ 2 – верно.
(20 + 5) ∙ 4 = 20 + 5 ∙ 4 – неверно, потому что (20 + 5) ∙ 4 = 20 ∙ 4 + 5 ∙ 4.
72 : (8 ∙ 2) = 72 : 8 ∙ 3 – неверно, потому что 72 : (8 ∙ 2) = 72 : 8 : 2.
Номер 2.
Ответ:
Повтори алгоритм письменного сложения и умножения трёхзначных чисел, а также порядок действий.
Выполняем вычисления по действиям.
Оформляем задание в тетрадь.
(990 – 90) : 100 ∙ 9 = 81
990 – 40 + 25 ∙ 7 ∙ 4 = 1 650
1 000 : (1 000 ∙ 1) – 1 = 0
12 ∙ 5 + (84 – 72 : 3) = 120
Номер 3.
Найди значения выражений a + b и a − b, если: 1) a = 30100 и b = 20935; 2) a = 28005 и b = 13706.
Ответ:1)
.jpg "Изображение математика 4 класс Моро, Бантова - 2 часть страница 54, номер 3, пример 1")
2)
.jpg "Изображение математика 4 класс Моро, Бантова - 2 часть страница 54, номер 3, пример 2")
Повтори, что такое буквенные выражения.
Найдем значения выражений при a = 30100 и b = 20935.
1) Если a = 30 100 и b = 20 935, то
a + b = 30 100 + 20 935 = 51 035
a – b = 30 100 – 20 935 = 9 165
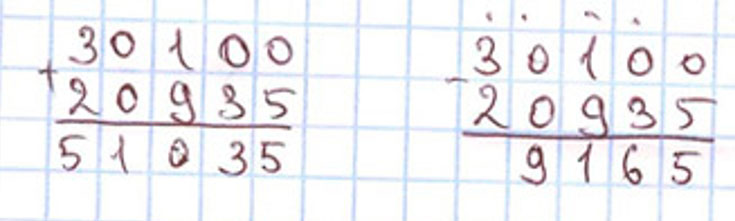
Найдем значения выражений при a = 28005 и b = 13706.
2) Если a = 28 005 и b = 13 706, то
a + b = 28 005 + 13 706 = 41 711
a – b = 28 005 – 13 706 = 14 299
Оформляем задание в тетрадь.
Номер 4.
Найди значения выражений с ∙ d и с : d, если c = 6030 и d = 90.
Ответ:
Повтори, что такое буквенные выражения.
Выполняем вычисления с пояснениями.
Чтобы найти значение буквенного выражения, нужно в это выражение вместо букв подставить данные числа и выполнить вычисления.
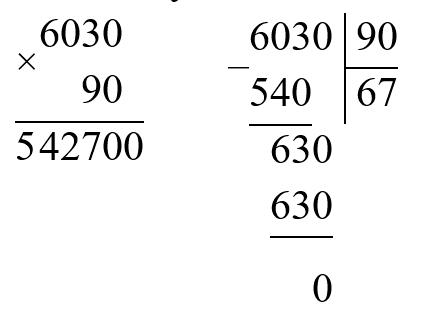
Оформляем задание в тетрадь.
Если c = 6030 и d = 90.
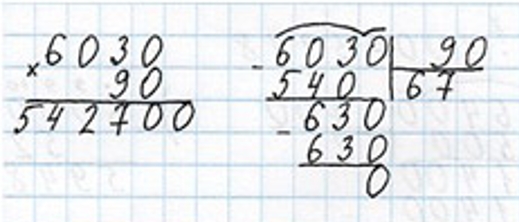
Номер 5.
Вычисли удобным способом.
Ответ:
87 ∙ 64 + 87 ∙ 36 = 87 ∙ (64 + 36) = 87 ∙ 100 = 8700
39 ∙ 16 + 39 ∙ 4 = 39 ∙ (16 + 4) = 39 ∙ 20 = 780
96 ∙ 77 − 96 ∙ 76 = 96 ∙ (77 − 76) = 96 ∙ 1 = 96
48 ∙ 61 − 40 ∙ 61 = 61 ∙ (48 − 40) = 61 ∙ 8 = 488
24 ∙ 49 + 24 = 24 ∙ 49 + 24 ∙ 1 = 24 ∙ (49 + 1) = 24 ∙ 50 = 1200
34 ∙ 21 − 34 = 34 ∙ 21 − 34 ∙ 1 = 34 ∙ (21 − 1) = 34 ∙ 20 = 680
Повтори свойства умножения.
Выполняем вычисления с пояснениями.
Чтобы умножить число на сумму, можно это число умножить на каждое слагаемое и полученные результаты сложить.
Чтобы умножить число на разность, можно это число отдельно умножить на уменьшаемое, затем на вычитаемое и из первого результата вычесть второй.
87 ∙ 64 + 87 ∙ 36 = 87 ∙ (64 + 36) = 87 ∙ 100 = 8 700
39 ∙ 16 + 39 ∙ 4 = 39 ∙ (16 + 4) = 39 ∙ 20 = 780
96 ∙ 77 – 96 ∙ 76 = 96 ∙ (77 – 76) = 96 ∙ 1 = 96
48 ∙ 61 – 40 ∙ 61 = 61 ∙ (46 – 40) = 61 ∙ 6 = 366
24 ∙ 49 + 24 = 24 ∙ 49 + 24 ∙ 1 = 24 ∙ (49 + 1) = 24 ∙ 50 = 1 200
34 ∙ 21 – 34 = 34 ∙ 21 – 34 ∙ 1 = 34 ∙ (21 – 1) = 34 ∙ 20 = 680
Оформляем задание в тетрадь.
87 ∙ 64 + 87 ∙ 36 = 87 ∙ (64 + 36) = 87 ∙ 100 = 8700
39 ∙ 16 + 39 ∙ 4 = 39 ∙ (16 + 4) = 39 ∙ 20 = 780
96 ∙ 77 − 96 ∙ 76 = 96 ∙ (77 − 76) = 96 ∙ 1 = 96
48 ∙ 61 − 40 ∙ 61 = 61 ∙ (48 − 40) = 61 ∙ 8 = 488
24 ∙ 49 + 24 = 24 ∙ 49 + 24 ∙ 1 = 24 ∙ (49 + 1) = 24 ∙ 50 = 1200
34 ∙ 21 − 34 = 34 ∙ 21 − 34 ∙ 1 = 34 ∙ (21 − 1) = 34 ∙ 20 = 680
Номер 6.
Запиши неравенства и проверь, верны ли они.
1) Частное чисел 36150 и 50 меньше разности чисел 2010 и 1285.
2) Произведение чисел 701 и 322 больше, чем 200000.
Повтори, как называются числа при вычитании, умножении и делении, а также что такое неравенства.
Выполняем вычисления.
1) 36 150 : 50 < 2 010 – 1 285 – верно
2) 701 ∙ 322 > 200 000 – верно
Оформляем задание в тетрадь.
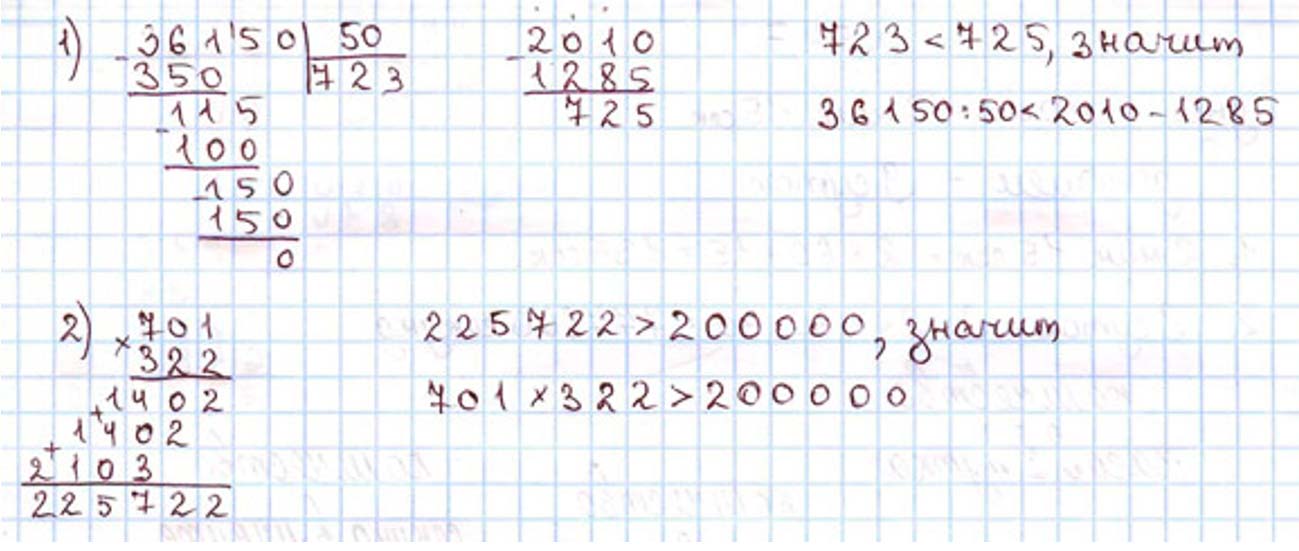
Номер 7.
Ответ:
Повтори алгоритм умножения на трёхзначные числа.
Выполняем вычисления с пояснениями.
Пишу: 144 ∙ 702.
Умножу первый множитель на число единиц:
144 ∙ 2 = 288.
Получу первое неполное произведение: 288.
В десятках второго множителя – ноль, поэтому пропускаем этап умножения на десятки.
Умножу первый множитель на число сотен:
144 ∙ 7 = 1 008.
Получу второе неполное произведение: 1 008 сот.
Начну подписывать второе неполное произведение под сотнями.
Сложу неполные произведения.
Читаю ответ: 101 088. Это произведение чисел 144 и 702.
Пишу: 588 ∙ 320.
Ноль смещаем вправо и не учитываем его в умножении.
Умножу первый множитель на число единиц:
588 ∙ 2 = 1 176.
Получу первое неполное произведение: 1 176.
Умножу первый множитель на число десятков:
588 ∙ 3 = 1764.
Получу второе неполное произведение: 1 764 дес.
Начну подписывать второе неполное произведение под десятками.
Сложу неполные произведения. Допишу к ответу справа ноль из второго множителя.
Читаю ответ: 130 160. Это произведение чисел 588 и 320.
Далее рассуждаем аналогично.
Выполняем вычисления и оформляем задание в тетрадь.
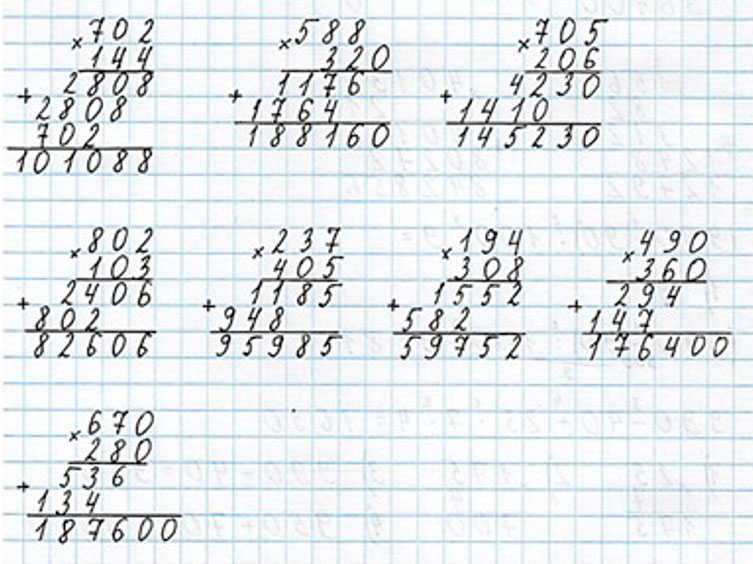
Номер 8.
Ответ:
Повтори алгоритм письменного сложения, вычитания, умножения и деления на трёхзначное число, а также порядок действий.
Выполняем вычисления по действиям.
Оформляем задание в тетрадь.
720 ∙ 400 – 195 046 = 92 954
83 249 + 6 710 ∙ 80 = 620 049
264 037 + 516 600 : 900 – 17 080 = 247 531
450 430 – 196 000 : 700 + 98 764 = 548 914
Номер 9.
Выполни деление с остатком и проверь решение.
Ответ:
Повтори, как выполняется деление с остатком.
Вспомним, как выполнять проверку.
Проверка:
1) Остаток должен быть меньше делителя.
2) Умножим частное на делитель.
3) Прибавим к результату остаток. Сумма должна быть равна делимому.
Выполняем вычисления и оформляем задание в тетрадь.
Номер 10.
Используя эти выражения, составь верные равенства.
Ответ:
32 ∙ 40 + 32 ∙ 6 = 32 ∙ 46
23 ∙ 50 + 23 ∙ 4 = 23 ∙ 54
46 ∙ 30 + 46 ∙ 2 = 46 ∙ 32
54 ∙ 20 + 54 ∙ 3 = 54 ∙ 23
32 ∙ 40 + 32 ∙ 6 = 46 ∙ 30 + 46 ∙ 2
23 ∙ 50 + 23 ∙ 4 = 54 ∙ 20 + 54 ∙ 3
23 ∙ 54 = 54 ∙ 23
32 ∙ 46 = 46 ∙ 32
Повтори, что такое равенства.
Выполняем вычисления с пояснениями.
Чтобы умножить число на сумму, можно умножить это число на каждое слагаемое и сложить полученные результаты.
32 ∙ 40 + 32 ∙ 6 = 32 ∙ (40 + 6) = 32 ∙ 46
23 ∙ 50 + 24 ∙ 4 = 23 ∙ (50 + 4) = 23 ∙ 54
46 ∙ 30 + 46 ∙ 2 = 46 ∙ (30 + 2) = 46 ∙ 32
54 ∙ 20 + 54 ∙ 3 = 54 ∙ (20 + 3) = 54 ∙ 23
Оформляем задание в тетрадь.
32 ∙ 40 + 32 ∙ 6 = 32 ∙ 46
23 ∙ 50 + 23 ∙ 4 = 23 ∙ 54
46 ∙ 30 + 46 ∙ 2 = 46 ∙ 32
54 ∙ 20 + 54 ∙ 3 = 54 ∙ 23
32 ∙ 40 + 32 ∙ 6 = 46 ∙ 30 + 46 ∙ 2
23 ∙ 50 + 23 ∙ 4 = 54 ∙ 20 + 54 ∙ 3
23 ∙ 54 = 54 ∙ 23
32 ∙ 46 = 46 ∙ 32
Номер 11.
Составь по задачам уравнения и реши их.
1) Какое число надо умножить на 4, чтобы получить разность чисел 350 и 70?
2) На какое число надо разделить 750, чтобы получить сумму чисел 32 и 18?
1) х ∙ 4 = 350 − 70
х ∙ 4 = 280
х = 280 : 4
x = 70
70 ∙ 4 = 350 − 70
280 = 280
Ответ: х = 70.
2) 750 : х = 32 + 18
750 : х = 50
х = 750 : 50
x = 15
750 : 15 = 32 + 18
50 = 50
Ответ: х = 15.
Повтори, как решать уравнения.
Выполняем вычисления с пояснениями.
В каждом из составленных уравнений сначала выполняем вычисления в правой части.
1. Чтобы найти первый множитель, нужно произведение разделить на второй множитель:
280 : 4 = 70.
Проверка:
70 ∙ 4 = 350 – 70
280 = 280
2. Чтобы найти делитель, нужно делимое разделить на частное:
750 : 15 = 15.
Проверка:
750 : 15 = 32 + 18
50 = 50
Оформляем задание в тетрадь.
1) х ∙ 4 = 350 − 70
х ∙ 4 = 280
х = 280 : 4
x = 70
Проверка:
70 ∙ 4 = 350 − 70
280 = 280
Ответ: х = 70.
2) 750 : х = 32 + 18
750 : х = 50
х = 750 : 50
x = 15
Проверка:
750 : 15 = 32 + 18
50 = 50
Ответ: х = 15.
Задание на полях страницы
Занимательная рамка.
Ответ:
Проверка:
80 + 120 + 50 = 130 + 120 = 250
80 + 140 + 30 = 140 + 110 = 250
30 + 210 + 10 = 210 + 40 = 250
50 + 190 + 10 = 50 + 200 = 250
В занимательных рамках сумма всех чисел на каждой стороне должна равняться числу в центре.
Выполним вычисления с пояснениями.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известные слагаемые.
250 – (50 + 10) = 250 – 60 = 190
250 – (80 + 50) = 250 – 130 = 120
250 – (30 + 10) = 250 – 40 = 210
250 – (80 + 30) = 250 – 110 = 140
250 – (50 + 10) = 250 – 60 = 190
Оформим задание в тетрадь.
Ребус.
-1.jpg "Изображение математика 4 класс Моро, Бантова - 2 часть страница 54, задание на полях страницы, ребус")
Ответ:
Перед нами ребус, для того чтобы найти недостающие цифры необходимо выполнить деление.
Рассмотрим ребус.
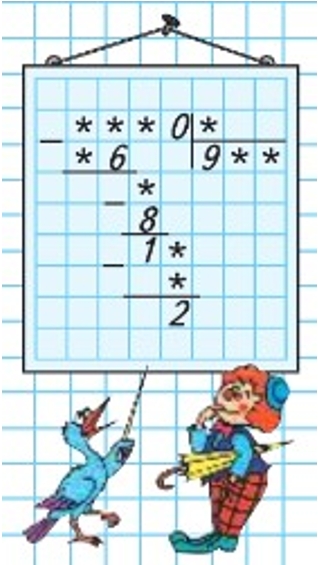
Разгадаем ребус.
Какое двузначное число с цифрой 6 в единицах делится на однозначное число без остатка и в частном получается 9?
Это число 36. Значит, делитель будет 4, так как 36 : 9 = 4.
Далее делили однозначное число, смогли поделить 8 единиц и в остатке получилось 1. Значит, делили число 9. 9 : 4 = 2 (ост. 1).
Какое двузначное число разделили на 4 и получили 2 в остатке? Это число 8. 8 : 4 = 2.
Оформим задание в тетрадь.
Странички для любознательных
Номер 1.
Площадь какой рамки больше?
Найдем площади рамок и узнаем какая больше. 1) Ширина первой рамки - 6 клеток = 3 см Длина первой рамки - 8 клеток = 4 см Площадь рамки с картиной = 3 см ∙ 4 см = 12 см² Найдем площадь картины: Ширина - 1 см Длина - 2 см Площадь картины = 1 см ∙ 2 см = 2 см² Площадь рамки = 12 см² − 2 см² = 10 см² 2) Представим, что восьмиугольную рамку дополнили до квадрата со стороной 4 см. Для этого бы потребовалось найти 4 треугольника, которые вместе образуют два квадрата. Площадь одного такого квадрат 1 см², а двух 2 см². Поэтому площадь картины с рамкой = 4 ∙ 4 - 2 см² = 16 см² − 2 см² = 14 см². Теперь найдем площадь картины. Она равна: 2 см ∙ 2 см = 4 см² - площадь картины. Найдем площадь рамки: 14 см² − 4 см² = 10 см² 10 см² = 10 см², а это значит, что площади рамок картин равны.
Номер 2.
Начерти в тетради квадрат со стороной 3 см и нарисуй в нём кружки так, как расположены собаки на рисунке. Начерти ещё один квадрат так, чтобы каждая собака оказалась отгороженной от других.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽
Напишите свой комментарий.