Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 51

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 198.
Выполни умножение с объяснением.
Ответ:
1) 351 ∙ 18
Умножу первый множитель на число единиц:
351 ∙ 8 = 294
Получу первое неполное произведение 2808.
Умножу первый множитель на число десятков:
351 ∙ 1 = 351
Получу второе неполное произведение: 351.
Начну подписывать второе неполное произведение под десятками.
Сложу неполные произведения.
Читаю ответ: произведение чисел 351 и 18 равно 6318.
2) 708 ∙ 430
Запишу второй множитель так, чтобы десятки второго множителя были под единицами первого множителя (нуль не участвует в умножении).
Умножу первый множитель на число десятков:
708 ∙ 3 = 2124
Получу первое неполное произведение 2124.
Умножу первый множитель на число сотен:
708 ∙ 4 = 2832
Получу второе неполное произведение: 2832.
Начну подписывать второе неполное произведение под сотнями второго множителя.
Сложу неполные произведения, не забыв приписать 0.
Читаю ответ: произведение чисел 708 и 430 равно 304440.
3) 50690 ∙ 16
Запишу второй множитель так, чтобы единицы второго множителя были под десятками первого множителя (нуль не участвует в умножении).
Умножу первый множитель на число единиц:
5069 ∙ 6 = 30414
Получу первое неполное произведение 30414.
Умножу первый множитель на число десятков:
5069 ∙ 1 = 5069
Получу второе неполное произведение: 5069.
Начну подписывать второе неполное произведение под десятками.
Сложу неполные произведения.
Читаю ответ: произведение чисел 50690 и 16 равно 811040.
4) 801 ∙ 401
Умножу первый множитель на число единиц:
801 ∙ 1 = 801
Получу первое неполное произведение 801.
Умножу первый множитель на число сотен, потому что число десятков в обоих множителях равно нулю. При этом неполное произведение буду записывать под сотнями:
801 ∙ 4 = 3204
Получу второе неполное произведение: 3204.
Начну подписывать второе неполное произведение под сотнями.
Сложу неполные произведения.
Читаю ответ: произведение чисел 801 и 401 равно 321201.
Повтори алгоритм письменного умножения на двузначное и трёхзначное числа.
Выполним вычисления.

Объясним, как выполнены вычисления.
1) 351 ∙ 18
Умножу первый множитель на число единиц:
351 ∙ 8 = 294
Получу первое неполное произведение 2808.
Умножу первый множитель на число десятков:
351 ∙ 1 = 351
Получу второе неполное произведение: 351.
Начну подписывать второе неполное произведение под десятками.
Сложу неполные произведения.
Читаю ответ: произведение чисел 351 и 18 равно 6318.
2) 708 ∙ 430
Запишу второй множитель так, чтобы десятки второго множителя были под единицами первого множителя (нуль не участвует в умножении).
Умножу первый множитель на число десятков:
708 ∙ 3 = 2124
Получу первое неполное произведение 2124.
Умножу первый множитель на число сотен:
708 ∙ 4 = 2832
Получу второе неполное произведение: 2832.
Начну подписывать второе неполное произведение под сотнями второго множителя.
Сложу неполные произведения, не забыв приписать 0.
Читаю ответ: произведение чисел 708 и 430 равно 304440.
3) 50690 ∙ 16
Запишу второй множитель так, чтобы единицы второго множителя были под десятками первого множителя (нуль не участвует в умножении).
Умножу первый множитель на число единиц:
5069 ∙ 6 = 30414
Получу первое неполное произведение 30414.
Умножу первый множитель на число десятков:
5069 ∙ 1 = 5069
Получу второе неполное произведение: 5069.
Начну подписывать второе неполное произведение под десятками.
Сложу неполные произведения.
Читаю ответ: произведение чисел 50690 и 16 равно 811040.
4) 801 ∙ 401
Умножу первый множитель на число единиц:
801 ∙ 1 = 801
Получу первое неполное произведение 801.
Умножу первый множитель на число сотен, потому что число десятков в обоих множителях равно нулю. При этом неполное произведение буду записывать под сотнями:
801 ∙ 4 = 3204
Получу второе неполное произведение: 3204.
Начну подписывать второе неполное произведение под сотнями.
Сложу неполные произведения.
Читаю ответ: произведение чисел 801 и 401 равно 321201.
Номер 199.
Ответ:
Повтори алгоритм письменного умножения на двузначное число, а также порядок действий.
Выполним вычисления с пояснениями.

Пишу: 156 ∙ 82.
Умножу первый множитель на число единиц:
156 ∙ 2 = 312.
Получу первое неполное произведение: 312.
Умножу первый множитель на число десятков:
156 ∙ 8 = 1 248.
Получу второе неполное произведение: 1 248 дес.
Начну подписывать второе неполное произведение под десятками.
Сложу неполные произведения.
Читаю ответ: 12 792. Это произведение чисел 156 и 82.
Пишу: 40 136 ∙ 21.
Умножу первый множитель на число единиц:
40 136 ∙ 1 = 40 136.
Получу первое неполное произведение: 40 136.
Умножу первый множитель на число десятков:
40 136 ∙ 2 = 80 272.
Получу второе неполное произведение: 80 272 дес.
Начну подписывать второе неполное произведение под десятками.
Сложу неполные произведения.
Читаю ответ: 842 856. Это произведение чисел 40 136 и 21.
Оформим задание в тетрадь.
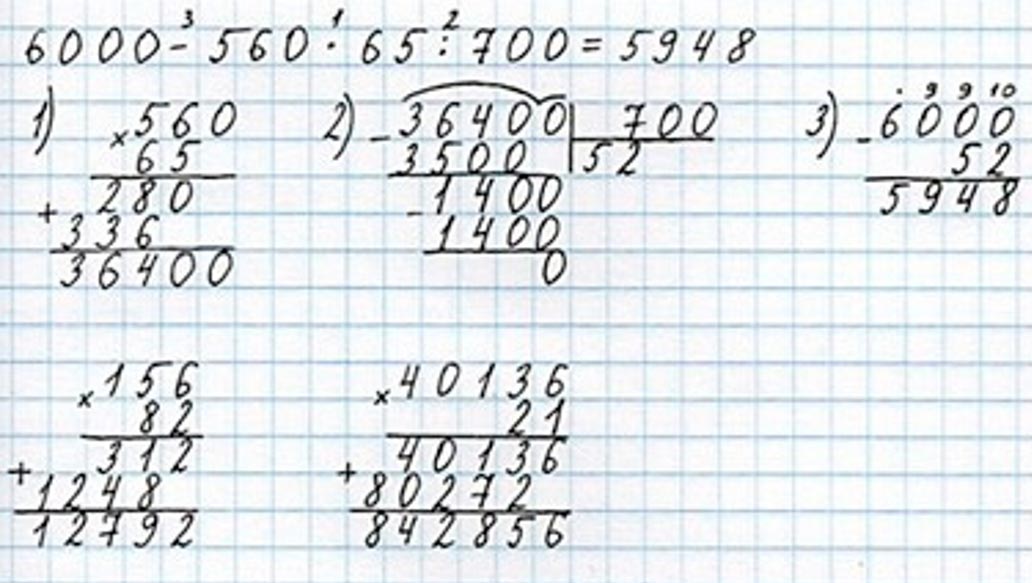
Номер 200.
Реши задачи. Сравни задачи, сравни их решения.
1) На двух опытных участках вырастили картофель. Площадь первого участка 200 м², а второго 300 м². С первого участка собрали на 1500 кг картофеля меньше, чем со второго. Сколько килограммов картофеля собрали с каждого участка, если с каждого квадратного метра собирали поровну?
2) С двух опытных участков собрали 7500 кг картофеля. Площадь первого участка 200 м², а второго 300 м². С каждого квадратного метра собирали картофеля поровну. Сколько килограммов картофеля собрали с каждого участка?
Задача 1:

1) 300 − 200 = 100 (м²) – разница площадей участков.
2) 1500 : 100 = 15 (кг) – картофеля собирают с 1 м².
3) 15 ∙ 200 = 3000 (кг) – картофеля собрали с 1ого участка.
4) 15 ∙ 300 = 4500 (кг) – картофеля собрали со 2ого участка.
Ответ: 3000 кг картофеля собрали с первого участка и 4500 кг картофеля всего собрали со второго участка.
Задача 2:
.jpg)
1) 200 + 300 = 500 (м²) – площадь участков.
2) 7500 : 500 = 15 (кг) – картофеля собрали с 1 м².
3) 15 ∙ 200 = 3000 (кг) – картофеля собрали с первого участка.
4) 15 ∙ 300 = 4500 (кг) – картофеля собрали со второго участка.
Ответ: 3000 кг картофеля всего собрали с первого участка и 4500 кг картофеля собрали со второго участка.
Сравнение:
Задачи похожи. Мы знаем и в той и в другой площади участков, а также в обеих задачах просят найти сколько картофеля собрали с каждого участка.
Но есть и отличия. В первой задачи нам нужно сначала узанать на сколько площадь одного участка больше площади другого участка, чтобы узнать расход на 1 м², а во второй сложить их и поделить масса картофеля на полученное число, чтобы тоже найти количество картофеля, собранного с 1 м².
А затем полученное значение - 15м² - мы умножаем на площади участков и находим, сколько картофеля собрали с одного и с другого участка.
Повтори единицу массы – килограмм и единицы площади.
Шаг 1.
Оформляем условие в виде таблицы.

Рассуждаем.
Вычислим разницу между площадями участков.
1) 300 − 200 = 100 (м²) – разница площадей участков.
Продолжаем рассуждение.
Нам известна разница между площадями участка и между количеством картофеля, вычислим, сколько кг картофеля собирают с 1 м².
2) 1500 : 100 = 15 (кг) – картофеля собирают с 1 м².
Продолжаем рассуждение.
Узнаем, сколько кг картофеля собрали с 1-го участка.
3) 15 ∙ 200 = 3000 (кг) – картофеля собрали с 1-го участка.
Продолжаем рассуждение.
Узнаем, сколько кг картофеля собрали со 2-го участка.
4) 15 ∙ 300 = 4500 (кг) – картофеля собрали со 2-го участка.
Записываем ответ.
Ответ: 3000 кг и 4500 кг.
Шаг 1.
Оформляем условие в виде таблицы.

Рассуждаем.
Вычислим общую площадь двух участков.
1) 200 + 300 = 500 (м²) – площадь участков.
Продолжаем рассуждение.
Нам известно, сколько картофеля собрали с двух опытных участков, а также их общая площадь. Вычислим, сколько килограммов картофеля собирают с 1 м².
2) 7500 : 500 = 15 (кг) – картофеля собрали с 1 м².
Продолжаем рассуждение.
Узнаем, сколько кг картофеля собрали с 1-го участка.
3) 15 ∙ 200 = 3000 (кг) – карт. собрали с 1-го участка.
Продолжаем рассуждение.
Узнаем, сколько кг картофеля собрали со 2-го участка.
4) 15 ∙ 300 = 4500 (кг) – карт., собрали со 2-го участка.
Записываем ответ.
Ответ: 3000 кг и 4500 кг.
Сравниваем задачи.
Задачи похожи. Мы знаем и в той и в другой площади участков, а также в обеих задачах просят найти, сколько картофеля собрали с каждого участка.
Но есть и отличия. В первой задачи нам нужно сначала узнать, насколько площадь одного участка больше площади другого участка, чтобы узнать расход на 1 м², а во второй сложить их и поделить масса картофеля на полученное число, чтобы тоже найти количество картофеля, собранного с 1 м².
А затем полученное значение – 15м² – мы умножаем на площади участков и находим, сколько картофеля собрали с одного и с другого участка.
Номер 201.
Объясни, что показывает каждое выражение, составленное по следующей таблице:

1) 70 ∙ 3 = 210 (км) – путь, который преодолел первый объект. 2) 65 ∙ 3 = 195 (км) – путь, который преодолел второй объект. 3) 70 + 65 = 135 (км/ч) – скорость сближения или удаления. 4) (70 + 65) ∙ 3 = 405 (км) – расстояние между объектами через 3 часа. 5) 70 − 65 = 5 (км/ч) – на столько первый объект быстрее второго. 6) (70 − 65) ∙ 3 = 15 (км) – на столько первый объект проехал больше, чем второй объект.
Повтори взаимосвязь между скоростью, временем и расстоянием.
Рассмотрим таблицу в учебнике.

Объясним, что означает каждое из данных выражений.
1) 70 ∙ 3 = 210 (км) – путь, который преодолел первый объект.
2) 65 ∙ 3 = 195 (км) – путь, который преодолел второй объект.
3) 70 + 65 = 135 (км/ч) – скорость сближения или удаления.
4) (70 + 65) ∙ 3 = 405 (км) – расстояние между объектами через 3 часа.
5) 70 − 65 = 5 (км/ч) – на столько первый объект быстрее второго.
6) (70 − 65) ∙ 3 = 15 (км) – на столько первый объект проехал больше, чем второй объект.
Оформим задание в тетрадь.
Номер 202.
1) Первый множитель 127, он на 27 больше второго множителя. Найди произведение этих чисел.
2) Делимое 5600, а делитель на 4900 меньше. Найди частное.
1) 127 ∙ (127 − 27) = 127 ∙ 100 = 12700 2) 5600 : (5600 − 4900) = 5600 : 700 = 8
Повтори, как называются числа при умножении и делении.
Выполним вычисления по действиям.
127 ∙ (127 – 27) = 12 700
1) 127 – 27 = 100
2) 127 ∙ 100 = 12 700
5 600 : (5 600 – 4 900) = 8

2) 5 600 : 700 = 8
Оформим задание в тетрадь.
1) 127 ∙ (127 − 27) = 127 ∙ 100 = 12700
2) 5600 : (5600 − 4900) = 5600 : 700 = 8
Номер 203.
Вырежи квадрат со стороной 12 см. Раздели его перегибанием на четыре равных треугольника и найди площадь каждого из них.
Ответ:
1) 12 ∙ 12 = 144 (см²) – площадь квадрата.
2) 144 : 4 = 36 (см²) - площадь одного треугольника.
Ответ: 36 см² площадь одного треугольника.
Повтори, как найти площадь квадрата.
Начертим и вырежем квадрат.
С помощью перегибания разделим его на 4 равных треугольника.
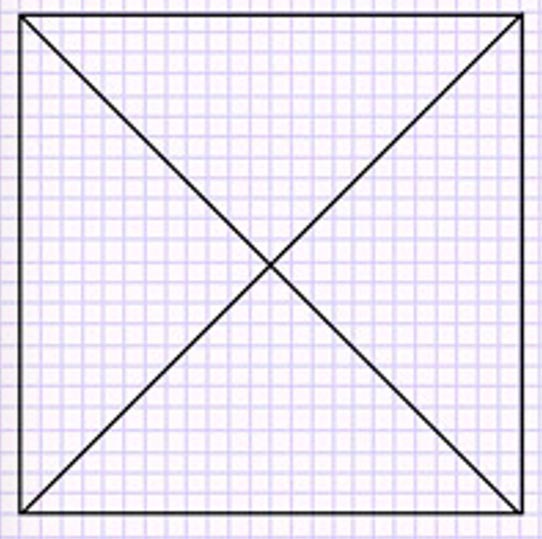
Найдем площадь квадрата и каждого треугольника.
Площадь квадрата можно определить, умножив сторону саму на себя.
1) 12 ∙ 12 = 144 (см²) – площадь квадрата.
Найдем площадь каждого треугольника.
Квадрат разделили на 4 равных треугольника, значит, площадь каждого из них в 4 раза меньше площади квадрата.
2) 144 : 4 = 36 (см²) – площадь одного треугольника.
Записываем ответ.
Ответ: 36 см².
Номер 204.
Вырази:
1) в метрах: 5 км, 900 дм, 300 см;
2) в килограммах: 9 т, 6 т 5 ц, 800 ц, 4000 г;
3) в секундах: 2 мин, 1 мин 30 с, 2 мин 30 с;
4) в квадратных метрах: 300 дм², 80000 см², 9 км².
1) 5 км = 5000 м; 900 дм = 90 м; 300 см = 3 м. 2) 9 т = 9000 кг; 6 т 5 ц = 6500 кг; 800 ц = 80000 кг; 4000 г = 4 кг. 3) 2 мин = 120 с; 1 мин 30 с. = 90 с; 2 мин 30 с. = 150 с. 4) 300 дм² = 3 м²; 80000 см² = 8 м²; 9 км² = 9000000 м².
Повтори меры длины – километр, метр, дециметр и сантиметр, единицы массы – тонну, центнер, килограмм и грамм, единицы времени – минуту и секунду, а также единицы площади.
Выразим данные значения в метрах.
5 км = 5000 м; 900 дм = 90 м; 300 см = 3 м.
Выразим данные значения в килограммах.
9 т = 9000 кг; 6 т 5 ц = 6500 кг; 800 ц = 80000 кг; 4000 г = 4 кг.
Выразим данные значения в секундах.
2 мин = 120 с; 1 мин 30 с. = 90 с; 2 мин 30 с. = 150 с.
Выразим данные значения в квадратных метрах.
300 дм² = 3 м²; 80000 см² = 8 м²; 9 км² = 9000000 м².
Задание внизу страницы
Ответ:
Повтори алгоритм письменного умножения и деления на двузначное число, сложения многозначных чисел, а также порядок действий.
Выполняем вычисления с пояснениями.
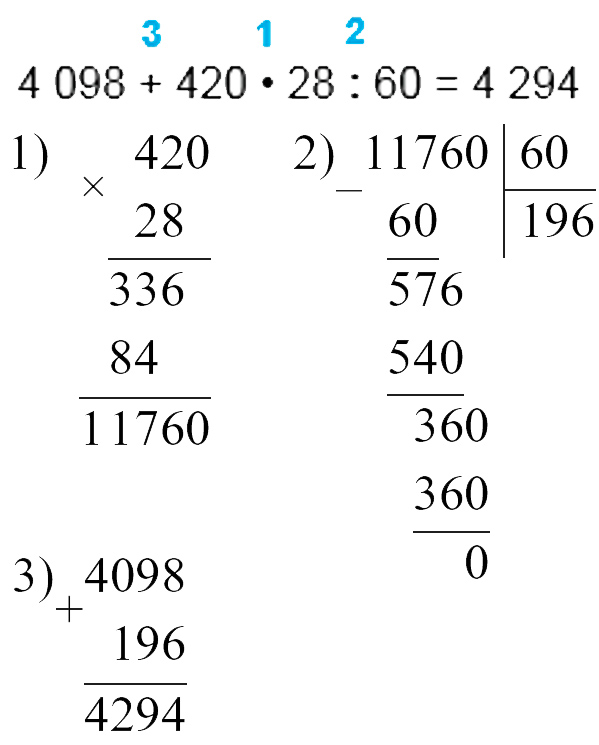
Пишу: 709 ∙ 19.
Умножу первый множитель на число единиц:
709 ∙ 9 = 6 381.
Получу первое неполное произведение: 6 381.
Умножу первый множитель на число десятков:
709 ∙ 1 = 709.
Получу второе неполное произведение: 709 дес.
Начну подписывать второе неполное произведение под десятками.
Сложу неполные произведения.
Читаю ответ: 13 471. Это произведение чисел 709 и 19.
Пишу: 52 070 ∙ 14.
Ноль смещаем вправо и не учитываем его в умножении.
Умножу первый множитель на число единиц:
5 207 ∙ 4 = 20 828.
Получу первое неполное произведение: 20 828.
Умножу первый множитель на число десятков:
5207 ∙ 1 = 5207.
Получу второе неполное произведение: 5207 дес.
Начну подписывать второе неполное произведение под десятками.
Сложу неполные произведения. Допишу к ответу справа ноль из второго множителя.
Читаю ответ: 728 980. Это произведение чисел 52 070 и 14.
Оформляем задание в тетрадь.
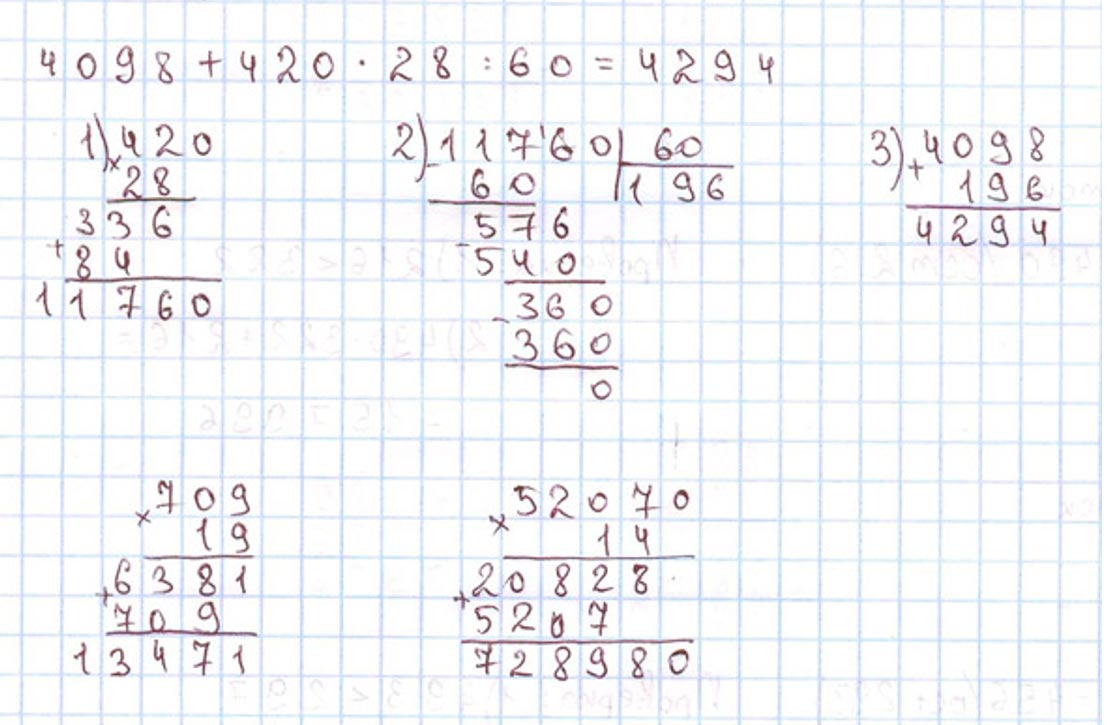
Задание на полях страницы
Реши. Найди лишнее уравнение.

Ответ:
х : 16 = 6
х = 16 ∙ 6
х = 96
Проверка:
96 : 16 = 6
6 = 6
Ответ: х = 96
х : 24 = 4
х = 24 ∙ 4
х = 96
Проверка:
96 : 24 = 4
4 = 4
Ответ: х = 96
х : 36 = 2
х = 36 ∙ 2
х = 72
Проверка:
72 : 36 = 2
2 = 2
Ответ: х = 72
х : 48 = 2
х = 48 ∙ 2
х = 96
Проверка:
96 : 48 = 2
2 = 2
Ответ: х = 96
Лишнее уравнение х : 36 = 2.
Повтори, как решать уравнения.
Выполняем вычисления.
х : 16 = 6
х = 6 ∙ 16
х = 96
х : 24 = 4
х = 4 ∙ 24
х = 96
х : 36 = 3
х = 3 ∙ 36
х = 108
х : 48 = 2
х = 2 ∙ 48
х = 96
Лишнее уравнение х : 36 = 2.
Оформляем задание в тетрадь.
Ребус.

Ответ:

Повтори, как называются числа при сложении, вычитании и делении.
Рассмотрим примеры.
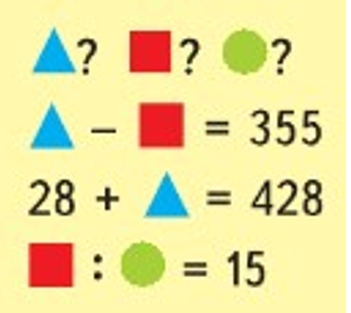
Выполним вычисления.
1) 428 – 28 = 400 – значение синего треугольника.
2) 400 – 355 = 45 – значение красного квадрата.
3) 45 : 15 = 3 – значение зеленого круга.
Оформим задание в тетрадь.

Задание вверху страницы
Рассмотри и сравни, как выполнено умножение.

Умножение трехзначного числа на трехзначное с нулем на месте десятков выполняют следующим образом: умножают первый множитель на количество единиц, умножение на количество десятков пропускается, потому что второе произведение равно 0, а третье произведение записывают под сотнями. Два неполных произведения (по сути три, но второе равно 0) складывают и записывают ответ. Умножение трехзначного числа на трехзначное число с нулем на конце выполняют немного по-другому. Второй множитель с нулем на конце записывают со сдвигом влево на 1 знак, так что нуль не участвует в умножении. Это делается для того, чтобы сократить лишнюю работу и не записывать целую строку нулей, как результат умножения первого множителя на количество единиц. Далее выполняются умножения на количество десятков, сотен, результаты записываются со сдвигом влево и затем складываются, а нуль на конце приписывают. Проще говоря, при умножении трехзначного числа на трехзначное число с нулем на конце пропускается действие умножение первого множителя на количество единиц, потому что количество единиц в таком числе равно нулю.
Назови каждое неполное произведение.
Ответ:При умножении 327 на 406 получаются три неполных произведения:1962, 0 и 1308. При умножении 614 на 280 получаются три неполных произведения: 4912, 0 и 1228. Но для того, чтобы сократить работу первое неполное произведение не прописывают и не ищут его, так как нуль сдвинут и не участвует в умножении.
Объясни, почему в таких случаях при умножении на трехзначное число записывают только два неполных произведения и как их подписывают.
Ответ:При умножении трехзначного числа на трехзначное число с нулем на позиции десятков, получается три неполных произведения. Первое записывается под единицами, второе не записывается, но мысленно мы помним, что оно записывается под десятками, а третье неполное произведение записываем под сотнями. Складываем неполные произведения и читаем ответ. Также есть особенность при умножении трехзначного числа на трехзначное число с нулем на позиции единиц. Второй множитель записывают со сдвигом влево на 1 знак и поэтому число, означающее десятки становится условно единицами, а сотни - десятками. У нас получаются всего два неполных произведения, потому что умножение на нуль не выполняют и первым неполным произведением, записываемым под единицами, становится уже число, полученное при умножении первого множителя на количество десятков. При умножении на количество сотен записывают результат под десятками.
Номер 200.
Вычисли с объяснением.
Ответ:
1) 254 ∙ 37
Умножу первый множитель на число единиц:
254 ∙ 7 = 1778
Получу первое неполное произведение 1778.
Умножу первый множитель на число десятков:
254 ∙ 3 = 762
Получу второе неполное произведение: 762.
Начну подписывать второе неполное произведение под десятками.
Сложу неполные произведения.
Читаю ответ: произведение чисел 254 и 37 равно 9398.
2) 254 ∙ 307
Умножу первый множитель на число единиц:
254 ∙ 7 = 1778
Получу первое неполное произведение 1778.
Умножу первый множитель на число десятков:
254 ∙ 0 = 0
Получу второе неполное произведение: 0.
Умножу первый множитель на число сотен:
254 ∙ 3 = 762
Получу третье неполное произведение: 762.
Начну подписывать второе неполное произведение под десятками, а третье под сотнями.
Сложу неполные произведения.
Читаю ответ: произведение чисел 254 и 307 равно 77978.
3) 481 ∙ 360
Записываем второй множитель со сдвигом вправо на 1 знак и таким образом первым действием выполняем умножение первого множителя на количество десятков.
Умножу первый множитель на число десятков:
481 ∙ 6 = 2886
Получу первое неполное произведение 2886.
Умножу первый множитель на число сотен:
481 ∙ 3 = 1443
Получу второе неполное произведение: 1443.
Начну подписывать первое неполное произведение под единицами, а второе неполное произведение под сотнями. Нуль припысываю к ответу справа.
Сложу неполные произведения.
Читаю ответ: произведение чисел 481 и 306 равно 173160.
Номер 201.
Ответ:

Номер 202.
Двум классам поручено расчистить школьный каток, длины которого 20 м, а ширина 10 м. В одном классе 26 учеников, а в другом 24. Сколько квадратных метров должен расчистить каждый класс, если распределить работу по числу учеников?
Ответ:
1) 20 ∙ 10 = 200 (м²) – площадь катка.
2) 26 + 24 = 50 (уч.) – в двух классах всего.
3) 200 : 50 = 4 (м²) – должен расчистиить один ученик.
4) 4 ∙ 26 = 104 (м²) – должны расчистить ученики первого класса.
5) 4 ∙ 24 = 96 (м²) – должны расчистить ученики второго класса.
Ответ: 104 м² должны расчистить ученики первого класса и 96 м² должны расчистить ученики второго класса.
Номер 203.
У фермера 4 лошади и 9 коров. Лошади требуется на месяц 135 кг сена, а трём коровам – столько сена, сколько необходимо семи лошадям. Сколько килограммов сена должен расходовать фермер ежемесячно на всех лошадей и коров?
Ответ:4 лошади и 9 коров = ? кг сена всего 1 лошадь = 135 кг сена 3 коровы = 7 лошадей = ? кг сена
1) 135 ∙ 7 = 945 (кг) – сена нужно для 3 коров.

2) 9 : 3 = 3 (р.) – 9 коров больше в 3 раза, чем 3 коровы. 3) 945 ∙ 3 = 2835 (кг) – сена нужно для 9 коров.

4) 135 ∙ 4 = 540 (кг) – сена нужно для 4 лошадей.

5) 2835 + 540 = 3375 (кг) - должен расходовать фермер каждый месяц


Ответ: 3375 кг сена должен расходовать фермер ежемесячно на всех лошадей и коров.
Номер 204.
Высота футбольных ворот 2 м 40 см, она в 2 раза больше высоты хоккейных ворот. Узнай высоту хоккейных ворот.
Ответ:
2 м 40 см = 240 см
240 : 2 = 120 (см) – высота хоккейных ворот.
Ответ: высота хоккейных ворот составляет 1 м 20 см.
Номер 205.
1) Начерти отрезок длиной 8 см. Раздели его на 2 равные части. Какие доли отрезка получились? Сколько их? Раздели каждую половину ещё на 2 равные части. Какие доли отрезка получились? Сколько их в целом отрезке? Сколько четвёртых долей отрезка в его половине?
2) Раздели каждую четвёртую долю отрезка на 2 равные части. Какие доли отрезка получились? Сколько восьмых долей в трёх четвёртых отрезка?
Если разделить отрезок на 2 равные части, то получается две доли, которые можно назвать половина или одна вторая.

Разобъём каждую половину пополам. Получились 4 доли, которые называют четвёртые доли или одна четвёртая или четвертина.
.jpg)
Разобъём каждую четвёртую часть пополам. Получились 8 равных долей. Их называют восьмые доли или одна восьмая часть.
.jpg)
В трёх четвёртых отрезка шесть восьмых долей.
Задание внизу страницы
Ответ:
Задание на полях страницы
Сравни площади фигур.

Ответ:

Площади всех фигур одинаковые, потому что если мы разобьем квадрат на 2 треугольника, то увидим, что эти треугольники, равны треугольникам, из которых составлены фигуры 2 и 3, а это значит, что все фигуры равны.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.