Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 35

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Что узнали. Чему научились
Номер 1.
Ответ:
84 ∙ 10 − 40 = 840 − 40 = 800
78 ∙ 10 − 700 = 780 − 700 = 80
10 ∙ (920 − 20) = 10 ∙ 900 = 9000
8 ∙ (720 − 700) = 8 ∙ 20 = 160
184 ∙ 100 − 300 = 18400 − 300 = 18100
100 ∙ 391 − 3000 = 39100 − 3000 = 36100
Повтори алгоритм умножения на круглое число и порядок действий.
Выполняем вычисления по действиям.
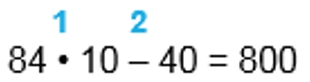
1) 84 ∙ 10 = 840
2) 840 – 40 = 800
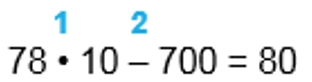
1) 78 ∙ 10 = 780
2) 780 – 700 = 80
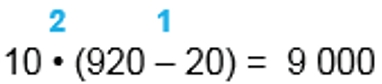
1) 920 – 20 = 900
2) 10 ∙ 900 = 9 000
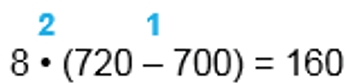
1) 720 – 700 = 20
2) 8 ∙ 20 = 160
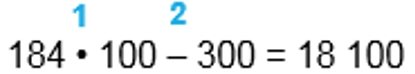
1) 184 ∙ 100 = 18 400
2) 18 400 – 300 = 18 100
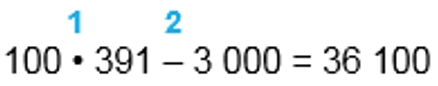
1) 100 ∙ 391 = 39 100
2) 39 100 – 3 000 = 36 100
Оформляем задание в тетрадь.
84 ∙ 10 − 40 = 840 − 40 = 800
78 ∙ 10 − 700 = 780 − 700 = 80
10 ∙ (920 − 20) = 10 ∙ 900 = 9000
8 ∙ (720 − 700) = 8 ∙ 20 = 160
184 ∙ 100 − 300 = 18400 − 300 = 18100
100 ∙ 391 − 3000 = 39100 − 3000 = 36100
Номер 2.
Ответ:
Повтори алгоритм умножения на круглое число и порядок действий.
Выполняем вычисления.

1) 50 : 50 = 1
2) 1 ∙ 100 = 100

1) 24 ∙ 10 = 240
2) 240 : 8 = 30
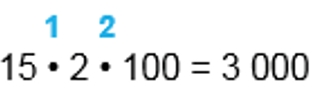
1) 15 ∙ 2 = 30
2) 30 ∙ 100 = 3 000
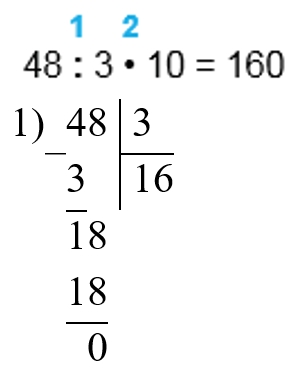
2) 16 ∙ 10 = 160
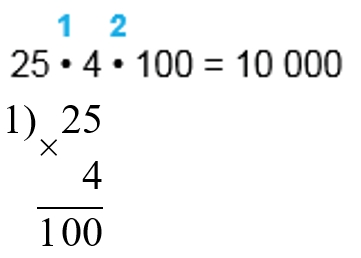
2) 100 ∙ 100 = 10 000

1) 100 : 2 = 50
2) 50 : 10 = 5
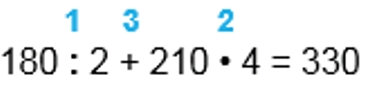
1) 180 : 2 = 90
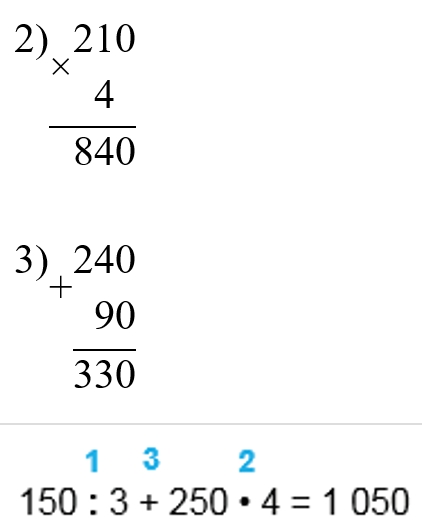
1) 150 : 3 = 50
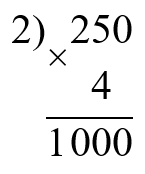
3) 50 + 1 000 = 1 050
Оформляем задание в тетрадь.
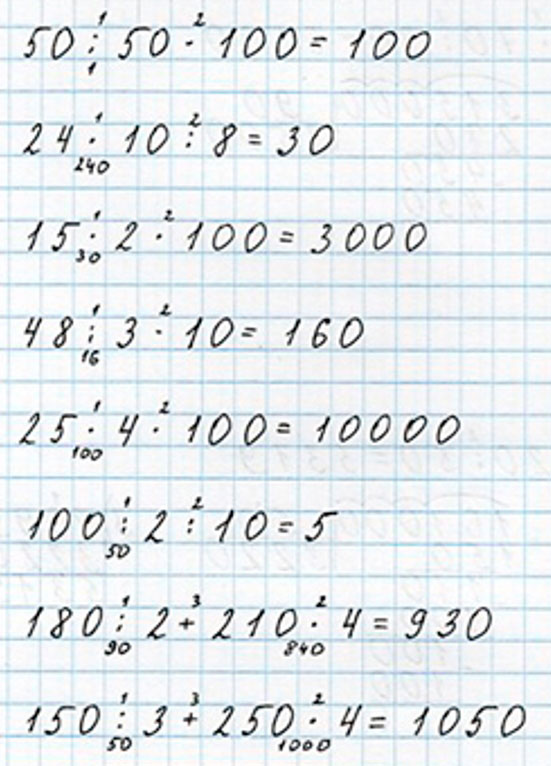
Номер 3.
Ответ:
Помним алгоритм объяснения умножения трехзначного числа на однозначное:
1) Записываю первый множитель так, чтобы каждая цифра стояла в своей клетке. Ставлю знак умножить.
2) Записываю второй множитель так, чтобы разряд стоял под разрядом.
3) Провожу черту, обозначающую знак равно.
4) Умножение начинаю с единиц низшего разряда.
5) Умножаю десятки.
6) Умножаю сотни.
7) Умножение окончено. Читаю ответ.
Выполняем вычисления с пояснениями.
Пишу (единицы под единицами, десятки под десятками, сотни под сотнями): 107 ∙ 7.
Умножаю единицы: 7 ∙ 7 = 49. 49 ед. – это 4 дес. и 9 ед., 9 ед. пишу под десятками, а 4 дес. запомню и прибавлю к десяткам после умножения единиц.
Умножаю десятки: 0 ∙ 7 = 0. К 0 дес. прибавляю 4 дес., которые получены при умножении единиц: 0 + 4 = 4. Пишу 4 под десятками.
Умножаю сотни: 1 ∙ 7 = 7. Пишу 7 под сотнями.
Читаю ответ: 749.
Далее рассуждаю аналогично.
Выполняем вычисления и оформляем задание в тетрадь.
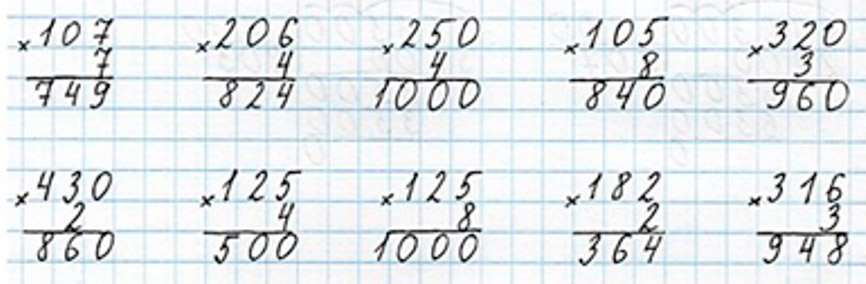
Номер 4.
Выполни деление с остатком.
Ответ:
Алгоритм деления примеров с остатком.
1) Находим наибольшее число до делимого, которое можно разделить на делитель без остатка.
2) Данное число делим на делитель. Это значение частного.
3) Вычитаем из делимого наибольшее число – это остаток.
4) Проверяем, остаток должен быть меньше делителя.
5) Делаем проверку.
Выполняем вычисления с пояснениями.
327 : 10.
Без остатка 327 на 10 не разделится.
Разделим 320 на 10. Получим 32. Это – частное, а остаток 7. Записываем так:
327 : 10 = 32 (ост. 7)
1 684 : 100.
Без остатка 1 684 на 100 не разделится.
Разделим 1600 на 100. Получим 16. Это – частное, а остаток 84. Записываем так:
1 684 : 100 = 16 (ост. 84)
Далее рассуждаем аналогично.
Выполняем вычисления и оформляем задание в тетрадь.
327 : 10 = 32 (ост. 7)
358 : 10 = 35 (ост. 8)
615 : 100 = 6 (ост. 15)
1 684 : 100 = 16 (ост. 84)
1 605 : 10 = 160 (ост. 5)
1 730 : 100 = 17 (ост. 30)
15 928 : 100 = 159 (ост. 28)
15 862 : 10 = 1 586 (ост. 2)
34 518 : 100 = 345 (ост. 18)
135 628 : 10 = 13 562 (ост. 8)
36 704 : 10 = 3 670 (ост. 4)
52 080 : 100 = 520 (ост. 80)
Номер 5.
Вычисли удобным способом.
Ответ:45 ∙ (2 ∙ 7) = (45 ∙ 2) ∙ 7 = 90 ∙ 7 = 630 720 : (9 ∙ 2) = (720 : 9) : 2 = 80 : 2 = 40 67 ∙ (4 ∙ 25) = 67 ∙ 100 = 6700 17 ∙ 2 ∙ 8 ∙ 125 = 34 ∙ 1000 = 34000
Помним о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Выполняем вычисления с пояснением.
45 ∙ (2 ∙ 7) = (45 ∙ 2) ∙ 7 = 90 ∙ 7 = 630
720 : (9 ∙ 2) = (720 : 9) : 2 = 80 : 2 = 40
67 ∙ (4 ∙ 25) = 67 ∙ 100 = 6 700
17 ∙ 2 ∙ 8 ∙ 125 = (17 ∙ 2) ∙ (8 ∙ 125) = 34 ∙ 1 000 = 34 000
Группируем множители так, чтобы последним действием умножать на круглое число.
Оформляем задание в тетрадь.
45 ∙ (2 ∙ 7) = (45 ∙ 2) ∙ 7 = 90 ∙ 7 = 630
720 : (9 ∙ 2) = (720 : 9) : 2 = 80 : 2 = 40
67 ∙ (4 ∙ 25) = 67 ∙ 100 = 6 700
17 ∙ 2 ∙ 8 ∙ 125 = 34 ∙ 1000 = 34 000
Номер 6.
Ответ:
Повтори алгоритм умножения на круглое число.
Выполняем вычисления с пояснениями.
Пишу: 213 ∙ 90.
213 ∙ 90 – это число 213, которые умножили на 9 дес., поэтому умножим 213 на 9, затем допишем к произведению справа ноль.
Умножаю единицы: 3 ∙ 9 = 27. 27 ед. – это 2 дес. и 7 ед., 7 ед. пишу под единицами, а 2 дес. запомню и прибавлю к десяткам после умножения десятков.
Умножаю десятки: 1 ∙ 9 = 9. К 9 дес. прибавляю 2 дес., которые получены при умножении единиц: 9 + 2 = 11. 11 дес. – это 1 сот. и 1 дес., 1 дес. пишу под десятками, а 1 сот. запомню и прибавлю к сотням после умножения сотен.
Умножаю сотни: 2 ∙ 9 = 18. К 18 сот. прибавляю 1 сот., которая получена при умножении десятков: 18 + 1 = 19. 19 сот. – это 1 ед. тыс. и 9 сот., 9 сот. пишу под сотнями, а 1 ед. тыс. пишу в ответ в разряд тысяч, так как других тысяч для умножения нет.
Допишем к произведению справа 1 ноль.
Читаю ответ: 19 170.
Далее рассуждаю аналогично.
Выполняем вычисления и оформляем задание в тетрадь.

Номер 7.
Ответ:
Чтобы найти произведение круглых чисел, надо выполнить умножение, не обращая внимания на нули на конце, а затем в полученном произведении приписать справа столько нулей, сколько их на конце обоих множителей вместе.
Алгоритм:
1) Пишу первый множитель.
2) Второй множитель записываю так, чтобы нули остались в стороне.
3) Правильно умножаю числа, не обращая внимания на нули.
4) Считаю нули и приписываю.
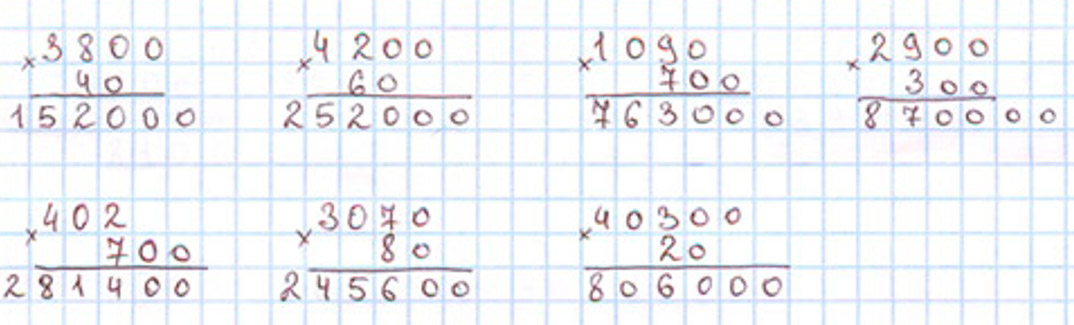
Выполняем вычисления с пояснениями.
Пишу: 580 ∙ 600.
580 ∙ 60 – это 58 дес., которые умножили на 6 сот., поэтому умножим 58 на 6, затем допишем к произведению справа 3 нуля.
Умножаю единицы: 8 ∙ 6 = 48. 48 ед. – это 4 дес. и 8 ед., 8 ед. пишу под единицами, а 4 дес. запомню и прибавлю к десяткам после умножения десятков.
Умножаю десятки: 5 ∙ 6 = 30. К 30 дес. прибавляю 4 дес., которые получены при умножении единиц: 30 + 4 = 34. 34 дес. – это 3 сот. и 4 дес., 4 дес. пишу под десятками, а 3 сот. пишу в ответ в разряд сотен, так как других сотен для умножения нет.
Допишем к произведению справа 3 нуля.
Читаю ответ: 348 000.
Далее рассуждаю аналогично.
Выполняем вычисления и оформляем задание в тетрадь.
Номер 8.
Ответ:
Алгоритм письменного деления на числа, оканчивающиеся нулями:
1. Выделить первое неполное делимое.
2. Определить количество цифр в частном.
3. Разделить неполное делимое на делитель.
4. Умножить делитель на полученное число.
5. Найти остаток от деления вычитанием.
6. Сравнить остаток с делителем.
Выполняем вычисления с пояснениями.
Пишу: 46 800 : 600.
Первое неполное делимое – 4 680 десятков. В записи частного будет 2 цифры.
Разделю 4 680 на 600. Для этого разделю 46 на 6, получу 7 – столько десятков будет в частном.
Умножу 600 на 7, получу 4 200 – столько десятков разделили.
Вычту 4 200 из 4 680, получу 480 – столько десятков осталось разделить.
Сравню остаток с делителем: десятков осталось меньше, чем 600.
Второе неполное делимое – 4 800 единиц.
Разделю 4 800 на 600. Для этого разделю 48 на 6, получу 8 – столько единиц будет в частном.
Умножу 600 на 8, получу 4 800 – все единицы разделили.
Читаю ответ: частное равно 78.
Далее рассуждаю аналогично.
Выполняем вычисления и оформляем задание в тетрадь.

Номер 9.
Ответ:
Помним о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Выполняем вычисления по действиям.

Оформляем задание в тетрадь.
100 520 – 470 ∙ 50 + 13 980 = 91 000
14 110 + 801 000 : 900 – 7 604 = 7 396
734 600 : 50 + 454 ∙ 40 = 32 852
(560 – 12 240 : 30) + 145 = 297
400 000 – 867 ∙ 400 = 53 200
9 805 + 146 510 : 70 = 11 898
8 213 ∙ 30 – 12 240 : 30 = 245 982
11 140 : (2 076 – 2 056) = 557
Номер 10.
Ответ:
Помним о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Выполняем вычисления по действиям.

Оформляем задание в тетрадь.
463 700 : 50 + 546 ∙ 40 = 31 114
55 440 : 90 – 10 460 : 20 = 93
41 090 : 70 + 11 950 : 50 = 826
8 130 : 30 – 2 640 : 10 = 7
900 100 – (735 – 184) ∙ 80 = 856 020
60 997 + (6 012 + 6 228) : 30 = 61 405
Номер 11.
Какими могут быть длины сторон прямоугольника, периметр которого равен 26 см, а площадь – 40 см²?
Ответ:5 см и 8 см.
Длина – величина, характеризующая протяженность объекта на плоскости, выражается в таких единицах измерения, как миллиметр, сантиметр, дециметр, метр, километр.
Помни о соотношении числовых значений единиц измерения длины:
1 см = 10 мм
1 дм = 10 см
1 м = 100 см
1 м = 10 дм
1 км = 1000 м
Оформляем условие в виде таблицы.

Рассуждаем.
У прямоугольника, площадь которого равна 40 см2, произведение длин соседних сторон равно 40. Значит, это могут быть прямоугольники с соседними сторонами:
• 1 см и 40 см
• 2 см и 20 см
• 4 см и 10 см
• 5 см и 8 см
Продолжаем рассуждение.
У прямоугольника, периметр которого равен 26 см, сумма длин соседних сторон равна половине периметра, то есть 13 см. Проверим, какие из прямоугольников площадью 40 см2 удовлетворяют этому условию:
• 1 + 40 ≠ 13 – не подходит;
• 2 + 20 ≠ 13 – не подходит;
• 4 + 10 ≠ 13 – не подходит;
• 5 + 8 = 13 – подходит.
Делаем вывод.
Значит у прямоугольника, периметр которого равен 26 см, а площадь 40 см2, длины соседних сторон равны 5 см и 8 см.
Записываем ответ.
Ответ: 5 см и 8 см.
Номер 12.
Вычислительная машинка работает так:

Какой ответ будет получаться на выходе из машины, если на входе будет число 47; 53; 28; 94?
Ответ:47 − 2; 53 − 2; 28 − 1; 94 − 1.
Алгоритм деления примеров с остатком.
1) Находим наибольшее число до делимого, которое можно разделить на делитель без остатка.
2) Данное число делим на делитель. Это значение частного.
3) Вычитаем из делимого наибольшее число – это остаток.
4) Проверяем, остаток должен быть меньше делителя.
5) Делаем проверку.
Рассмотрим вычислительную машину и принцип ее работы.
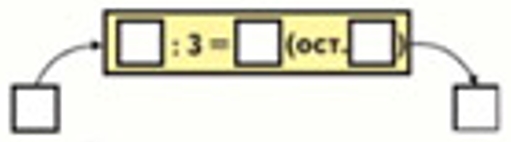
Выполним вычисления, пользуясь вычислительной машиной.
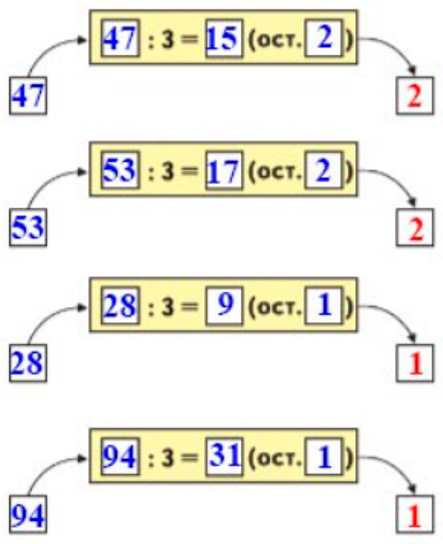
Оформим задание в тетрадь.
При выходе из машины получится:
1) При вводе числа 47 – остаток 2.
2) При вводе числа 53 – остаток 2.
3) При вводе числа 28 – остаток 1.
4) При вводе числа 94 – остаток 1.
Задание на полях страницы
Сравни площади фигур.


Площади фигур равны.
Для того, чтобы сравнить площади фигур, надо посчитать количество клеточек, которое они занимают.
Рассмотрим фигуры на полях страницы.
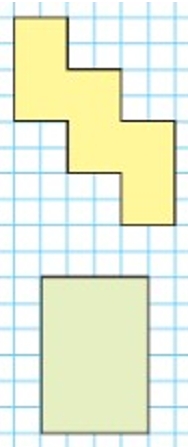
Найдем площади данных фигур и сравним их.
Посчитаем, сколько клеток занимает каждая фигура, и сравним результат.
• жёлтая фигура – 24 клетки;
• зелёная фигура – 24 клетки.
24 = 24.
Значит, площади этих фигур равны.
Записываем ответ.
Ответ: площади фигур равны.
Номер 130.
1) Из посёлка вышли одновременно в противоположных направлениях два пешехода. Скорость одного пешехода 5 км/ч, скорость другого 4 км/ч. На каком расстоянии друг от друга будут пешеходы через 3 ч?
2) Из посёлка вышли одновременно в противоположных направлениях два пешехода. Скорость одного пешехода 5 км/ч, скорость другого 4 км/ч. Через сколько часов расстояние между ними будет 27 км?
3) Из посёлка вышли одновременно в противоположных направлениях два пешехода. Через 3 ч расстояние между ними было 27 км. Первый пешеход шёл со скоростью 5 км/ч. С какой скоростью шёл второй пешеход?



Задача 1:
1) 5 + 4 = 9 (км/ч) – скорость удаления пешеходов.
2) 9 ∙ 3 = 27 (км) – расстояние между пешеходами.
Ответ: расстояние между пешеходами составляет 27 км.
Задача 2:
1) 5 + 4 = 9 (км/ч) – скорость удаления пеш.
2) 27 : 9 = 3 (ч) – через столько расстояние будет 27 км.
Ответ: через 3 часа расстояние между пешеходами составит 27 км.
Задача 3:
1) 5 ∙ 3 = 15 (км) – прошёл 1-ый пешеход.
2) 27 − 15 = 12 (км) – прошел 2-ой пешеход.
3) 12 : 3 = 4 (км/ч) – скорость второго пешехода.
Ответ: скорость второго пешехода составляет 4 км/ч.
1) Чтобы найти расстояние, надо скорость умножить на время.
2) Чтобы найти скорость, надо расстояние разделить на время.
3) Чтобы найти время, надо расстояние разделить на скорость.
Шаг 1.
Оформляем условие в виде схематического чертежа (из учебника).
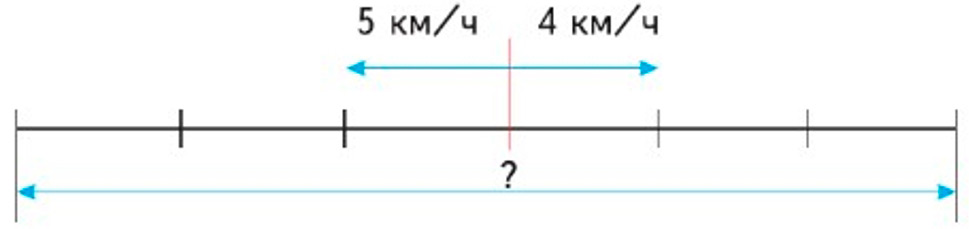
Рассуждаем.
Узнаем общую скорость пешеходов, с которой они удаляются друг от друга.
5 + 4 = 9 (км/ч) – скорость удаления пешеходов.
Продолжаем рассуждение.
Чтобы узнать расстояние между пешеходами, нужно общую скорость пешеходов умножить на время в пути.
9 ∙ 3 = 27 (км) – расстояние между пешеходами.
Записываем ответ.
Ответ: на расстоянии 27 км будут пешеходы друг от друга.
Шаг 1.
Оформляем условие в виде схематического чертежа (из учебника).
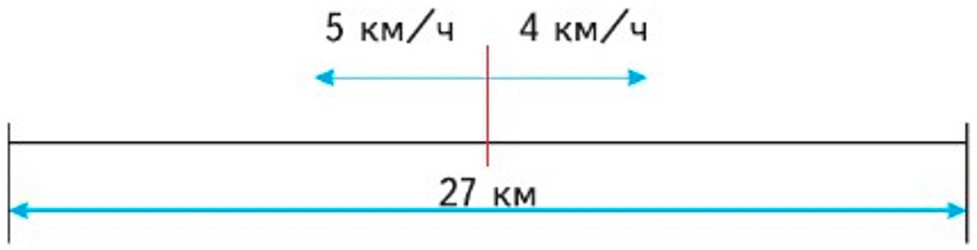
Рассуждаем.
Узнаем общую скорость пешеходов, с которой они удаляются друг от друга.
5 + 4 = 9 (км/ч) – скорость удаления пешеходов.
Продолжаем рассуждение.
Чтобы узнать, через какое время расстояние между пешеходами будет 27 км, нужно расстояние разделить на общую скорость пешеходов.
27 : 9 = 3 (ч) – через столько расстояние будет 27 км.
Записываем ответ.
Ответ: через 3 часа.
Шаг 1.
Оформляем условие в виде схематического чертежа (из учебника).
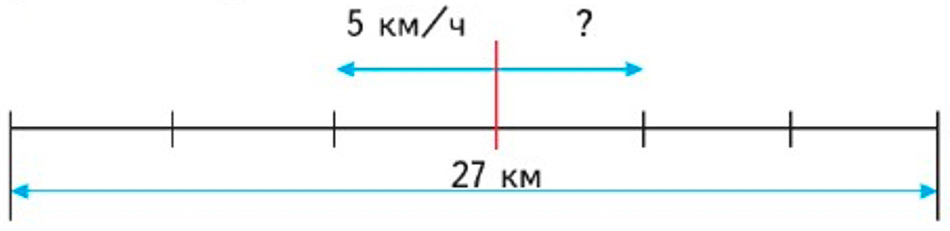
Рассуждаем.
Чтобы узнать, какое расстояние прошел первый пешеход, нужно скорость, с которой он двигался, умножить на время в пути.
5 ∙ 3 = 15 (км) – прошёл 1-ый пешеход.
Продолжаем рассуждение.
Чтобы узнать, какое расстояние прошел второй пешеход, нужно из общего расстояния вычесть расстояние, которое прошел первый пешеход.
27 − 15 = 12 (км) – прошел 2-ой пешеход.
Продолжаем рассуждение.
Чтобы узнать скорость второго пешехода, нужно расстояние, которое он прошел разделить на время в пути.
12 : 3 = 4 (км/ч) – скорость второго пешехода.
Записываем ответ.
Ответ: со скоростью 4 км/ч шёл второй пешеход.
Номер 131.
Составь и реши 3 похожие задачи.
Ответ:Задача 1: От автовокзала отошли одновременно в противоположных направлениях два автобуса. Средняя скорость одного автобуса 70 км/ч, другого – 60 км/ч. На каком расстоянии друг от друга будут автобусы через 2 часа?

1) 70 + 60 = 130 (км/ч) – скорость удаления авт.
2) 130 ∙ 2 = 260 (км) – будут автобусы друг от друга через 2 часа
Ответ: 260 км расстояние между автобусами.
Задача 2:
От автовокзала отошли одновременно в противоположных направлениях два автобуса. Скорость одного автобуса 70 км/ч, другого – 60 км/ч. Через сколько часов расстояние между ними будет 260 км?

1) 70 + 60 = 130 (км/ч) – скорость удаления автобусов.
2) 260 : 130 = 2 (ч) – расстояние будет 260 км
Ответ: через 2 часа расстояние между автобусами будет в 260 км.
Задача 3:
От автовокзала отъехали одновременно в противоположных направлениях два автобуса. Через 2 часа расстояние между ними было 260 км. Первый автобус ехал со скоростью 70 км/ч. С какой скоростью ехал второй автобус?

1) 70 ∙ 2 = 140 (км) – проехал 1-ый автобус.
2) 260 − 140 = 120 (км) – проехал 2-ой автобус.
3) 120 : 2 = 60 (км/ч) – скорость второго автобуса
Ответ: 60 км/ч скорость 2-ого автобуса.
1) Чтобы найти расстояние, надо скорость умножить на время.
2) Чтобы найти скорость, надо расстояние разделить на время.
3) Чтобы найти время, надо расстояние разделить на скорость.
Шаг 1.
Составляем условие первой задачи.
От автовокзала отошли одновременно в противоположных направлениях два автобуса. Средняя скорость одного автобуса 70 км/ч, другого – 60 км/ч. На каком расстоянии друг от друга будут автобусы через 2 часа?
Оформляем условие в виде схематического чертежа.

Рассуждаем.
Найдем скорость удаления автобусов, для этого сложим скорости автобусов вместе.
70 + 60 = 130 (км/ч) – скорость удаления автобусов.
Продолжаем рассуждение.
Найдем, на каком расстоянии будут друг от друга автобусы через 2 часа. Для этого общую скорость автобусов умножим на время в пути.
130 ∙ 2 = 260 (км) – расстояние между автобусами через 2 часа.
Записываем ответ.
Ответ: 260 км расстояние между автобусами.
Шаг 1.
Составляем условие второй задачи.
От автовокзала отошли одновременно в противоположных направлениях два автобуса. Скорость одного автобуса 70 км/ч, другого – 60 км/ч. Через сколько часов расстояние между ними будет 260 км?
Оформляем условие в виде схематического чертежа.
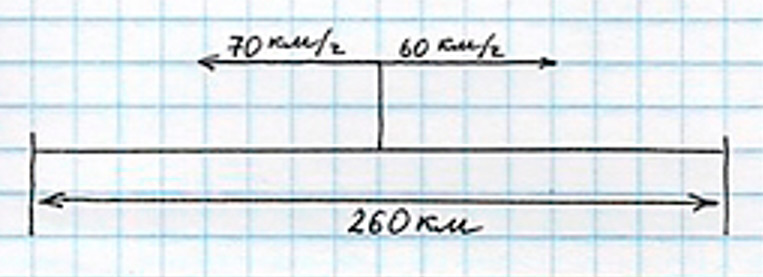
Рассуждаем.
Найдем скорость удаления автобусов, для этого сложим скорости автобусов вместе.
70 + 60 = 130 (км/ч) – скорость удаления автобусов.
Продолжаем рассуждение.
Чтобы найти время, которое автобусы были в пути, нужно расстояние разделить на скорость удаления автобусов.
260 : 130 = 2 (ч) – автобусы были в пути.
Записываем ответ.
Ответ: через 2 часа.
Шаг 1.
Составляем условие третьей задачи.
От автовокзала отъехали одновременно в противоположных направлениях два автобуса. Через 2 часа расстояние между ними было 260 км. Первый автобус ехал со скоростью 70 км/ч. С какой скоростью, ехал второй автобус?
Оформляем условие в виде схематического чертежа.
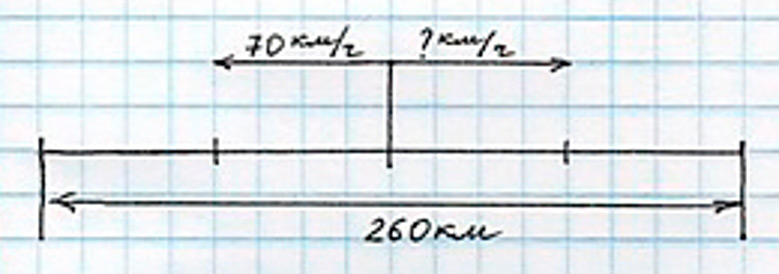
Рассуждаем.
Чтобы узнать, какое расстояние проехал первый автобус, нужно скорость его движения умножить на время в пути.
70 ∙ 2 = 140 (км) – проехал 1-ый автобус.
Продолжаем рассуждение.
Чтобы узнать, какое расстояние проехал второй автобус, нужно из общего расстояния вычесть расстояние, которое проехал первый автобус.
260 − 140 = 120 (км) – проехал 2-ой автобус.
Продолжаем рассуждение.
Чтобы узнать, с какой скоростью двигался второй автобус, нужно расстояние, которое он преодолел разделить на время в пути.
120 : 2 = 60 (км/ч) – скорость 2-ого автобуса.
Записываем ответ.
Ответ: 60 км/ч скорость второго автобуса.
Номер 132.
В киоске продавали тетради: школьные по цене а р. за тетрадь, общие по цене с р. за тетрадь. Сколько стоят вместе 5 школьных тетрадей и 5 общих? Запиши выражения, которые показывают, как можно решить эту задачу двумя способами.
1) (а + с) ∙ 5 2) а ∙ 5 + с ∙ 5
Вспомни свойства умножения.
Оформляем условие задачи в виде таблицы.

Шаг 1.
Рассуждаем.
Для начала узнаем стоимость школьных тетрадей, для этого умножим цену одной такой тетради на количество школьных тетрадей.
а ∙ 5 (руб.) – стоимость школьных тетрадей.
Продолжаем рассуждение.
Теперь узнаем стоимость общих тетрадей, для этого умножим цену одной такой тетради на количество общих тетрадей.
с ∙ 5 (руб.) – стоимость общих тетрадей.
Продолжаем рассуждение.
Чтобы узнать стоимость всех тетрадей, нужно сложить стоимость школьных и стоимость общих тетрадей.
а ∙ 5 + с ∙ 5 (руб.) – стоят школьные и общие тетради вместе.
Записываем ответ.
Ответ: а ∙ 5 + с ∙ 5 рублей стоят школьные и общие тетради вместе.
Шаг 1.
Рассуждаем.
Так как количество школьных и общих тетрадей одинакова, узнаем общую цену одной школьной и одной общей тетради, для этого сложим их цены.
а + с (руб.) – общая цена одной школьной и одной общей тетради.
Продолжаем рассуждение.
Чтобы узнать стоимость всех тетрадей, нужно общую цену одной школьной и одной общей тетради умножить на количество тетрадей.
(а + с) ∙ 5 (руб.) – стоят школьные и общие тетради вместе.
Записываем ответ.
Ответ: (а + с) ∙ 5 рублей стоят школьные и общие тетради вместе.
Номер 133.
Ответ:

1) Помним о порядке выполнения арифметических действий, и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем, действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Вычисляем.
Расставим порядок действий и вычислим по действиям.
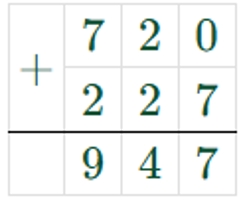
10000 − 2178 ∙ 6 ∶ 4 + 267 = 7000
1) 2178 ∙ 6 = 13068
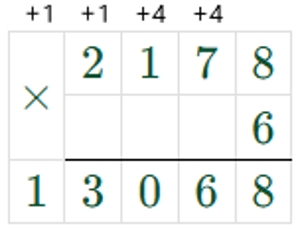
2) 13068 : 4 = 3267
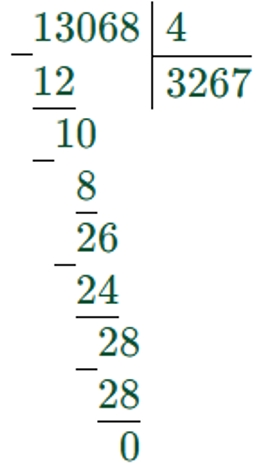
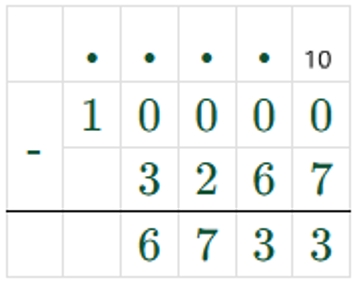
3) 10000 – 3267 = 6733
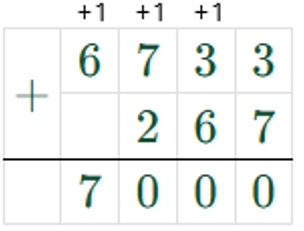
4) 6733 + 267 = 7000
Продолжаем рассуждения.
Расставим порядок действий и вычислим по действиям.
240 ∙ 3 + 4540 ∶ 20 = 947
1) 240 ∙ 3 = 720
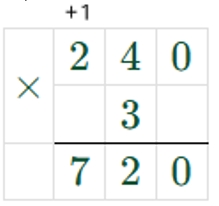
2) 4540 : 20 = 227
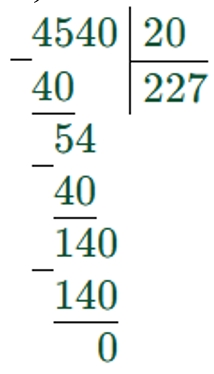
3) 720 + 227 = 947
Оформляем задание в тетрадь.
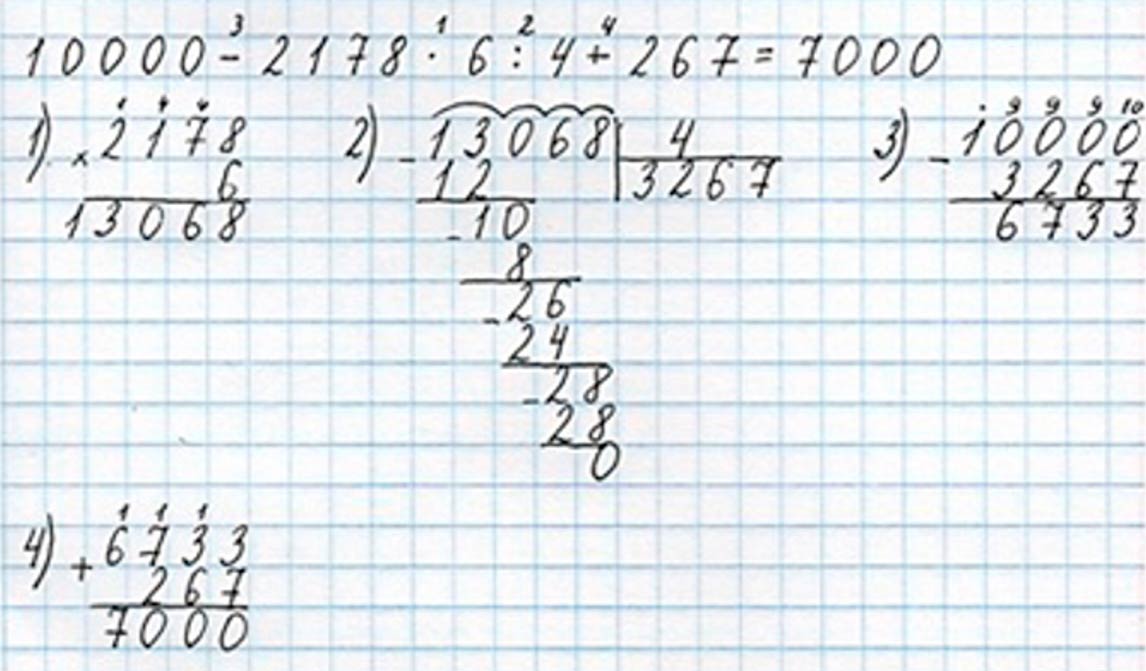
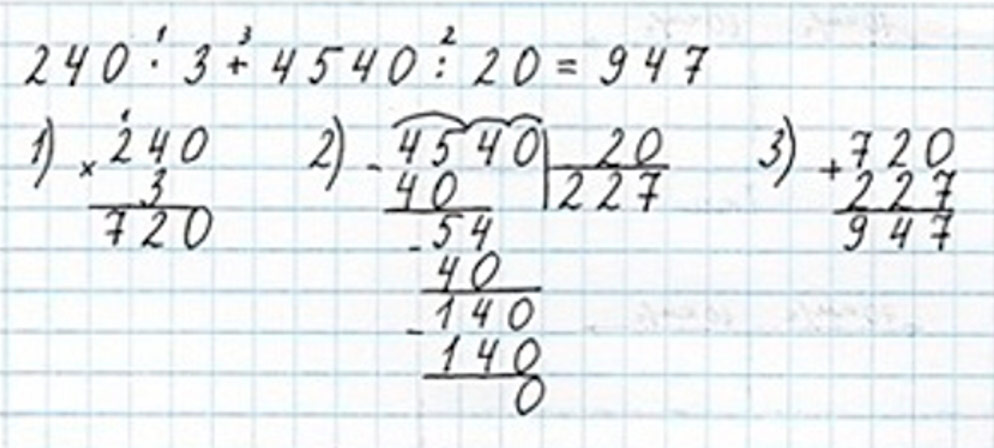
Задание внизу страницы
Ответ:

1) Помним о порядке выполнения арифметических действий, и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем, действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Вычисляем.
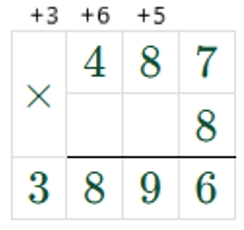
487 ∙ 8 + 45270 ∶ 3 ∶ 10 = 5405
1) 487 ∙ 8 = 3896
2) 45270 : 3 = 15090
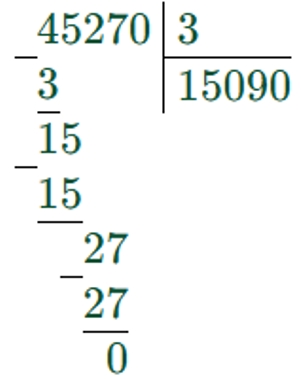
3) 15090 : 10 = 1509
Чтобы разделить число на 10, нужно справа у числа отбросить один нуль.
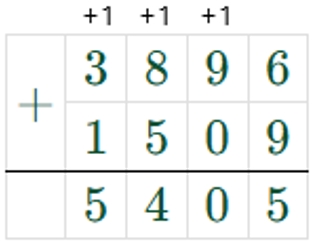
4) 3896 + 1509 = 5405
Продолжаем рассуждения.
Расставим порядок действий и вычислим по действиям.
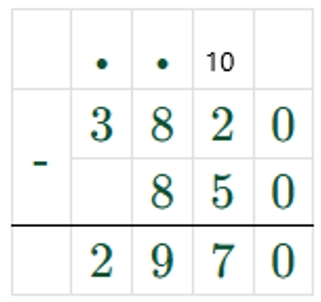
560 ∶ 7 + (3820 – 850) = 3050
1) 3820 – 850 = 2970
2) 560 : 7 = 56 дес. : 7 = 8 дес. = 80
3) 80 + 2970 = 3050
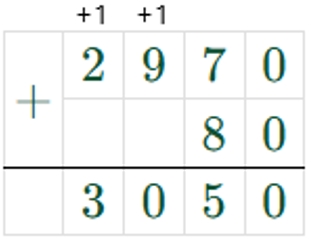
Оформляем задание в тетрадь.
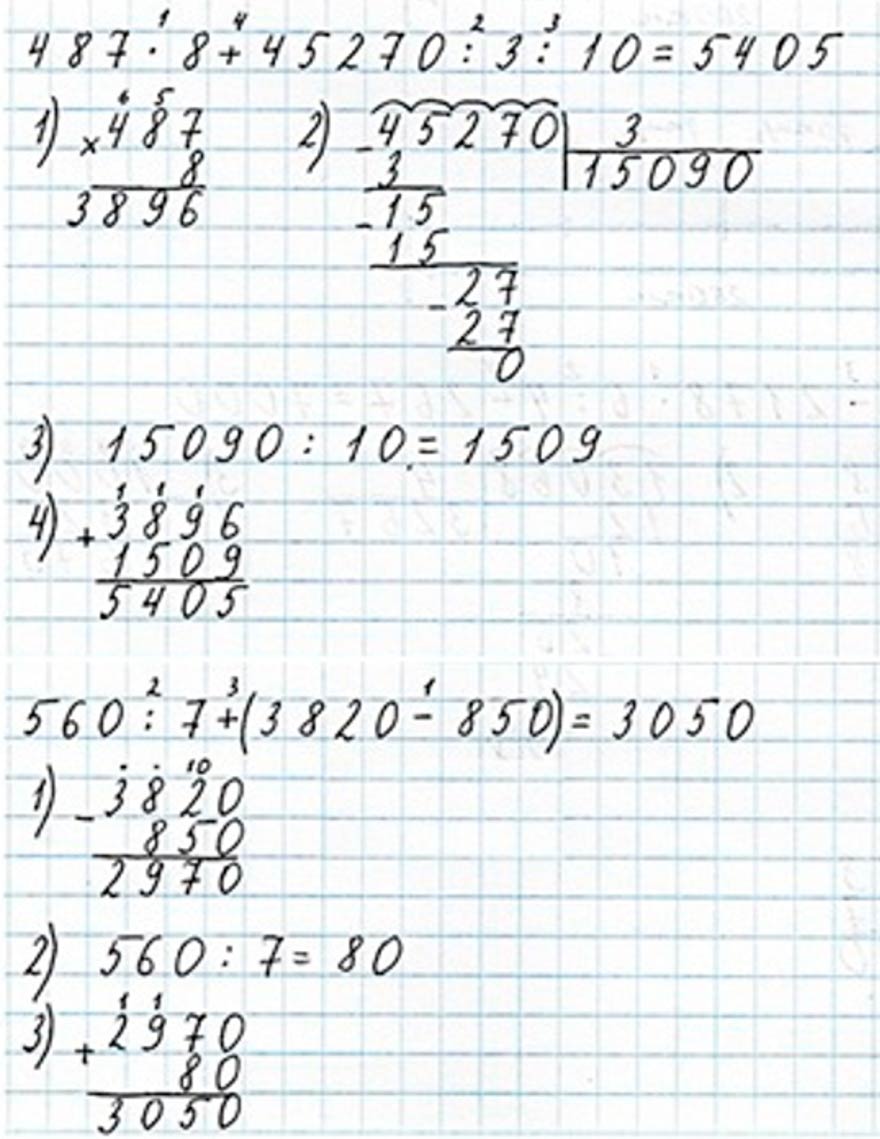
Задание на полях страницы
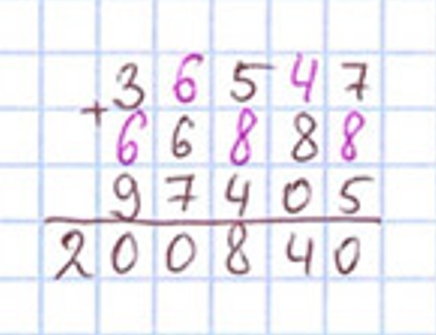
Ребус.


Вспомни, как складывать многозначные числа столбиком.
Рассмотрим ребус.

Сложили 3 слагаемых и получили сумму. Некоторые цифры этих слагаемых неизвестны.
Рассуждаем.
Многозначные числа складываются по разрядам справа налево, начиная с разряда единиц.
Рассмотрим разряд единиц.
Во втором слагаемом неизвестна цифра из разряда единиц.
Обозначим её за х, получим уранение:
7 + х + 5 = *0
х + 12 = *0
Сумма может быть только двузначным числом, заканчивающимся на 0, а х – только однозначным, значит
8 + 12 = 20
В сумме в единицах – 0, а 2 дес. запоминаем и прибавляем к десяткам.
х = 8 – цифра в разряде единиц второго слагаемого.
Рассмотрим разряд десятков.
В первом слагаемом неизвестна цифра из разряда десятков.
Обозначим её за х, получим уранение:
х + 8 + 0 + 2 (запомнили) = *4
х + 10 = *4
Сумма может быть только двузначным числом, заканчивающимся на 4, а х – только однозначным, значит
4 + 10 = 14
В сумме в десятках – 4, а 1 сот. запоминаем и прибавляем к сотням.
х = 4 – цифра в разряде десятков первого слагаемого.
Рассмотрим разряд сотен.
Во втором слагаемом неизвестна цифра из разряда сотен.
Обозначим её за х, получим уранение:
5 + х + 4 + 1 (запомнили) = *8
х + 10 = *8
Сумма может быть только двузначным числом, заканчивающимся на 8, а х – только однозначным, значит
8 + 10 = 18
В сумме в сотнях – 8, а 1 тыс. запоминаем и прибавляем к тысячам.
х = 8 – цифра в разряде сотен второго слагаемого.
Рассмотрим разряд тысяч.
В первом слагаемом неизвестна цифра из разряда тысяч.
Обозначим её за х, получим уранение:
х + 6 + 7 + 1 (запомнили) = *0
х + 14 = *0
Сумма может быть только двузначным числом, заканчивающимся на 0, а х – только однозначным, значит
6 + 14 = 20
В сумме в тысячах – 0, а 2 дес.тыс. запоминаем и прибавляем к десяткам тысяч.
х = 6 – цифра в разряде тысяч первого слагаемого.
Рассмотрим разряд десяток тысяч.
Во втором слагаемом неизвестна цифра из разряда десяток тысяч.
Обозначим её за х, получим уранение:
3 + х + 9 + 2 (запомнили) = 20
х + 14 = 20
х = 20 – 14
х = 6 – цифра в разряде десяток тысяч второго слагаемого.
Оформим задание в тетрадь.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.