Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 28

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 95.
Из 2 м полотна получается 3 наволочки. Сколько таких наволочек получится из 42 м полотна?

2 м – 3 н.
42 м – ? н.
1) 42 : 2 = 21 (раз) – вмещается по 2 м в 42 м.
2) 3 ∙ 21 = 63 (н.) - получится из 42 м полотна
Ответ: 63 наволочки всего получится из 42 м полотна.
Оформляем условие задачи в виде таблицы.
Оформляем условие.

Рассуждаем.
Узнаем, сколько раз по 2 метра вмещается в 42 метрах.
1) 42 : 2 = 21 (раз) – вмещается по 2 м в 42 м.
Продолжаем рассуждение.
Чтобы узнать, сколько наволочек получится из 42 метров полотна, надо 21 умножить на 3.
2) 21 ∙ 3 = 63 (н.)
Записываем ответ.
Ответ: 63 наволочки.
Номер 96.
В 10 одинаковых банках 16 кг мёда. Сколько килограммов мёда в 20 таких банках?
Ответ:
10 б. – 16 кг
20 б. – ? кг
1) 20 : 10 = 2 (раза) – во столько раз банок взяли больше.
2) 16 ∙ 2 = 32 (кг) - мёда всего в 20 банках
Ответ: 32 кг мёда в 20 банках.
Оформляем условие задачи в виде таблицы.
Оформляем условие.

Рассуждаем.
Узнаем, во сколько раз банок взяли больше.
1) 20 : 10 = 2 (раза) – во столько раз банок взяли больше.
Продолжаем рассуждение.
Узнаем, сколько кг меда в 20 банках, для этого 16 умножим на 2.
2) 16 ∙ 2 = 32 (кг)
Записываем ответ.
Ответ: 32 кг мёда в 20 банках.
Номер 97.
Из двух городов выехали одновременно навстречу друг другу два мотоциклиста. Один из них двигался со скоростью 70 км/ч и проехал до встречи 140 км, а другой двигался со скоростью 65 км/ч. Найди расстояние между городами. Составь и реши задачи, обратные данной.
Ответ:
1) 140 : 70 = 2 (ч) – в пути.
2) 65 ∙ 2 = 130 (км) – проехал второй мотоциклист.
3)140 + 130 = 270 (км) – расстояние между городами.
Ответ: 270 км всего расстояние между городами.
Обратная задача 1:
Из двух городов, расстояние между которыми 270 км, выехали одновременно навстречу друг другу два мотоцикла. Один из них двигался со скоростью 70 км/ч, и проехал 140 км. С какой скоростью двигался второй мотоциклист?
1) 140 : 70 = 2 (ч) – время движения.
2) 270 − 140 = 130 (км) – проехал 2-ой мотоциклист.
3) 130 : 2 = 65 (км/ч) – скорость 2-ого мотоциклиста.
Ответ: скорость второго мотоциклиста составляет 65 км/ч.
Обратная задача 2:
Из двух городов, расстояние между которыми 270 км, выехали одновременно навстречу друг другу два мотоцикла. Один из них двигался со скоростью 65 км/ч, и проехал 130 км. С какой скоростью двигался первый мотоциклист?
1) 130 : 65 = 2 (ч) – время движения.
2) 270 − 130 = 140 (км) – проехал 1-ый мотоциклист.
3) 140 : 2 = 70 (км/ч) – скорость 1-ого мотоциклиста.
Ответ: скорость первого мотоциклиста составляет 70 км/ч.
S = V ∙ t: Чтобы найти расстояние, надо скорость умножить на время.
V = S : t: Чтобы найти скорость, надо расстояние разделить на время.
t = S : V: Чтобы найти время, надо расстояние разделить на скорость.
Шаг 1.
Оформляем условие в виде схематического чертежа.
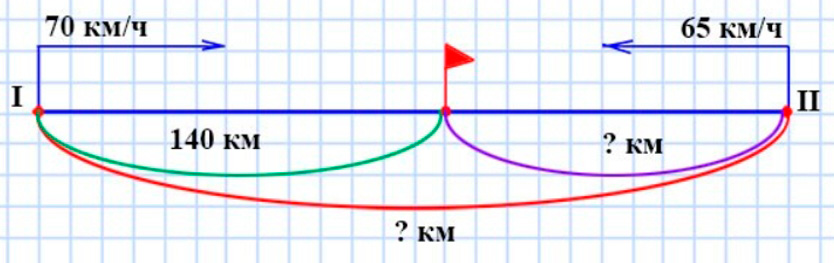
Рассуждаем.
Узнаем, какое время мотоциклисты были в пути. Для этого расстояние, которое проехал первый мотоциклист разделим на его скорость.
1) 140 : 70 = 2 (ч) – в пути.
Продолжаем рассуждение.
Зная время, мы можем узнать расстояние, которое проехал второй мотоциклист. Для этого скорость второго мотоциклиста умножаем на время.
2) 65 ∙ 2 = 130 (км) – проехал второй мотоциклист.
Продолжаем рассуждение.
Чтобы узнать расстояние между городами, нужно сложить вместе расстояния, которые проехали оба мотоциклиста до встречи друг с другом.
3) 140 + 130 = 270 (км) – расстояние между городами.
Записываем ответ.
Ответ: 270 км.
Шаг 1.
Составляем задачу обратную данной.
Из двух городов, расстояние между которыми 270 км, выехали одновременно навстречу друг другу два мотоциклиста. Один из них двигался со скоростью 70 км/ч, а другой 65 км/ч. Через какое время они встретились?
Оформляем условие в виде схематического чертежа.
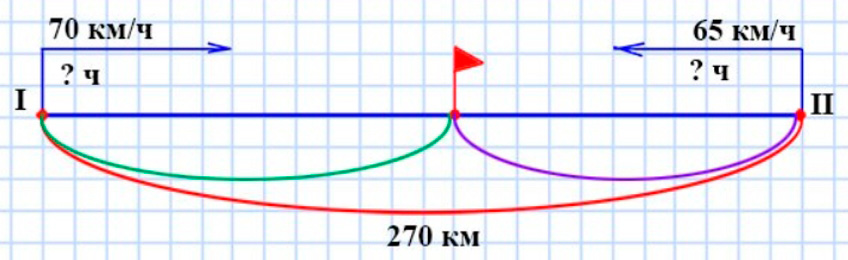
Рассуждаем.
Найдем скорость сближения мотоциклистов, для этого сложим вместе скорость каждого.
1) 70 + 65 = 135 (км/ч) – совместная скорость (скорость сближения) мотоциклистов.
Продолжаем рассуждение.
Чтобы найти время, которое оба мотоциклиста были в пути, нужно расстояние разделить на скорость сближения.
2) 270 : 135 = 2 (ч) – двигались мотоциклисты до встречи.
Записываем ответ.
Ответ: через 2 ч.
Шаг 1.
Составляем задачу обратную данной.
Из двух городов, расстояние между которыми 270 км, выехали одновременно навстречу друг другу два мотоциклиста. Второй мотоциклист ехал со скоростью 65 км/ч. С какой скоростью, двигался первый мотоциклист, если они встретились через 2 часа?
Оформляем условие в виде схематического чертежа.
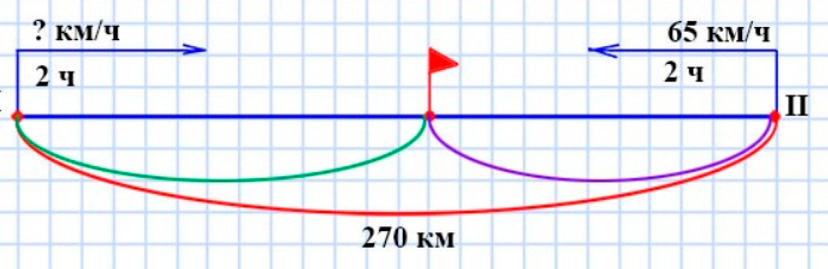
Рассуждаем.
Найдем скорость сближения мотоциклистов, для этого сложим вместе скорость каждого.
1) 70 + 65 = 135 (км/ч) – совместная скорость (скорость сближения)
Продолжаем рассуждение.
Чтобы найти скорость движения первого мотоциклиста, нужно из скорости сближения вычесть скорость второго мотоциклиста.
2) 137 – 65 = 70 (км/ч) – скорость движения первого мотоциклиста.
Записываем ответ.
Ответ: 70 км/ч.
Номер 98.
Запиши равенства и неравенства, проверь, верны ли они.
1) Произведение чисел 293 и 70 равно разности чисел 2900 и 849.
2) Сумма чисел 9391 и 7028 равна частному чисел 82095 и 5.
3) Частное чисел 70236 и 9 меньше их разности.
4) Произведение чисел 8019 и 7 больше их суммы.
1) 293 ∙ 70 = 2900 − 849 – неверно 2) 9391 + 7028 = 82095 : 5 – верно 3) 70236 : 9 < 70236 − 9 – верно 4) 8019 ∙ 7 > 8019 + 7 – верно


«>» – знак «больше»
«<» – знак «меньше»
«=» – знак «равно»
Запишем равенства и неравенства и проверим верны ли они.
1) 293 ∙ 70 = 2900 − 849 – неверно
2) 9391 + 7028 = 82095 : 5 – верно
3) 70236 : 9 < 70236 − 9 – верно
4) 8019 ∙ 7 > 8019 + 7 – верно
Оформим задание в тетрадь.

Номер 99.
Выполни деление с остатком и проверь решение.
Ответ:1724 : 10 = 172 (ост.4) Проверка: 1) 4 < 10 2) 172 ∙ 10 + 4 = 1724 1720 2540 : 100 = 25 (ост.40) Проверка: 1) 40 < 100 2) 25 ∙ 100 + 40 = 2540 2500 65032 : 1000 = 65 (ост.32) Проверка: 1) 32 < 1000 2) 65 ∙ 1000 + 32 = 65032 65000
Алгоритм деления примеров с остатком.
1) Находим наибольшее число до делимого, которое можно разделить на делитель без остатка.
2) Данное число делим на делитель. Это значение частного.
3) Вычитаем из делимого наибольшее число – это остаток.
4) Проверяем, остаток должен быть меньше делителя.
5) Делаем проверку.
Выполним деление и проверим решение.
1724 : 10 = 172 (ост.4)
Проверка: 1) 4 < 10
2) 172 ∙ 10 + 4 = 1724
2540 : 100 = 25 (ост.40)
Проверка: 1) 40 < 100
2) 25 ∙ 100 + 40 = 2540
65032 : 1000 = 65 (ост.32)
Проверка: 1) 32 < 1000
2) 65 ∙ 1000 + 32 = 65032
Оформим задание в тетрадь.
1 724 : 10 = 172 (ост. 4)
2 540 : 100 = 23 (ост. 40)
65 032 : 1 000 = 65 (ост. 32)
Номер 100.
Ответ:


Алгоритм деления на 10, 100, 1000:
1. Представить делимое в виде суммы разрядных слагаемых.
2. Разделить первое слагаемое суммы на делитель.
3. Получить частное, назвать остаток.
4. Выполнить проверку: умножить частное на делитель, прибавить.
Выполняем вычисления с пояснениями.
140 : 20 = 14 дес. : 2 дес. = 7
560 : 7 = 56 дес. : 7 = 8 дес. = 80
8 100 : 900 = 81 сот. : 9 сот. = 9
3 200 : 800 =32 сот. : 8 сот. = 4
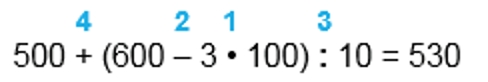
1) 3 ∙ 100 = 300
2) 600 – 300 = 300
3) 300 : 10 = 30
4) 500 + 30 = 530
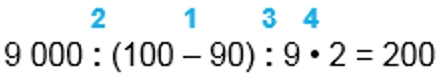
1) 100 – 90 = 10
2) 9000 : 10 = 900
3) 900 : 9 = 100
4) 100 ∙ 2 = 200
Оформим задание в тетрадь.

Номер 101.
У моей мамы рост 164 см. Мой брат на 16 см выше мамы, а я пока на 8 см ниже мамы. Какой у меня рост? Сделай схематический чертёж к задаче и определи, на сколько сантиметров брат выше меня.
Ответ:
1) 164 + 16 = 180 (см) – рост брата.
2) 164 − 8 = 156 (см) – мой рост.
3) 180 − 156 = 24 (см) – разница.
Задачу проще решить, сделав схематический чертёж:

8 + 16 = 24 (см) - всего брат выше меня
Ответ: на 24 см брат выше меня.
Чтобы узнать, насколько одно число больше или меньше другого, нужно из большего числа вычесть меньшее.
Оформляем условие в виде схематического чертежа.
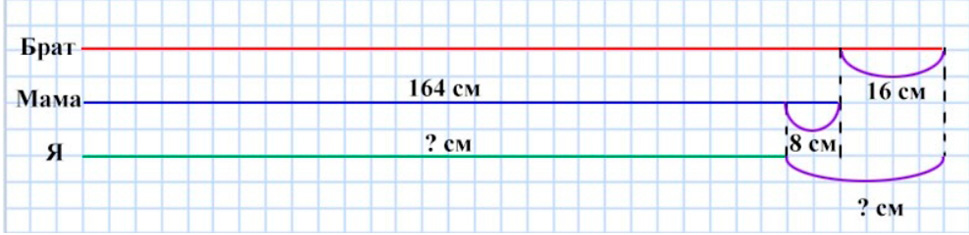
Рассуждаем.
Узнаем, какой рост у меня. Для этого из роста мамы вычтем 8 см, потому что известно, что я ниже мамы на 8 см.
1) 164 – 8 = 156 (см) – мой рост.
Продолжаем рассуждение.
Теперь узнаем, на сколько сантиметров мой брат выше меня, для этого нужно сложить 16 см, на которые он выше мамы и 8 смс на которые мама выше меня.
2) 16 + 8 = 24 (см) – настолько см мой брат выше меня.
Записываем ответ.
Ответ: мой рост – 156 см, брат выше на 24 см.
Задание внизу страницы
Сумма трёх чисел 2010. Первое слагаемое 980, оно в 2 раза больше второго. Найди третье слагаемое.
Ответ:
1) 980 : 2 = 490 – слагаемое.
2) 980 + 490 = 1470 – сумма 1 и 2 слагаемых.
3) 2010 – 1470 = 540 – третье слагаемое.
Выражение:
2010 − (980 + 980 : 2) = 540
Ответ: 540 третье слагаемое.
Оформляем условие задачи в виде краткой записи.
Оформляем условие.
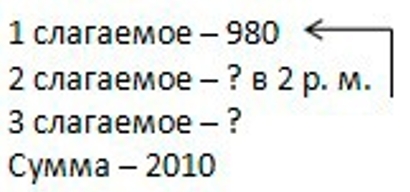
Рассуждаем.
Найдем второе слагаемое, для этого значение первого слагаемого разделим на 2, так как известно, что второе слагаемое в два раза меньше, чем первое.
1) 980 : 2 = 490 – 2 слагаемое.
Продолжаем рассуждение.
Узнаем сумму 1-го и 2-го слагаемых, для этого сложим их значения.
2) 980 + 490 = 1470 – сумма 1 и 2 слагаемых.
Продолжаем рассуждение.
Чтобы узнать значение третьего слагаемого, нужно из суммы всех значений вычесть сумму 1 и 2 слагаемых.
3) 2010 – 1470 = 540 – третье слагаемое.
Записываем ответ.
Ответ: 540 третье слагаемое.
Решение выражением: 2010 − (980 + 980 : 2) = 540
Задание на полях страницы

Ответ:

Внимательно рассмотри данные примеры, найди значение каждой фигуры и реши их.
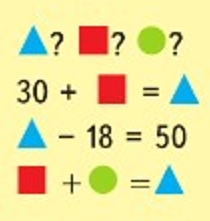
Найдем значение каждой фигуры.
1) 50 + 48 = 68 – синий треугольник (из второго равенства)
2) 68 – 30 = 38 – красный квадрат (из первого равенства)
3) 38 – 38 = 30 – зелёный круг (из третьего равенства)
Ответ: Синий треугольник – число 68, красный квадрат – число 38, зелёный круг – число 30.
Выполним вычисления и оформим задание в тетрадь.

Номер 83.
Вычисли удобным способом.
Ответ:240 : (4 ∙ 10) = (240 : 10) : 4 = 24 : 4 = 6 180 : (2 ∙ 10) = (180 : 10) : 2 = 18 : 2 = 9 540 : (9 ∙ 10) = (540 : 10) : 9 = 54 : 9 = 6
1) Помни, как разделить число на произведение.
2) Чтобы разделить число на 10, нужно справа у этого числа отбросить один нуль.
Вычисляем.
240 : (4 ∙ 10) = (240 : 10) : 4 = 24 : 4 = 6
Удобнее сначала разделить число 240 на второй множитель – 10, а полученный результат уже разделить на второй множитель – 4.
180 : (2 ∙ 10) = (180 : 10) : 2 = 18 : 2 = 9
Удобнее сначала разделить число 180 на второй множитель – 10, а полученный результат уже разделить на второй множитель – 2.
540 : (9 ∙ 10) = (540 : 10) : 9 = 54 : 9 = 6
Удобнее сначала разделить число 540 на второй множитель – 10, а полученный результат уже разделить на второй множитель – 9.
Оформляем задание в тетрадь.
240 : (4 ∙ 10) = (240 : 10) : 4 = 24 : 4 = 6
180 : (2 ∙ 10) = (180 : 10) : 2 = 18 : 2 = 9
540 : (9 ∙ 10) = (540 : 10) : 9 = 54 : 9 = 6
Номер 84.
Объясни, как выполнено деление.
Ответ:
360 : 12 = 360 : (6 ∙ 2) = 360 : 6 : 2 = 30 – делитель представлен в виде произведения, а затем разделить число на первый множитель и результат разделить на второй множитель.
7200 : 900 = 7200 : (100 ∙ 9) = 7200 : 100 : 9 = 8 – делитель представлен в виде произведения, а затем разделить число на первый множитель и результат разделить на второй множитель.
1) Помни, как разделить число на произведение.
2) Чтобы разделить число на 100, нужно справа у этого числа отбросить два нуля.
Рассуждаем.
360 : 12 = 360 : (6 ∙ 2) = (360 : 6) : 2 = 60 : 2 = 30
Делитель 12 представили в виде произведения чисел 6 и 2, затем разделили число 360 на первый множитель – 6, а полученный результат разделили уже на второй множитель – 2.
Продолжаем рассуждения.
7200 : 900 = 7200 : (100 ∙ 9) = (7200 : 100) : 9 = 72 : 9 = 8
Делитель 900 представили в виде произведения чисел 100 и 9, затем разделили число 7200 на первый множитель – 100, а полученный результат разделили уже на второй множитель – 9.
Номер 85.
Выполни деление, заменив делитель произведением.
Ответ:600 : 20 = 600 : (10 ∙ 2) = (600 : 10) : 2 = 30 300 : 15 = 300 : (3 ∙ 5) = (300 : 3) : 5 = 20 420 : 14 = 420 : (7 ∙ 2) = (420 : 7) : 2 = 30 5600 : 800 = 5600 : (100 ∙ 8) = (5600 : 100) : 8 = 7.
1) Помни, как разделить число на произведение.
2) Помни, как разделить число на 10 и на 100.
Вычисляем.
600 : 20 = 600 : (10 ∙ 2) = (600 : 10) : 2 = 60 : 2 = 30
Представим делитель 20 в виде произведения чисел 10 и 2, разделим число 600 на первый множитель – 10, затем полученный результат разделим на второй множитель – 2.
300 : 15 = 300 : (3 ∙ 5) = (300 : 3) : 5 = 100 : 5 = 20
Представим делитель 15 в виде произведения чисел 3 и 5, разделим число 300 на первый множитель – 3, затем полученный результат разделим на второй множитель – 5.
420 : 14 = 420 : (7 ∙ 2) = (420 : 7) : 2 = 60 : 2 = 30
Представим делитель 14 в виде произведения чисел 7 и 2, разделим число 420 на первый множитель – 7, затем полученный результат разделим на второй множитель – 2.
5600 : 800 = 5600 : (100 ∙ 8) = (5600 : 100) : 8 = 56 : 8 = 7
Представим делитель 800 в виде произведения чисел 100 и 8, разделим число 5600 на первый множитель – 100, затем полученный результат разделим на второй множитель – 8.
Оформляем задание в тетрадь.
600 : 20 = 600 : (10 ∙ 2) = 60 : 2 = 30
300 : 15 = 300 : (3 ∙ 5) = 100 : 5 = 20
420 : 14 = 420 : (7 ∙ 2) = 60 : 2 = 30
5600 : 800 = 5600 : (100 ∙ 8) = 56 : 8 = 7
Номер 86.
Ответ:
320 : 80 = 320 : (10 ∙ 8) = (320 : 10) : 8 = 4
810 : 90 = 810 : (10 ∙ 9) = (810 : 10) : 9 = 9
780 : 30 = 780 : (10 ∙ 3) = (780 : 10) : 3 = 26
560 : 20 = 560 : (10 ∙ 2) = (560 : 10) : 2 = 28
600 : 15 = 600 : (3 ∙ 5) = (600 : 3) : 5 = 40
280 : 70 = 280 : (10 ∙ 7) = (280 : 10) : 7 = 4
1200 : 200 = 1200 : (100 ∙ 2) = (1200 : 100) : 2 = 6
4900 : 700 = 4900 : (100 ∙ 7) = (4900 : 100) : 7 = 7
1) Помни, как разделить число на произведение.
2) Помни, как разделить число на 10 и на 100.
Вычисляем.
320 : 80 = 320 : (10 ∙ 8) = (320 : 10) : 8 = 32 : 8 = 4
Представим делитель 80 в виде произведения чисел 10 и 8, разделим число 320 на первый множитель – 10, затем полученный результат разделим на второй множитель – 8.
810 : 90 = 810 : (10 ∙ 9) = (810 : 10) : 9 = 81 : 9 = 9
Представим делитель 90 в виде произведения чисел 10 и 9, разделим число 810 на первый множитель – 10, затем полученный результат разделим на второй множитель – 9.
780 : 30 = 780 : (10 ∙ 3) = (780 : 10) : 3 = 78 : 3 = (60 + 18) : 3 = 20 + 6 = 26
Представим делитель 30 в виде произведения чисел 10 и 3, разделим число 780 на первый множитель – 10, затем полученный результат разделим на второй множитель – 3.
560 : 20 = 560 : (10 ∙ 2) = (560 : 10) : 2 = 56 : 2 = (40 + 16) : 2 = 20 + 8 = 28
Представим делитель 20 в виде произведения чисел 10 и 2, разделим число 560 на первый множитель – 10, затем полученный результат разделим на второй множитель – 2.
600 : 15 = 600 : (3 ∙ 5) = (600 : 3) : 5 = 200 : 5 = 40
Представим делитель 15 в виде произведения чисел 3 и 5, разделим число 600 на первый множитель – 3, затем полученный результат разделим на второй множитель – 5.
280 : 70 = 280 : (10 ∙ 7) = (280 : 10) : 7 = 28 : 7 = 4
Представим делитель 70 в виде произведения чисел 10 и 7, разделим число 280 на первый множитель – 10, затем полученный результат разделим на второй множитель – 7.
1200 : 200 = 1200 : (100 ∙ 2) = (1200 : 100) : 2 = 12 : 2 = 6
Представим делитель 200 в виде произведения чисел 100 и 2, разделим число 1200 на первый множитель – 100, затем полученный результат разделим на второй множитель – 2.
4900 : 700 = 4900 : (100 ∙ 7) = (4900 : 100) : 7 = 49 : 7 = 7
Представим делитель 700 в виде произведения чисел 100 и 7, разделим число 4900 на первый множитель – 100, затем полученный результат разделим на второй множитель – 7.
Оформляем задание в тетрадь.
320 : 80 = 320 : 10 : 8 = 32 : 8 = 4
810 : 90 = 810 : 10 : 9 = 81 : 9 = 9
780 : 30 = 780 : 10 : 3 = 78 : 3 = (60 + 18) : 3 = 20 + 6 = 26
560 : 20 = 560 : 10 : 2 = 56 : 2 = (40 + 16) : 2 = 20 + 8 = 28
600 : 15 = 600 : 3 : 5 = 200 : 5 = 40
280 : 70 = 280 : 10 : 7 = 28 : 7 = 4
1200 : 200 = 1200 : 100 : 2 = 12 : 2 = 6
4900 : 700 = 4900 : 100 : 7 = 49 : 7 = 7
Номер 87.
Из двух городов, расстояние между которыми 846 км, вышли одновременно навстречу друг другу два поезда. Один шёл со скоростью 85 км/ч, другой – со скоростью 60 км/ч. Какое расстояние будет между поездами через 3 ч?


Ответ: 411 км расстояние между поездами через 3 часа.
1) Чтобы найти расстояние, надо скорость умножить на время.
2) Чтобы найти скорость, надо расстояние разделить на время.
3) Чтобы найти время, надо расстояние разделить на скорость.
Рассмотрим рисунок.
Перенесём схематичный рисунок в тетрадь.
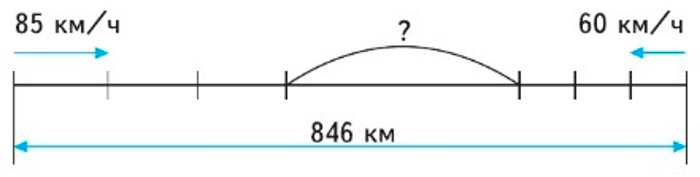
Время движения – 3 часа.
Рассуждаем.
Чтобы узнать общую скорость поездов, нужно сложить скорости одного и другого поезда.
85 + 60 = 145 (км/ч) – общая скорость поездов.
Продолжаем рассуждение.
Чтобы узнать, сколько км оба поезда проедут за 3 часа, нужно скорость сближения поездов умножить на время.
145 ∙ 3 = 435 (км) – проедут оба поезда за 3 часа.
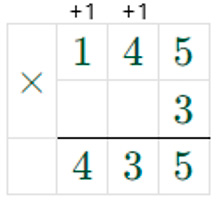
Продолжаем рассуждение.
Чтобы узнать, какое расстояние будет между поездами через 3 часа, нужно из расстояния между городами вычесть расстояние, которое они преодолели за 3 часа.
846 – 435 = 411 (км) – будет между поездами через 3 часа.
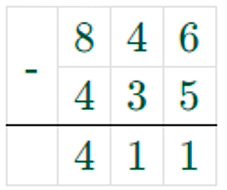
Записываем ответ.
Ответ: 411 км будет между поездами через 3 часа.
Номер 88.
В мастерской сшили 120 спальных мешков за 6 дней, изготавливая одинаковое количество мешков каждый день. За сколько дней сошьют 100 спальных мешков, если ежедневно будут шить на 5 мешков больше?
Ответ:
1) 120 : 6 = 20 (м.) – шили за 1 день.
2) 20 + 5 = 25 (м.) – будут шить за 1 день.
3) 100 : 25 = 4 (дн.) - всего сошьют 100 спальных мешков
Ответ: за 4 дня сошьют 100 спальных мешков.
Оформляем условие задачи в виде таблицы.
Оформляем условие.

Рассуждаем.
Узнаем, сколько мешков шили за один день. Для этого общее количество мешков разделим на количество дней.
120 : 6 = 20 (м.) – шили за один день.
Продолжаем рассуждение.
Узнаем, сколько мешков будут шить за один день, если их количество увеличится на 5.
20 + 5 = 25 (м.) – будут шить за один день.
Продолжаем рассуждение.
Узнаем, за сколько дней сошьют 100 мешков, разделив общее количество мешков на количество мешков в день.
100 : 25 = 4 (дн.) – нужно, чтобы сшить 100 мешков.
Записываем ответ.
Ответ: за 4 дня сошьют 100 спальных мешков.
Номер 89.
Коля задумал число, прибавил к нему 16, увеличил результат в 10 раз и получил 300. Какое число задумал Коля? Составь похожее задание.
Ответ:
Обозначим задуманное число за х, тогда
(х + 16) · 10 = 300
х + 16 = 300 : 10
х + 16 = 30
х = 30 – 16
х = 14
Задуманное число – 14.
Ответ: 14.
Задание: Из задуманного числа вычли 25, уменьшили результат в 5 раз и получили 10. Узнай задуманное число.
(х – 25) : 5 = 10
Ответ: Задуманное число – 75.
Уравнение – равенство с неизвестной, при подстановке числа в которую, получается верное равенство.
Рассуждаем.
Коля задумала какое-то число.
Обозначим это число за х, составим уравнение и решим его.
(х + 16) ∙ 10 = 300
х + 16 = 300 : 10
х + 16 = 30
х = 30 – 16
х = 14 – число, которое задумал Коля
Записываем ответ.
Ответ: Коля задумал число 14.
Составим задание.
Из задуманного числа вычли 25, результат уменьшили в 5 раз и получили 10. Узнай задуманное число.
Рассуждаем.
Обозначим задуманное число за х, составим уравнение и решим его.
(х – 25) : 5 = 10
х – 25 = 10 ∙ 5
х – 25 = 50
х = 50 + 25
х = 75 – задуманное число
Записываем ответ.
Ответ: 75 – задуманное число.
Номер 90.
Ответ:

1) Помним о порядке выполнения арифметических действий, и что скобки влияют на порядок выполнения действий.
2) Помни, как умножать и делить многозначные числа столбиком.
Вычисляем.
Выполним вычисления по действиям.
838008 : 9 – 410960 : 8 = 93112 – 51370 = 41742
Сначала выполняем действие деление по порядку слева направо, а затем – вычитание.
1) 838008 : 9 = 93112
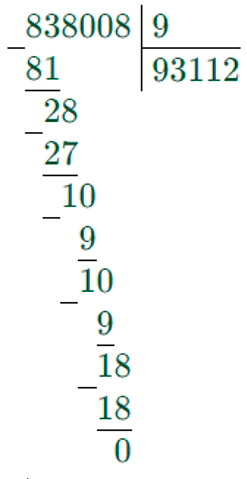
2) 410960 : 8 = 51370
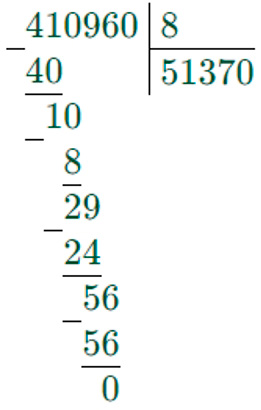
3) 93112 – 51370 = 41742
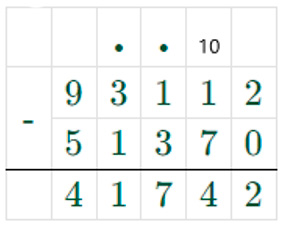
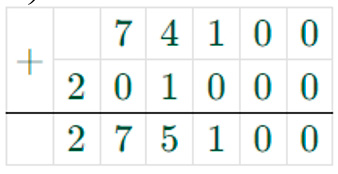
1482 ∙ 50 + 6700 ∙ 30 = 74100 + 201000 = 275100
Сначала выполняем действие умножение по порядку слева направо, а затем – сложение.
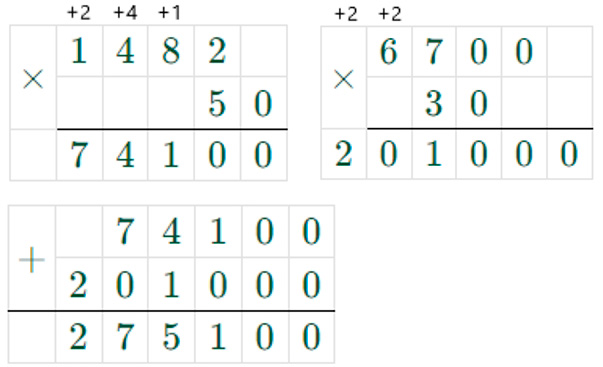
1) 1482 ∙ 50 = 74100
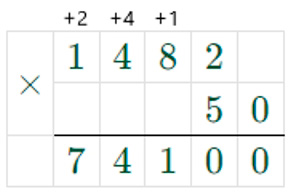
2) 6700 ∙ 30 = 201000
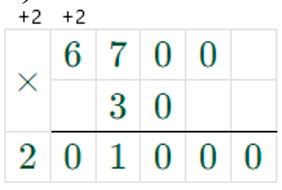
3) 74100 + 201000 = 275100
560000 : 100 ∙ 8 = 5600 ∙ 8 = 44800
Действия деление и умножение равнозначны, поэтому выполняем их по порядку слева направо, сначала – деление, потом – умножение.
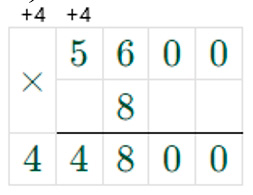
1) 560000 : 100 = 5600
Чтобы число разделить на 100, то нужно справа отбросить два нуля.
2) 5600 ∙ 8 = 44800
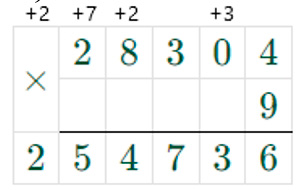
283040 : 10 ∙ 9 = 28304 ∙ 9 = 254736
Действия деление и умножение равнозначны, поэтому выполняем их по порядку слева направо, сначала – деление, потом – умножение.
1) 283040 : 10 = 28304
Чтобы число разделить на 10, то нужно справа отбросить один нуль.
2) 28304 ∙ 9 = 254736
Оформляем задание в тетрадь.
838008 : 9 – 410960 : 8 = 93112 – 51370 = 41742

1482 ∙ 50 + 6700 ∙ 30 = 74100 + 201000 = 275100
560000 : 100 ∙ 8 = 5600 ∙ 8 = 44800
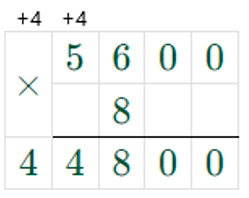
283040 : 10 ∙ 9 = 28304 ∙ 9 = 254736
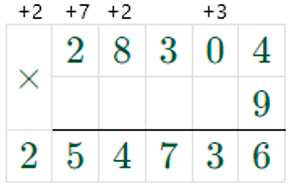
Номер 91.
Выполни деление с остатком. Сделай проверку.
Ответ:

1) Вспомни, как выполнять деление с остатком и делать проверку.
2) Вспомни, как выполнять деление многозначных чисел.
Вычисляем.
962 : 6 = 160 (ост. 2)
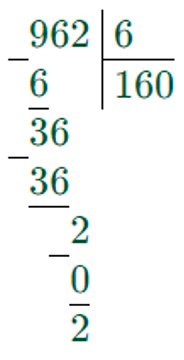
Делим по разрядам, слева направо.
Делим сотни:
9 : 6 = 1 (ост. 3)
В частное пишем 1 сот., а остаток уходит в десятки.
Делим десятки:
В остатке осталось 3 сот. = 30 дес.
В делимом в разряде десятков 6, получаем 30 + 6 = 36
36 : 6 = 6
В частном пишем 6 дес.
Делим единицы:
2 : 6 = 0 (ост. 2)
В частном пишем 0 ед.
Остаток – 2.
7286 : 7 = 1040 (ост. 6)
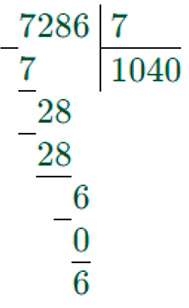
Делим по разрядам, слева направо.
Делим тысячи:
7 : 7 = 1
В частное пишем 1 тыс.
Делим сотни:
2 : 7 = 0 (ост. 2)
В частное пишем 0 сот., а остаток уходит в десятки.
Делим десятки:
В остатке осталось 2 сот. = 20 дес.
В делимом в разряде десятков 8, получаем 20 + 8 = 28
28 : 7 = 4
В частном пишем 4 дес.
Делим единицы:
6 : 7 = 0 (ост. 6)
В частном пишем 0 ед.
Остаток – 6.
56647 : 8 = 7080 (ост. 7)
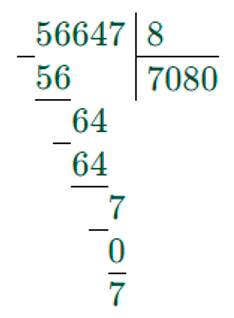
Делим по разрядам, слева направо.
Делим десятки тысяч:
5 : 8 = 0 (ост. 5)
В частное ничего не пишем, а остаток уходит в сотни.
Делим тысячи:
В остатке осталась 5 дес.тыс. = 50 тыс.
В делимом в разряде тысячи 6, получаем 50 + 6 = 56
56 : 8 = 7
В частное пишем 7 тыс.
Делим сотни:
6 : 8 = 0 (ост. 6)
В частное пишем 0 сот., а остаток уходит в десятки.
Делим десятки:
В остатке осталось 6 сот. = 60 дес.
В делимом в разряде десятков 4, получаем 60 + 4 = 64
64 : 8 = 8
В частном пишем 8 дес.
Делим единицы:
7 : 6 = 0 (ост. 7)
В частном пишем 0 ед.
Остаток – 7.
Делаем проверку.
962 : 6 = 160 (ост. 2)
Проверка:
1) 2 < 6
2) 160 ∙ 6 = 960
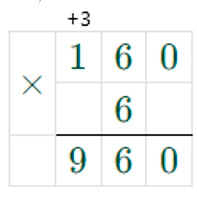
3) 960 + 2 = 962
7286 : 7 = 1040 (ост. 6)
Проверка:
1) 6 < 7
2) 1040 ∙ 7 = 7280
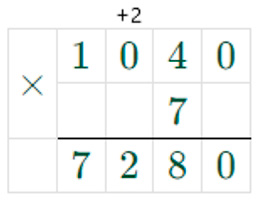
3) 7280 + 6 = 7286
56647 : 8 = 7080 (ост. 7)
Проверка:
1) 7 < 8
2) 7080 ∙ 8 = 56640
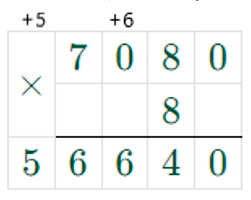
3) 56640 + 7 = 56647
Оформляем задание в тетрадь.

Номер 92.
Начерти такие фигуры и вырежи их.
1) Как можно убедиться в том, что каждая фигура симметрична? Выполни это.
2) Найди и сравни площади этих фигур.
3) Покажи, как из каждой фигуры, разрезав её на 2 части, можно сложить квадрат.
1) Это можно проверить сгибанием. Нужно сложить её пополам и если две части фигуры совместятся, то фигура симметрична.
Синяя линия – ось симметрии.

2) Площадь первой фигуры = 9 см2
Площадь второй фигуры = 4 см2
9 см2 > 4 см2
Площадь первой фигуры больше.
3)
.jpg)
1) Площадь фигуры – часть плоскости, занятая фигурой.
2) 1 см2 = 1 см ∙ 1 см
Начертим фигуры.
Начертим фигуры и вырежем их.
Проведём синей линией оси симметрии, которые показывают, что данные фигуры симметричны.
Это можно проверить сгибанием. Нужно сложить её пополам, и если две части фигуры совместятся, то фигура симметрична.
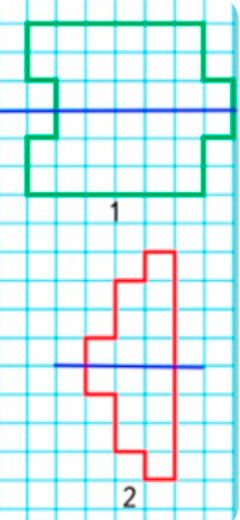
Рассуждаем.
Для того, чтобы найти площади этих фигур, надо посчитать количество клеточек внутри этой фигуры и разделить это количество на 4, так как 1 см2 соответствует площади четырёх клеточек:
Зелёная фигура – 36 клеточек.
36 : 4 = 9 (см2) – площадь зелёной фигуры.
Красная фигура – 16 клеточек.
16 : 4 = 4 (см2) – площадь красной фигуры.
9 см2 > 4 см2.
Значит, площадь зелёной фигуры больше, чем площадь красной фигуры.
Продолжаем рассуждения.
Разрежем каждую фигуру на две части так, чтобы при совмещении эти двух частей получился квадрат.
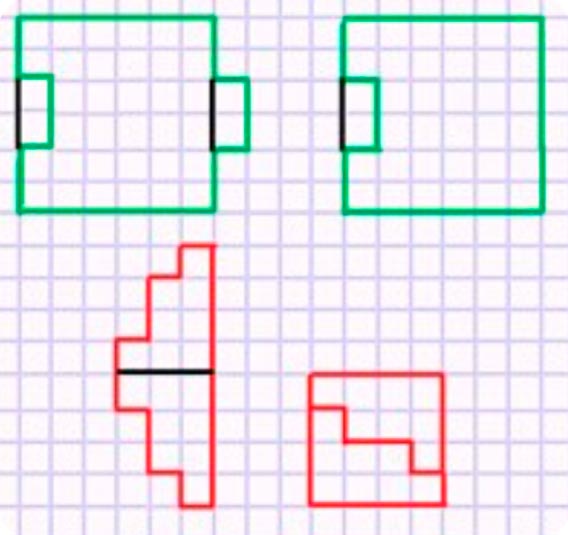
Задание внизу страницы
Вычисли.
Ответ:7200 : 90 = 80 9600 : 300 = 32
Помни, как разделить число на произведение.
Вычисляем.
7200 : 90 = 7200 : (9 ∙ 10) = 7200 : 10 : 9 = 720 : 9 = 80
Представим делитель 90 в виде произведения чисел 10 и 9, разделим число 7200 на первый множитель – 10, затем полученный результат разделим на второй множитель – 9.
Чтобы число разделить на 10, нужно справа отбросить один нуль.
9600 : 300 = 9600 : (3 ∙ 100) = 9600 : 100 : 3 = 96 : 3 = 32
Представим делитель 300 в виде произведения чисел 100 и 7, разделим число 9600 на первый множитель – 100, затем полученный результат разделим на второй множитель – 3.
Чтобы число разделить на 100, нужно справа отбросить два нуля.
Оформляем задание в тетрадь.
7200 : 90 = 7200 : (9 ∙ 10) = (7200 : 10) : 9 = 720 : 9 = 80
9600 : 300 = 9600 : (3 ∙ 100) = (9600 : 100) : 3 = 96 : 3 = 32
Задание на полях страницы
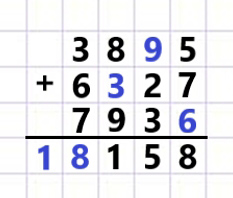
Ребус.

Ответ:

Вспомни, как складывать многозначные числа столбиком.
Рассмотрим ребус.

Сложили 3 слагаемых и получили сумму. Некоторые цифры этих слагаемых и суммы неизвестны.
Рассуждаем.
Многозначные числа складываются по разрядам справа налево, начиная с разряда единиц.
Рассмотрим разряд единиц.
В третьем слагаемом неизвестна цифра из разряда единиц.
Обозначим её за х, получим уранение:
5 + 7 + х = *8
х + 12 = *8
Сумма может быть только двузначным числом, заканчивающимся на 8, а х – только однозначным, значит
6 + 12 = 18
В сумме в единицах – 8, а 1 дес. запоминаем и прибавляем к десяткам.
х = 6 – цифра в разряде единиц третьего слагаемого.
Рассмотрим разряд десятков.
В первом слагаемом неизвестна цифра из разряда десятков.
Обозначим её за х, получим уранение:
х + 2 + 3 + 1 (запомнили) = *8
х + 6 = *5
Сумма может быть только двузначным числом, заканчивающимся на 5, а х – только однозначным, значит
9 + 6 = 15
В сумме в десятках – 5, а 1 сот. запоминаем и прибавляем к сотням.
х = 9 – цифра в разряде десятков первого слагаемого.
Рассмотрим разряд сотен.
Во втором слагаемом неизвестна цифра из разряда сотен.
Обозначим её за х, получим уранение:
8 + х + 9 + 1 (запомнили) = *1
х + 18 = *1
Сумма может быть только двузначным числом, заканчивающимся на 1, а х – только однозначным, значит
3 + 18 = 21
В сумме в сотнях – 1, а 2 тыс. запоминаем и прибавляем к тысячам.
х = 3 – цифра в разряде сотен второго слагаемого.
Рассмотрим разряд тысяч.
В сумме неизвестна цифра из разряда тысяч.
Обозначим её за х, получим уранение:
3 + 6 + 7 + 2 (запомнили) = х
х = 18
8 – цифра в разряде тысяч суммы.
1 – цифра в разряде десятков тысяч суммы.
Оформляем задание в тетрадь.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.