Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 22

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 20.
У хозяйки 3 корзины с яблоками. Всего в них 60 кг яблок. В первой и второй корзинах вместе 38 кг яблок, а во второй и третьей вместе 40 кг. Сколько килограммов яблок в каждой корзине?
Ответ:
1) 60 − 38 = 22 (кг) – яблок в третьей корзине.
2) 60 − 40 = 20 (кг) – яблок в первой корзине.
3) 60 − 20 − 22 = 18 (кг) – яблок во второй корзине.
Ответ: 20 кг яблок всего в первой корзине, 18 кг яблок всего во второй корзине, 22 кг яблок всего в третьей корзине.
Оформляем условие задачи в виде краткой записи.
Оформляем условие.
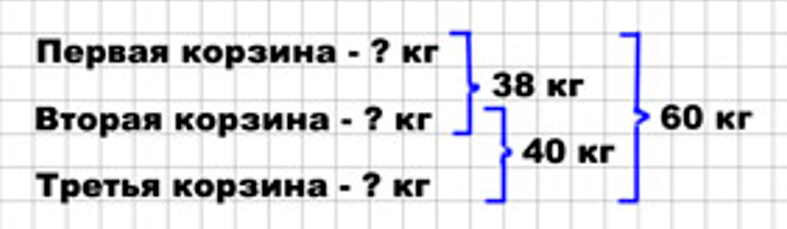
Рассуждаем.
Узнаем сколько яблок в третьей корзине, для этого из всего количества яблок вычтем количество яблок в первой и второй корзинах вместе.
1) 60 − 38 = 22 (кг) – яблок в третьей корзине.
Продолжаем рассуждение.
Узнаем сколько яблок в первой корзине, для этого из всего количества яблок вычтем количество яблок во второй и третьей корзинах вместе.
2) 60 − 40 = 20 (кг) – яблок в первой корзине.
Продолжаем рассуждение.
Узнаем сколько яблок во второй корзине, для этого из всего количества яблок вычтем количество яблок в первой и третьей корзинах вместе.
3) 60 − 20 − 22 = 18 (кг) – яблок во второй корзине.
Записываем ответ.
Ответ: 20 кг, 18 кг, 22 кг.
Номер 21.
Ответ:
Алгоритм записи и решения умножения на числа, оканчивающиеся нулями:
1) Записываем первый множитель.
2) Второй множитель записываем так, чтобы нули остались в стороне.
3) Умножаем многозначное число на число, не обращая внимания на нули.
4) К полученному результату приписываем эти нули.
5) Читаем ответ.
Выполняем вычисления по действиям.

Оставшиеся примеры решаем самостоятельно.
Оформляем задание в тетрадь.
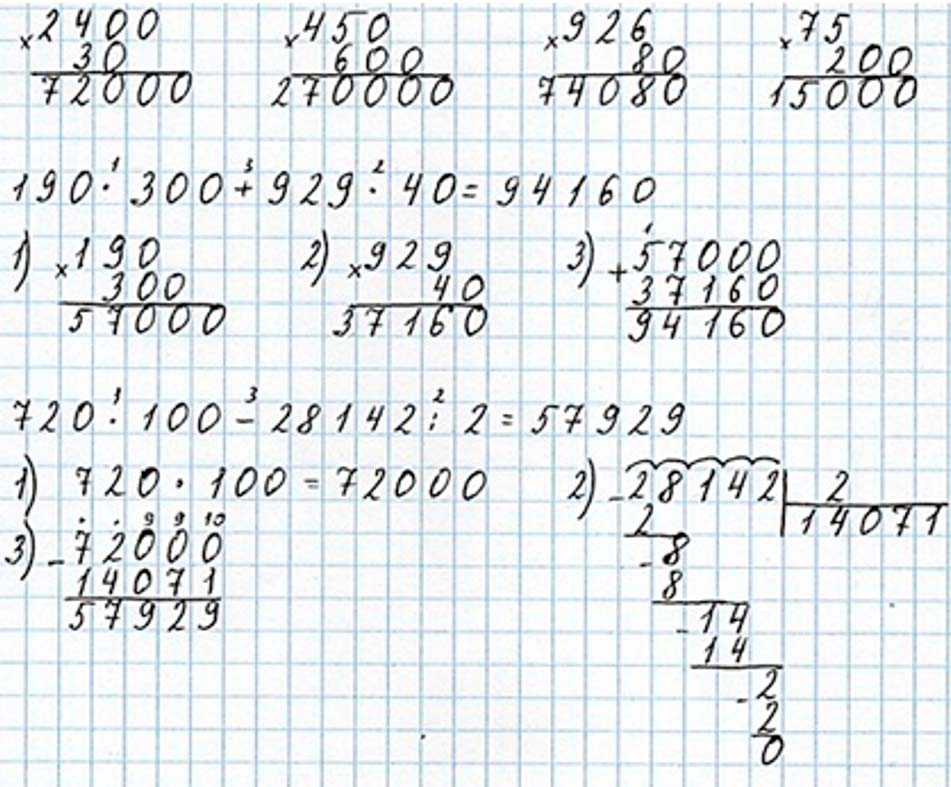
Номер 22.
Ответ:

Помним о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Выполняем вычисления по действиям.
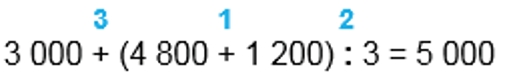
1) 4 800 + 1 200 = 6 000
2) 6 000 : 3 = 2 000
3) 3 000 + 2 000 = 5 000
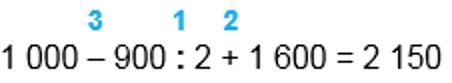
1) 900 : 2 = 450
2) 1 000 – 450 = 550


Оформляем задание в тетрадь.

Номер 23.
Вычисли значение выражения а ∙ d, если: 1) а = 8090 и d = 90; 2) а = 108347 и d = 6.
Ответ:1) a ∙ d, если а = 8090, d = 90, то

2) a ∙ d, если а = 108347, d = 6, то

Алгоритм записи и решения умножения на числа, оканчивающиеся нулями:
1) Записываем первый множитель.
2) Второй множитель записываем так, чтобы нули остались в стороне.
3) Умножаем многозначное число на число, не обращая внимания на нули.
4) К полученному результату приписываем эти нули.
5) Читаем ответ.
Выполним вычисления при а = 8 090 и b = 90.
1) a ∙ d, если а = 8090, d = 90, то
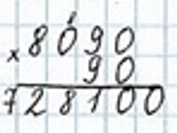
Выполним вычисления при а = 108 347 и b = 6.
2) a ∙ d, если а = 108347, d = 6, то

Оформим задание в тетрадь.
Номер 24.
В новом студенческом общежитии 20 трёхкомнатных квартир, 40 двухкомнатных и 4 однокомнатные. Сколько студентов в общежитии, если у каждого из них отдельная комната?
Ответ:
Трёхкомнатные – 20 кв.
Двухкомнатные – 40 кв.
Однокомнатные – 4 кв.
Всего – ?
1) 3 · 20 = 60 (к.) – в трёхкомнатных квартирах.
2) 2 · 40 = 80 (к.) – в двухкомнатных квартирах.
3) 1 · 4 = 4 (к.) – в однокомнатных квартирах.
4) 60 + 80 + 4 = 144 (ст.) – в общежитии.
Ответ: 144 студента всего в общежитии.
Оформляем условие задачи в виде таблицы.
Оформляем условие.
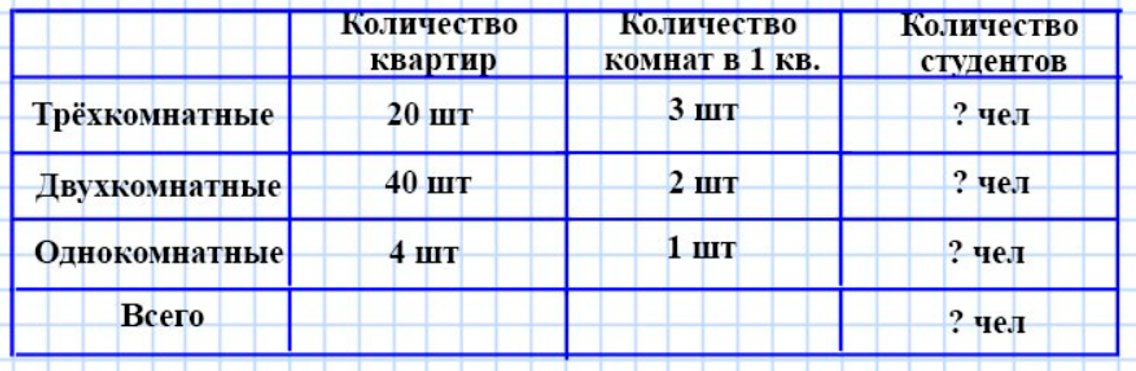
Рассуждаем.
Узнаем, сколько студентов проживает в трехкомнатных квартирах. Для этого количество квартир умножим на количество комнат.
1) 20 ∙ 3 = 60 (чел.) – проживает в трехкомнатных квартирах.
Продолжаем рассуждение.
Узнаем, сколько студентов проживает в двухкомнатных квартирах. Для этого количество квартир умножим на количество комнат.
2) 40 ∙ 2 = 80 (чел.) – проживает в двухкомнатных квартирах.
Продолжаем рассуждение.
Узнаем, сколько студентов проживает в однокомнатных квартирах. Для этого количество квартир умножим на количество комнат.
3) 4 ∙ 1 = 4 (чел.) – проживает в однокомнатных квартирах.
Продолжаем рассуждение.
Узнаем, сколько всего студентов проживает в общежитии.
4) 60 + 80 + 4 = 144 (чел.)
Записываем ответ.
Ответ: 144 студента проживает в общежитии.
Номер 25.
Директор предприятия часто ведёт международные переговоры по телефону. Одна минута разговора с Белоруссией стоит a р., с Францией – а ∙ 3 р., с Китаем – а ∙ 5 р. Состоялось 6 разговоров с Белоруссией, 4 разговора с Францией и 2 разговора с Китаем. Продолжительность каждого разговора 5 мин. Составь различные выражения по этому условию и поясни, что они означают.
Ответ:а ∙ 5 – стоимость одного разговора с Белоруссией. а ∙ 3 ∙ 5 – стоимость одного разговора с Францией. а ∙ 5 ∙ 5 – стоимость одного разговора с Китаем. а ∙ 6 ∙ 5 – стоимость разговоров за месяц с Белоруссией. а ∙ 3 ∙ 4 ∙ 5 – стоимость разговоров за месяц с Францией. а ∙ 5 ∙ 2 ∙ 5 – стоимость разговоров за месяц с Китаем.
Оформляем условие задачи в виде таблицы.
Оформляем условие.
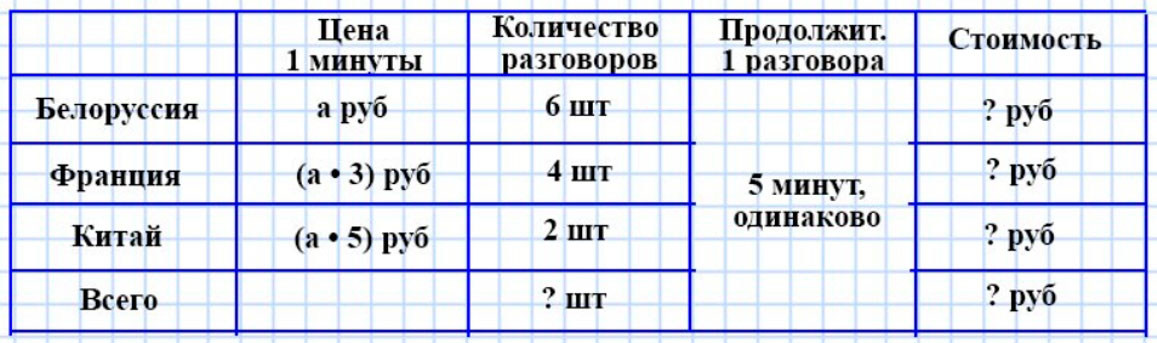
Составляем выражения по данному условию с пояснениями.
1) а ∙ 5 – стоимость одного разговора с Белоруссией.
2) а ∙ 3 ∙ 5 – стоимость одного разговора с Францией.
3) а ∙ 5 ∙ 5 – стоимость одного разговора с Китаем.
4) а ∙ 6 ∙ 5 – стоимость разговоров за месяц с Белоруссией.
5) а ∙ 3 ∙ 4 ∙ 5 – стоимость разговоров за месяц с Францией.
6) а ∙ 5 ∙ 2 ∙ 5 – стоимость разговоров за месяц с Китаем.
Номер 26.
За 6 табуреток заплатили а р., а за 4 стула – b р.
1) Поставь к этому условию два разных вопроса, чтобы задача решалась так: b : 4 − а : 6; (b : 4) : (а : 6).
2) Найди значение каждого выражения при а = 1200 р. и b = 3200 р.
1) b : 4 − a : 6 – на сколько дороже стул табуретки.
(b : 4) : (a : 6) – во сколько раз больше стоит стул, чем табуретка.
2) b : 4 − а : 6 = 3200 : 4 − 1200 : 6 = 800 − 200 = 600
(b : 4) : (a : 6) = (3200 : 4) : (1200 : 6) = 800 : 200 = 4
Оформляем условие задачи в виде таблицы.
Оформляем условие.

Ставим вопросы к задаче, чтобы она решалась данными выражениями.
b : 4 − a : 6 – на сколько дороже стул табуретки.
(b : 4) : (a : 6) – во сколько раз больше стоит стул, чем табуретка.
Найдем значение каждого выражения при а = 1200 р. и b = 3200 р.
1) b : 4 − а : 6 = 3200 : 4 − 1200 : 6 = 800 − 200 = 600 (рублей) – один стул дороже одной табуретки.
2) (b : 4) : (a : 6) = (3200 : 4) : (1200 : 6) = 800 : 200 = 4 (раз) – один стул дороже одной табуретки.
Записываем ответ.
Ответ: один стул дороже одной табуретки на 600 рублей или в 4 раза.
Номер 27.
Журнал объявил конкурс детских рисунков, в котором приняла участие одна девятая часть его подписчиков. Сколько подписчиков у журнала, если редакция получила рисунки от 10000 детей?
Ответ:
10000 ∙ 9 = 90000 (чел.)
Ответ: 90000 подписчиков у журнала.
Оформляем условие задачи в виде схематического чертежа.
Оформляем условие.
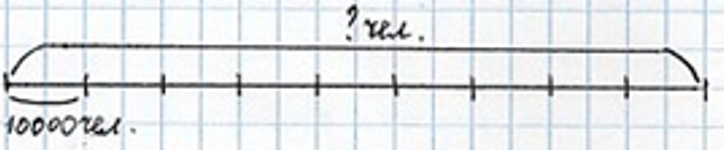
Рассуждаем.
Чтобы узнать, сколько подписчиков у журнала, нужно количество детей, принявших участие в конкурсе, умножить на 9. Так как нам известно, что в конкурсе детских рисунков приняла участие девятая часть от всех подписчиков.
10000 ∙ 9 = 90000 (чел.)
Записываем ответ.
Ответ: 90000 подписчиков у журнала.
Номер 28.
Найди ошибки в решении уравнений.
Ответ:
376 − х = 7 ∙ 9
376 − х = 63
х = 376 − 63
х = 313
Проверка:
376 - 313 = 7 * 9
63 = 63
Ответ: х = 313
у : 3 = 720 : 9
у : 3 = 80
у = 80 ∙ 3
у = 240
Проверка:
240 : 3 = 720 : 9
80 = 80
Ответ: у = 240
90 : х = 15 * 6
90 : х = 90
х = 90 : 90
х = 1
Проверка:
90 : 1 = 15 * 6
90 = 90
Ответ: х = 1
Уравнение – равенство с неизвестной, при подстановке числа в которую, получается верное равенство.
Вспомни названия компонентов действия умножения, и зависимость между компонентами и результатом действия умножения:
1 множитель ∙ 2 множитель = значение произведения.
Значение произведения : 1 множитель = 2 множитель.
Значение произведения : 2 множитель = 1 множитель.
Уменьшаемое – вычитаемое = значение разности.
Уменьшаемое – значение разности = вычитаемое.
Значение разности + вычитаемое = уменьшаемое.
Делимое : делитель = значение разности.
Делимое : значение разности = делитель.
Значение разности ∙ делитель = делимое.
Найдем ошибки в решении уравнений.

Оформим задание в тетрадь, исправляя ошибки.
376 − х = 7 ∙ 9
376 − х = 63
х = 376 − 63
у : 3 = 720 : 9
у = 80 ∙ 3
90 : х = 15 ∙ 6
х = 90 : 90
Задание на полях страницы
Начерти и раскрась узор
Ответ:
Чтобы проще было перечертить узор, проведи оси симметрии.
Начертим и раскрасим узор.
Внимательно рассмотри узор на полях страницы, подготовь необходимые инструменты и перечерти его в тетрадь.
Оформим задание в тетрадь.
Что узнали. Чему научились
Номер 1.
Объясни приём вычисления.
18 ∙ 20 = 18 ∙ (2 ∙ 10) = (18 ∙ 2) ∙ 10 = 36 ∙ 10 = 360
25 ∙ 12 = 25 ∙ (4 ∙ 3) = (25 ∙ 4) ∙ 3 = 100 ∙ 3 = 300
Перестановка и группировка множителей.
1) От перестановки множителей произведение не изменяется.
2) Два соседних множителя можно заменять их произведением.
3) Помни, как умножить число на произведение.
Рассмотрим данные примеры.
18 ∙ 20 = 18 ∙ (2 ∙ 10) = (18 ∙ 2) ∙ 10 = 36 ∙ 10 = 360
25 ∙ 12 = 25 ∙ (4 ∙ 3) = (25 ∙ 4) ∙ 3 = 100 ∙ 3 = 300
Объясним приемы вычисления.
В примерах один из множителей был разбит на два множителя, а затем, перегруппировав полученные множители, было выполнено умножение. Для решения применялось свойство умножения: «От перестановки множителей произведение не изменяется».
Номер 2.
Закончи решение.
Ответ:
1) 35 ∙ 20 = 35 ∙ (2 ∙ 10) = (35 ∙ 2) ∙ 10 = 700
25 ∙ 24 = 25 ∙ (4 ∙ 6) = (25 ∙ 4) ∙ 6 = 600
2) 16 ∙ 30 = 16 ∙ (3 ∙ 10) = (16 ∙ 3) ∙ 10 = 480
42 ∙ 20 = 42 ∙ (2 ∙ 10) = (42 ∙ 2) ∙ 10 = 840
12 ∙ 40 = 12 ∙ (4 ∙ 10) = ( 12 ∙ 4) ∙ 10 = 480
25 ∙ 16 = 5 ∙ 5 ∙ 2 ∙ 8 = (5 ∙ 2) ∙ (5 ∙ 8) = 10 ∙ 40 = 400
15 ∙ 18 = 3 ∙ 5 ∙ 2 ∙ 9 = (5 ∙ 2) ∙ (3 ∙ 9) = 10 ∙ 27 = 270
45 ∙ 14 = 9 ∙ 5 ∙ 2 ∙ 7 = (5 ∙ 2) ∙ (9 ∙ 7) = 10 ∙ 63 = 630
13 ∙ 60 = 13 ∙ (6 ∙ 10) = (13 ∙ 6) ∙ 10 = 780
45 ∙ 20 = 45 ∙ (2 ∙ 10) = (45 ∙ 2) ∙ 10 = 900
15 ∙ 30 = 15 ∙ (3 ∙ 10) = (15 ∙ 3) ∙ 10 = 450
14 ∙ 50 = 2 ∙ 7 ∙ 5 ∙ 10 = (2 ∙ 5) ∙ (7 ∙ 10) = 700
1) От перестановки множителей произведение не изменяется.
2) Два соседних множителя можно заменять их произведением.
3) Помни, как умножить число на произведение.
Рассуждаем и вычисляем.
Используем сочетательное свойство: два соседних множителя можно заменить их произведением.
Удобно группировать множители так, чтобы хотя бы один из множителей был круглым числом.
35 ∙ 20 = 35 ∙ (2 ∙ 10) = (35 ∙ 2) ∙ 10 = 70 ∙ 10 = 700
Представим число 20 в виде произведения двух чисел 2 и 10. Сгруппируем множители для удобства и вычислим.
25 ∙ 24 = 25 ∙ (4 ∙ 6) = (25 ∙ 4) ∙ 6 = 100 ∙ 6 = 600
Представим число 24 в виде произведения двух чисел 4 и 6. Сгруппируем множители для удобства и вычислим.
16 ∙ 30 = 16 ∙ (3 ∙ 10) = (16 ∙ 3) ∙ 10 = 48 ∙ 10 = 480
Представим число 30 в виде произведения двух чисел 3 и 10. Сгруппируем множители для удобства и вычислим.
42 ∙ 20 = 42 ∙ (2 ∙ 10) = (42 ∙ 2) ∙ 10 = 84 ∙ 10 = 840
Представим число 20 в виде произведения двух чисел 2 и 10. Сгруппируем множители для удобства и вычислим.
12 ∙ 40 = 12 ∙ (4 ∙ 10) = (12 ∙ 4) ∙ 10 = 48 ∙ 10 = 480
Представим число 40 в виде произведения двух чисел 4 и 10. Сгруппируем множители для удобства и вычислим.
25 ∙ 16 = 5 ∙ 5 ∙ 2 ∙ 8 = (5 ∙ 8) ∙ (5 ∙ 2) = 40 ∙ 10 = 400
Представим число 25 в виде произведения двух чисел 5 и 5, а число 16 в виде произведения двух чисел 2 и 8. Сгруппируем множители для удобства и вычислим.
15 ∙ 18 = 3 ∙ 5 ∙ 2 ∙ 9 = (3 ∙ 9) ∙ (5 ∙ 2) = 27 ∙ 10 = 270
Представим число 15 в виде произведения двух чисел 3 и 5, а число 18 в виде произведения двух чисел 2 и 9. Сгруппируем множители для удобства и вычислим.
45 ∙ 14 = 9 ∙ 5 ∙ 2 ∙ 7 = (9 ∙ 7) ∙ (5 ∙ 2) = 63 ∙ 10 = 630
Представим число 45 в виде произведения двух чисел 9 и 5, а число 14 в виде произведения двух чисел 2 и 7. Сгруппируем множители для удобства и вычислим.
13 ∙ 60 = 13 ∙ (6 ∙ 10) = (13 ∙ 6) ∙ 10 = 78 ∙ 10 = 780
Представим число 60 в виде произведения двух чисел 6 и 10. Сгруппируем множители для удобства и вычислим.
45 ∙ 20 = 45 ∙ (2 ∙ 10) = (45 ∙ 2) ∙ 10 = 90 ∙ 10 = 900
Представим число 20 в виде произведения двух чисел 2 и 10. Сгруппируем множители для удобства и вычислим.
15 ∙ 30 = 15 ∙ (3 ∙ 10) = (15 ∙ 3) ∙ 10 = 45 ∙ 10 = 450
Представим число 30 в виде произведения двух чисел 3 и 10. Сгруппируем множители для удобства и вычислим.
14 ∙ 50 = 2 ∙ 7 ∙ 5 ∙ 10 = (7 ∙ 10) ∙ (2 ∙ 5) = 70 ∙ 10 = 700
Представим число 14 в виде произведения двух чисел 2 и 7, а число 50 в виде произведения двух чисел 5 и 10. Сгруппируем множители для удобства и вычислим.
Оформим задание в тетрадь.
1) 35 ∙ 20 = 35 ∙ 2 ∙ 10 = 70 ∙ 10 = 700
25 ∙ 24 = 25 ∙ 4 ∙ 6 = 100 ∙ 6 = 600
2) 16 ∙ 30 = 16 ∙ 3 ∙ 10 = 48 ∙ 10 = 480
42 ∙ 20 = 42 ∙ 2 ∙ 10 = 84 ∙ 10 = 840
12 ∙ 40 = 12 ∙ 4 ∙ 10 = 48 ∙ 10 = 480
25 ∙ 16 = 5 ∙ 5 ∙ 2 ∙ 8 = 40 ∙ 10 = 400
15 ∙ 18 = 3 ∙ 5 ∙ 2 ∙ 9 = 27 ∙ 10 = 270
45 ∙ 14 = 9 ∙ 5 ∙ 2 ∙ 7 = 63 ∙ 10 = 630
13 ∙ 60 = 13 ∙ 6 ∙ 10 = 78 ∙ 10 = 780
45 ∙ 20 = 45 ∙ 2 ∙ 10 = 90 ∙ 10 = 900
15 ∙ 30 = 15 ∙ 3 ∙ 10 = 45 ∙ 10 = 450
14 ∙ 50 = 2 ∙ 7 ∙ 5 ∙ 10 = 70 ∙ 10 = 700
Номер 3.
Сравни выражения и поставь знак >, < или =, чтобы получились верные записи.
Ответ:
18 ∙ 40 = 18 ∙ 4 ∙ 10
18 ∙ 40 = 18 ∙ 40
72 ∙ 14 < 72 ∙ 10 ∙ 4
72 ∙ 14 < 72 ∙ 40
36 ∙ 5 ∙ 10 > 36 ∙ 15
36 ∙ 50 > 36 ∙ 15
98 ∙ 21 = 98 ∙ 3 ∙ 7
98 ∙ 21 = 98 ∙ 21
«>» – знак «больше»
«<» – знак «меньше»
«=» – знак «равно»
Рассуждаем.
Рассмотрим выражения 18 ∙ 40 и 18 ∙ 4 ∙ 10
Сравним поочерёдно множители этих выражений.
18 = 18
4 ∙ 10 = 40
40 = 40
18 ∙ 40 = 18 ∙ 40
Значит, 18 ∙ 40 = 18 ∙ 4 ∙ 10
Рассмотрим выражения 72 ∙ 14 и 72 ∙ 10 ∙ 4
Сравним поочерёдно множители этих выражений.
72 = 72
10 ∙ 4 = 40
14 < 40
72 ∙ 14 < 72 ∙ 40
Значит, 72 ∙ 14 < 72 ∙ 10 ∙ 4
Рассмотрим выражения 36 ∙ 5 ∙ 10 и 36 ∙ 15
Сравним поочерёдно множители этих выражений.
36 = 36
5 ∙ 10 = 50
50 > 15
36 ∙ 50 > 36 ∙ 15
Значит, 36 ∙ 5 ∙ 10 > 36 ∙ 15
Рассмотрим выражения 98 ∙ 21 и 98 ∙ 3 ∙ 7
Сравним поочерёдно множители этих выражений.
98 = 98
3 ∙ 7 = 21
21 = 21
98 ∙ 21 = 98 ∙ 21
Значит, 98 ∙ 21 = 98 ∙ 3 ∙ 7
Оформим задание в тетрадь.
18 ∙ 40 = 18 ∙ 4 ∙ 10
18 ∙ 40 = 18 ∙ 40
72 ∙ 14 < 72 ∙ 10 ∙ 4
72 ∙ 14 < 72 ∙ 40
36 ∙ 5 ∙ 10 > 36 ∙ 15
36 ∙ 50 > 36 ∙ 15
98 ∙ 21 = 98 ∙ 3 ∙ 7
98 ∙ 21 = 98 ∙ 21
Номер 4.
Для ремонта квартиры купили 8 рулонов обоев длиной по 10 м 50 см. После ремонта осталась одна четвёртая часть купленных обоев. Сколько метров обоев осталось? Сколькими способами можно решить задачу? Запиши каждое решение.
Задачу можно решить двумя способами.

Можно оформить в виде чертежа:

1-й способ решения:
1) 10 м 50 см ∙ 8 = 84 (м) – было куплено обоев. 2) 84 : 4 = 21 (м) – обоев осталось.
2-й способ решения:1) 8 : 4 = 2 (р.) – обоев осталось после ремонта.
2) 10 м 50 см ∙ 2 = 21 (м) – обоев осталось после ремонта.
Ответ: 21 м обоев всего остался после ремонта.
Оформляем условие задачи в виде краткой записи или схематического чертежа.
Задачу можно решить двумя способами.
Оформляем краткую запись.
Всего – 8 р. по 10 м 50 см
Осталось – 1/4 часть – ? м
или
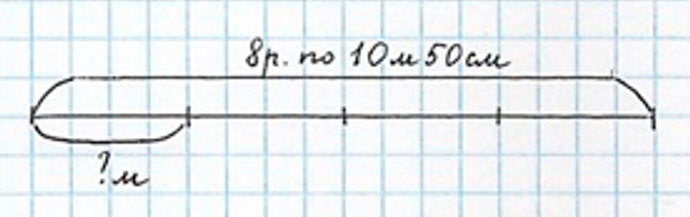
Шаг 1.
Рассуждаем.
Узнаем, сколько всего было куплено метров обоев, для этого количество метров одного рулона умножаем на количество рулонов.
10 м 50 см = 1000 см + 50 м = 1050 см
1050 ∙ 8 = 105 ∙ 10 ∙ 8 = (100 + 5) ∙ 8 ∙ 10 = (800 + 40) ∙ 10 = 8400 (см)
8400 см = 84 м – обоев было куплено.
Продолжаем рассуждение.
Узнаем, сколько метров обоев осталось, для этого все количество обоев делим на 4, потому что известно, что осталась одна четвертая часть.
84 : 4 = 21 (м) – обоев осталось.
Записываем ответ.
Ответ: 21 м обоев осталось.
Шаг 1.
Рассуждаем.
Узнаем, сколько рулонов обоев осталось после ремонта, для этого количество всех рулонов делим на 4, потому что известно, что осталась одна четвертая часть.
8 : 4 = 2 (р.) – обоев осталось.
Продолжаем рассуждение.
Узнаем, сколько метров обоев осталось после ремонта, для этого количество метров обоев в одном рулоне умножаем на количество оставшихся рулонов.
10 м 50 см = 1000 см + 50 м = 1050 см
1050 ∙ 2 = 105 ∙ 10 ∙ 2 = (100 + 5) ∙ 2 ∙ 10 = (200 + 10) ∙ 10 = 2100 (см)
2100 см = 21 м – обоев осталось.
Записываем ответ.
Ответ: 21 м обоев осталось.
Номер 5.
Школьная библиотека получила 290 новых учебников в одинаковых пачках. Учебников по русскому языку было 10 пачек, столько же пачек учебников по чтению и 9 пачек учебников по математике. Объясни, что показывают выражения.
Ответ:290 : (10 + 10 + 9) = 10 – количество учебников в одной пачке. 290 : (10 + 10 + 9) ∙ 9 = 90 – количество учебников по математике.
1) Помни о зависимости между компонентами и результатом действия деления.
2) Помни о том, каков конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а ∙ b, а – первый множитель, b – количество множителей.
3) Помни о зависимости между компонентами и результатом действия умножения.
Оформляем условие.
Всего – 290 новых учебников в одинаковых пачках
Русский язык – 10 пачек
Чтение – 10 пачек
Математика – 9 пачек
Рассуждаем.
Найдём общее количество пачек, для этого сложим все пачки по всем предметам.
10 + 10 + 9 = 29 (п.) – было всего.
Продолжаем рассуждение.
Если разделить общее количество учебников на общее количество пачек, то найдём количество учебников в одной пачке.
290 : 29 = 10 (уч.) – количество учебников в одной пачке.
Значит, выражение 290 : (10 + 10 + 9) показывает количество учебников в одной пачке.
Продолжаем рассуждение.
Если количество учебников в одной пачке умножить на 9, то узнаем, сколько новых учебников по математике получила школьная библиотека.
10 ∙ 9 = 90 (уч.) – новых по математике.
Значит, выражение 290 : (10 + 10 + 9) ∙ 9 показывает количество новых учебников по математике.
Записываем ответ.
290 : (10 + 10 + 9) = 10 – количество учебников в одной пачке;
290 : (10 + 10 + 9) ∙ 9 = 90 – количество новых учебников по математике.
Номер 6.
Ответ:
1) Помним о порядке выполнения арифметических действий, и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем, действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Вычисляем.
Расставляем порядок действий и вычисляем по действиям.
(852004 − (4560 + 27540 ∶ 5) = 841936
Первым действием выполним – деление, вторым – сложение и последним – вычитание.
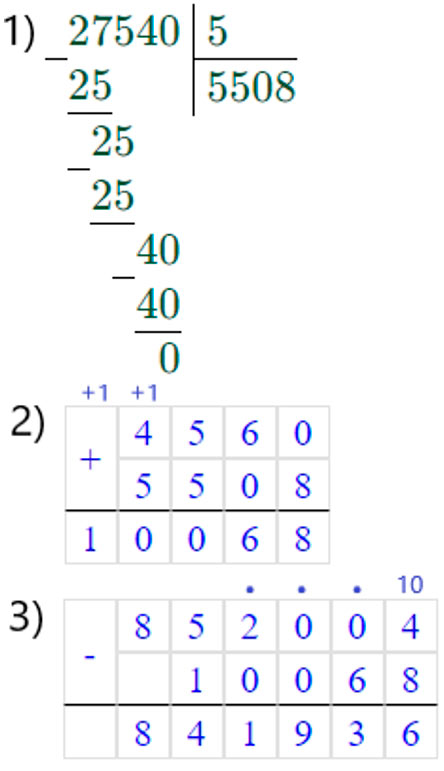
(690108 − (9382 ∙ 6 + 3126 ∶ 3) = 632774
Первым действием выполним – умножение, вторым – деление, третьим - сложение и последним – вычитание.
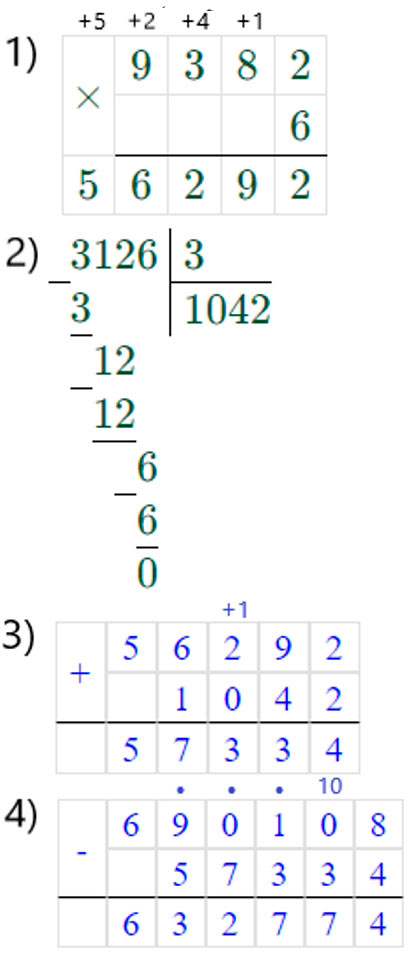
Группируем множители и вычисляем.
200 ∙ 15 ∙ 4 ∙ 5 = (200 ∙ 5) ∙ (15 ∙ 4) = 1000 ∙ 60 = 60000
12 ∙ 5 ∙ 250 ∙ 4 = (12 ∙ 5) ∙ (250 ∙ 4) = 60 ∙ 1000 = 60000
Оформляем задание в тетрадь.
852004 – (4560 + 27540 : 5) = 852004 – (4560 + 5508) = 852004 – 10068 = 841936
690108 – (9382 ∙ 6 + 3126 : 3) = 690108 – (56292 + 1042) = 690108 – 57334 = 632774
200 ∙ 15 ∙ 4 ∙ 5 = (200 ∙ 5) ∙ (15 ∙ 4) = 1000 ∙ 60 = 60000
12 ∙ 5 ∙ 250 ∙ 4 = (12 ∙ 5) ∙ (250 ∙ 4) = 60 ∙ 1000 = 60000
Номер 7.
Рассмотри таблицу и объясни, что обозначают выражения. 1) 30 : 5; 2) 400 : 100; 3) 100 : 5; 4) 100 − 5; 5) 30 : 5 + 400 : 100; 6) 30 : 5 − 400 : 200.

1) Время движения первого объекта. 2) Время движения второго объекта. 3) Во сколько раз скорость второго объекта больше скорости первого. 4) На сколько км/ч скорость второго объекта больше скорости первого. 5) Общее время движения обоих объектов. 6) На сколько больше был в движении первый объект, чем второй.
1) Чтобы найти расстояние, надо скорость умножить на время.
2) Чтобы найти скорость, надо расстояние разделить на время.
3) Чтобы найти время, надо расстояние разделить на скорость.
Рассмотрим таблицу.

Рассуждаем.
Рассмотрим выражение 30 : 5
30 – это расстояние
5 – это скорость
Если расстояние разделить на скорость, то получится время.
Значит, выражение 30 : 5 обозначает время движения первого объекта.
Рассмотрим выражение 400 : 100
400 – это расстояние
100 – это скорость
Если расстояние разделить на скорость, то получится время.
Значит, выражение 400 : 100 обозначает время движения второго объекта.
Рассмотрим выражение 100 : 5
100 – это скорость
5 – это скорость
Если одну скорость разделить на другую скорость, то узнаем, во сколько раз одна скорость больше, чем другая скорость.
Значит, выражение 100 : 5 обозначает, во сколько раз скорость второго объекта больше, чем скорость первого объекта.
Рассмотрим выражение 100 – 5
100 – это скорость
5 – это скорость
Если из одной скорости вычесть другую скорость, то узнаем, на сколько одна скорость больше, чем другая скорость.
Значит, выражение 100 – 5 обозначает, на столько км/ч скорость второго объекта больше скорости первого.
Рассмотрим выражение 30 : 5 + 400 : 100
30 : 5 – время движения первого объекта
400 : 100 – время движения второго объекта
Если сложить время движения первого и второго объектов, то узнаем общее время движения обоих объектов.
Значит, выражение 30 : 5 + 400 : 100 обозначает общее время движения обоих объектов.
Рассмотрим выражение 30 : 5 – 400 : 100
30 : 5 – время движения первого объекта
400 : 100 – время движения второго объекта
Если из времени движения первого объекта вычесть время движения второго объекта, то узнаем, на сколько больше был в движении первый объект, чем второй.
Значит, выражение 30 : 5 – 400 : 100 обозначает, на сколько больше был в движении первый объект, чем второй.
Оформляем задание в тетрадь.
1) 30 : 5 – время движения первого объекта.
2) 400 : 100 – время движения второго объекта.
3) 100 : 5 – во столько раз скорость второго объекта больше скорости первого.
4) 100 – 5 – на столько км/ч скорость второго объекта больше скорости первого.
5) 30 : 5 + 400 : 100 – общее время движения обоих объектов.
6) 30 : 5 – 400: 100 – на сколько больше был в движении первый объект, чем второй.
Номер 8.
Выполни деление с остатком и проверку.
Ответ:

Вспомни, как выполняется деление с остатком.
Выполняем вычисления.
1436 : 9 = 159 (ост. 5)
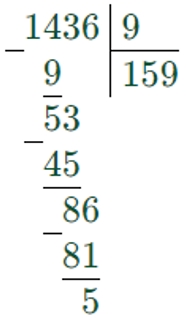
7365 : 8 = 920 (ост. 5)
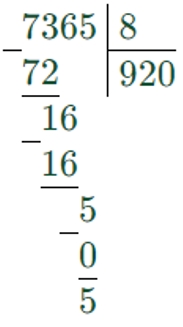
3506 : 7 = 500 (ост. 6)
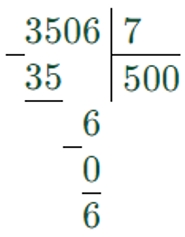
7251 : 5 = 1450 (ост. 1)
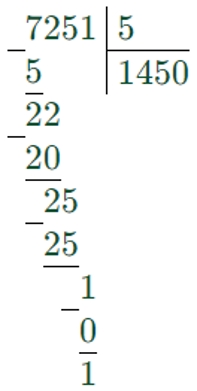
Делаем проверку.
1436 : 9 = 159 (ост. 5)
Проверка:
5 < 9
159 ∙ 9 = 1431
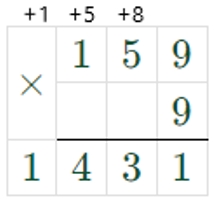
1431 + 5 = 1436
1436 = 1436
7365 : 8 = 920 (ост. 5)
Проверка:
5 < 8
920 ∙ 8 = 7360
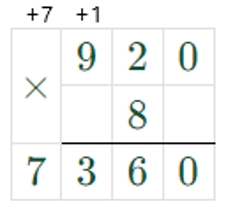
7360 + 5 = 7365
7365 = 7365
3506 : 7 = 500 (ост. 6)
Проверка:
6 < 7
500 ∙ 7 = 5 сот. ∙ 7 = 35 сот. = 3500
3500 + 6 = 3506
3506 = 3506
7251 : 5 = 1450 (ост. 1)
Проверка:
1 < 5
1450 ∙ 5 = 7250
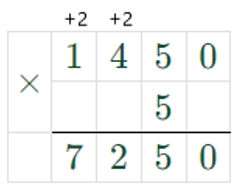
7250 + 1 = 7251
7251 = 7251
Оформляем задание в тетрадь.


Номер 9.
Ответ:


1) Помним о порядке выполнения арифметических действий.
2) Вспомни, как делить многозначные числа столбиком.
3) Вспомни, как складывать и вычитать многозначные числа столбиком.
Вычисляем.
Расставляем порядок действий и вычисляем по действиям.
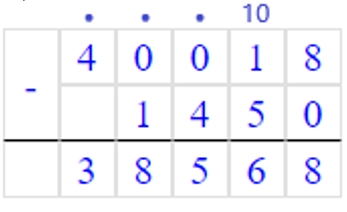
40018 − 725 ∙ 10 ∶ 5 = 38568
Сначала выполняем умножение и деление по порядку, а затем – вычитание.
1) 725 ∙ 10 = 7250
2) 7250 : 5 = 1450
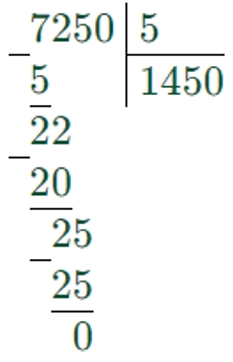
3) 40018 – 1450 = 38568
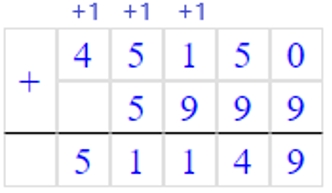
5999 + 903 ∙ 100 : 2 = 51149
Сначала выполняем умножение и деление по порядку, а затем – сложение.
1) 903 ∙ 100 = 90300
2) 90300 : 2 = 45150
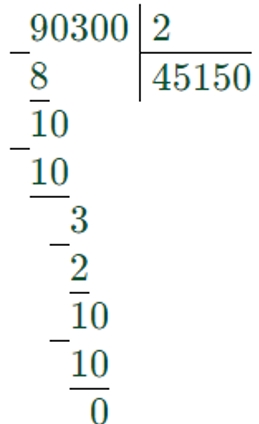
3) 5999 + 45150 = 51149
80115 : 3 ∙ 10 = 267050
Действия умножения и деления равнозначны, поэтому выполняем их по порядку – сначала деление, потом умножение.
1) 80115 : 3 = 26705
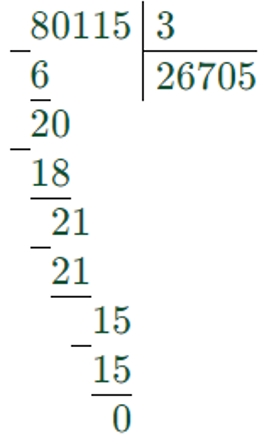
2) 26705 ∙ 10 = 267050
3152 : 8 ∙ 100 = 39400
Действия умножения и деления равнозначны, поэтому выполняем их по порядку – сначала деление, потом умножение.
1) 3152 : 8 = 394
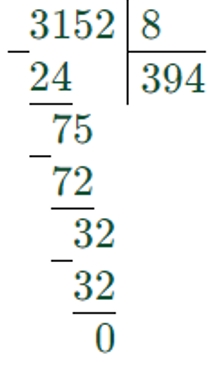
2) 394 ∙ 100 = 39400
8070 : 6 = 1345
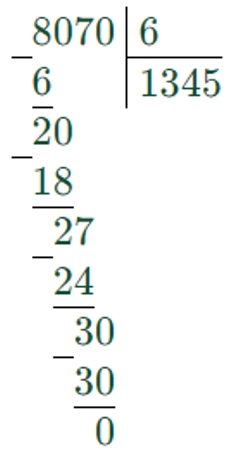
8070 ∙ 6 = 48420
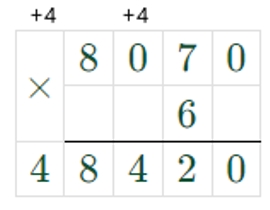
Оформляем задание в тетрадь.


Задания на полях страницы
Ребус.


Вспомни, как складывать многозначные числа столбиком.
Рассмотрим ребус.

Сложили 4 слагаемых и получили сумму. Некоторые цифры этих слагаемых неизвестны.
Рассуждаем.
Многозначные числа складываются по разрядам справа налево, начиная с разряда единиц.
Рассмотрим разряд единиц.
В втором слагаемом неизвестна цифра из разряда единиц.
Обозначим её за х, получим уранение:
8 + х + 7 + 9 = *0
х + 24 = *0
Сумма может быть только двузначным числом, заканчивающимся на 0, а х – только однозначным, значит
6 + 24 = 30
В сумме в единицах – 0, а 3 дес. запоминаем и прибавляем к десяткам.
х = 6 – цифра в разряде единиц второго слагаемого.
Рассмотрим разряд десятков.
В первом слагаемом неизвестна цифра из разряда десятков.
Обозначим её за х, получим уранение:
х + 6 + 4 + 7 + 3 (запомнили) = *8
х + 20 = *8
Сумма может быть только двузначным числом, заканчивающимся на 8, а х – только однозначным, значит
8 + 20 = 28
В сумме в десятках – 8, а 2 сот. запоминаем и прибавляем к сотням.
х = 8 – цифра в разряде десятков второго слагаемого.
Рассмотрим разряд сотен.
В третьем слагаемом неизвестна цифра из разряда сотен.
Обозначим её за х, получим уранение:
0 + 9 + х + 6 + 2 (запомнили) = *0
х + 17 = *0
Сумма может быть только двузначным числом, заканчивающимся на 0, а х – только однозначным, значит
3 + 17 = 20
В сумме в сотнях – 0, а 2 тыс. запоминаем и прибавляем к тысячам.
х = 3 – цифра в разряде сотен третьего слагаемого.
Рассмотрим разряд тысяч.
В четвёртом слагаемом неизвестна цифра из разряда тысяч.
Обозначим её за х, получим уранение:
1 + 2 + 1 + х + 2 (запомнили) = 10
х + 6 = 10
х = 10 – 6
х = 4 – цифра в разряде тысяч четвёртого слагаемого.
Оформим задание в тетрадь.

Реши. Найди лишнее уравнение.

х ∙ 8 = 56
х = 56 : 8
х = 7
Проверка:
7 ∙ 8 = 56
56 = 56
Ответ: х = 7
х ∙ 14 = 98
х = 98 : 14
х = 7
Проверка:
7 ∙ 14 = 98
98 = 98
Ответ: х = 7
84 : х = 12
х = 84 : 12
х = 7
Проверка:
84 ∙ 7 = 12
12 = 12
Ответ: х = 7
5 ∙ х = 35
х = 35 : 5
х = 7
Проверка:
5 ∙ 7 = 35
35 = 35
Ответ: х = 7
х ∙ 7 = 42
х = 42 : 7
х = 6
Проверка:
6 ∙ 7 = 42
42 = 42
Ответ: х = 6
Вывод: лишнее уравнение х · 7 = 42, потому что значение х в нём отличается от других и равно 6, а не 7.
1) Уравнение – равенство с неизвестной, при подстановке числа в которую, получается верное равенство.
2) Вспомни названия компонентов действия умножения, и зависимость между компонентами и результатом действия умножения.
Выполняем вычисления.
Решим все уравнения, чтобы определить лишнее.
х ∙ 8 = 56
х = 56 : 8
х = 7
Проверка:
7 ∙ 8 = 56
56 = 56
х ∙ 14 = 98
х = 98 : 14
х = 7
Проверка:
7 ∙ 14 = 98
98 = 98
84 : х = 12
х = 84 : 12
х = 7
Проверка:
84 : 7 = 12
12 = 12
5 ∙ х = 35
х = 35 : 5
х = 7
Проверка:
5 ∙ 7 = 35
35 = 35
х ∙ 7 = 42
х = 42 : 7
х = 6
Проверка:
6 ∙ 7 = 42
42 = 42
Записываем ответ.
Лишним является последнее уравнение х ∙ 7 = 42, так как у него х = 6, а во всех остальных уравнениях х = 7.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.