Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 111

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Прямоугольный параллелепипед
Номер 1.
1) Изготовь модель прямоугольного параллелепипеда, используя его развёртку (рис. 1). Вспомни план действий при изготовлении модели куба, составь план действий по изготовлению модели прямоугольного параллелепипеда и выполни его. Поверхность прямоугольного параллелепипеда состоит из прямоугольников, их называются гранями прямоугольного параллелепипеда. Стороны граней называют рёбрами, а вершины граней – вершинами прямоугольного параллелепипеда (рис. 2).
2) Сосчитай, сколько у прямоугольного параллелепипеда граней, сколько рёбер, сколько вершин.

1) План изготовления прямоугольного параллелепипеда:
Шаг 1: перенеси на клетчатую бумагу развертку.
Шаг 2 вырежи ее.
Шаг 3: прогни развертку по красным линиям сгиба.
Шаг 4: намажь клеем язычки для склеивания (обозначенные желтым цветом).
Шаг 5: склей модель.

2) У прямоугольного параллелепипеда – 6 граней, 12 рёбер и 8 вершин.
Повтори материал о прямоугольнике.
Рассмотрим модель прямоугольного параллелепипеда.
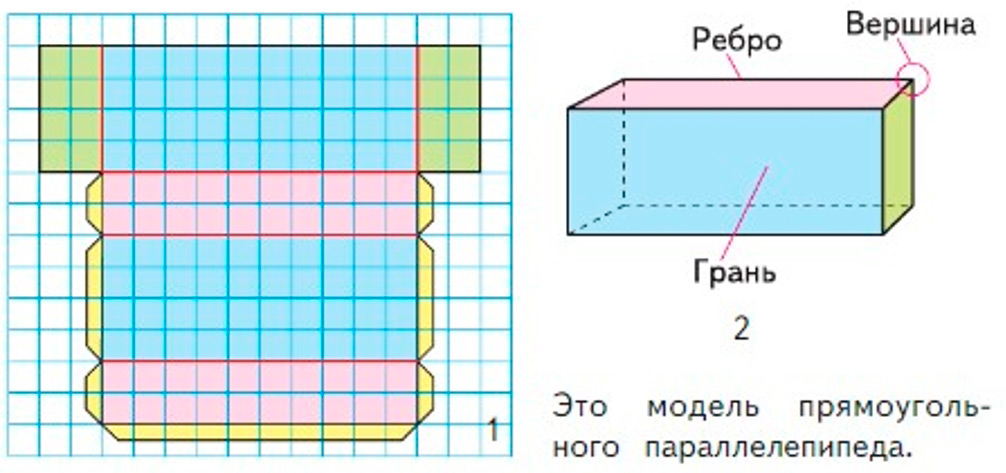
Изготовим по плану прямоугольный параллелепипед.
План изготовления прямоугольного параллелепипеда:
Шаг 1: перенеси на клетчатую бумагу развертку.
Шаг 2 вырежи ее.
Шаг 3: прогни развертку по красным линиям сгиба.
Шаг 4: намажь клеем язычки для склеивания (обозначенные желтым цветом).
Шаг 5: склей модель.

Сосчитаем количество граней, ребер и вершин параллелепипеда.
У прямоугольного параллелепипеда – 6 граней, 12 рёбер и 8 вершин.
Номер 2.
Является ли фигура (рис. 3) развёрткой прямоугольного параллелепипеда? Начерти такую фигуру в тетради. Дополни её так, чтобы она стала развёрткой прямоугольного параллелепипеда.

Нет, данная развертка не является разверткой прямоугольного параллелепипеда, потому что граней у него всего 6, а на представленной развертке – 5.

Повтори материал о прямоугольнике.
Рассмотрим фигуру и ответим на вопрос.
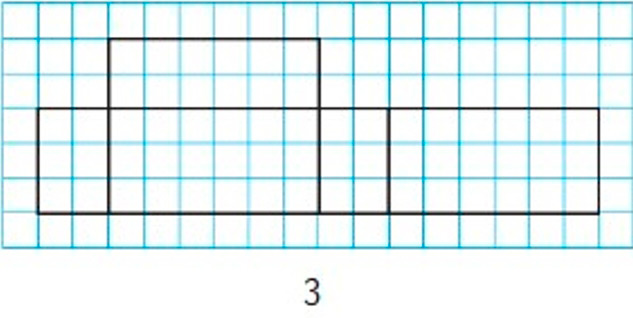
Нет, данная развертка не является разверткой прямоугольного параллелепипеда, потому что граней у него всего 6, а на представленной развертке – 5.
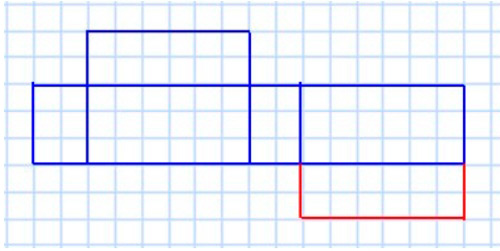
Начертим развертку прямоугольного параллелепипеда.
Номер 2.
Рассмотри чертёж. Назови диагонали квадрата и точку их пересечения. Что можно сказать о свойствах диагоналей квадрата, зная, что квадрат тоже прямоугольник? У диагоналей квадрата есть ещё одно свойство. При пересечении диагоналей квадрата получаются четыре прямых угла. Проверь это свойство по чертежу.

КМ и LN – диагонали квадрата, Е – точка их пересечения. Диагонали квадрата точкой пересечения делятся пополам.
Номер 3.
Используя свойства диагоналей квадрата, начерти в тетради квадрат, длина диагонали которого 5 см.
Ответ:
Номер 4.
Построить 4 прямых угла с общей вершиной можно и на нелинованной бумаге.
1) Отложи на прямой отрезок АВ. Радиусом, равным больше половины длины отрезка, проведи 2 окружности с центрами в точках А и В (чертёж 1). Обозначь точки пересечения окружностей буквами С и D. Проведи прямую через точки С и D. Точку пересечения прямых обозначь буквой О. Проверь, что все 4 угла с вершиной в точке О прямые.
Вместо окружностей можно проводить дуги (части окружностей) любого радиуса, который всегда должен быть больше половины длины отрезка АВ.
2) Построй 4 прямых угла с общей вершиной в точке О, следуя плану пункта 1, но вместе окружностей проводи дуги (чертёж 2). Любую точку отрезка CD соедини отрезками с точками А и В. Убедись, что полученный треугольник – равнобедренный. Начерти так же ещё 2 равнобедренных треугольника; 1 равносторонний.

1) • Отложи на прямой отрезок АВ = 3 см. • Радиусом больше, чем половина отрезка (в нашем случае больше 1,5 см, например, 2 см) проведи 2 окружности с центрами в точках А и В. • Точки пересечения обозначь буквами C и D. • Проведи через полученные точки прямую, а точку пересечения этой прямой и прямой АВ обозначь буквой D. • Проверь, что все 4 угла с вершиной в точке О.
.jpg)
2) • Треугольник будет равнобедренным, так как его стороны AK и BK являются радиусами равных окружностей, а значит, эти стороны равны. • Чтобы получить равносторонний треугольник, радиус окружностей должен быть равен отрезку AB. • Затем нужно соединить точку пересечения окружностей с точками A и B.
.jpg)
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.