Математика 4 класс учебник Моро, Бантова 1 часть ответы – страница 70

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Странички для любознательных
Номер 1.
Угадай задуманное число.
1) Задумай любое однозначное число, кроме нуля. Умножь его на 9. Результат раздели на задуманное число. Объясни, почему получилось 9. 2) Задумай любое однозначное число, кроме нуля. Увеличь его в 5 раз. Вычти из результата задуманное число. Полученную разность раздели на задуманное число. Прибавь к результату 96. Получилось 100. Объясни, почему всегда получается 100.
Ответ:1) х ∙ 9 : х = 9 2) (х ∙ 5 - х) : х + 96 = 4 ∙ х : х + 96 = 4 + 96 = 100 Мы увеличиваем число в х раз, а потом уменьшаем опять в х раз. Поэтому результат всегда будет 100.
Для того, чтобы объяснить, почему получается, то или иное число, проделай действия, указанные в задании и увидишь закономерность, которая приводит к заранее указанному результату.
Выполним первое задание по алгоритму.
Умножаем это число на 9, т.е. увеличиваем в 9 раз.
Получаем выражение: х · 9
Результат делим на задуманное число, т.е. уменьшаем в х раз.
Получаем выражение: х · 9 : х = 9
Действительно получилось 9, потому что мы умножали и делили на задуманное число из-за этого значение произведения не изменялось.
Выполним второе задание по алгоритму.
Задумываем любое однозначное число – х.
Увеличиваем его в 5 раз, т.е. умножаем на 5. Получаем выражение: х · 5
Вычитаем из результата задуманное число: х · 5 – х = х · 4, потому что умножение – сложение одинаковых слагаемых, значит, вычли один раз по х.
Полученную разность делим на задуманное число: х · 4 : х = 4, потому что делили задуманное число на само себя.
Прибавляем к результату 96: получаем равенство: 96 + 4 = 100
Действительно получилось число 100.
Рассмотрим алгоритм 2 задания и сделаем вывод.
Мы умножаем х на 5, т.е. по х – 5 раз, а затем один раз по х убираем. Значит, теперь осталось всего 4 раза по х. Делим на задуманное число и всегда получаем 4, потому что х : х = 1.
Вывод: таким образом, в обоих случаях неважно, какое число мы задумываем, главное – действия, которые с ним производятся.
Оформляем задание в тетрадь.
1) х ∙ 9 : х = 9
2) (х ∙ 5 – х) : х + 96 = 4 ∙ х : х + 96 = 4 + 96 = 100
Мы увеличиваем число в х раз, а потом уменьшаем опять в х раз.
Поэтому результат всегда будет 100.
Номер 2.
1) Вырежи квадрат со стороной 2 см и разрежь его на 3 таких треугольника, из которых можно составить эти фигуры. 2) Какой будет площадь каждой фигуры?

1)

2) Площадь всех этих фигур равна площадь исходного разрезанного квадрата. Сторона квадрата – 2 см. 2 ∙ 2 = 4 см2
Для того, чтобы понять, как разрезать квадрат на 3 треугольника, чтобы можно было составить все фигуры, начерти эти фигуры на листе в клетку и разбей на треугольники, чтобы они везде получились одинаковыми.
Помни, что площадь сложной фигуры складывается из суммы площадей фигур, из которых она состоит.
Разбиваем фигуры на части.
1)
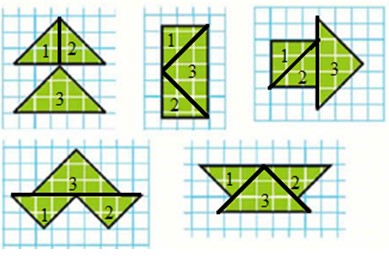
Теперь, когда мы разбили фигуры на части, понятно, на какие треугольники разбивают квадрат со стороной 2 см.
Рассуждаем.
2)Каждая фигура составлена из одних и тех же трех треугольников, которые также составляют вместе квадрат со стороной 2 см. Значит, что площади всех фигур равны площади квадрата. Вычисляем площадь квадрата.
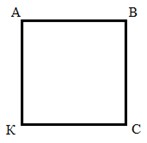
АВСК – квадрат.
АВ = ВС = СК = АК = 2 см.
S = ? см2.
S = АВ · ВС.
S = 2 см · 2 см = 4 см2.
Оформляем задание в тетрадь.
1)

2) Площадь всех этих фигур равна площадь исходного разрезанного квадрата.
Сторона квадрата – 2 см.
2 ∙ 2 = 4 см2
Номер 3.
Расставь знаки арифметических действий и, если нужно, скобки так, чтобы равенства стали верными.
Ответ:(8 ∙ 8 − 8) : 8 = 7
(8 ∙ 8 + 8) : 8 = 9
8 ∙ (8 − 8) + 8 = 8
(8 + 8) : 8 + 8 = 10
Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий. Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Выполняем вычисления.
(8 · 8 – 8) : 8 = 7
1) 8 · 8 = 64
2) 64 – 8 = 64 – (4 + 4) = (64 – 4) – 4 = 60 – 4 = 56, по правилу вычитания суммы из числа.
3) 56 : 8 = 7
(8 · 8 + 8) : 8 = 9
1) 8 · 8 = 64
2) 64 + 8 = 64 + (6 + 2) = (64 + 6) + 2 = 70 + 2 = 72, по правилу прибавления суммы к числу.
3) 72 : 8 = 9
8 · (8 – 8) + 8 = 8
1) 8 – 8 = 0, по правилу вычитания числа из самого себя.
2) 8 · 0 = 0, по правилу умножения числа на 0.
3) 0 + 8 = 8, по правилу прибавления числа к нулю.
(8 + 8) : 8 + 8 = 10
1) 8 + 8 = 8 + (2 + 6) = (8 + 2) + 6 = 10 + 6 = 16, по правилу прибавления суммы к числу.
2) 16 : 8 = 2
3) 2 + 8 = 10
Оформляем задание в тетрадь.
(8 ∙ 8 – 8) : 8 = 7
(8 ∙ 8 + 8) : 8 = 9
8 ∙ (8 – 8) + 8 = 8
(8 + 8) : 8 + 8 = 10
Странички для любознательных
Номер 1.
Угадай задуманное число.
1) Задумай любое однозначное число, кроме нуля. Умножь его на 9. Результат раздели на задуманное число. Объясни, почему получилось 9. 2) Задумай любое однозначное число, кроме нуля. Увеличь его в 5 раз. Вычти из результата задуманное число. Полученную разность раздели на задуманное число. Прибавь к результату 96. Получилось 100. Объясни, почему всегда получается 100.
Ответ:1) х ∙ 9 : х = 9 2) (х ∙ 5 - х) : х + 96 = 4 ∙ х : х + 96 = 4 + 96 = 100 Мы увеличиваем число в х раз, а потом уменьшаем опять в х раз. Поэтому результат всегда будет 100.
Номер 2.
1) Вырежи квадрат со стороной 2 см и разрежь его на 3 таких треугольника, из которых можно составить эти фигуры. 2) Какой будет площадь каждой фигуры? 3) Назови ещё одно свойство, общее для всех фигур на рисунке

1)

2) Площадь всех этих фигур равна площадь исходного разрезанного квадрата. Сторона квадрата – 2 см. 2 ∙ 2 = 4 см2 3) Все эти фигуры – многоугольники.
Номер 3.
Расставь знаки арифметических действий и, если нужно, скобки так, чтобы равенства стали верными.
Ответ:(8 ∙ 8 − 8) : 8 = 7
(8 ∙ 8 + 8) : 8 = 9
8 ∙ (8 − 8) + 8 = 8
(8 + 8) : 8 + 8 = 10
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.