Математика 4 класс учебник Моро, Бантова 1 часть ответы – страница 64

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 291.
Начерти отрезок длиной 60 мм. Узнай, сколько миллиметров в пяти шестых долях этого отрезка.
Ответ:
1) 60 : 6 = 10 (мм) – одна шестая доля этого отрезка.
2) 10 · 5 = 50 (мм).
Ответ: 50 мм в пяти шестых долях этого отрезка.
Доля – одна часть из тех, на которые разделили целое. Например, если целое разделили на 4 части, то доля – это одна четвертая, т.е. одна часть из четырех.
Одна вторая – половина целого.
Одна третья – третья часть от целого.
Одна четвертая – четвертинка или четвертая часть от целого.
Одна пятая – пятая часть от целого и т.д.
Первое слово в названии долей указывает на количество долей, которые взяли, а второе – на сколько частей разделили целое.
Оформляем условие в виде схематического чертежа.
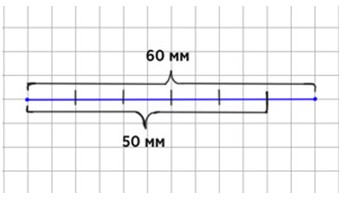
Рассуждаем.
Длина отрезка – 60 мм. Чтобы понять, сколько миллиметров в пяти шестых долях этого отрезка, сначала узнаем, сколько миллиметров составляет одна доля. Для этого, необходимо общую длину отрезка разделить на количество частей.
1) 60 : 6 = 10 (мм) – одна шестая доля этого отрезка.
Продолжаем рассуждение.
Мы узнали, что одну шестую часть составляют 10 мм, а нужно узнать – сколько миллиметров составляют 5 частей. Для этого необходимо длину одной части умножить на количество частей.
2) 10 · 5 = 50 (мм).
Записываем ответ.
Ответ: 50 мм в пяти шестых долях этого отрезка.
Решение выражением:
(60 : 6) · 5, где 60 : 6 – длина одной шестой части отрезка.
Номер 292.
Начерти такой прямоугольник. Вырежи его и разрежь по проведённому в нём отрезку. Проверь наложением, что полученные треугольники равны. Найди площадь одного треугольника.


Площадь прямоугольника: 3 ∙ 5 = 15 см2 = 1500 мм2. Площадь треугольника: 1500 : 2 = 750 мм2.
Фигуры равны, т.е. имеют равную площадь и при наложении совпадают.
Иметь равную площадь не значит быть равным, потому что не всякие равные по площади фигуры совпадут.
Рассуждаем.
Площадь большой фигуры – сумма площадей маленьких фигур, из которых состоит прямоугольник. Чтобы узнать, какова площадь одного треугольника, необходимо сначала вычислить площадь большой фигуры.
Вычисляем площадь треугольника.
Площадь прямоугольника – произведение длин его сторон. Чтобы вычислить площадь прямоугольника, необходимо измерить длины его сторон, а затем полученные значения перемножить.
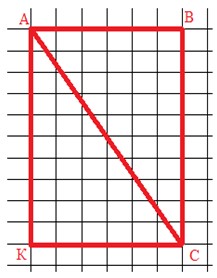
ABCK – прямоугольник.
AB = KC = 3 см.
AK = BC = 5 см.
S = AB · BC.
S = 3 см · 5 см = 15 см2.
Треугольники ACK и ABC равны.
При наложении они совпадут, а их площади равны.
3начит, что сумма двух равных по площади прямоугольников равна площади прямоугольника.
Тогда, чтобы узнать площадь одного из двух прямоугольников, необходимо площадь прямоугольника разделить на 2, ведь треугольника 2.
Тогда, 15 см2 : 2 – разделить нельзя. Вычислю площадь прямоугольника в клетках:
6 кл. · 10 кл. = 60 кл2.
А площадь треугольника:
60 кл2 : 2 = 30 кл2.
Оформляем задание в тетрадь.

Площадь прямоугольника: 3 ∙ 5 = 15 см2 = 1500 мм2.
Площадь треугольника: 1500 : 2 = 750 мм2.
Номер 293.
За 7 дней в столовой израсходовали 21 кг масла. На сколько дней при той же норме расхода хватит 36 кг масла? На сколько дней хватило бы этого масла, если бы каждый день расходовали на 1 кг больше?
Ответ:
1) 21 : 7 = 3 (кг) – масла на 1 день.
2) 36 : 3 = 12 (дн.) – при таком же расходе.
3) 3 + 1 = 4 (кг) – стали расходовать за день.
4) 36 : 4 = 9 (дн.).
Ответ: на 12 дней хватит 36 кг при таком же расходе; на 9 дней при увеличенном расходе.
Помни о том, каков конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а · 3, а – первый множитель, а 3 – количество множителей.
Помни о зависимости между компонентами и результатом действия умножения:
1 множитель · 2 множитель = значение произведения.
Значение произведения : 1 множитель = 2 множитель.
Значение произведения : 2 множитель = 1 множитель.
Данная задача: вида «расход в 1 день, количество дней, общий расход» характеризуется зависимостями между компонентами:
Расход в 1 день · количество дней = общий расход.
Общий расход : количество дней = расход в 1 день.
Общий расход : расход в 1 день = количество дней.
Оформляем условие в виде таблицы.

Рассуждаем.
За 7 дней в столовой израсходовали 21 кг масла. Общее количество масла складывается из количества масла, расходуемого в каждый из дней. Значит, чтобы узнать, каков расход масла в 1 день, необходимо общее количество масла разделить на количество дней.
1) 21 : 7 = 3 (кг) – масла на 1 день.
Продолжаем рассуждение.
Мы узнали, что в 1 день расходуют 3 кг масла. Общее количество масла – 36 кг. Чтобы узнать, на сколько дней хватит 36 кг масла, нужно общее количество масла разделить на расход масла в 1 день.
2) 36 : 3 = 12 (дн.) – при таком же расходе.
Продолжаем рассуждение.
Расход масла в 1 день – 3 кг. Расходовали каждый день на 1 кг больше. Получается, чтобы узнать, сколько молока расходовали в каждый день, нужно к данному расходу прибавить 1 кг.
3) 3 + 1 = 4 (кг) – стали расходовать за день.
Продолжаем рассуждение.
Увеличенный расход масла в день – 4 кг, а общее количество масла – 36 кг. Неизвестно только количество дней. При этом, из таблицы видно, что общее количество масла складывается из количества масла, расходуемого в каждый из дней. Значит, чтобы узнать, на сколько дней хватит 36 кг масла, нужно общее количество масла разделить на расход масла в 1 день.
4) 36 : 4 = 9 (дн.).
Записываем ответ.
Ответ: на 12 дней хватит 36 кг при таком же расходе;
на 9 дней при увеличенном расходе.
Номер 294.
Ответ:

Помни о том, что существует алгоритм письменного деления. Следуй ему, объясняя, как выполняешь деление:
1) Выделю первое неполное делимое, чтобы определить количество цифр в частном.
2) Нахожу цифру сотен в частном:
3) Нахожу, сколько сотен разделили:
4) Нахожу, сколько сотен осталось разделить:
5) Образую второе неполное делимое:
6) Нахожу, количество десятков в частном:
7) Нахожу, сколько десятков разделили:
8) Нахожу, сколько десятков осталось разделить:
9) Образую третье неполное делимое:
10) Нахожу количество единиц в частном:
11) Нахожу, сколько единиц разделили:
12) Нахожу, сколько единиц осталось разделить:
13) Читаю ответ.
Помни о том, что существует алгоритм объяснения умножения трехзначного числа на однозначное. Следуй ему:
1) Записываю первый множитель так, чтобы каждая цифра стояла в своей клетке. Ставлю знак умножить;
2) Записываю второй множитель так, чтобы разряд стоял под разрядом;
3) Провожу черту, обозначающую знак равно;
4) Умножение начинаю с единиц низшего разряда;
5) Умножаю десятки;
6) Умножаю сотни;
7) Умножение окончено. Читаю ответ.
Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий. Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Выполняем умножение.
231 · 4 (аналогично 304 · 3, 129 · 6)
1) Записываю первый множитель так, чтобы каждая цифра стояла в своей клетке. Ставлю знак умножить;
2) Записываю второй множитель так, чтобы разряд стоял под разрядом;
3) Провожу черту, обозначающую знак равно;
4) Умножение начинаю с единиц низшего разряда; 1 ед. · 4 = 4 ед. 4 ед. < 10 ед., значит, в разряд единиц записываю 4 единицы.
5) Умножаю десятки; 3 дес. · 4 = 12 дес. – это 1 сот. 2 дес., значит, 2 десятка записываю в разряд десятков, а 1 сот. запоминаю.
6) Умножаю сотни; 2 сот. · 4 = 8 сот. да еще 1 сот. – 9 сот. 9 сот меньше, чем 10 сот, значит, 9 сотен записываю в разряд сотен.
7) Умножение окончено. Читаю ответ. Значение произведения от умножения 231 на 4 равно 924.
Выполняем деление.
984 : 8 (аналогично 938 : 7, 876 : 4)
1) Выделю первое неполное делимое, чтобы определить количество цифр в частном. Первое неполное делимое – 9 сот. Высший разряд – сотни, значит, в частном 3 знака.
2) Нахожу цифру сотен в частном: 9 сот. : 8 = 1 сот.
3) Нахожу, сколько сотен разделили: 1 сот. · 8 = 8 сот.
4) Нахожу, сколько сотен осталось разделить: 9 сот. – 8 сот. = 1 сот., 1 сотня меньше, чем 8, значит, в значении частном 1 сотня.
5) Образую второе неполное делимое: 1 сот. – 10 дес. да еще 8 дес. – 18 дес.
6) Нахожу, количество десятков в частном: 18 дес. : 8 = 2 дес.
7) Нахожу, сколько десятков разделили: 2 дес. · 8 = 16 дес.
8) Нахожу, сколько десятков осталось разделить: 18 дес. – 16 дес. = 2 дес., 2 десятка меньше, чем 8, значит, в значении частного 2 десятка.
9) Образую третье неполное делимое: 2 десятка – это 20 единиц да еще 4 единицы – 24 единицы.
10) Нахожу количество единиц в частном: 24 ед. : 8 = 3 ед.
11) Нахожу, сколько единиц разделили: 3 ед. · 8 = 24 ед.
12) Нахожу, сколько единиц осталось разделить: 24 ед. – 24 ед. = 0 ед. 0 единиц меньше, чем 8, значит, в значении частного 3 единицы.
13) Читаю ответ. Значение частного от деления 984 на 8 равно 123.
Оформляем задание в тетрадь.


Номер 295.
Сравни уравнения каждой пары и их решения.
Ответ:
Уравнение – равенство с неизвестной, при подстановке числа в которую, получается верное равенство.
Вспомни названия компонентов действия умножения, и зависимость между компонентами и результатом действия умножения:
1 множитель · 2множитель = значение произведения.
Значение произведения : 1 множитель = 2 множитель.
Значение произведения : 2 множитель = 1 множитель.
Уменьшаемое – вычитаемое = значение разности.
Уменьшаемое – значение разности = вычитаемое.
Значение разности + вычитаемое = уменьшаемое.
Делимое : делитель = значение разности.
Делимое : значение разности = делитель.
Значение разности · делитель = делимое.
Решаем уравнения и сравниваем первую пару.
х + 75 = 125 · 3
х + 75 = 375
х = 375 – 75
х = 300
х - 75 = 125 · 3
х - 75 = 375
х = 375 + 75
х = 450
Уравнения похожи тем, что перед поиском неизвестного компонента нужно найти значения произведения в правой части после знака равно. В уравнениях использованы одинаковые числа, но действия над ними производятся различные. В первом уравнении неизвестное слагаемое находится вычитанием. Во втором – неизвестное уменьшаемое находится сложением.
Решаем уравнения и сравниваем вторую пару.
х · 10 = 250
х = 250 : 10
х = 25
х : 10 = 250
х = 250 · 10
х = 2500
В уравнениях использованы одинаковые числа, но действия над ними производятся различные. В первом уравнении неизвестный множитель находится делением. Во втором – неизвестное делимое находится умножением.
Решаем уравнения и сравниваем третью пару.
х : 7 = 140
х = 140 · 7
х = 980
140 : х = 7
х = 140 : 7
х = 20
В уравнениях использованы одинаковые числа, но они стоят на других местах, и действия над ними производятся различные. В первом уравнении неизвестное делимое находится умножением. Во втором – неизвестный делитель находится делением.
Решаем уравнения и сравниваем четвертую пару.
32 : х = 32
х = 32 : 32
х = 1
32 · х = 32
х = 32 : 32
х = 1
В уравнениях использованы одинаковые числа, но действия над ними производятся различные. Несмотря на это, поиск неизвестного компонента находится одинаковым действием, ответ тоже одинаковый.
Оформляем задание в тетрадь.
Задание внизу страницы.
На сколько равных частей разделён каждый квадрат на чертеже? Найди площадь одной доли в каждом квадрате. Сравни площади этих долей.

Квадраты разделены на 4 части.
Площадь квадратов: 2 ∙ 2 = 4 см2.
Площадь одной доли квадратов: 4 : 4 = 1 см2.
Площади долей равны, ведь они делят квадрат на 4 части и при этом общая площадь квадрата не меняется.
Доля – одна часть из тех, на которые разделили целое. Например, если целое разделили на 4 части, то доля – это одна четвертая, т.е. одна часть из четырех.
Одна вторая – половина целого.
Одна третья – третья часть от целого.
Одна четвертая – четвертинка или четвертая часть от целого.
Одна пятая – пятая часть от целого и т.д.
Первое слово в названии долей указывает на количество долей, которые взяли, а второе – на сколько частей разделили целое.
Рассуждаем.

При сравнении квадратов на глаз они кажутся равными, т.е. площади равны, при наложении совпадут. Но это лишь предположение, поэтому вычислим площади фигур. Это квадраты, поэтому площадь фигуры – произведение стороны и стороны.
Значит, а · а, где а = 2 см. Тогда, S = 2 см · 2 см = 4 см2.
В каждой фигуре 4 доли, а доля – значит равная часть. Поэтому, чтобы вычислить площадь доли, нужно площадь фигуры разделить на количество долей.
Тогда, 4 см2 : 4 = 1 см2.
Значит, площади долей равны.
Оформляем задание в тетрадь.
Квадраты разделены на 4 части.
Площадь квадратов: 2 ∙ 2 = 4 см2.
Площадь одной доли квадратов: 4 : 4 = 1 см2.
Площади долей равны, ведь они делят квадрат на 4 части и при этом общая площадь квадрата не меняется.
Задание на полях страницы.
Ребус.


Вспомни названия компонентов действия деления и зависимости между компонентами и результатом действия деления:
делимое: делитель = значение частного.
делимое : значение частного = делитель.
значение частного · делитель = делимое.
Рассуждаем.
Данный ребус основан на арифметическом действии деления. В значении частного 2 знака, значит, было 2 неполных делимых.
Первое неполное делимое неизвестно, но результат умножения количество десятков на делитель равно 36, да еще остаток 6, значит, первое неполное делимое: 36 + 6 = 42.
Количество десятков в значении частного: 36 : 9 = 4 дес.
Второе неполное делимое, оно же последнее, делится без остатка на 9. При этом, количество десятков равно 6. Вспомню по таблице умножения 9, в каком числе 6 десятков. Это число 63, значит, 63 ед. : 9 = 7 ед. Значит, количество единиц в делимом – 3, а количество единиц в значении частного – 7 ед.
Получаем равенство: 423 : 9 = 47.
Оформляем задание в тетрадь.

Номер 295.
Начерти отрезок длиной 60 мм. Узнай, сколько миллиметров в пяти шестых долях этого отрезка.
Ответ:
1) 60 : 6 = 10 (мм) – одна шестая доля этого отрезка.
2) 10 · 5 = 50 (мм).
Ответ: 50 мм в пяти шестых долях этого отрезка.
Номер 296.
Начерти такой прямоугольник. Вырежи его и разрежь по проведённому в нём отрезку. Проверь наложением, что полученные треугольники равны. Найди площадь одного треугольника.


Площадь прямоугольника: 3 ∙ 5 = 15 см2 = 1500 мм2. Площадь треугольника: 1500 : 2 = 750 мм2.
Номер 297.
За 7 дней в столовой израсходовали 21 кг масла. На сколько дней при той же норме расхода хватит 36 кг масла? На сколько дней хватило бы этого масла, если бы каждый день расходовали на 1 кг больше?
Ответ:
1) 21 : 7 = 3 (кг) – масла на 1 день.
2) 36 : 3 = 12 (дн.) – при таком же расходе.
3) 3 + 1 = 4 (кг) – стали расходовать за день.
4) 36 : 4 = 9 (дн.)
Ответ: на 12 дней хватит 36 кг при таком же расходе; на 9 дней при увеличенном расходе.
Номер 298.
Ответ:

Номер 299.
Чем похожи и чем различаются уравнения и их решения в каждой паре?
x + 75 = 125 · 3
x – 75 = 125 · 3
x · 10 = 250
x : 10 = 250
x : 7 = 140
140 : x = 7
32 : x = 32
32 · x = 32

Задание внизу страницы.
На сколько равных частей разделён каждый квадрат на чертеже? Найди площадь одной доли в каждом квадрате. Сравни площади этих долей.

Квадраты разделены на 4 части.
Площадь квадратов: 2 ∙ 2 = 4 см2.
Площадь одной доли квадратов: 4 : 4 = 1 см2.
Площади долей равны, ведь они делят квадрат на 4 части и при этом общая площадь квадрата не меняется.
Задание на полях страницы.
Ребус.


С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.