Математика 4 класс учебник Моро, Бантова 1 часть ответы – страница 63

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 283.
Прочитай на странице 105, как связаны между собой числа при вычитании, и заполни таблицу.
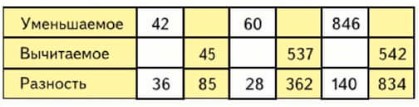
- Объясни решение уравнений и их проверку.
Если к разности прибавить вычитаемое, то получится уменьшаемое. Если из уменьшаемого вычесть разность, то получится вычитаемое.


Сразу мы не можем решить эти уравнения, потому что не знаем результат разностей. Поэтому сначала нужно посчитать правую часть после знака равно, то есть найти результат разностей. Затем уравнения решаются как обычно через нахождение неизвестных уменьшаемого и вычитаемого.
Вспомни названия компонентов действия вычитания и зависимость между компонентами и результатом действия вычитания:
Уменьшаемое – вычитаемое = значение разности.
Уменьшаемое – значение разности = вычитаемое.
Значение разности + вычитаемое = уменьшаемое.
Рассуждаем и выполняем вычисления.
Если к разности прибавить вычитаемое, то получится уменьшаемое. Если из уменьшаемого вычесть разность, то получится вычитаемое.
42 – 36 = 42 – (32 + 4) = (42 – 32) – 4 = 10 – 4 = 6, по правилу вычитания суммы из числа.
85 + 45 = 85 + (40 + 5) = (85 + 5) + 40 = 90 + 40 = 130, по правилу прибавления суммы к числу.
60 – 28 = 60 – (20 + 8) = (60 – 20) – 8 = 40 – 8 = 32, по правилу вычитания суммы из числа.
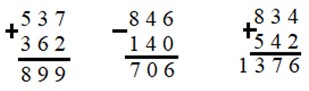
Заполняем таблицу.

Объясняем решение уравнений.
Сразу мы не можем решить эти уравнения, потому что не знаем результат разностей. Поэтому сначала нужно посчитать правую часть после знака равно, то есть найти результат разностей. Затем уравнения решаются как обычно через нахождение неизвестных уменьшаемого и вычитаемого.

Номер 284.
Реши уравнения.
Ответ:
Уравнение – равенство с неизвестной, при подстановке числа в которую, получается верное равенство.
Вспомни названия компонентов действия умножения, и зависимость между компонентами и результатом действия умножения:
1 множитель · 2 множитель = значение произведения.
Значение произведения : 1 множитель = 2 множитель.
Значение произведения : 2 множитель = 1 множитель.
Уменьшаемое – вычитаемое = значение разности.
Уменьшаемое – значение разности = вычитаемое.
Значение разности + вычитаемое = уменьшаемое.
Делимое : делитель = значение разности.
Делимое : значение разности = делитель.
Значение разности · делитель = делимое .
Рассуждаем и выполняем вычисления первого уравнения.
Преобразую правую часть уравнения, вычисляя значение частного.
64 - x = 91 : 7
Данное уравнение основано на арифметическом действии вычитания. х - неизвестное вычитаемое. Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть значение разности.
64 - x = 13
x = 64 – 13
x = 51
Проверяю правильность вычислений. Для этого подставляю значение х в уравнение и вычисляю.
64 - 51 = 91 : 7
13 = 13
Значения совпали, значит, уравнение решено верно. Записываю ответ.
Ответ: x = 13
Рассуждаем и выполняем вычисления второго уравнения.
Преобразую правую часть уравнения, вычисляя значение частного.
x – 85 = 350 + 150
Данное уравнение основано на арифметическом действии вычитания. х – неизвестное уменьшаемое. Чтобы найти неизвестное уменьшаемое, нужно к значению разности прибавить вычитаемое.
x – 85 = 500
x = 500 + 85
x = 585
Проверяю правильность вычислений. Для этого подставляю значение х в уравнение и вычисляю.
585 – 85 = 350 + 150
500 = 500
Значения совпали, значит, уравнение решено верно. Записываю ответ.
Ответ: x = 500
Делаем вывод.

Номер 285.
Вычисли и сделай проверку.
Ответ:
Помни о названии компонентов действия сложения и зависимости между компонентами и результатом действия:
1 слагаемое + 2 слагаемое = значение суммы.
Значение суммы – 1 слагаемое = 2 слагаемое.
Значение суммы – 2 слагаемое = 1 слагаемое.
Помни о том, что существует алгоритм письменного сложения.
Помни о том, что существует алгоритм письменного сложения и вычитания. Многозначные числа необходимо записывать предельно внимательно, чтобы каждый разряд стоял под разрядом. Следуй алгоритму письменного сложения и вычитания:
Сложение:
1) Записываю первое слагаемое так, чтобы каждый знак стоял в отдельной клетке, ставлю знак плюс.
2) Записываю второе слагаемое так, чтобы каждый разряд стоял под своим разрядом;
3) Провожу черту, обозначающую знак равно;
4) Сложение начинаю с единиц низшего разряда. Складываю единицы.
5) Складываю десятки (и так до максимального разряда).
6) Сложение окончено. Читаю ответ. Значение суммы от сложения ...
Вычитание:
1) Записываю уменьшаемое так, чтобы каждая цифра стояла в своей клетке, ставлю знак минус.
2) Записываю вычитаемое так, чтобы разряд стоял под разрядом.
3) Провожу черту, обозначающую знак равно.
4) Вычитание начинаю с единиц низшего разряда.
5) Вычитаю десятки (и так до максимального разряда).
6) Вычитание окончено. Читаю ответ. Значение разности от вычитания ...
Выполняем вычисления с проверкой.
Пишу (единицы под единицами, десятки под десятками, сотни под сотнями, единицы тысяч под единицами тысяч, десятки тысяч под десятками тысяч, сотни тысяч под сотнями тысяч):
324 544 + 175 737.
Складываю единицы: 7 + 4 = 11. 11 ед. – это 1 дес. и 1 ед.; 1 ед. пишу под единицами, а 1 дес. прибавлю к десяткам.
Складываю десятки: 4 + 3 = 7, да ещё 1.
7 + 1 = 8.
8 дес. пишу под десятками.
Складываю сотни: 5 + 7 = 12. 12 сот. – это 1 ед. тыс. и 2 сот., 2 сот. пишу под сотнями, а 1 ед. тыс. прибавлю к ед. тысяч.
Складываю единицы тысяч: 4 + 5 = 9, да ещё 1.
9 + 1 = 10. 10 единиц тысяч – это 1 дес. тыс. и 0 ед. тыс.; 0 ед. тыс. пишу под единицами тысяч, а 1 дес. тыс. прибавлю к десяткам тысяч.
Складываю десятки тысяч: 2 + 7 = 9, да ещё 1.
9 + 1 = 10. 10 дес. тыс. – это 1 сот. тыс. и 0 дес. тыс.; пишу 0 под десятками тысяч, а 1 сот. тыс. прибавлю к сотнями тысяч.
Складываю сотни тысяч: 3 + 1 = 4, да ещё 1.
4 + 1 = 5. Пишу 5 под сотнями тысяч.
Читаю ответ: 500 281.
Пишу (единицы под единицами, десятки под десятками, сотни под сотнями, единицы тысяч под единицами тысяч, десятки тысяч под десятками тысяч):
840 103 – 62 524.
Вычитаю единицы: из 3 ед. нельзя вычесть 4 ед. Взять 1 дес. из 0 нельзя, поэтому возьму 1 сот. из 1 сот. (Чтобы не забыть об этом, ставлю точку над цифрой 1.) 1 сот. – это 10 дес. Беру 1 дес. из 10 дес. (Чтобы не забыть об этом, ставлю точку над цифрой 0). 1 дес. и 3 ед. – это 13 ед. Из 13 вычесть 4, получится 9. Пишу 9 под единицами.
Вычитаю десятки: было 10 дес., но 1 взяли при вычитании единиц, осталось 9 дес. Из 9 вычесть 2, получится 7. Пишу 7 под десятками.
Вычитаю сотни: была 1 сот., но её взяли при вычитании единиц. Из 0 сот. нельзя вычесть 5 сот. Из 0 ед. тыс. нельзя вычесть 1 ед. тыс., поэтому возьму 1 дес. тыс. из 4 дес. тыс. (Чтобы не забыть об этом, ставлю точек над цифрой 4). 1 дес. тыс. – это 10 сот. Из 10 вычесть 5, получится 5. Пишу 5 под сотнями.
Вычитаю единицы тысяч: было 10 ед. тыс., но 1 ед. тыс. взяли при вычитании сотен, осталось 9 ед. тыс. Из 9 вычесть 2, получится 7. Пишу 7 под единицами тысяч.
Вычитаю десятки тысяч: было 4 дес. тыс., но 1 дес. тыс. взяли при вычитании сотен, осталась 3 дес. тыс. Из 3 дес. тыс. нельзя вычесть 6 дес. тыс. Беру 1 сот. тыс. из 8 сот. тыс. (Чтобы не забыть об этом, ставлю точку над цифрой 8). 1 сот. тыс. и 3 дес. тыс. – это 13 дес. тыс. Из 13 вычесть 6, получится 7. Пишу 7 под десятками тысяч.
Вычитаю сотни тысяч: было 8 сот. тыс., но 1 сот. тыс. взяли при вычитании дес. тыс., осталось 7 сот. тыс. Пишу 7 под сот. тыс., так как разряд сотен тысяч в вычитаемом отсутствует.
Читаю ответ: 777 579.
Оформляем задание в тетрадь.

Номер 286.
В магазин привезли хлеб. За день было продано 176 кг хлеба, после чего в магазине осталось на 145 кг хлеба меньше, чем продали. Сколько килограммов хлеба привезли?
Ответ:
1) 176 – 145 = 31 (кг) – хлеба осталось.
2) 176 + 31 = 207 (кг)
Ответ: 207 кг хлеба привезли.
«на 145 кг больше», значит, вычисляется сложением.
«всего», значит, вычисляется сложением.
Оформляем условие в виде краткой записи.

Рассуждаем.
За день продали 176 кг хлеба, а осталось на 145 кг хлеба меньше. На 145 кг меньше, значит, что осталось столько хлеба, сколько продали, но без 176 кг хлеба. Получается, чтобы узнать, сколько кг хлеба осталось, нужно из количества проданного хлеба вычесть 145 кг хлеба.
1) 176 – 145 = 31 (кг) – хлеба осталось.
Продолжаем рассуждение.
Общее количество хлеба складывается из количества проданного хлеба и оставшегося. Значит, чтобы узнать, сколько всего хлеба привезли, складываю количество проданного хлеба и оставшегося.
2) 176 + 31 = 207 (кг).
Записываем ответ.
Ответ: 207 кг хлеба привезли.
Решение выражением: 176 + (176 – 145), где 176 – 145 – количество оставшегося хлеба.
Номер 287.
В зале 300 мест. Когда школьники заняли 8 полных рядов, в зале осталось 140 свободных мест. Сколько мест в каждом ряду, если все ряды одинаковые?
Ответ:Всего – 300 м.
Заняли – 8 р. по ? м.
Осталось – 140 м.
1) 300 – 140 = 160 (м.) – занято школьниками.
2) 160 : 8 = 20 (м.).
Ответ: 20 мест в одном ряду.
Помни о том, каков конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а · 3, а – первый множитель, а 3 – количество множителей.
Помни о зависимости между компонентами и результатом действия умножения:
1 множитель · 2 множитель = значение произведения.
Значение произведения : 1 множитель = 2 множитель.
Значение произведения : 2 множитель = 1 множитель.
Данная задача: вида «кол-во мест в ряду, кол-во рядов, общее кол-во мест» характеризуется зависимостями между компонентами:
Кол-во мест в 1 ряду · кол-во мест = общее кол-во мест.
Общее кол-во мест : кол-во мест в 1 ряду = кол-во мест.
Общее кол-во мест : кол-во мест = кол-во мест в 1 ряду.
Оформляем условие в виде краткой записи.
Всего – 300 м.
Заняли – 8 р. по ? м.
Осталось – 140 м.
Рассуждаем.
Общее количество мест складывается из количества занятых мест и оставшихся. Значит, чтобы узнать, сколько мест занято, нужно из общего количества мест вычесть количество оставшихся.
1) 300 – 140 = 160 (м.) – занято школьниками.
Продолжаем рассуждение.
Чтобы узнать, сколько стульев в 1 ряду, нужно общее количество стульев разделить на количество рядов.
2) 160 : 8 = 20 (м.).
Записываем ответ.
Ответ: 20 мест в одном ряду.
Решение выражением: (300 – 140) : 8, где 300 – 140 – количество занятых мест.
Номер 288.
Чему равна третья часть отрезка длиной 48 мм?
Ответ:48 : 3 = 16 (мм) – третья часть отрезка.
Ответ: длина третьей части отрезка составляет 16 мм.
Вид задачи: на нахождение части по целому.
Модель: схематический чертеж.
Фигура симметрична относительно прямой, если для каждой точки фигуры есть симметричная ей точка, которая принадлежит этой фигуре.
Оформляем условие в виде схематического чертежа.
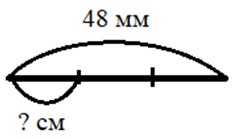
Рассуждаем.
Длина всей часть – 48 мм. Третья часть, т.е. одна из трех. Получается, нужно длину всего отрезка разделить на 3, а взять только одну.
48 : 3 = 16 (мм) – третья часть отрезка.
Записываем ответ.
Ответ: 16 мм.
Номер 289.
Вырази:
1) в миллиметрах: 9 см, 80 см, 2 м 25 см; 2) в минутах: 9 ч, 180 с, 2 ч 25 мин.
Ответ:1) 9 см = 90 мм; 80 см = 800 мм; 2 м 25 см = 2250 мм. 2) 9 ч = 540 мин; 180 с = 3 мин; 2 ч 25 мин = 145 мин.
Длина – величина, характеризующая протяженность объекта на плоскости, выражается в таких единицах измерения, как миллиметр, сантиметр, дециметр, метр, километр.
Помни о соотношении числовых значений единиц измерения длины:
1 см = 10 мм.
1 дм = 10 см.
1 м = 100 см.
1 м = 10 дм.
1 км = 1000 м.
Время – величина, характеризующая продолжительность какого-либо события и отношения его к временной прямой: прошлому, настоящему или будущему. Измеряется в таких единицах измерения, как: 1 секунда, 1 минута, 1 час, 1 сутки, 1 неделя, 1 месяц, 1 год, 1 век.
Помни о соотношении числовых значений единиц измерения времени:
1 мин – 60 сек.
1 час – 60 мин.
1 сут – 24 час.
1 мес – 28, 29, 30 или 31 сут.
1 год – 12 мес.
1 год – 356 сут.
Выразим в миллиметрах данные значения.
9 см; 1 см – 10 мм, значит, 10 мм · 9 = 90 мм.
80 см; 1 см – 10 мм, значит, 10 мм · 80 = 800 мм.
2 м 25 см; 1 м – 100 см, а 1 см – 10 мм, значит, 1 м – 1000 мм. Тогда, 2 м – 1000 мм и 25 см – 250 мм. Тогда, 2000 мм + 250 мм = 2250 мм.
Выразим в минутах данные значения.
9 ч; 1 ч – 60 мин, а 60 мин · 9 = 540 мин.
180 с; 1 мин – 60 сек, значит, 180 с : 60 = 3 мин.
2 ч 25 мин; 1 ч – 60 мин, значит, 60 мин · 2 = 120 мин да еще 25 мин – 145 мин.
Оформляем задание в тетрадь.
1) 9 см = 90 мм;
80 см = 800 мм;
2 м 25 см = 2250 мм.
2) 9 ч = 540 мин;
180 с = 3 мин;
2 ч 25 мин = 145 мин.
Номер 290.
Ответ:
Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий. Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
Сложение:
1) Записываю первое слагаемое так, чтобы каждый знак стоял в отдельной клетке, ставлю знак плюс.
2) Записываю второе слагаемое так, чтобы каждый разряд стоял под своим разрядом;
3) Провожу черту, обозначающую знак равно;
4) Сложение начинаю с единиц низшего разряда. Складываю единицы.
5) Складываю десятки (и так до максимального разряда).
6) Сложение окончено. Читаю ответ. Значение суммы от сложения ...
Вычитание:
1) Записываю уменьшаемое так, чтобы каждая цифра стояла в своей клетке, ставлю знак минус.
2) Записываю вычитаемое так, чтобы разряд стоял под разрядом.
3) Провожу черту, обозначающую знак равно.
4) Вычитание начинаю с единиц низшего разряда.
5) Вычитаю десятки (и так до максимального разряда).
6) Вычитание окончено. Читаю ответ. Значение разности от вычитания ...
Выполняем вычисления по действиям.
60 005 + (36 006 – 28 097) = 67 914

100 105 – (87 007 – 679) = 13 777
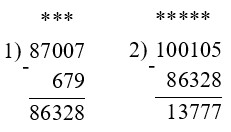
400 + 80 : 4 · 5 = 500
1) 80 : 4 = 20
2) 20 · 5 = 100
3) 400 + 100 = 500
800 – 640 : 2 : 4 = 720
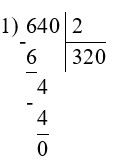
2) 320 : 4 = 80
3) 800 – 80 = 720
Оформляем задание в тетрадь.

Задание внизу страницы.
Начерти отрезок, пятая часть которого равна 17 мм.
Ответ:17 ∙ 5 = 85 85 мм = 8 см 5 мм. Чертим отрезок длиной 8 см 5 мм.

Вид задачи: на нахождение целого по части.
Модель: схематический чертеж.
Оформляем условие в виде схематического чертежа.
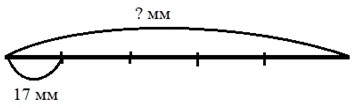
Рассуждаем.
17 мм – длина пятой части отрезка. Пятая часть, т.е. одна из пяти. Значит, чтобы узнать, чему равна длина всего отрезка, нужно длину одной части умножить на их количество.
17 ∙ 5 = 85
85 мм = 8 см 5 мм.
Чертим отрезок длиной 8 см 5 мм.

Записываем ответ.
Ответ: длина отрезка – 85 мм.
Задание на полях страницы.
△? ◯?
380 – △ = ◯ ◯ – 120 = 40
Ответ:△ = 220 ◯ = 160 380 – 220 = 160 160 – 120 = 40
Начни решение задачи с того равенства, где вычислить число, прячущееся за фигурой проще. Это равенство 2. Начни с него.
Рассуждаем и выполняем вычисления.
380 – △ = ◯
◯ – 120 = 40
Начинаем со втоpого pавенства, потому что в нем вычислить значение фигуры прoще.
Даное равенство основано на арифметическом действии вычитания.
Зеленый круг – неизвестное уменьшаемое. Чтобы найти неизвестное уменьшаемое, нужно к значенио разности прибавить вычитаемoe.
Тогда, зеленый крут = 40 + 120 = 160.
Подставляю число зеленого круга в первое равенство.
Получаю: 380 – голубой треутольник = 160.
Данное равенство основано на арифметическом действии вычитания.
Голубой треугольник – неизвестное вычитаемое. Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть значение разиости.
Тогда, голубой треутольник = 380 – 160 = 220.
Выполняем проверку.
Подставляю полученные значения для того, чтобы проверить правильность выполнения действий:
380 – 160 = 220
160 – 120 = 40
Оформляем задание в тетрадь.
△ = 220
◯ = 160
380 – 220 = 160
160 – 120 = 40
Номер 287.
Прочитай на странице 103, как связаны между собой числа при вычитании, и заполни таблицу.

- Объясни решение уравнений и их проверку.
Если к разности прибавить вычитаемое, то получится уменьшаемое. Если из уменьшаемого вычесть разность, то получится вычитаемое.


Сразу мы не можем решить эти уравнения, потому что не знаем результат разностей. Поэтому сначала нужно посчитать правую часть после знака равно, то есть найти результат разностей. Затем уравнения решаются как обычно через нахождение неизвестных уменьшаемого и вычитаемого.
Номер 288.
Реши уравнения.
Ответ:
Номер 289.
Вычисли и сделай проверку.
Ответ:
Номер 290.
На полке магазина лежат пакеты с яблоками разной массы: 1 кг 200 г, 2 кг 100 г, 1 кг 900 г, 1 кг 700 г. Какие 2 пакета с яблоками надо взять, чтобы их масса была меньше трёх килограммов?
Ответ:1 кг 200 г + 1 кг 700 г = 2 кг 900 г. Нужно взять пакеты с массой 1 кг 200 г и 1 кг 700 г.
Номер 291.
В зале 300 мест. Когда школьники заняли 8 полных рядов, в зале осталось 140 свободных мест. Сколько мест в каждом ряду, если все ряды одинаковые?
Ответ:Всего – 300 м.
Заняли – 8 р. по ? м.
Осталось – 140 м.
1) 300 – 140 = 160 (м.) – занято школьниками.
2) 160 : 8 = 20 (м.)
Ответ: 20 мест занято всего в каждом ряду.
Номер 292.
1) Чему равна третья часть отрезка длиной 48 мм? 2) Начерти отрезок АВ. Начерти симметричный ему отрезок.

1) 48 : 3 = 16 (мм) — третья часть отрезка.
Ответ: третья часть длины отрезка составляет 16 мм.
2) отрезок А1В1 симметричен отрезку АВ.

Номер 293.
Вырази:
1) в миллиметрах: 9 см, 80 см, 2 м 25 см; 2) в минутах: 9 ч, 180 с, 2 ч 25 мин.
Ответ:1) 9 см = 90 мм; 80 см = 800 мм; 2 м 25 см = 2250 мм. 2) 9 ч = 540 мин; 180 с = 3 мин; 2 ч 25 мин = 145 мин.
Номер 294.
Ответ:
Задание внизу страницы.
Начерти отрезок, пятая часть которого равна 17 мм.
Ответ:17 ∙ 5 = 85 85 мм = 8 см 5 мм. Чертим отрезок длиной 8 см 5 мм.

Задание на полях страницы.
△? ◯?
380 – △ = ◯ ◯ – 120 = 40
Ответ:△ = 220 ◯ = 160 380 – 220 = 160 160 – 120 = 40
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.