Математика 4 класс учебник Моро, Бантова 1 часть ответы – страница 61

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Задание вверху страницы.
Объясни вычисления.


Вычитаем единицы. От нуля отнять 6 мы не можем. Занимаем у десятков. В разряде десятков отсутствуют единицы. Занимаем у сотен. Одна сотня – это десять десятков. Теперь один десяток мы можем отдать.
10 – 6 = 4. Записываем под единицами.
Вычитаем десятки. Мы добавили к десяткам одну сотню, то есть десять десятков, но при этом заняли десяток, осталось 9 дес. 9 – 2 = 7 Записываем под десятками.
Вычитаем сотни. Мы заняли одну сотню из шести, поэтому записываем пять сотен.
Читаем ответ: 574.

Вычитаем единицы. Из нуля вычесть четыре нельзя, потому занимаем один десяток. Но единицы в разряде десятков отсутствуют, потому занимаем сотню. Единицы в разряде сотен отсутствуют, потому занимаем тысячу.
Одина тысяча – это десять сотен, можем занять одну сотню. Одна сотня – это десять десятков, теперь занимаем один десяток. Один десяток – это десять единиц. 10 – 4 = 6.
Вычисляем десятки. Мы добавили 10 десятков, но один заняли. 9 – 2 = 7 десятков.
Вычисляем сотни. Мы добавили 10 сотен, но одну заняли, осталось 9. 9 – 1 = 8 сотен.
Вычисляем единицы тысяч. Была 1 тысяча, но ее мы заняли. Осталось ноль, но его мы не пишем.
Читаем ответ: 876.

Вычитаем единицы. Из семи вычесть восемь нельзя, потому занимаем один десяток. Но единицы в разряде десятков отсутствуют, потому занимаем сотню. Отсутствуют сотни и отсутствуют единицы тысяч, потому занимаем один десяток тысяч.
Один десяток тысяч — это десять единиц тысяч, можем занять одну тысячу. Одна тысяча – это 10 сотен, можем занять из сотен. Одна сотня – это десять десятков, теперь занимаем один десяток. Один десяток – это десять единиц да ещё 7. 17 – 8 = 9.
Вычисляем десятки. Мы добавили 10 десятков, но один заняли. 9 – 4 = 5 десятков.
Вычисляем сотни. Мы добавили 10 сотен, но одну заняли, осталось 9. 9 – 6 = 3 сотни.
Вычисляем единицы тысяч. Мы добавили 10 единиц тысяч, но одну заняли, осталось 9 единиц тысяч. Переписываем 9, так как единицы тысяч в вычитаемом отсутствуют.
Осталось два десятка тысяч, их переписываем.
Читаем ответ: 29 359.
Помни о том, что существует алгоритм письменного вычитания. Многозначные числа необходимо записывать предельно внимательно, чтобы каждый разряд стоял под разрядом. Следуй алгоритму письменного вычитания:
1) Записываю уменьшаемое так, чтобы каждая цифра стояла в своей клетке, ставлю знак минус.
2) Записываю вычитаемое так, чтобы разряд стоял под разрядом.
3) Провожу черту, обозначающую знак равно.
4) Вычитание начинаю с единиц низшего разряда.
5) Вычитаю десятки ( и так до максимального разряда).
6) Вычитание окончено. Читаю ответ. Значение разности от вычитания.
Объясняем вычисление первого примера.

1) Вычитаем единицы. От нуля отнять 6 мы не можем. Занимаем у десятков. В разряде десятков отсутствуют единицы. Занимаем у сотен. Одна сотня – это десять десятков. Теперь один десяток мы можем отдать.
10 – 6 = 4. Записываем под единицами.
2) Вычитаем десятки. Мы добавили к десяткам одну сотню, то есть десять десятков, но при этом заняли десяток, осталось 9 дес. 9 – 2 = 7 Записываем под десятками.
3) Вычитаем сотни. Мы заняли одну сотню из шести, поэтому записываем пять сотен.
4) Читаем ответ: 574.
Объясняем вычисление второго примера.

1) Вычитаем единицы. Из нуля вычесть четыре нельзя, потому занимаем один десяток. Но единицы в разряде десятков отсутствуют, потому занимаем сотню. Единицы в разряде сотен отсутствуют, потому занимаем тысячу.
Одина тысяча – это десять сотен, можем занять одну сотню. Одна сотня – это десять десятков, теперь занимаем один десяток. Один десяток – это десять единиц. 10 – 4 = 6.
2) Вычисляем десятки. Мы добавили 10 десятков, но один заняли. 9 – 2 = 7 десятков.
3) Вычисляем сотни. Мы добавили 10 сотен, но одну заняли, осталось 9. 9 – 1 = 8 сотен.
4) Вычисляем единицы тысяч. Была 1 тысяча, но ее мы заняли. Осталось ноль, но его мы не пишем.
5) Читаем ответ: 876.
Объясняем вычисление третьего примера.

1) Вычитаем единицы. Из семи вычесть восемь нельзя, потому занимаем один десяток. Но единицы в разряде десятков отсутствуют, потому занимаем сотню. Отсутствуют сотни и отсутствуют единицы тысяч, потому занимаем один десяток тысяч.
Один десяток тысяч – это десять единиц тысяч, можем занять одну тысячу. Одна тысяча – это 10 сотен, можем занять из сотен. Одна сотня – это десять десятков, теперь занимаем один десяток. Один десяток – это десять единиц да ещё 7. 17 – 8 = 9.
2) Вычисляем десятки. Мы добавили 10 десятков, но один заняли. 9 – 4 = 5 десятков.
3) Вычисляем сотни. Мы добавили 10 сотен, но одну заняли, осталось 9. 9 – 6 = 3 сотни.
4) Вычисляем единицы тысяч. Мы добавили 10 единиц тысяч, но одну заняли, осталось 9 единиц тысяч. Переписываем 9, так как единицы тысяч в вычитаемом отсутствуют.
5) Осталось два десятка тысяч, их переписываем.
6) Читаем ответ: 29 359.
Номер 267.
Ответ:
Помни о том, что существует алгоритм письменного вычитания. Многозначные числа необходимо записывать предельно внимательно, чтобы каждый разряд стоял под разрядом. Следуй алгоритму письменного вычитания:
1) Записываю уменьшаемое так, чтобы каждая цифра стояла в своей клетке, ставлю знак минус.
2) Записываю вычитаемое так, чтобы разряд стоял под разрядом.
3) Провожу черту, обозначающую знак равно.
4) Вычитание начинаю с единиц низшего разряда.
5) Вычитаю десятки (и так до максимального разряда).
6) Вычитание окончено. Читаю ответ. Значение разности от вычитания ...
Выполняем вычисления.

Оформляем задание в тетрадь.
Номер 268.
Проверь, верны ли равенства.
Ответ:7 км 080 м = 7 · 1 000 + 80 = 7 080 м.
7 км 080 м ≠ 70 800 м, равенство неверно.
10 т 300 кг = 10 · 1000000 + 300 · 1000 = 10 300 000 г.
10 т 300 кг ≠ 10 300 г, равенство неверно.
3 м2 = 3 · 10 000 = 30 000 см2.
3 м2 ≠ 20 000 см2, равенство неверно.
4 ч = 4 · 60 = 240 мин.
4 ч ≠ 100 мин, равенство неверно.
8 мин 20 с = 8 · 60 + 20 = 500 с.
8 мин 20 с = 500 с, равенство верно.
20 км2 = 20 · 1 000 000 = 20 000 000 м2.
20 км2 = 20 000 000 м2, равенство верно.
Чтобы понять, верны ли равенства, приведи обе части числовых значений единиц измерения длины, времени, площади к одним единицам измерения.
1) Длина – величина, характеризующая протяженность объекта на плоскости, выражается в таких единицах измерения, как миллиметр, сантиметр, дециметр, метр, километр.
Помни о соотношении числовых значений единиц измерения длины:
1 см = 10 мм.
1 дм = 10 см.
1 м = 100 см.
1 м = 10 дм.
1 км = 1000 м.
2) Площадь – величина, которая характеризует размер части плоскости, занятой фигурой. Измеряется в таких единицах измерения, как: мм2, см2, дм2, м2, км2 и др.
Помни о соотношении числовых значений единиц измерения площади:
1 см2 = 100 мм2.
1 дм2 = 100 см2.
1 м2 = 10 000 см2.
1 м2 = 100 дм2.
3) Время – величина, характеризующая продолжительность какого-либо события и отношения его к временной прямой: прошлому, настоящему или будущему. Измеряется в таких единицах измерения, как: 1 секунда, 1 минута, 1 час, 1 сутки, 1 неделя, 1 месяц, 1 год, 1 век.
Помни о соотношении числовых значений единиц измерения времени:
1 мин – 60 сек.
1 час – 60 мин.
1 сут – 24 час.
1 мес – 28, 29, 30 или 31 сут.
1 год – 12 мес.
1 год – 356 сут.
4) Масса – величина, которая характеризует вес предмета, то, сколько он весит. Масса может измеряться в таких единицах измерения, как грамм, килограмм, центнер, тонна.
Помни о соотношении числовых значений единиц измерения времени:
1 кг = 1000 г.
1 ц = 100 кг.
1 т = 1000 кг.
Выполняем вычисления и проверяем верны ли равенства.
7 км 080 м = 70 800 м.
7 км 080 м; 1 км – 1 000 м, значит, 7 · 1 000 = 7 000 км да еще 80 м – 7 080 м.
7 080 м не равно 70 800, значит, равенство неверно.
10 т 300 кг = 10 300 г.
10 т 300 кг; 1 т – 1000000 г, значит, 10 · 1000000 г = 10000000 г да еще 300 г – 10000300 г.
10 000 300 г не равно 10 300 г, значит, равенство неверно.
3 м2 и 20 000 см2.
20 000 см2; 1 м2 – это 10 000 см2, потому что 100 см · 100 см = 10 000 см2, значит, 20 000 : 10 000 = 2 м2.
3 м2 неравны 2 м2, значит, равенство неверно.
4 ч = 100 мин.
4 ч; 1 ч – 60 мин, значит, 4 ч – 60 мин · 4 = 240 мин.
240 мин не равно 100 мин, значит, равенство неверно.
8 мин 20 с = 500 с.
8 мин 20 с; 1 мин – 60 сек., значит, 8 · 60 = 480 сек да еще 20 сек. = 500 сек.
500 сек. = 500 сек., значит, равенство верно.
20 км2 = 20 000 000 м2.
20 000 000 м2; 1 км2 – 1 000 000 м2, потому что 1 000 · 1 000 = 1 000 000 км2, получается, 20 · 1 000 000 = 20 000 000 м2.
20 000 000 м2 = 20 000 000 м2, значит, равенство верно.
Оформляем задание в тетрадь.
7 км 080 м = 7 · 1 000 + 80 = 7 080 м.
7 км 080 м ≠ 70 800 м, равенство неверно.
10 т 300 кг = 10 · 1000000 + 300 · 1000 = 10 000 300 г.
10 т 300 кг ≠ 10 300 г, равенство неверно.
3 м2 = 3 · 10 000 = 30 000 см2.
3 м2 ≠ 20 000 см2, равенство неверно.
4 ч = 4 · 60 = 240 мин.
4 ч ≠ 100 мин, равенство неверно.
8 мин 20 с = 8 · 60 + 20 = 500 с.
8 мин 20 с = 500 с, равенство верно.
20 км2 = 20 · 1 000 000 = 20 000 000 м2.
20 км2 = 20 000 000 м2, равенство верно.
Номер 269.
(Устно.) Заполни пропуски.
Ответ:В 1 тыс. – 10 сотен, в 1 с. – 10 дес., в 1 дес. – 10 ед., в 1 мил. – 10 сот. тыс., в 1 с. тыс. – 10 дес. тыс., в 1 дес. тыс. – 10 тыс.
Помни о том, что одна и та же цифра, стоя на разных позициях в записи числа может обозначать количество единиц разных разрядов.
Помни о том, в каком порядке следуют разряды:
единицы,
десятки,
тысячи,
единицы тысяч,
десятки тысяч,
сотни тысяч.
При необходимости обращайся к таблице, чтобы вспомнить классово-разрядный состав числа.

1 дес. – 10 ед.
1 сот. – 10 дес.
1 тыс. – 10 сот.
1 дес. тыс. – 10 тыс.
1 сот.тыс. – 1 дес. тыс.
1 миллион – 10 сот.тыс.
Помни, что 10 единиц низшего разряда образуют одну единицу высшего.
Устно заполним пропуски в первом столбике.
В 1 тысяче – 10 сотен.
в 1 сотне – 10 десятков.
в 1 десятке – 10 единиц.
Устно заполним пропуски во втором столбике.
в 1 миллионе – 10 сотен тысяч.
в 1 сотне тысяч – 10 десятков тысяч.
в 1 десятке тысяч – 10 тысяч.
Номер 270.
В январе фабрика выпустила 4850 т бумаги, а в феврале – на 365 т меньше. Из всей этой бумаги 6335 т пошло на изготовление общих тетрадей, а из остальной бумаги сделали тонкие тетради. Поставь вопрос и реши задачу.
Ответ:Вопрос: сколько тонн бумаги пошло на изготовление тонких тетрадей? Задачу можно оформить краткой записью или с помощью схемы.


Следу плану при решении задачи:
1) Определи количество бумаги, выпущенной в феврале.
2) Узнай, сколько всего бумаги было выпущено.
3) Узнай, сколько бумаги потратили на производство тонких тетрадей.
Оформляем условие в виде краткой записи или схематического чертежа.

Общие – 6335 т.
Тонкие – ? т.
Рассуждаем.
В январе фабрика выпустила 4 850 тонн бумаги, а в феврале – на 365 тонн меньше. На 365 тонн меньше, значит, что выпущено столько же бумаги, сколько в январе, но без 365 тонн. Получается, чтобы узнать, сколько тонн бумаги было выпущено за февраль, нужно из количества бумаги за январь вычесть 365 тонн бумаги.
1) 4850 – 365 = 4485 (т) – в феврале.
Продолжаем рассуждение.
Общее количество бумаги складывается из количества бумаги. Выпущенной в январе и феврале. Значит, чтобы узнать, сколько бумаги было выпущено всего, складываем количество бумаги в каждый из месяц.
2) 4850 + 4485 = 9335 (т) – всего.
Продолжаем рассуждение.
Из этого количества бумаги 6 335 тонн пошло на изготовление общих тетрадей. Общее количество потраченной бумаги складывается из количества бумаги, потраченной на изготовление общих тетрадей и тонких. Значит, чтобы узнать, сколько тонких тетрадей можно сделать, нужно из общего количества бумаги вычесть количество бумаги, потраченной на общие тетради.
3) 9335 – 6335 = 3000 (т).
Записываем ответ.
Ответ: 3000 т бумаги пошло на тонкие тетради.
Решение выражением: (4850 + (4850 – 365)) – 6 335.
Оформляем задание в тетрадь.


Номер 271.
Садовод разбил фруктовый сад прямоугольной формы. Ширина сада 50 м, а длина в 2 раза больше ширины. Сколько деревьев можно посадить на этой площади, если отводить на одно дерево 10 м2.
Ответ:
1) 50 ∙ 2 = 100 (м) – длина сада.
2) 50 ∙ 100 = 5000 (м2) – площадь сада.
3) 5000 : 10 = 500 (д.) – можно посадить в саду.
Ответ: 500 деревьев всего можно посадить в саду.
Площадь – величина, которая характеризует размер части плоскости, занятой фигурой. Измеряется в таких единицах измерения, как: мм2, см2, дм2, м2, км2 и др.
Помни о соотношении числовых значений единиц измерения площади:
1 см2 = 100 мм2.
1 дм2 = 100 см2.
1 м2 = 10 000 см2.
1 м2 = 100 дм2.
Прямоугольник имеет две величины для вычисления площади: длина и ширина. Вычисляется площадь по формуле: а · в, где а – ширина прямоугольника, а в – длина прямоугольника.
Оформляем условие в виде таблицы.

Рассуждаем.
Ширина сада 50 м, а длина – в 2 раза больше ширины. Значит, что длина такая, как две ширины. Получается, чтобы узнать, сколько метров составляют длину, нужно ширину умножить на 2.
1) 50 ∙ 2 = 100 (м) – длина сада.
Продолжаем рассуждение.
Теперь нам известны обе величины для вычисления площади участка. Подставляем в формулу полученные значения:
S = 50 м · 100 м = 5 000 м2.
2) 50 · 100 = 5000 (м2) – площадь сада.
Продолжаем рассуждение.
Из таблицы видно, что общая площадь участка складывается из площади, расходуемой на каждое дерево. Значит чтобы узнать, сколько деревьев посажено на участке, общую площадь участка необходимо разделить на количество места на одно дерево.
3) 5000 : 10 = 500 (д.) – можно посадить в саду.
Продолжаем рассуждение.
Ответ: 500 деревьев.
Решение выражением: (50 · (50 · 2)) : 10, где 50 · (50 · 2) – площадь участка.
Номер 272.
Найди частное и остаток. Выполни проверку.
Ответ:

Вспомни названия компонентов действия деления и зависимость между компонентами и результатами действия деления:
Делимое : делитель = значение частного.
Значение частного · делитель = делимое.
Делимое : значение частного = делитель.
Рассуждаем.
Чтобы проверить деление с остатком, нужно неполное частное умножить на делитель, к полученному произведению прибавить остаток и в результате вычислений должно получиться делимое. При этом помним, что остаток всегда должен быть меньше делителя.
Выполняем вычисления и оформляем задание в тетрадь.


Номер 273.
В 100 одинаковых вагонах можно перевезти 6000 т угля. В трёх таких вагонах помещается столько угля, сколько в двух большегрузных вагонах. Сколько тонн угля в одном большегрузном вагоне?
Ответ:Эту задачу можно оформить с помощью краткой записи или таблицы: 100 вагонов – 6000 тонн угля. 3 вагона = 2 большегруза. 1 большегруз – ? тонн угля.

1) 6000 : 100 = 60 (т) – угля, в 1-ом вагоне.
2) 60 ∙ 3 = 180 (т) – угля, в 3-х вагонах.
3) 180 : 2 = 90 (т)
Ответ: 90 тонн угля в большегрузном вагоне.
Помни о том, каков конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а · 3, а – первый множитель, а 3 – количество множителей.
Помни о зависимости между компонентами и результатом действия умножения:
1 множитель · 2 множитель = значение произведения.
Значение произведения : 1 множитель = 2 множитель.
Значение произведения : 2 множитель = 1 множитель.
Данная задача: вида «масса 1 вагона, количество вагонов, общая масса груза» характеризуется зависимостями между компонентами:
Масса 1 вагона · количество вагонов = общая масса вагонов.
Общая масса вагонов : количество вагонов = масса 1 вагона.
Общая масса вагонов : масса 1 вагона = количество вагонов.
Оформляем условие в виде краткой записи или таблицы.
Эту задачу можно оформить с помощью краткой записи или таблицы:
100 вагонов – 6000 тонн угля.
3 вагона – 2 большегруза.
1 большегруз – ? тонн угля.

Рассуждаем.
Из таблицы видно, что общее количество груза складывается из количества груза в каждом вагоне. Значит, чтобы узнать, сколько груза помещается в 1 вагоне, нужно общую массу груза разделить на количество вагонов.
1) 6000 : 100 = 60 (т) – угля, в 1-ом вагоне.
Продолжаем рассуждение.
Нам известна масса 1 вагона, количество вагонов, а общее количество груза – нет. При этом, общая масса груза складывается из масса груза в каждом вагоне. Значит, чтобы узнать, сколько груза помещается во всех вагонах, нужно массу 1 вагона умножить на их количество.
2) 60 ∙ 3 = 180 (т) – угля, в 3-х вагонах.
Продолжаем рассуждение.
Из таблицы видно, что общее количество груза складывается из массы груза в каждом вагоне. Значит, чтобы узнать, сколько груза в 1 большегрузе, нужно общую массу груза разделить на количество вагонов.
3) 180 : 2 = 90 (т).
Записываем ответ.
Ответ: 90 тонн угля в большегрузном вагоне.
Решение выражением: ((6 000 : 10) · 3) : 2.
Номер 274.
Ответ:
Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий. Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Следуй плану при устном объяснении вычитания в столбик:
1) Записываю уменьшаемое так, чтобы каждая цифра стояла в своей клетке. Ставлю знак минус;
2) Записываю вычитаемое так, чтобы разряд стоял под разрядом;
3) Провожу черту, обозначающую знак равно;
4) Вычитание начинаю с единиц низшего разряда. Вычитаю единицы;
5) Вычитаю десятки;
6) Вычитаю сотни;
7) Вычитание окончено. Читаю ответ.
Выполняем вычисления по действиям.
10 106 – (8 508 – 3 469) = 5 067

(1 000 + 200) : (20 · 5) = 12
1) 1 000 + 200 = 1 200
2) 20 · 5 = 100
3) 1200 : 100 = 12
Оформляем задание в тетрадь.

Номер 275.
Какая доля каждой фигуры закрашена?

Первая фигура состоит из 12 клеток, а закрашено 6 клеток: 12 : 6 = 2, значит закрашена половина фигуры.
Вторая фигура состоит из 16 клеток, а закрашено 4 клетки: 16 : 4 = 4, значит закрашена четверть фигуры.
Доля – одна часть из тех, на которые разделили целое. Например, если целое разделили на 4 части, то доля – это одна четвертая, т.е. одна часть из четырех.
Одна вторая – половина целого.
Одна третья – третья часть от целого.
Одна четвертая – четвертинка или четвертая часть от целого.
Одна пятая – пятая часть от целого и т.д.
Первое слово в названии долей указывает на количество долей, которые взяли, а второе – на сколько частей разделили целое.
Вид задачи: на нахождение целого по части.
Шаг 1.
Рассуждаем.
Понять, на сколько таких частей можно разбить большую фигуру, разбивая ее, т.е. практическим способом.
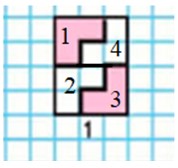
4 одинаковых доли. Закрашено две. 4 : 2 = 2, значит, закрашена ровно половина, т.е. одна вторая.
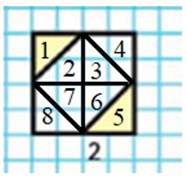
8 одинаковых долей. Закрашено две. 8 : 2 = 4, значит, закрашена ровно четвертая часть, т.е. одна четвертая.
Шаг 2.
Запишем числа в таблицу.
По определению площади.
Площадь – часть плоскости, занятая фигурой. Площадь может измеряться в разных единицах измерения, например, клетках. Тогда, площадь большой фигуры – сумма площадей фигур, из которых она состоит.
Значит, сначала в каждой фигуре вычислю площадь большой фигуры, а затем маленьких частей. Чтобы понять, какую часть они составляют от целого, или, иначе говоря, долю, разделю площадь большой фигуры на площадь маленькой.

S большой фигуры - 12 кл,
S маленьких фигур: 3 кл + 3 кл = 6 кл,
Отношение площадей фигур: 12 кл: 6 кл = 2, значит, маленькие фигуры составляют половину от площади большой фигуры, т.е. одну вторую.

S большой фигуры - 16 кл,
S маленьких фигур: 2 кл + 2 кл = 4 кл,
Отношение площадей фигур: 16 кл : 4 кл = 4, значит, маленькие фигуры составляют четвертую часть от площади большой фигуры, т.е. одну четвертую.
Оформляем задание в тетрадь.
Первая фигура состоит из 12 клеток, а закрашено 6 клеток:
12 : 6 = 2, значит закрашена половина фигуры.
Вторая фигура состоит из 16 клеток, а закрашено 4 клетки:
16 : 4 = 4, значит закрашена четверть фигуры.
Задание внизу страницы.
Ответ:
Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий. Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Следуй плану при устном объяснении вычитания в столбик:
1) Записываю уменьшаемое так, чтобы каждая цифра стояла в своей клетке. Ставлю знак минус;
2) Записываю вычитаемое так, чтобы разряд стоял под разрядом;
3) Провожу черту, обозначающую знак равно;
4) Вычитание начинаю с единиц низшего разряда. Вычитаю единицы;
5) Вычитаю десятки;
6) Вычитаю сотни;
7) Вычитание окончено. Читаю ответ.
а · 10 – увеличить в 10 раз, т.е. умножить на 10, вычисляется умножением.
а : 100 – уменьшить в 100 раз, т.е. разделить на 100, вычисляется делением.
Выполняем вычисления.
31 010 – (5 000 – 3 774) = 29 784

(4 000 – 500 : 100) · 10 = 39 950
1) 500 : 100 = 5
2) 4 000 – 5 = 3 995
3) 3 995 · 10 = 39 950
Оформляем задание в тетрадь.

Объясни вычисления.


Вычитаем единицы. От нуля отнять 6 мы не можем. Занимаем у десятков. В разряде десятков отсутствуют единицы. Занимаем у сотен. Одна сотня – это десять десятков. Теперь один десяток мы можем отдать.
10 – 6 = 4. Записываем под единицами.
Вычитаем десятки. Мы добавили к десяткам одну сотню, то есть десять десятков, но при этом заняли десяток, осталось 9 дес. 9 – 2 = 7 Записываем под десятками.
Вычитаем сотни. Мы заняли одну сотню из шести, поэтому записываем пять сотен.
Читаем ответ: 574.

Вычитаем единицы. Из нуля вычесть четыре нельзя, потому занимаем один десяток. Но единицы в разряде десятков отсутствуют, потому занимаем сотню. Единицы в разряде сотен отсутствуют, потому занимаем тысячу.
Одина тысяча — это десять сотен, можем занять одну сотню. Одна сотня – это десять десятков, теперь занимаем один десяток. Один десяток — это десять единиц. 10 – 4 = 6.
Вычисляем десятки. Мы добавили 10 десятков, но один заняли. 9 – 2 = 7 десятков.
Вычисляем сотни. Мы добавили 10 сотен, но одну заняли, осталось 9. 9 – 1 = 8 сотен.
Вычисляем единицы тысяч. Была 1 тысяча, но ее мы заняли. Осталось ноль, но его мы не пишем.
Читаем ответ: 876.

Вычитаем единицы. Из семи вычесть восемь нельзя, потому занимаем один десяток. Но единицы в разряде десятков отсутствуют, потому занимаем сотню. Отсутствуют сотни и отсутствуют единицы тысяч, потому занимаем один десяток тысяч.
Один десяток тысяч – это десять единиц тысяч, можем занять одну тысячу. Одна тысяча – это 10 сотен, можем занять из сотен. Одна сотня – это десять десятков, теперь занимаем один десяток. Один десяток – это десять единиц да ещё 7. 17 – 8 = 9.
Вычисляем десятки. Мы добавили 10 десятков, но один заняли. 9 – 4 = 5 десятков.
Вычисляем сотни. Мы добавили 10 сотен, но одну заняли, осталось 9. 9 – 6 = 3 сотни.
Вычисляем единицы тысяч. Мы добавили 10 единиц тысяч, но одну заняли, осталось 9 единиц тысяч. Переписываем 9, так как единицы тысяч в вычитаемом отсутствуют.
Осталось два десятка тысяч, их переписываем.
Читаем ответ: 29 359.
Номер 271.
Ответ:
Номер 272.
Проверь, верны ли равенства.
Ответ:7 км 080 м = 7 · 1 000 + 80 = 7 080 м.
7 км 080 м ≠ 70 800 м, равенство неверно.
10 т 300 кг = 10 · 1000000 + 300 · 1000 = 10 300 000 г.
10 т 300 кг ≠ 10 300 г, равенство неверно.
3 м2 = 3 · 10 000 = 30 000 см2.
3 м2 ≠ 20 000 см2, равенство неверно.
4 ч = 4 · 60 = 240 мин
4 ч ≠ 100 мин, равенство неверно.
8 мин 20 с = 8 · 60 + 20 = 500 с.
8 мин 20 с = 500 с, равенство верно.
20 км2 = 20 · 1 000 000 = 20 000 000 м2.
20 км2 = 20 000 000 м2, равенство верно.
Номер 273.
(Устно.) Заполни пропуски.
Ответ:В 1 тыс. – 10 сотен, в 1 с. – 10 дес., в 1 дес. – 10 ед., в 1 мил. – 10 сот. тыс., в 1 с. тыс. – 10 дес. тыс., в 1 дес. тыс. – 10 тыс.
Номер 274.
В январе фабрика выпустила 4850 т бумаги, а в феврале – на 365 т меньше. Из всей этой бумаги 6335 т пошло на изготовление общих тетрадей, а из остальной бумаги сделали тонкие тетради. Задай вопрос и реши задачу.
Ответ:Вопрос: сколько тонн бумаги пошло на изготовление тонких тетрадей? Задачу можно оформить краткой записью или с помощью схемы.


Номер 275.
Садовод разбил фруктовый сад прямоугольной формы. Ширина сада 50 м, а длина в 2 раза больше ширины. Сколько деревьев можно посадить на этой площади, если отводить на одно дерево 10 м2.
Ответ:
1) 50 ∙ 2 = 100 (м) – длина сада.
2) 50 ∙ 100 = 5000 (м2) – площадь сада.
3) 5000 : 10 = 500 (д.) – можно посадить в саду.
Ответ: 500 деревьев всего можно посадить в саду.
Номер 276.
Найди частное и остаток. Выполни проверку.
Ответ:

Номер 277.
В 100 одинаковых вагонах можно перевезти 6000 т угля. В трёх таких вагонах помещается столько угля, сколько в двух большегрузных вагонах. Сколько тонн угля в одном большегрузном вагоне?
Ответ:Эту задачу можно оформить с помощью краткой записи или таблицы: 100 вагонов – 6000 тонн угля. 3 вагона = 2 большегруза. 1 большегруз – ? тонн угля.

1) 6000 : 100 = 60 (т) – угля, в 1-ом вагоне.
2) 60 ∙ 3 = 180 (т) – угля, в 3-х вагонах.
3) 180 : 2 = 90 (т)
Ответ: 90 тонн угля в большегрузном вагоне.
Номер 278.
Ответ:
Номер 279.
Какая доля каждой фигуры закрашена?

Первая фигура состоит из 12 клеток, а закрашено 6 клеток: 12 : 6 = 2, значит закрашена половина фигуры.
Вторая фигура состоит из 16 клеток, а закрашено 4 клетки: 16 : 4 = 4, значит закрашена четверть фигуры.
Задание внизу страницы.
Ответ:
Задание на полях страницы.
Ребус.

394 − 285 = 109
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.