Математика 4 класс учебник Моро, Бантова 1 часть ответы – страница 35

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Номер 12.
Выполни деление с остатком и сделай проверку.
Ответ:
Помним конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а · 3, а – первый множитель, а 3 – количество множителей.
Вспомним зависимость между компонентами и результатом действия умножения, деления:
Делимое : делитель = значение частного.
Делимое : значение частного = делитель.
Значение частного · делитель = делимое.
Выполняем письменное деление.
832 : 9
1) Выделю первое неполное делимое, чтобы определить количество цифр в частном. Первое неполное делимое – 83, значит, в частном будет 2 цифры.
2) Нахожу цифру десятков в частном: 83 дес. : 9 = 9 дес.
3) Нахожу, сколько десятков разделили: 9 дес. · 9 = 81 дес.
4) Нахожу, сколько десятков осталось разделить: 83 дес. – 81 дес. = 2 дес. 2 дес. < 9 ., значит, в частном 9 дес.
5) Образую второе неполное делимое: 2 дес. – это 20 ед. да еще 2 ед. – это 22 единицы.
6) Нахожу количество единиц в частном: 22 ед.: 9 = 2 ед.
7) Нахожу, сколько единиц разделили: 2 ед. · 9 = 18 ед.
8) Нахожу, сколько единиц осталось разделить: 22 ед. – 18 ед. = 4. 4ед. < 9., значит, деление окончено.
9) Читаю ответ: значение частного от деления 832 на 9 равно 92 и остаток 4.
Аналогично выполняем (641 : 3, 587 : 8, 667 : 7).
Выполняем проверку.
Самопроверкой в ходе и результате вычислений является то, что:
1) Мы постоянно сравниваем остаток с делителем. Он всегда должен быть меньше делителя. В противном случае деление выполнении неверно или не завершено;
2) Мы проверяем, правильно ли подобрана цифра того или иного разряда через умножение на делитель. Цифра единиц разряда подобрана верно тогда, когда число от умножения меньше чем неполное делимое.
3) Мы получаем искомое число, выполняя умножения результата деления на делитель и прибавления остатка. Если число и делимое совпали, то деление выполнено верно. В противном случае, была допущена ошибка.
Оформляем задание в тетрадь.

Номер 13.
Ответ:.jpg)
Помним о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Расставляем порядок действий и выполняем вычисления.
(57 · 9 + 87) : 6 = 100

3) 600 : 6 = 100
(648 : 4 – 78) · 4 = 336

(807 – 55 · 6) : 9 = 53

(900 – 755 : 5) : 7 = 107

137 · 6 : 2 = 411

219 : 3 · 8 = 584

Оформляем задание в тетрадь.

Номер 14.
Реши уравнения.
Ответ:
Уравнение – равенство с неизвестной, при подстановке числа в которую, получается верное равенство.
Вспомни названия компонентов действия умножения, и зависимость между компонентами и результатом действия умножения:
1 множитель · 2 множитель = значение произведения.
Значение произведения : 1 множитель = 2 множитель.
Значение произведения : 2 множитель = 1 множитель.
Уменьшаемое – вычитаемое = значение разности.
Уменьшаемое – значение разности = вычитаемое.
Значение разности + вычитаемое = уменьшаемое.
Делимое : делитель = значение разности.
Делимое : значение разности = делитель.
Значение разности · делитель = делимое.
Анализируем.
7 · х = 7, х – неизвестный множитель. Чтобы найти неизвестный множитель, нужно значение произведения разделить на известный множитель.
х – 12 = 0, х – неизвестное уменьшаемое. Чтобы найти неизвестное уменьшаемое, нужно к значению разности прибавить вычитаемое.
32 : х = 1, х – неизвестный делитель. Чтобы найти неизвестный делитель, нужно делимое разделить на значение частного.
83 – х = 0, х – неизвестное вычитаемое. Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть значение разности.
Решаем.

Номер 15.

Реши задачу разными способами.
1) В магазин привезли 5 мешков риса, по 40 кг в каждом, и 5 мешков пшена, по 35 кг в каждом. В первый день продали 120 кг риса и 140 кг пшена. Сколько килограммов крупы осталось продать?
2) Столовая расходовала одну неделю по 70 л молока в день, а другую неделю – по 80 л молока в день. Сколько литров молока израсходовали за эти две недели, если столовая работала 5 дней в неделю? 6 дней?
Задача 1:

1-й способ решения:
1) 40 ∙ 5 = 200 (кг) – риса привезли.
2) 35 ∙ 5 = 175 (кг) – пшена привезли.
3) 200 − 120 = 80 (кг) – риса осталось.
4) 175 − 140 = 35 (кг) – пшена осталось.
5) 80 + 35 = 115 (кг) – крупы осталось продать.
Ответ: 115 кг крупы осталось продать в магазине.
2-й способ решения:
1) 40 ∙ 5 = 200 (кг) – риса привезли в магазин.
2) 35 ∙ 5 = 175 (кг) – пшена привезли в магазин.
3) 200 + 175 = 375 (кг) – крупы привезли всего.
4) 120 + 140 = 260 (кг) – крупы продали.
5) 375 − 260 = 115 (кг) – крупы осталось продать.
Ответ: 115 кг крупы осталось продать в магазине.
Задача 2:

1) 70 ∙ 5 = 350 (л) – молока за неделю израсходовали когда столовая работала 5 дней.
2) 80 ∙ 5 = 400 (л) – молока израсходовали за другую неделю когда столовая работала 5 дней.
3) 350 + 400 = 750 (л) – израсходовали за две недели в пятидневном режиме работы.
Ответ: 750 литров израсходовали за 2 недели работы по 5 дней в неделю.
1) 70 ∙ 6 = 420 (л) – молока использовала столовая за 6 дней работы.
2) 80 ∙ 6 = 480 (л) – молока использовала столовая за следующие 6 дней работы.
3) 420 + 480 = 900 (л) – молока израсходовала столовая за 2 недели работы по 6 дней.
Ответ: 900 литров молока израсходовала столовая за 2 недели работы по 6 дней.
Задача 1:
Помним конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а · 3, а – первый множитель, а 3 – количество множителей.
Помним о зависимости между компонентами и результатом действия умножения:
1 множитель · 2 множитель = значение произведения.
Значение произведения : 1 множитель = 2 множитель.
Значение произведения : 2 множитель = 1 множитель.
Данная задача характеризуется зависимостями между компонентами:
Масса 1 мешка · кол-во мешков = общее кол-во крупы.
Общее кол-во крупы : кол-во мешков = масса 1 мешка.
Общее кол-во крупы : масса 1 мешка = кол-во мешков.
Задача 2:
Помним конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а · 3, а – первый множитель, а 3 – количество множителей.
Помним о зависимости между компонентами и результатом действия умножения:
1 множитель · 2 множитель = значение произведения.
Значение произведения : 1 множитель = 2 множитель.
Значение произведения : 2 множитель = 1 множитель.
Данная задача характеризуется зависимостями между компонентами:
Расход молока в 1 день · количество дней = общее кол-во молока.
Общее кол-во молока : расход молока в 1 день = количество дней.
Общее кол-во молока : количество дней = расход молока в 1 день
Шаг 1.
Оформляем условие в виде таблицы.

Рассуждаем.
Общее количество крупы складывается из количества крупы каждого мешка, при этом количество крупы в каждом мешке одинаковое. Значит, чтобы узнать, сколько крупы привезли, нужно массу 1 мешка умножить на количество мешков.
1) 40 ∙ 5 = 200 (кг) – риса привезли.
2) 35 ∙ 5 = 175 (кг) – пшена привезли.
После того, как мы узнали, сколько крупы привезли всего каждого вида, решение задачи развивается по двум путям, образуя 2 способа решения:
Шаг 3.
Продолжаем рассуждение.
Общее количество крупы складывается из количества проданной крупы и оставшейся. Значит, чтобы узнать, сколько крупы осталось после продажи, нужно из общего количества крупы вычесть количество проданной.
3) 200 – 120 = 80 (кг) – риса осталось.
4) 175 – 140 = 35 (кг) – пшена осталось.
Продолжаем рассуждение.
Общее количество оставшейся в магазине крупы складывается из количества оставшегося пшена и риса. Значит, чтобы узнать, сколько крупы осталось, нужно сложить количество оставшегося риса и пшена.
5) 80 + 35 = 115 (кг) – крупы осталось продать.
Записываем ответ.
Ответ: 115 кг крупы.
Шаг 3.
Продолжаем рассуждение.
Общее количество привезенной крупы складывается из количества привезенного риса и пшена. Значит, чтобы узнать, сколько всего было привезено крупы, нужно сложить количество привезенного пшена и риса.
3) 200 + 175 = 375 (кг) – крупы привезли всего.
Продолжаем рассуждение.
Общее количество проданной крупы складывается из количества проданного риса и пшена. Значит, чтобы узнать, сколько крупы было продано, нужно сложить количество проданного риса и пшена.
4) 120 + 140 = 260 (кг) – крупы продали.
Продолжаем рассуждение.
Общее количество привезенной крупы складывается из количества оставшейся крупы и проданной. Значит, чтобы узнать, сколько крупы осталось в магазине, нужно из общего количества крупы вычесть количество проданной.
5) 375 – 260 = 115 (кг) – крупы осталось продать.
Записываем ответ.
Ответ: 115 кг крупы.
Подзадача 1.
Шаг 1.
Оформляем условие в виде таблицы.

Шаг 2.
Рассуждаем.
Общее количество молока затраченное столовой складывается из количества молока, расходуемого в каждый из дней, при этом количество молока, расходуемого в каждый из дней одинаково. Значит, чтобы узнать, сколько молока расходовала столовая в каждую неделю, нужно количество молока, расходуемого в каждый из дней умножаю на количество дней.
1) 5 ∙ 70 = 350 (л) – молока за неделю израсходовали, когда столовая работала 5 дней.
2) 5 ∙ 80 = 400 (л) – молока израсходовали за другую неделю, когда столовая работала 5 дней.
Продолжаем рассуждение.
Общее количество расходуемого молока складывается из количества молока расходуемого столовой в первую и вторую неделю. Значит, чтобы узнать, сколько всего молока расходуется за 5 дней столовой в две недели, нужно сложить количества расходуемого молока столовой в каждую неделю.
3) 350 + 400 = 750 (л) – израсходовали за две недели в пятидневном режиме работы.
Шаг 2.
Рассуждаем.
Общее количество расходуемого в 1 день молока складывается из количества расходуемого молока каждой недели. Значит, чтобы узнать, сколько молока расходуется в 1 день столовой каждой недели, нужно сложить количество молока, расходуемого в 1 день на каждой неделе.
1)70 + 80 = 150 (л) – общий расход молока в 1 день каждой недели.
Продолжаем рассуждение.
Общее количество расходуемого молока складывается из количества расходуемого молока в каждый из дней. Значит, чтобы узнать, сколько молока было израсходовано за 5 дней работы нужно общий расход молока в 1 день умножить на количество дней, ведь расход молока в 1 день одинаковый.
2) 150 · 5 = 750 (л) – молока расходуется всего за 2 недели.
Записываем ответ.
Ответ: 750 литров израсходовали за 2 недели работы по 5 дней.
Шаг 1.
Оформляем условие в виде таблицы.

Шаг 2.
Рассуждаем.
Общее количество молока, затраченное столовой складывается из количества молока, расходуемого в каждый из дней, при этом количество молока, расходуемого в каждый из дней одинаково. Значит, чтобы узнать, сколько молока расходовала столовая в каждую неделю, нужно количество молока, расходуемого в каждый из дней умножаю на количество дней.
1) 70 · 6 = 420 f молока за неделю израсходовали, когда столовая работала 6 дней.
2) 80 · 6 = 480 (л) f молока израсходовали за другую неделю, когда столовая работала 6 дней.
Продолжаем рассуждение.
Общее количество расходуемого молока складывается из количества молока расходуемого столовой в первую и вторую неделю. Значит, чтобы узнать, сколько всего молока расходуется за 6 дней столовой в две недели, нужно сложить количества расходуемого молока столовой в каждую неделю.
3) 420 + 480 = 900 (л) – израсходовали за две недели в шестидневном режиме работы.
Шаг 2.
Рассуждаем.
Общее количество расходуемого в 1 день молока складывается из количества расходуемого молока каждой недели. Значит, чтобы узнать, сколько молока расходуется в 1 день столовой каждой недели, нужно сложить количество молока, расходуемого в 1 день на каждой неделе. 1) 70 + 80 = 150 (л) – общий расход молока в 1 день каждой недели.
Продолжаем рассуждение.
Общее количество расходуемого молока складывается из количества расходуемого молока в каждый из дней. Значит, чтобы узнать, сколько молока было израсходовано за 6 дней работы нужно общий расход молока в 1 день умножить на количество дней, ведь расход молока в 1 день одинаковый.
2) 150 · 6 = 900 (л) – молока расходуется всего за 2 недели.
Записываем ответ.
Ответ: 900 литров израсходовали за 2 недели работы по 6 дней в неделю.
Реши задачу разными способами.
1) В магазин привезли 5 контейнеров мандаринов, по 40 кг в каждом, и 5 контейнеров с виноградом, по 35 кг в каждом. В первый день продали 120 кг мандаринов и 140 кг винограда. Сколько всего килограммов мандаринов и винограда осталось продать?
2) Столовая расходовала одну неделю по 70 л молока в день, а другую неделю – по 80 л молока в день. Сколько литров молока израсходовали за эти две недели, если столовая работала 5 дней в неделю? 6 дней?
Задача 1:
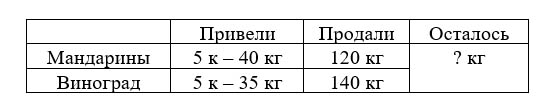
1-й способ решения:
1) 40 ∙ 5 = 200 (кг) – мандаринов привезли.
2) 35 ∙ 5 = 175 (кг) – винограда привезли.
3) 200 – 120 = 80 (кг) – мандаринов осталось.
4) 175 – 140 = 35 (кг) – винограда осталось.
5) 80 + 35 = 115 (кг) – мандаринов и винограда осталось продать.
Ответ: 115 кг мандаринов и винограда осталось продать в магазине.
1) 40 ∙ 5 = 200 (кг) – мандаринов привезли в магазин.
2) 35 ∙ 5 = 175 (кг) – винограда привезли в магазин.
3) 200 + 175 = 375 (кг) – мандаринов и винограда привезли всего.
4) 120 + 140 = 260 (кг) – мандаринов и винограда продали.
5) 375 – 260 = 115 (кг) – мандаринов и винограда осталось продать.
Ответ: 115 кг мандаринов и винограда осталось продать в магазине.
Задача 2:

1) 70 ∙ 5 = 350 (л) – молока за неделю израсходовали когда столовая работала 5 дней.
2) 80 ∙ 5 = 400 (л) – молока израсходовали за другую неделю когда столовая работала 5 дней.
3) 350 + 400 = 750 (л) – израсходовали за две недели в пятидневном режиме работы.
Ответ: 750 литров израсходовали за 2 недели работы по 5 дней в неделю.
1) 70 ∙ 6 = 420 (л) – молока использовала столовая за 6 дней работы.
2) 80 ∙ 6 = 480 (л) – молока использовала столовая за следующие 6 дней работы.
3) 420 + 480 = 900 (л) – молока израсходовала столовая за 2 недели работы по 6 дней.
Ответ: 900 литров молока израсходовала столовая за 2 недели работы по 6 дней.
Номер 16.
Ответ:
Помним о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Помним алгоритм умножения трехзначного числа на однозначное:
1) Записываю первый множитель так, чтобы каждая цифра стояла в своей клетке. Ставлю знак умножить;
2) Записываю второй множитель так, чтобы разряд сто
ял под разрядом;
3) Провожу черту, обозначающую знак равно;
4) Умножение начинаю с единиц низшего разряда;
5) Умножаю десятки;
6) Умножаю сотни;
7) Умножение окончено. Читаю ответ.
Следуйте плану при устном объяснении вычитания в столбик:
1) Записываю уменьшаемое так, чтобы каждая цифра стояла в своей клетке. Ставлю знак минус;
2) Записываю вычитаемое так, чтобы разряд стоял под разрядом;
3) Провожу черту, обозначающую знак равно;
4) Вычитание начинаю с единиц низшего разряда. Вычитаю единицы;
5) Вычитаю десятки;
6) Вычитаю сотни;
7) Вычитание окончено. Читаю ответ.
Выполняем письменное умножение.

Расставляем порядок действий и выполняем вычисления.
307 · 3 – 704 : 8 = 833

65 · 8 – 535 : 5 = 413

684 : 9 + (506 – 102 · 3) = 276

4) 76 + 200 = 276
736 : 4 + (607 – 428 : 4) = 684

2) 607 – 107 = 500
4) 184 + 500 = 684
Оформляем задание в тетрадь.

Номер 17.
Ответ:
Помним о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Вычисление значений выражения сводится к применению правил:
Правило прибавления числа к сумме:
(а + в) + с = (а + с) + в.
Правило прибавления суммы к числу:
а + (в + с) = (а + в) + с.
Правило вычитания суммы из числа:
а – (в + с) = (а – в) – с.
Правило вычитания числа из суммы:
(а + в) – с = (а – с) + в.
Расставляем порядок действий и выполняем вычисления.
230 + 70 · 3 = 440
1) 70 · 3 = 210
2) 230 + 210 = 230 + (200 + 10) = (230 + 200) + 10 = 430 + 10 = 440, по правилу прибавления суммы к числу.
(460 + 40) · 2 = 1000
1) 460 + 40 = (400 + 60) + 40 = 400 + (60 + 40) = 400 + 100 = 500, по правилу прибавления числа к сумме.
2) 500 · 2 = 1000
(470 – 70) · 2 = 800
1) 470 – 70 = (400 + 70) – 70 = 400 + (70 – 70) = 400 + 0 = 400, по правилу вычитания числа из суммы.
2) 400 · 2 = 800
380 – 80 · 3 = 140
1) 80 · 3 = 240
2) 380 – 240 = 380 – (200 + 40) = (380 – 200) – 40 = 180 – 40 = 140, по правилу вычитания суммы из числа.
600 + 180 : 6 + 9 = 639
1) 180 : 6 = 30
2) 600 + 30 = 630
3) 630 + 9 = (600 + 30) + 9 = 600 + (30 + 9) = 600 + 39 = 639, по правилу прибавления числа к сумме.
360 : (120 + 240) · 4 = 4
1) 120 + 240 = 120 + (200 + 40) = (120 + 200) + 40 = 320 + 40 = 360, по правилу прибавления суммы к числу.
2) 360 : 360 = 1
3) 1 · 4 = 4
Оформляем задание в тетрадь.

Номер 1.
Сколько разрядов содержится в каждом классе? Как называются разряды и классы?
Ответ:Три разряда. Разряды – единицы, десятки, сотни. Классы – единиц, тысяч, миллионов, миллиардов.
Помним о том, что одна и та же цифра, стоя на разных позициях в записи числа может обозначать количество единиц разных разрядов.
Помни о том, в каком порядке следуют разряды:
единицы,
десятки,
тысячи,
единицы тысяч,
десятки тысяч,
сотни тысяч.
Вспоминаем.
1 класс – единицы: разряд единиц, разряд десятков, разряд сотен. 2 класс – тысячи: разряд единиц тысяч, десятков тысяч, сотен тысяч. 3 класс – миллионом: разряд единиц миллионов, десятков миллионов, сотен миллионов.
Отвечаем на вопросы.
Три разряда.
Разряды – единицы, десятки, сотни.
Классы – единиц, тысяч, миллионов, миллиардов
Номер 2.
Покажи на примере, что 10 единиц любого разряда образуют единицу следующего разряда.
Ответ:10 ∙ 10 = 100 100 ∙ 10 = 1000
Помним о том, в каком порядке следуют разряды:
единицы,
десятки,
тысячи,
единицы тысяч,
десятки тысяч,
сотни тысяч.
При необходимости обращайтесь к таблице, чтобы вспомнить классово-разрядный состав числа.

Помним, что 10 единиц низшего разряда образуют одну единицу высшего.
10 ед. = 1 дес., потому что 1 · 10 = 10
10 дес. = 1 сот, потому что 10 · 10 = 100 и т.д.
Номер 3.
Покажи на примере, что 1000 единиц одного класса образуют единицу следующего класса.
Ответ:1 ∙ 1000 = 1000 10 ∙ 1000 = 10000
Помним о том, в каком порядке следуют разряды:
единицы,
десятки,
тысячи,
единицы тысяч,
десятки тысяч,
сотни тысяч.
При необходимости обращайтесь к таблице, чтобы вспомнить классово-разрядный состав числа.

Помним, что 1000 единиц низшего класса образуют одну единицу высшего класса.
1000 ед. – 1 тыс., потому что 1 · 1 000 = 1 000
1000 дес. = 1 дес. тыс., потому что 10 · 1 000 = 10 000 и др.
Номер 4.
Сколько цифр используется для записи чисел? Назови их. Покажи, как можно одними и теми же цифрами записать разные числа.
Ответ:10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 127, 271, 172, 721 ...
Вспомните, сколько существует цифр. Перечислите их и подумайте, можно ли составить числа, используя не только эти цифры.
Вспоминаем.
Сколько бы цифр не было в числе, из какого бы количества знаков оно не состояло, и на каком бы месте цифры не стояли, всегда в записи чисел будет использовано 10 возможных цифр, которые существуют:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Приводим пример.
Возьмём цифры: 1, 2 и 7.
Получаем: 127, 271, 172, 721 ...
Номер 5.
Покажи на примере, как изменяется значение цифры при изменении её места в записи числа.
Ответ:247 – 7 единиц 274 – 7 десятков 724 – 7 сотен
Помним о том, что одна и та же цифра, стоя на разных позициях в записи числа может обозначать количество единиц разных разрядов.
Помним о том, в каком порядке следуют разряды:
единицы,
десятки,
тысячи,
единицы тысяч,
десятки тысяч,
сотни тысяч.
При необходимости обращайся к таблице, чтобы вспомнить классово-разрядный состав числа.

Анализируем.
Внесу числа 247, 274 и 724 в таблицу, чтобы увидеть, как изменяется роль цифры 7 в записи числа:

Делаем вывод.
247 – 7 единиц.
274 – 7 десятков.
724 – 7 сотен.
Номер 6.
Как получить число, которое больше данного в 10 раз? в 100 раз? в 1000 раз?
Ответ:Умножить на 10 (в 10 раз больше), умножить на 100 (в 100 раз больше), Умножить на 1000 (в 1000 раз больше).
Умножить число на 10, значит, увеличить его в 10 раз, т.е. приписать к записи числа один ноль.
Умножить на 100, значит, увеличить его в 100 раз, т.е. приписать к записи числа два нуля.
Умножить на 1000, значит, увеличить его в 1000 раз, т.е. приписать к записи числа три нуля.
Пояснение.
Умножить на 10 (в 10 раз больше);
Умножить на 100 (в 100 раз больше);
Умножить на 1000 (в 1000 раз больше).
Номер 7.
Объясни, как можно сравнить числа.
Ответ:Числа сравниваются по классам и по разрядам. Например: сравним 351 и 349 Разряд сотен у чисел равны. Сравниваем разряд десятков 5 > 4, поэтому 351 > 349.
Помним о том, как сравнивают многозначные числа:
1) Сравнить, сколько знаков в числах. В большем числе количество знаков больше.
2) В случае, если количество знаков одинаковое, сравнивай количество единиц каждого разряда, начиная с высшего. Сравниваю количество сотен тысяч.
3) Если количество сотен тысяч одинаковое, сравниваю количество десятков тысяч.
4) Если количество десятков тысяч одинаковое, сравниваю единицы тысяч. Аналогично с разрядами класса единиц.
5) Делаю вывод о том, какое число больше.
Ответим на вопрос.
Числа сравниваются по классам и по разрядам.
Приведём пример.
900 001 и 901 000
1) Оба числа шестизначные, значит, начинаю сравнение с единиц высшего разряда.
2) Высший разряд – сотни тысяч. Количество сотен тысяч в обоих числах одинаковое.
3) Сравниваю количество десятков тысяч. Количество одинаковое – 9 дес. тыс.
4) Количество единиц тысяч в первом числе – 0, а во втором – 1. 0 < 1, значит, первое число меньше второго числа.
Тогда, 900 001 < 901 000
5 312 000 и 5 320 000
1) Оба числа семизначные, значит, начинаю сравнение с единиц высшего разряда.
2) Высший разряд – единицы миллионов. Количество единиц этого разряда в числах одинаковых.
3) Сравниваю количество сотен тысяч. Количество одинаковое – 3 сотни тысяч.
4) Количество десятков тысяч в первом числе – 1, а во втором – 2. 1 < 2, значит, первое число меньше второго числа.
Тогда, 5 312 000 < 5 320 000
Задание на полях страницы.
Цепочка.

14 ∙ 8 = 112 112 : 2 = 56 56 : 4 = 14 14 ∙ 5 = 70
Выполним действия по порядку. Первый желтый треугольник – число, с которого начинать действие. Помним конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а · 3, а – первый множитель, а 3 – количество множителей.
Выполняем цепочку вычислений, где ответ предыдущего действия является первым из компонентов следующего действия.
14 · 8 = 112, это по 14 – 8 раз, где 14 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
112 : 2 = 56, потому что 56 · 2 = 112, это по 56 – 2 раза, где 56 – одинаковое слагаемое, а 2 – количество одинаковых слагаемых.
56 : 4 = 14, потому что 14 · 4 = 56, это по 14 – 4 раза, где 14 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.
14 · 5 = 70, это по 14 – 5 раз, где 14 – одинаковое слагаемое, а 5 – количество одинаковых слагаемых.
Оформляем задание в тетрадь.
14 ∙ 8 = 112
112 : 2 = 56
56 : 4 = 14
14 ∙ 5 = 70
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.