Математика 3 класс учебник Моро, Волкова 2 часть ответы – страница 33

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2021-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Что узнали. Чему научились
Номер 1.
Выполни деление с остатком.
Ответ:7 : 6 = 1 (ост. 1) 30 : 8 = 3 (ост. 6)
7 : 8 = 0 (ост. 7) 40 : 7 = 5 (ост. 5)
41 : 7 = 5 (ост. 6) 46 : 9 = 5 (ост. 1)
65 : 9 = 7 (ост. 2) 46 : 8 = 5 (ост. 6)
39 : 10 = 3 (ост. 9)
48 : 10 = 4 (ост. 8)
1) Повтори, как выполняется деление с остатком.
2) Повтори случаи вне табличного деления.
3) Вспомни, что остаток всегда меньше делителя.
Вычисляем.
7 : 6 = 1 (ост. 1)
7 не делится на 6 без остатка. Вспомним, какое самое большое число до 7 делится на 6 без остатка. Это 6.
Найдём частное: 6 : 6 = 1.
Найдём остаток: 7 – 6 = 1.
7 : 8 = 0 (ост. 7)
Надо 7 разделить на 8.
Так как 7 < 8, то целых частей нет, а остаток 7.
30 : 8 = 3 (ост. 6)
30 не делится на 8 без остатка. Вспомним, какое самое большое число до 30 делится на 8 без остатка. Это 24.
Найдём частное: 24 : 8 = 3.
Найдём остаток: 30 – 24 = 6.
40 : 7 = 5 (ост. 5)
40 не делится на 7 без остатка. Вспомним, какое самое большое число до 40 делится на 7 без остатка. Это 35.
Найдём частное: 35 : 7 = 5.
Найдём остаток: 40 – 35 = 5.
41 : 7 = 5 (ост. 6)
41 не делится на 7 без остатка. Вспомним, какое самое большое число до 41 делится на 7 без остатка. Это 35.
Найдём частное: 35 : 7 = 5.
Найдём остаток: 41 – 35 = 6.
65 : 9 = 7 (ост. 2)
65 не делится на 9 без остатка. Вспомним, какое самое большое число до 65 делится на 9 без остатка. Это 63.
Найдём частное: 63 : 9 = 7.
Найдём остаток: 65 – 63 = 2.
46 : 9 = 5 (ост. 1)
46 не делится на 9 без остатка. Вспомним, какое самое большое число до 46 делится на 9 без остатка. Это 45.
Найдём частное: 45 : 9 = 5.
Найдём остаток: 46 – 45 = 1.
46 : 8 = 5 (ост. 6)
46 не делится на 8 без остатка. Вспомним, какое самое большое число до 46 делится на 8 без остатка. Это 40.
Найдём частное: 40 : 8 = 5.
Найдём остаток: 46 – 40 = 6.
39 : 10 = 3 (ост. 9)
39 не делится на 10 без остатка. Вспомним, какое самое большое число до 39 делится на 10 без остатка. Это 30.
Найдём частное: 30 : 10 = 3 дес. : 1 дес. = 3.
Найдём остаток: 39 – 30 = 9.
48 : 10 = 4 (ост. 8)
48 не делится на 10 без остатка. Вспомним, какое самое большое число до 48 делится на 10 без остатка. Это 40.
Найдём частное: 40 : 10 = 4 дес. : 1 дес. = 4.
Найдём остаток: 48 – 10 = 8.
Выполняем проверку.
7 : 6 = 1 (ост. 1)
1) 6 ∙ 1 = 6 – неполное делимое
2) 6 + 1 = 7 – делимое
7 = 7
3) 1 < 6 – остаток должен быть меньше делителя.
7 : 8 = 0 (ост. 7)
1) 0 ∙ 8 = 0 – неполное делимое
2) 0 + 7 = 7 – делимое
7 = 7
3) 7 < 8 – остаток должен быть меньше делителя.
30 : 8 = 3 (ост. 6)
1) 8 ∙ 3 = 24 – неполное делимое
2) 24 + 6 = 30 – делимое
30 = 30
3) 6 < 8 – остаток должен быть меньше делителя.
40 : 7 = 5 (ост. 5)
1) 7 ∙ 5 = 35 – неполное делимое
2) 35 + 5 = 40 – делимое
40 = 40
3) 5 < 7 – остаток должен быть меньше делителя.
41 : 7 = 5 (ост. 6)
1) 7 ∙ 5 = 35 – неполное делимое
2) 35 + 6 = 41 – делимое
41 = 41
3) 6 < 7 – остаток должен быть меньше делителя.
65 : 9 = 7 (ост. 2)
1) 9 ∙ 7 = 63 – неполное делимое
2) 63 + 2 = 65 – делимое
65 = 65
3) 2 < 9 – остаток должен быть меньше делителя.
46 : 9 = 5 (ост. 1)
1) 9 ∙ 5 = 45 – неполное делимое
2) 45 + 1 = 46 – делимое
46 = 46
3) 1 < 9 – остаток должен быть меньше делителя.
46 : 8 = 5 (ост. 6)
1) 8 ∙ 5 = 40 – неполное делимое
2) 40 + 6 = 46 – делимое
46 = 46
3) 6 < 8 – остаток должен быть меньше делителя.
39 : 10 = 3 (ост. 9)
1) 10 ∙ 3 = 30 – неполное делимое
2) 30 + 9 = 39 – делимое
39 = 39
3) 9 < 10 – остаток должен быть меньше делителя.
48 : 10 = 4 (ост. 8)
1) 10 ∙ 4 = 40 – неполное делимое
2) 40 + 8 = 48 – делимое
48 = 4
3) 8 < 10 – остаток должен быть меньше делителя.
Оформляем задание в тетрадь.
7 : 6 = 1 (ост. 1)
7 : 8 = 0 (ост. 7)
30 : 8 = 3 (ост. 6)
40 : 7 = 5 (ост. 5)
41 : 7 = 5 (ост. 6)
65 : 9 = 7 (ост. 2)
46 : 9 = 5 (ост. 1)
46 : 8 = 5 (ост. 6)
39 : 10 = 3 (ост. 9)
48 : 10 = 4 (ост. 8)
Номер 2.
1) Какие остатки могут получиться при делении на 2? на 4? на 9? на 15? 2) Может ли при делении на 6 получиться в остатке 5? 6? 7?
Ответ:1) При делении на 2 может получиться остаток 1.
При делении на 4 могут получиться остатки: 1, 2, 3.
При делении на 9 могут получиться остатки: 1, 2, 3, 4, 5, 6, 7, 8.
При делении на 15 могут получиться остатки: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14.
2) При делении на 6 числа 6 и 7 в остатке получиться не могут, так как остаток должен
быть меньше делителя.
Вспомни, что остаток всегда меньше делителя.
Рассуждаем.
Задание 1.
Так как остаток всегда меньше делителя, значит.
При делении на 2 остаток: 0, 1.
При делении на 4 остаток: 0, 1, 2, 3.
При делении на 9 остаток: 0, 1, 2, 3, 4, 5, 6, 7, 8.
При делении на 15 остаток: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14.
Продолжаем рассуждение.
Задание 2.
При делении на 6 может получиться остаток 5.
При делении на 6 не может получится остаток 6 и 7, так как остаток должен быть меньше делителя, а 6 = 6 и 7 > 6.
Номер 3.
1) Делитель 10, частное 3. Найди делимое. 2) Частное чисел 72 и 8 уменьши на 3.
Ответ:1) х : 10 = 3 х = 10 ∙ 3 х = 30 2) 72 : 8 – 3 = 6
1) «уменьшить на 3» – значит, из числа нужно вычесть 3.
2) Вспомни о зависимости между компонентами и результатами действий деления.
Рассуждаем.
Представим выражение в виде уравнения.
х : 10 = 3
Вычисляем.
Чтобы найти неизвестное делимое, нужно значение частного умножить на делитель.
х : 10 = 3
х = 10 ∙ 3
х = 30
Ответ: 30.
Рассуждаем.
Составим выражение.
72 : 8 – 3 – частное чисел 72 и 8 уменьшили на 3.
Вычисляем.
72 : 8 – 3 = 9 – 3 = 6
1) 72 : 8 = 9
2) 9 – 3 = 6
Номер 4.
Запиши по 3 числа, при делении которых на 7 в остатке получится 5; 3.
Ответ:19 : 7 = 2 (ост. 5)
26 : 7 = 3 (ост. 5)
47 : 7 = 6 (ост. 5)
10 : 7 = 1 (ост. 3)
17 : 7 = 2 (ост. 3)
24 : 7 = 3 (ост. 3)
1) Повтори, как выполняется деление с остатком.
2) Вспомни, что остаток всегда меньше делителя.
Рассуждаем.
Чтобы найти все делимые при делении которых на 7 в остатке получится 5, начни с числа 5 и потом каждый раз к делимому прибавляй число 7.
Чтобы найти все делимые при делении которых на 7 в остатке получится 3, начни с числа 3 и потом каждый раз к делимому прибавляй число 7.
Оформляем задание в тетрадь.
Выбери по 3 примера из каждого.
В остатке по 5:
5 : 7 = 0 (ост. 5)
12 : 7 = 1 (ост. 5)
19 : 7 = 2 (ост. 5)
26 : 7 = 3 (ост. 5)
33 : 7 = 4 (ост. 5)
40 : 7 = 5 (ост. 5)
47 : 7 = 6 (ост. 5)
54 : 7 = 7 (ост. 5)
61 : 7 = 8 (ост. 5)
68 : 7 = 9 (ост. 5)
75 : 7 = 10 (ост. 5)
В остатке 3:
3 : 7 = 0 (ост. 3)
10 : 7 = 1 (ост. 3)
17 : 7 = 2 (ост. 3)
24 : 7 = 3 (ост. 3)
31 : 7 = 4 (ост. 4)
38 : 7 = 5 (ост. 3)
45 : 7 = 6 (ост. 3)
52 : 7 = 7 (ост. 3)
59 : 7 = 8 (ост. 3)
66 : 7 = 9 (ост. 3)
73 : 7 = 10 (ост. 3)
Номер 5.
Надо упаковать 86 кубиков в коробки, по 10 штук в каждую. Сколько потребуется таких коробок? Сколько кубиков останется?
Ответ:Было – 86 к. Упаковали – ? к. по 10 куб. Осталось – ? куб. 86 : 10 = 8 (ост. 6) – понадобится 8 коробок, останется 6 кубиков. Ответ: 8 коробок понадобится для упаковки 86 кубиков да ещё 6 кубиков останется.
1) Повтори, как выполняется деление с остатком.
2) Вспомни, что остаток всегда меньше делителя.
Оформляем условие в виде краткой записи.

Рассуждаем.
Всего 86 кубиков и в каждой коробке по 10 кубиков. Чтобы узнать сколько потребуется коробок нужно общее количество кубиков разделить на количество кубиков в 1 коробке.
86 : 10 = 8 (ост. 6) – понадобится.
Если разделить 86 кубиков на группы по 10 кубиков, то получим 8 такие группы и ещё останется 6 кубиков.
Значит, нужно 8 коробок и 6 кубиков останется.
Записываем ответ.
Ответ: 8 коробок, 6 кубиков останется.
Номер 6.
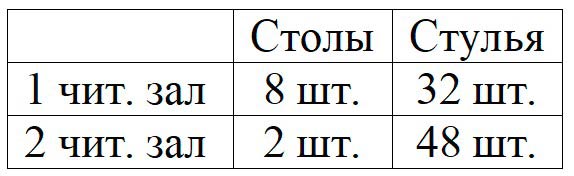
В библиотеке в одном читальном зале поставили 8 новых столов и 32 новых стула, а в другом зале поставили 2 новых стола и 48 новых стульев. Составь по этому условию различные выражения и объясни значение каждого из них.
Ответ:
1) 32 + 48 = 80 – количество стульев в двух залах. 2) 8 + 2 = 10 – количество столов в двух залах. 3) (48 + 32) + (8 + 2) = 90 – сколько всего поставили стульев и столов. 4) 48 – 32 = 16 – на сколько больше стульев поставили во втором зале. 5) 8 – 2 = 6 – на сколько больше столов поставили в первом зале. 6) 32 : 8 = 4 – во сколько раз больше стульев, чем столов поставили в первом зале. 7) 48 : 2 = 24 – во сколько раз больше стульев, чем столов поставили во втором зале. 8) 8 : 2 = 4 – во сколько раз больше столов поставили в первом зале, чем во втором. 9) (48 + 32) – (8 + 2) = 70 – на сколько больше поставили стульев, чем столов.
Используй знаки арифметический действий и скобки, чтобы составить выражения по задаче.
Оформляем условие в виде таблицы.
Рассуждаем.
1) Если сложим количество стульев в первом и втором зале, то получим общее количество стульев.
32 + 48 = 80 (ст.)
2) Если сложим количество столов в первом и втором зале, то получим общее количество столов.
8 + 2 = 10 (ст.)
3) Если из количества столов в первом зале вычтем количество столов во втором зале, то узнаем на сколько больше столов поставили в первом зале.
8 − 2 = 6 (ст.)
4) Если из количества стульев во втором зале вычтем количество стульев в первом зале, то узнаем на сколько больше стульев поставили во втором зале.
48 − 32 = 16 (ст.)
5) Если количество столов в первом зале разделить на количество столов во втором зале, то узнаем во сколько раз столов в первом зале больше, чем во втором зале.
8 : 2 = 4 (раза)
6) Если количество стульев разделить на количество столов в первом зале, то узнаем во сколько раз стульев больше, чем столов в первом зале.
32 : 8 = 4 (раза)
7) Если количество стульев разделить на количество столов во втором зале, то узнаем во сколько раз стульев больше, чем столов во втором зале.
48 : 2 = 24 (раз)
8) Если общее количество столов сложим с общим количеством стульев, то узнаем сколько всего поставили мебели в двух залах.
(48 + 32) + (8 + 2) = 80 + 10 = 90 (шт.)
9) Если из общего количества стульев вычесть общее количество столов, то узнаем на сколько больше поставили стульев, чем столов в двух залах.
(48 + 32) − (8 + 2) = 80 − 10 = 70 (шт.)
10) Если общее количество стульев разделить на общее количество столов, то узнаем во сколько раз больше стульев, чем столов в двух залах.
(48 + 32) : (8 + 2) = 80 : 10 = 8 (раз)
Оформляем задание в тетрадь.
1) 32 + 48 = 80 (ст.) – всего стульев в двух залах.
2) 8 + 2 = 10 (ст.) – всего столов в двух залах.
3) 8 - 2 = 6 (ст.) – на сколько больше столов поставили в первом зале, чем во втором.
4) 48 - 32 = 16 (ст.) – на сколько больше стульев поставили во втором зале, чем в первом.
5) 8 : 2 = 4 (раза) – во сколько раз больше столов поставили в первом зале, чем во втором.
6) 32 : 8 = 4 (раза) – во сколько раз больше стульев, чем столов поставили в первом зале.
7) 48 : 2 = 24 (раз) – во сколько раз больше стульев, чем столов поставили во втором зале.
8) (48 + 32) + (8 + 2) = 80 + 10 = 90 (шт.) – сколько всего поставили стульев и столов в двух залах.
9) (48 + 32) — (8 + 2) = 80 – 10 = 70 (шт.) – на сколько больше поставили стульев, чем столов в двух залах.
10) (48 + 32) : (8 + 2) = 80 : 10 = 8 (раз) – во сколько раз больше стульев, чем столов в двух залах.
Номер 7.
Ответ:

1) Чтобы разделить сумму на число можно разделить на число каждое слагаемое и полученные результаты сложить.
2) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
3) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
4) Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Расставляем порядок действий и выполняем вычисления.
При вычислении выражений используем правило деления суммы на число.
99 : 3 = (90 + 9) : 3 = 90 : 3 + 9 : 3 = 30 + 3 = 33
Представим число 99 в виде суммы чисел 90 и 9, каждое слагаемое разделим на 3 и полученные значения сложим.
75 : 5 = (50 + 25) : 5 = 50 : 5 + 25 : 5 = 10 + 5 = 15
Разложим число 75 на сумму чисел 50 и 25, каждое слагаемое разделим на 5 и полученные результаты сложим.
Выполним вычисления по действиям.
1 2
56 : 7 · 9 = 72
1) 56 : 7 = 8
2) 8 ∙ 9 = 72
1 2
54 : 9 ∙ 6 = 36
1) 54 : 9 = 6
2) 6 ∙ 6 = 36
1 2
36 : 2 + 72 = 90
1) 36 : 2 = (20 + 16) : 2 = 10 + 8 = 18
2) 18 + 72 = 90
1 2
48 : 3 + 14 = 30
1) 48 : 3 = (30 + 18) : 3 = 30 : 3 + 18 : 3 = 10 + 6 = 16
2) 16 + 14 = 30
1 2
(86 − 30) : 8 = 7
1) 86 – 30 = 56
2) 56 : 8 = 7
1 2
(78 – 50) : 7 = 4
1) 78 – 50 = 28
2) 28 : 7 = 4
Оформляем задание в тетрадь.
99 : 3 = (90 + 9) : 3 = 90 : 3 + 9 : 3 = 30 + 3 = 33
75 : 5 = (50 + 25) : 5 = 50 : 5 + 25 : 5 = 10 + 5 = 15
1 2
56 : 7 · 9 = 8 · 9 = 72
1 2
54 : 9 ∙ 6 = 6 · 6 = 36
1 2
36 : 2 + 72 = 18 + 72 = 90
1 2
48 : 3 + 14 = 16 + 14 = 30
1 2
(86 − 30) : 8 = 56 : 8 = 7
1 2
(78 – 50) : 7 = 28 : 7 = 4
Номер 8.
1) Начерти такие четырехугольники и дополни каждый из них до прямоугольника. 2) Найди площади полученных прямоугольников. 3) Найди периметры этих прямоугольников.

1)

S1 = 4 ∙ 2 = 8 см2.
S2 = 5 ∙ 2 = 10 см2.
3)
Р1 = (4 + 2) ∙ 2 = 12 см.
Р2 = (5 + 2) ∙ 2 = 14 см.
1) Периметр прямоугольника – это сумма длин всех его сторон.
2) Площадь прямоугольника равна произведению его длины и ширины.
Рассуждаем.
Рассмотрим фигуры и дорисуем их до прямоугольников.
Фигура 1 (розовая). Чтобы достроить первую фигуру до прямоугольника нужно верхнюю сторону увеличить на 1 см.
.jpg)
Фигура 2 (зеленая). Чтобы достроить фигуру 2 до прямоугольника, нужно верхнюю сторону продолжить влево на 1 см, а вправо на 2 см.
.jpg)
Продолжаем рассуждение.
Измерим стороны полученных прямоугольников.
Розовый прямоугольник. Длина равна 4 см, ширина – 2 см.
Зеленый прямоугольник. Длина равна 5 см, ширина – 2 см.
Вычисляем.
Вычислим площадь прямоугольников.
Чтобы вычислить площадь прямоугольника нужно длину умножить на ширину.
4 см ∙ 2 см = 8 см2 – площадь розового прямоугольника.
5 см ∙ 2 см = 10 см2 – площадь зеленого прямоугольника.
Вычислим периметр прямоугольника.
Чтобы вычислить периметр прямоугольника нужно сумму ширины и длины умножить на 2.
4 см ∙ 2 + 2 см ∙ 2 = (4 см + 2 см) ∙ 2 = 6 см ∙ 2 = 12 см – периметр розового прямоугольника.
5 см ∙ 2 + 2 см ∙ 2 = (5 см + 2 см) ∙ 2 = 7 см ∙ 2 = 14 см – периметр зеленого прямоугольника.
Оформляем задание в тетрадь.
.jpg)
2)
4 см ∙ 2 см = 8 – площадь розового прямоугольника.
5 см ∙ 2 см = 10 – площадь зеленого прямоугольника.
3)
(4 см + 2 см) ∙ 2 = 6 см ∙ 2 = 12 см – периметр розового прямоугольника.
(5 см + 2 см) ∙ 2 = 7 см ∙ 2 = 14 см – периметр зеленого прямоугольника.
Задание на полях страницы
Набери множителями:

4 ∙ 2 ∙ 6 = 48 6 ∙ 2 ∙ 4 = 48 3 ∙ 8 ∙ 2 = 48 4 ∙ 3 ∙ 4 = 48
Подбери такие комбинации чисел, чтобы при умножении получалось 38. Для этого перебирай разные числа, чтобы найти верное решение, которых существует множество.
Устные рассуждения.
Умножая данные числа нужно набрать число 38.
Множители можно менять местами.
Записываем решение в тетрадь.
Найдём возможные варианты, в которых произведение чисел будет равно 38.
Выбери один из вариантов:
2 ∙ 4 ∙ 6 = 8 ∙ 6 = 48
3 ∙ 4 ∙ 4 = 3 ∙ 16 = 48
2 ∙ 3 ∙ 8 = 6 ∙ 8 = 48
6 ∙ 8 = 48
Номер 15.
Найди на рисунке прямые, острые и тупые углы. Выпиши их номера.

Прямые углы: 8, 9, 10, 11, 13, 14, 12, 15. Острые углы: 1, 2, 3, 4, 6. Тупые углы: 5, 7.
1) Чтобы узнать название угла, сравнивай каждый угол с прямым углом.
2) Тупой угол – больше 90º;
3) Прямой угол – равен 90º;
4) Острый угол – меньше 90º.
Рассуждаем.
.jpg)
Рассмотрим углы.
1 – меньше прямого, значит острый;
2 – меньше прямого, значит острый;
3 – меньше прямого, значит острый;
4 – меньше прямого, значит острый;
5 – больше прямого, значит тупой;
6 – меньше прямого, значит острый;
7 – больше прямого, значит тупой;
8 – прямой угол;
9 – прямой угол;
10 – прямой угол;
11 – прямой угол;
12 – прямой угол;
13 – прямой угол;
14 – прямой угол;
15 – прямой угол;
Делаем вывод.
Прямые углы: 8, 9, 10, 11, 12, 13, 14, 15.
Острые углы: 1, 2, 3, 4, 6.
Тупые углы: 5, 7.
Номер 16.
Выполни деление с остатком.
Ответ:36 : 7 = 5 (ост. 1) 44 : 5 = 8 (ост. 4) 60 : 8 = 7 (ост. 4) 80 : 12 = 6 (ост. 8) 44 : 18 = 2 (ост. 8)
1) Повтори, как выполняется деление с остатком.
2) Вспомни, что остаток всегда меньше делителя.
Рассуждаем.
36 : 7 = 5 (ост. 1)
36 не делится на 7 без остатка. Вспомним, какое самое большое число до 36 делится на 7 без остатка. Это 35.
Найдём частное: 35 : 7 = 5.
Найдём остаток: 36 – 35 = 1.
44 : 5 = 8 (ост. 4)
44 не делится на 5 без остатка. Вспомним, какое самое большое число до 44 делится на 5 без остатка. Это 40.
Найдём частное: 40 : 5 = 8.
Найдём остаток: 44 – 40 = 4.
60 : 8 = 7 (ост. 4)
60 не делится на 8 без остатка. Вспомним, какое самое большое число до 60 делится на 8 без остатка. Это 56.
Найдём частное: 56 : 8 = 7.
Найдём остаток: 60 – 56 = 4.
80 : 12 = 6 (ост. 8)
Надо 80 разделить на 12.
Пробуем в частном 6.
Проверим: 12 ∙ 6 = (10 + 2) ∙ 6 = 60 + 12 = 72.
Найдем остаток и сравним его с делителем:
80 – 72 = 8, 8 < 12, значит, частное 6, а остаток 8.
44 : 18 = 2 (ост. 8)
Надо 44 разделить на 18.
Пробуем в частном 2.
Проверим: 18 ∙ 2 = (10 + 8) ∙ 2 = 20 + 16 = 36.
Найдём остаток и сравним его с делителем: 44 – 36 = 8, 8 < 18, значит частное 2, а остаток 8.
Оформляем задание в тетрадь.
36 : 7 = 5 (ост. 1)
44 : 5 = 8 (ост. 4)
60 : 8 = 7 (ост. 4)
80 : 12 = 6 (ост. 8)
44 : 18 = 2 (ост. 8)
Номер 17.
Запиши по 3 числа, при делении которых на 8 в остатке получается 5; 6; 2; 0.
Ответ:29 : 8 = 3 (ост. 5)
45 : 8 = 5 (ост. 5)
61 : 8 = 7 (ост. 5)
22 : 8 = 2 (ост. 6)
38 : 8 = 4 (ост. 6)
54 : 8 = 6 (ост. 6)
18 : 8 = 2 (ост. 2)
58 : 8 = 7 (ост. 2)
82 : 8 = 10 (ост. 2)
16 : 8 = 2 (ост. 0)
64 : 8 = 8 (ост. 0)
72 : 8 = 9 (ост. 0)
1) Повтори, как выполняется деление с остатком.
2) Вспомни, что остаток всегда меньше делителя.
Рассуждаем.
Воспользуемся таблицей умножения на 8.
Чтобы найти число, которое при делении на 8 в остатке было 5, нужно к числу, которое без остатка делится на 8 прибавить 5.
29 : 8 = 24 : 8 + 5 = 3 (ост. 5)
45 : 8 = 40 : 8 + 5 = 5 (ост. 5)
61 : 8 = 56 : 8 + 5 = 7 (ост. 5)
Чтобы найти число, которое при делении на 8 в остатке было 6, нужно к числу, которое без остатка делится на 8 прибавить 6.
22 : 8 = 16 : 8 + 6 = 2 (ост. 6)
38 : 8 = 32 : 8 + 6 = 4 (ост. 6)
54 : 8 = 48 : 8 + 6 = 6 (ост. 6)
Чтобы найти число, которое при делении на 8 в остатке было 2, нужно к числу, которое без остатка делится на 8 прибавить 2.
18 : 8 = 16 : 8 + 2 = 2 (ост. 2)
58 : 8 = 56 : 8 + 2 = 7 (ост. 2)
82 : 8 = 80 : 8 + 2 = 10 (ост. 2)
Если в остатке 0, значит число делится без остатка.
16 : 8 = 16 : 8 + 0 = 2 (ост. 0)
64 : 8 = 64 : 8 + 0 = 8 (ост. 0)
72 : 8 = 72 : 8 + 0 = 9 (ост. 0)
Оформляем задание в тетрадь.
29 : 8 = 3 (ост. 5)
45 : 8 = 5 (ост. 5)
61 : 8 = 7 (ост. 5)
22 : 8 = 2 (ост. 6)
38 : 8 = 4 (ост. 6)
54 : 8 = 6 (ост. 6)
18 : 8 = 2 (ост. 2)
58 : 8 = 7 (ост. 2)
82 : 8 = 10 (ост. 2)
16 : 8 = 2 (ост. 0)
64 : 8 = 8 (ост. 0)
72 : 8 = 9 (ост. 0)
Номер 18.
Выйдет ли квадратная проволочная рамка со стороной 7 см из треугольной рамки, каждая сторона которой равна 9 см?
Квадратная проволочная рамка со стороной 7 см.
Треугольная проволочная рамка со стороной 9 см.
Р(тр) = 9 + 9 + 9
Р(тр) = 27 см.
Периметр проволочного квадратной рамки со стороной 7 см. – 7 · 4
7 · 4 = 28 см., а 27 < 28, по этому проволоки от треугольной рамки не хватит.
Ответ: квадратная проволока не выйдет из треугольной проволоки, потому что проволоки не хватит.
1) Треугольник – это фигура, у которой 3 стороны;
2) Квадрат – это фигура, у которой 4 стороны.
Рассуждаем.
Длина ломанной – это сумма длин всех его отрезков, то есть периметр. Чтобы найти периметр треугольника, нужно все его три стороны сложить. Но у данного треугольника все стороны равны, значит, сложение одинаковых слагаемых можно заменить умножением.
9 ∙ 3 = 27 (см) — периметр треугольника или длина проволоки.
Продолжаем рассуждение.
Чтобы найти периметр квадрата, нужно все его 4 стороны сложить. У квадрата все стороны равны, значит, сложение одинаковых слагаемых можно заменить умножением.
7 ∙ 4 = 28 (см) — периметр квадрата.
Продолжаем рассуждение.
По условию задачи необходимо узнать, выйдет ли квадратная проволочная рамка из треугольной рамки. Для этого необходимо сравнить периметры треугольника и квадрата.
27 см < 28 см, то есть периметр треугольника меньше периметра квадрата.
Можно сделать вывод, что проволоки от треугольной рамки не хватит.
Записываем ответ.
Ответ: квадратная проволочная рамка не выйдет из треугольной рамки.
Номер 19.
На юношеских соревнованиях по плаванию на 100 м Косте осталось проплыть четвертую часть дистанции, а Вите – пятую ее часть. Кто из них ближе к финишу и на сколько метров?
Ответ:1) 100 : 4 = 25 (м) – осталось проплыть Косте.
2) 100 : 5 = 20 (м) – осталось проплыть Вите.
3) 25 – 20 = 5 (м) – на столько ближе Витя.
Ответ: Витя ближе Кости к финишу на 5 м.
1) Доля – одна часть из тех, на которые разделили целое.
2) Первое слово в названии долей указывает на количество долей, которые взяли, а второе – на сколько частей разделили целое.
Оформляем краткую запись.
Костя – 4-я часть осталась.
Витя – 5-я часть осталась.
Дистанция – 100 м.
Кто ближе к финишу и на сколько?
Рассуждаем.
Косте осталось проплыть четвертую часть дистанции.
Одна четвертая часть обозначает, что целое число разделили на 4 части и взяли одну такую часть. Чтобы узнать, сколько Косте осталось проплыть, нужно полную длину дистанции разделить на 4.
100 : 4 = (80 + 20) : 4 = 20 + 5 = 25 (м) – осталось проплыть Косте.
Продолжаем рассуждение.
Витя осталось проплыть пятую часть дистанции.
Одна пятая часть обозначает, что целое число разделили на 5 частей и взяли одну такую часть. Чтобы узнать, сколько Вите осталось проплыть, нужно полную длину дистанции разделить на 5.
100 : 5 = 10 дес. : 5 = 2 дес. = 20 (м) – осталось проплыть Вите.
Продолжаем рассуждение.
Сравниваем показатели. У кого меньше показатель, значит тому меньше плыть до финиша, значит он ближе к финишу.
25 м > 20 м – значит, Витя ближе к финишу, чем Костя.
Чтобы узнать, на сколько Витя ближе к финишу, чем Костя, нужно из расстояния, которое осталось проплыть Косте, вычесть расстояние, которое осталось проплыть Вите.
25 – 20 = 5 (м) – на столько ближе Витя, чем Костя к финишу.
Записываем ответ.
Ответ: на 5 м Витя ближе к финишу, чем Костя.
Номер 20.
Ответ:7 м 8 дм = 78 дм, потому что 78 дм = 78 дм 95 см > 8 дм 9 см, потому что 95 см > 89 см 6 дм 5 см < 7 дм, потому что 65 см < 70 см 18 мм = 1 см 8 мм, потому что 18 мм = 18 мм
Помни, что сравнивать числовые значения длины можно только, если они выражены в одних единицах измерения:
1 см = 10 мм
1 дм = 10 см
Рассуждаем.
Сравним 7 м 8 дм и 78 дм
Переведём 7 м 8 дм в дециметры:
7 м 8 дм = 7 ∙ 10 дм + 8 дм = 78 дм
Так как 78 дм = 78 дм, значит,
7 м 8 дм = 78 дм
Сравним 6 дм 5 см и 7 дм
Переведём 6 дм 5 см и 7 дм в сантиметры:
6 дм 5 см = 6 ∙ 10 см + 5 см = 60 см + 5 см = 65 см
7 дм = 7 ∙ 10 см = 70 см
Так как 65 см < 70 см, значит,
6 дм 5 см < 7 дм
Сравним 95 см и 8 дм 9 см
Переведём 8 дм 9 см в сантиметры:
8 дм 9 см = 8 ∙ 10 см + 9 см = 89 см
Так как 95 см > 89 см, значит,
95 см > 8 дм 9 см
Сравним 18 мм и 1 см 8 мм
Переведём 1 см 8 мм в миллиметры:
1 см 8 мм = 1 ∙ 10 мм + 8 мм = 18 мм
Так как 18 мм = 18 мм, значит,
18 мм = 1 см 8 мм
Запишем решение в тетрадь.
7 м 8 дм = 78 дм
6 дм 5 см < 7 дм
95 см > 8 дм 9 см
18 мм = 1 см 8 мм
Номер 21.
Что больше и на сколько:
Ответ:1) 45 : 9 < 42 : 6 8 ∙ 8 > 9 ∙ 7
42 : 6 – 45 : 9 = 2 8 ∙ 8 – 9 ∙ 7 = 1
2) 18 : 2 > 27 : 9 56 : 7 > 24 : 6
18 : 2 – 27 : 9 = 6 56 : 7 – 24 : 6 = 4
1) Прежде, чем сравнить выражения, вычисли их значения в левой и правой части.
2) Помни о том, что сравнивать численных значения длины можно только, если они выражены в одних единицах измерения.
Рассмотрим выражения.
Сравним 45 : 9 и 42 : 6
Вычислим левую часть: 45 : 9 = 5
Вычислим правую часть: 42 : 6 = 7
Сравним 5 < 7
Вычислим на сколько больше: 7 – 5 = 2
Значит, 45 : 9 < 42 : 6 на 2
Сравним 8 ∙ 8 и 9 ∙ 7
Вычислим левую часть: 8 ∙ 8 = 64
Вычислим правую часть: 9 ∙ 7 = 63
Сравним 64 > 63
Вычислим на сколько больше: 64 – 63 = 1
Значит, 8 ∙ 8 > 9 ∙ 7 на 1.
Сравним 18 : 2 и 27 : 9
Вычислим левую часть: 18 : 2 = 9.
Вычислим правую часть: 27 : 9 = 3.
Сравним 9 > 3
Вычислим на сколько больше: 9 – 3 = 6
Значит, 18 : 2 > 27 : 9 на 6.
Сравним 56 : 7 и 24 : 6
Вычислим левую часть: 56 : 7 = 8
Вычислим правую часть: 24 : 6 = 4
Сравним 8 > 4
Вычислим на сколько больше: 8 – 4 = 4
Значит, 56 : 7 > 24 : 6 на 4.
Запишем решение в тетрадь.
1)
45 : 9 < 42 : 6
45 : 9 = 5
42 : 6 = 7
7 – 5 = 2
45 : 9 < 42 : 6 на 2
8 ∙ 8 > 9 ∙ 7
8 ∙ 8 = 64
9 ∙ 7 = 63
64 – 63 = 1
18 : 2 > 27 : 9 на 6
2)
18 : 2 > 27 : 9
18 : 2 = 9
27 : 9 = 3
9 – 3 = 6
8 ∙ 8 > 9 ∙ 7 на 1
56 : 7 > 24 : 6
56 : 7 = 8
24 : 6 = 4
8 – 4 = 4
56 : 7 > 24 : 6 на 4
Номер 22.
Ответ:
99 : 9 + 32 : 2 = 11 + 16 = 27 96 : 8 + 75 : 5 = 12 + 15 = 27
1) Вспомни, как выполняется деление методом подбора.
2) Чтобы разделить сумму на число, можно разделить на число каждое слагаемое и полученные результаты сложить.
Рассуждаем.
72 : 4 = (40 + 32) : 4 = 40 : 4 + 32 : 4 = 10 + 8 = 18
Представим число 72 в виде суммы 40 и 32, каждое слагаемое разделим на 4 и полученные результаты сложим.
96 : 3 = (90 + 6) : 3 = 90 : 3 + 6 : 3 = 30 + 2 = 32
Представим число 96 в виде суммы 90 и 6, каждое слагаемое разделим на 3 и полученные результаты сложим.
51 : 17 = ?
Нужно 51 разделить на 17.
Пробуем в частном 2 и проверяем:
17 ∙ 2 = 34, 34 < 51, число 2 не подходит.
Пробуем в частном 3 и проверяем:
17 ∙ 3 = 51, 51 = 51, число 3 подходит.
Значит, 51 : 17 = 3.
54 : 18 = ?
Нужно 54 разделить на 18.
Пробуем в частном 2 и проверяем:
18 ∙ 3 = 36, 36 < 54, число 2 не подходит.
Пробуем в частном 3 и проверяем:
18 ∙ 3 = (10 + 8) ∙ 3 = 30 + 24 = 54, 54 = 54, число 3 подходит.
Значит, 54 : 18 = 3.
98 : 14 = ?
Нужно 98 разделить на 14.
Пробуем в частном 6 и проверяем:
14 ∙ 6 = (10 + 4) ∙ 6 = 60 + 24 = 84, 84 < 98, число 6 не подходит.
Пробуем в частном 7 и проверяем:
14 ∙ 7 = (10 + 4) ∙ 7 = 70 + 28 = 98, 98 = 98, число 7 подходит.
Значит, 98 : 14 = 7.
84 : 12 = 7
Нужно 84 разделить на 12.
Пробуем в частном 6 и проверяем:
12 ∙ 6 = 72, 72 < 84, число 6 не подходит.
Пробуем в частном 7 и проверяем:
12 ∙ 7 = 84, 84 = 84, число 7 подходит.
Значит, 84 : 12 = 7.
99 : 9 + 32 : 2 = 27
1) 99 : 9 = 11
2) 32 : 2 = (20 + 12) : 2 = 20 : 2 + 12 : 2 = 10 + 6 = 16
3) 11 + 16 = 27
96 : 8 + 75 : 5 = 27
1) 96 : 8 = (80 + 16) : 8 = 80 : 8 + 16 : 8 = 10 + 2 = 12
2) 75 : 5 = (50 + 25) : 5 = 50 : 5 + 25 : 5 = 10 + 5 = 15
3) 12 + 15 = 27
Запишем решение в тетрадь.
72 : 4 = (40 + 32) : 4 = 10 + 8 = 18
96 : 3 = (90 + 6) : 3 = 30 + 2 = 32
51 : 17 = 3
54 : 18 = 3
98 : 14 = 7
84 : 12 = 7
99 : 9 + 32 : 2 = 11 + 16 = 27
96 : 8 + 75 : 5 = 12 + 15 = 27
Номер 23.
1) Ломаная состоит из четырех одинаковых звеньев, длиной 3 см каждое. Найди длину этой ломаной. 2) Начерти ломаную такой же длины, но состоящую из трех звеньев одной длины; разной длины.
Ответ:1) 4 ∙ 3 = 12 (см) – длина ломаной. Ответ: 12 см длина ломаной.

2)

1) Ломаная линия – геометрическая фигура, состоящая из звеньев-отрезков, не лежащих на одной прямой.
2) Длина ломаной – сумма длин всех его отрезков.
Рассуждаем.
Чтобы найти длину ломаной линии, нужно измерить длину каждого звена-отрезка и сложить все длины. Но длина каждого отрезка одинаковая, значит, сумму одинаковых слагаемых можно заменить умножением.
3 см ∙ 4 = 12 см – длина ломанной.
Записываем ответ.
Ответ: 12 см длина ломаной.
Рассуждаем.
Общая длина ломанной равна 12 см, и она разделена на 3 одинаковые звена. Значит, чтобы найти длину одного звена, нужно общую длину ломанной разделить на количество звеньев.
12 см : 3 = 4 см – длина каждого звена одной длины.
Также нужно начертить ломаную, длина которой 12 см, состоящую из трёх звеньев, которые имеют разную длину.
Например, 12 см = 4 см + 7 см + 1 см
Начертим.
Начертим такие ломанные.
.jpg)
Номер 24.
Начерти в тетради пятиугольник, в котором будет 2 прямых угла, 2 тупых и 1 острый угол.
Ответ:
Вспомни виды углов.
Рассуждаем.
Вспомним виды углов:
Прямой угол – это угол 90 (90 градусов).
Острый угол – это угол, который меньше прямого угла, меньше 90.
Тупой угол – это угол, который больше прямого угла, больше 90.
Начертим такую фигуру.
Нужно начертить фигуру, в которой есть 2 прямых угла, 2 тупых угла и 1 острый угол.
.jpg)
Номер 25.
Как можно сделать равенство верным, не заменяя цифры на карточках? Запиши верное равенство.

Нужно переставить карточки местами. 96 : 4 = 24
Внимательно рассмотри карточки и составь верные равенства (примеры).
Рассуждаем.
Рассмотрим выражение.
.jpg)
Если внимательно посмотреть, то поменяв карточки местами, можно получить верное равенство.
Если карточку 9 поставить перед карточкой 6, а карточку 4 (в числе 64) поставить вместо карточки 2, которую нужно поставить перед карточкой 4 (в числе 49), то получится следующее равенство:
96 : 4 = 24
Выполним проверку.
96 : 4 = (80 + 16) : 4 = 20 + 4 = 24
Представим число 96 в виде суммы 80 и 16, разделим каждое слагаемое на 4 и полученные значения сложим.
Оформляем задание в тетрадь.
96 : 4 = 24.
Номер 26.
1) Найди площадь данной фигуры. Сколькими способами это можно выполнить? Укажи самый простой из них. 2) Начерти такую фигуру и проведи в ней ось симметрии.

1-й способ решения: Длина одной стороны – 1 см Длина второй стороны – 2 см

1) 1 см ∙ 2 см = 2 см2 – площадь одного прямоугольника 2) 2 см2 ∙ 3 = 6 см2 – площадь всей фигуры. Ответ: площадь всей фигуры составляет 6 см2.
2) Ось симметрии.

2-й способ решения: Разделим данную фигуру на 6 одинаковых квадратов. Сторона каждого квадрата равна 1 см.

1) 1 см ∙ 1 см = 1 см2 – площадь одного квадрата 2) 1 см2 ∙ 6 = 6 см2 – площадь всей фигуры. Ответ: площадь всей фигуры составляет 6 см2.
2) Ось симметрии.

3-й способ решения: Дочертим фигуру до квадрата, найдем его площадь и вычтем площадь лишних фигур.

Длина большого квадрата – 3 см.
Длина маленького квадрата – 1 см.
1) 3 см ∙ 3 см = 9 см2 – площадь большого квадрата
2) 1 см ∙ 1 см = 1 см2 – площадь 1 маленького квадрата
3) 1 см2 ∙ 3 = 3 см2 – площадь 3 маленьких квадратов
4) 9 см2 – 3 см2 = 6 см2 – площадь данной фигуры
Ответ: площадь всей фигуры составляет 6 см2.
Первый способ решения самый простой.
2) Ось симметрии.

1) Чтобы вычислить площадь фигуры, нужно понять, какую часть плоскости она занимает в единицах квадратных единицах измерения.
2) Но у фигур сложных, т.е. у которых площадь нельзя вычислить по формуле, нужно поступать иначе. У сложных фигур площадь фигуры равна сумме площадей фигур, из которых она состоит.
Вычисляем.
Вычислим площадь фигуры.
Это можно выполнить тремя способами.
Способ решения 1.
Разделим фигуру на 3 равных прямоугольника.
Получится 3 равных прямоугольника со сторонами 1 см и 2 см.
-(2024).jpg)
Чтобы найти площадь одного прямоугольника нужно длину умножить на ширину.
1) 1 см ∙ 2 см = 2 см2 – площадь одного прямоугольника.
Площадь каждого прямоугольника одинаковы, значит, чтобы найти площадь всех 3 прямоугольников, нужно площадь одного такого прямоугольника умножить на количество прямоугольников.
2) 2 см2 ∙ 3 = 6 см2 – площадь всей фигуры.
Ответ: 6 см2.
Способ решения 2.
Разделим данную фигуру на 6 одинаковых квадратов. Сторона каждого квадрата равна 1 см.
-(2024).jpg)
Чтобы вычислить площадь квадрата, нужно длину умножить на ширину.
1) 1 см ∙ 1 см = 1 см2 – площадь одного квадрата.
Площадь квадратов равны, значит, чтобы найти площадь всех 6 квадратов, нужно площадь одного такого квадрата умножить на количество квадратов.
2) 1 см2 ∙ 6 = 6 см2 – площадь всей фигуры.
Ответ: 6 см2.
Способ решения 3.
Дочертим фигуру до квадрата, найдем его площадь и вычтем площадь лишних фигур (трёх маленьких квадратов).
Длина большого квадрата – 3 см, длина маленького квадрата – 1 см.
-(2024).jpg)
Найдём площадь большого квадрата, умножив длину на ширину.
1) 3 см ∙ 3 см = 9 см2 – площадь большого квадрата.
Найдём площадь маленького квадрата, умножив длину на ширину.
2) 1 см ∙ 1 см = 1 см2 – площадь 1 маленького квадрата.
Найдём площадь 3 маленьких квадратов, умножив площадь одного такого квадрата на 3.
3) 1 см2 ∙ 3 = 3 см2 – площадь 3 маленьких квадратов.
Найдём площадь фигуры, для этого из большого квадрата вычтем площадь 3 маленьких квадратов.
4) 9 см2 – 3 см2 = 6 см2 – площадь данной фигуры.
Ответ: 6 см2.
Выполним задание.
Начертим такую фигуру и найдём ось симметрии.
Ось симметрии – линия, по которой можно сложить фигуру так, что части совпадут при перегибании, т.е. наложении.
У фигуры одна ось симметрии (чёрная линия).
-(2024).jpg)
Если фигуру сложить по синей линии, то правая часть совпадёт с левой её частью.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.